Vladi S. Travkin, 
 Natalya N. Bolotina
Natalya N. Bolotina 
The Annals of Frontier and Exploratory Science
Vladi S. Travkin, 
 Natalya N. Bolotina
Natalya N. Bolotina 

 Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany,
Denver, CO, USA
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany,
Denver, CO, USA

 University of Applied Sciences, Rheinbach, Germany
University of Applied Sciences, Rheinbach, Germany
up to Saturday, 27-Apr-2024 08:49:05 GMT
It might help with the understanding of our approach to the more strict mathematically and physically description of many biological subjects, those mostly are of Heterogeneous, Scaled, and Hierarchical nature well, made by NATURE itself.
To look through, browse our previous analytical reports in other areas where the Heterogeneous, multiphase, scaled media and phenomena are in the core of subject matter, should help in estimation -
Travkin, V.S. and Bolotina, N.N., "Principles, Biological and Mathematical Modeling For Elasticity, Poroelasticity of Soft Biomedia, Polymers with Fluids Mechanics in the Bioporous Two-scale Media," "http://travkin-hspt.com/biophysics/pdf/61BEl-BioHtElasticity-5.1HSPT-f.pdf"
Travkin, V.S. and Bolotina, N.N., "Quantum Chemistry, Physical Chemistry, Molecular Dynamics Simulation, DFT (Density Functional Theory), and Coarse-Graining Techniques Applied in Structural, Cellular Biology, Polymer Science and Implication for Scaleportation," Journal of Alternative Energy and Ecology, No. 2, pp. 58-75, (2011a)
Travkin, V.S. and Bolotina, N.N., "Pseudo-Scaled and Scaled Description and Scaleportation of Inorganic and Organic Polymer and Polymer Composites Properties," Journal of Alternative Energy and Ecology, No. 1, pp. 62-77, (2011b)
The same procedures we have been applying for analyzing the situation, trends and tools that are used in Theoretical Biology, Systems Biology, Cellular Biology, Tissue Engineering and in any other field in Biology and Biosciences that need an implementation of Heterogeneous, Scaled, Hierarchical theoretical tools, concepts, physical and mathematical modeling and simulation along the experimental studies. Both paths are inseparable while questioning the nature of living matters.
We used to select few of the upper quality and broad on subject and its consequencies articles, reports that have also the good conceptual, physical and mathematical basis to discuss under our subject angle.
So far, as usual, in almost all the contemporary physics fields, but Fluid
Mechanics and part of Thermal physics, the tools and math used for
Heterogeneous, Scaled, Hierarchical description are of the 40-60 years old,
from the particle physics, statistical mechanics, and quantum mechanics while
their spatial scales are of

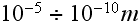 and less range.
and less range.
All these tools are of the One Scale for All (OSFA) methodology, crafted for the sub-atomic as well as intergalactic and of in between scales phenomena with the same mathematics and homogeneous physics we found, when in the math are used the governing equations that have been derived with the homogeneous Gauss-Ostrogradsky theorem.
Which is incorrect.
We have written on that many times through the last like 25-30 years. Well, an education in this direction had stalled at the mark of paradigms of ~ 70s and even earlier of the XX century.
This situation on stagnation was noticed by people in physics, for us conveniently refer to Lee Smolin's -
What does monopoly in technologies, politics, the same it does and to science.
Nevertheless, up to this time (2007-2011) we have selected few papers that represent a much bigger pool of samples. The references in the selected papers might give needed examples of contemporary literature in few areas of biology pretending on ability to name themselves the Quantitative biological methods.
We start with the subject at first referring visitors to our -
where some history of issues is presented.
We allow here to give some rather long quotes only because of the educational purposes. Those who are interested - most of the students and young professionals, not a hard core ones who spent long years applying old paradigms of the one scale-one Universe-one model for all, will be served better with the longer citation taken, then while a short one being understood only by a profound knowledge holder.
The great review paper by Liao, S., Chan, C.K., and Ramakrishna, S., "Biomimetic Nanocomposites for Tissue Engineering," J. Bionanoscience, Vol. 1, No. 1, pp. 1-13(13), (2007);
tells us a lot with regard of how experimentalists understand the matter of scaled, hierarchical organization of human (and not only human) tissue?
From the Abstract:
"Natural extracellular matrix (ECM) consists of various protein fibrils and fibers interwoven within a hydrated network of glycosaminoglycan chains. Such architecture can be the basis for biomimetic biomaterials design."
"It is increasingly clear that the function of tissues is determined by their hierarchical architecture. Understanding of such natural hierarchical nanofibril structures can lead to new design and fabrication concepts for use in tissue engineering. The ability to create hierarchical synthetic nanocomposites .......... creates the potential to engineer better tissue construct for repair and "
Citing from p.4: "Thus, an ideal scaffold would be one that is able to mimic the native ECM in the living system, from its chemical composition to its three-dimensional nanometer scale architecture. These two characteristics are essential because they play an important role in controlling cell behavior... ",
" However, these traditional biomaterials are nonliving, homogenous structures with limited functional capabilities. Hence, most of these materials are considered imperfect for application and often impair the quality of life. On the other hand, native tissues are living, multifunctional, and hierarchically ordered structures. "
Our comments:
That is a good acknowledgement of the situation with hierarchy of tissue morphologies.
In the p.6 one can read: "Over a hierarchical sequence, changes in the assembly and organization of mineralized collagen evolve to a more complicated arrangement of crystal platelets, plates, and lamellae....."
p.6-7: "At higher hierarchical assembly, the mineralized collagen fibrils in bones are almost always present as bundles or aligned arrays,.... '
p. 11: "There is definitely a need to further improve current technology in order to fabricate bone-resembling hierarchical organization over several length scales."
"The processing .....gap between the lower-level building units and the higher-order architecture could severely limit the practical application of these biomimetic materials...."
We can have this Summary:
1) The reveling great article by Liao et al., (2007) (Liao, S., Chan, C.K., and Ramakrishna, S., "Biomimetic Nanocomposites for Tissue Engineering," J. Bionanoscience, Vol. 1, No. 1, pp. 1-13(13), (2007)), openly speaks on the subject of hierarchy and scale dependency in tissue engineering, which is to some extend becomes more and more recognized. So far that is in the verbal, qualitative mode.
Even the close familiarity with many concepts and presentations in the biology media models, tissue modeling that will make a temptation to lay down a theoretical approach, models, which would correctly reflect the heterogeneity and polyscaling nature of biological subjects would bring in the status in the field that can be declared as a long shot unsatisfactory.
That is because of the scale description invalidity while with the homogeneous GO theorem the theory ground was developed.
Many issues even are not raised in the review -- no sense to fantasize about questions that belong to the beyond the horizon picture?
The main is - What is the connection between the exact interactive communications in properties (mechanical, chemical, biocompatible) for structures of composites at various scales?
2) It was of interest reading in this paper on the fact of acknowledgment of scale interaction and interdependency. Unfortunately, it is done as in most of similar acknowledgements in the way of verbal statements, hindering the means that without that kind of knowledge - researchers will not get closer to their aim as alchemists without the periodic table - they had no guidance to work with.
3) Also, what is the connection between the exact interactive communications in properties (mechanical, chemical, biocompatible) for structures of composites at various scales?
4) In Fig. 2 composites (p. 8), for example, the properties can be estimated, calculated with the high physical accuracy by HS methods.
5) The examples of media that depicted in Fig. 3 hierarchical
structure for scale composite properties, and what is more important -- its
design characteristics, those can only be mathematically correctly assessed
and modeled via application of the HSP-VAT methods, examples are in -
6) Reflecting to this paper's content -- and within our effort to advance the quantitative aspects of Biology and Medicine technologies, we would like to mention again that the only existing nowadays tools for understanding, modeling, simulation and design of hierarchical, heterogeneous structures and materials are grown within the HSP-VAT.
No other method exists, but the HSP-VAT, that has a more than 40 years of advancement from the commencement by first publication in 1967 and a reasonable modeling value results from 80s of the last century.
7) The most important answers we can get with the HSP-VAT hierarchical heterogeneous modeling and simulation:
Why nature does this or that for/with this biomaterial, tissue?
Why do the sizes of these pores or morphology of this scale medium has these characteristics?
What should be the properties of this or that constituent part, a phase in this material?
Can we improve or substitute the design and features of specific biomaterial?
How can we do better in the interphase between artificial and natural tissues?
What are the extracellular momentum and mass transport (calculated with a reasonable model, but not by balance equalities) ?
What are the bone tissue strength components? Not as of a homogeneous material which it is not.
What is the intracellular - extracellular exchange transport as the scaled phenomena modeled? Not on a verbal qualitative chemical language for separate molecules using the artificial molecular and atomic scales level with the graphical imaging over the membrane molecular filtration.
8) All these and other alike these questions can not be answered by experimental only work or by conventional one scale homogeneous physics modeling and simulation.
As authors mentioned in the paper:
"Understanding of such natural hierarchical nanofibril structures can lead to new design and fabrication concepts for use in tissue engineering. The ability to create hierarchical synthetic nanocomposites using self-assembly ........ methods creates the potential to engineer better tissue construct for repair and incorporation."
That will remain to be seen. Without the ability to characterize and model the hierarchical structure this is hardly possible to deliver, while patients won't buy the promises of good performance based on only experiments of short time scale or even going through the long time set up.
And the FDA as well.
9) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media in the sub-section -
as well as in -
Further down the road - we can find some of the studies by group of French-German workers publishing extensively, for example, starting with the paper by Joanny, J.F., Julicher. F., Kruse, K., and Prost, J., "Hydrodynamic theory for multi-component active polar gels," New Journal of Physics, Vol. 9, pp. 422-438,(2007), the many issues that are of interest as for the scaled and hierarchical description in biology.
From the Abstract:
"We develop a generic hydrodynamic theory of active fluids with several components. We take into account polar order and consider the case when one component is viscoelastic. Our theory is motivated by the cytoskeleton which is a network of elastic filaments that are coupled to active processes such as the action of motor proteins ..."
In p. 422+3=425 one can read: "In order to derive the constitutive equations, space is divided into volume elements" (emphasized by V.T.) "that are small compared to the length scales of the spatial structures under study. The central assumption is that each volume element is in a state of local thermodynamic equilibrium."
Our comments:
.....In homogeneous Thermodynamics, of course, the volumetric averaging traditionally exists, but it is wrongly used (because of the GO theorem) for heterogeneous subjects, media.
In the p. 422+3: "The energy of the full system is obtained by summing over the contributions of all volume elements. In the continuum limit this yields
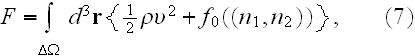
where

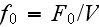 is the free energy density that only depends on the densities of the two
components."
is the free energy density that only depends on the densities of the two
components."
"
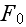 is the free energy of the system in the volume element
is the free energy of the system in the volume element

Our comments:
Here

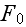 is the free energy of the system in the volume element
is the free energy of the system in the volume element

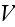 ,
while the volume
,
while the volume

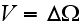 was not specified (just some volume, that's it), which is with a homogeneous
subject.
was not specified (just some volume, that's it), which is with a homogeneous
subject.
So, we don't know - How it is defined in reality, as we wrote in -
Also, how the bounding surfaces dividing the all components, if any of them?
As we see here -- in homogeneous thermodynamics also used the "continuum" limit, which for heterogeneous matter is often makes a wrong result (because of GO theorem used).
That equality (7) in heterogeneous media is of a different appearance.
p. 422+6: "Due to the polar nature of the cytoskeletal filaments, the system can be locally anisotropic. This introduces a hierarchy of order parameters, the most important ones are polar and nematic order.",
Our comments:
Better to say - "no comments." But the words were used "hierarchy of order parameters" - are from the one scale homogeneous statistical mechanics, where there is no real Hierarchy, and no real Averaging.
The words like "order parameter(s)," "polar" and "nematic order" have come from physics of the first half of XX century - to designate the things of not knowing the matter of a model - How to do modeling of complicated matter as composites, polymeric structures, where obvious not a homogeneous matter and at the same time the pretty unusual properties. The words "order parameter(s)" used by physicists caliber of Landau who himself created few equations in physics of different phenomena out of desperation for prescription of mathematics for them, governing equations. And he did not bother himself with the "invariantness" of these equations. Or any firm ground justification for deduction.
But now we know how we can do this. Through application of scaled approaches, strong enough mathematically.
p. 422+12: "Motivated by the description of the actin cytoskeleton, we have presented in this paper a hydrodynamic theory of three component active fluids, one of which is active and polar and represents the filamentous actin phase, while the other two represent monomeric actin and the cytosol (the solvent). Built on conservation laws and symmetry relations, the theory captures the essential features of the cytoskeleton and allows to address physical aspects of cytoskeletal dynamics. ",
Our comments:
These conservation laws have been invented and were written for a one-scale homogeneous matter, and are not applicable often for heterogeneous ones.
Summary:
1) All the content in the paper is explained in terms of homogeneous fluid media mixtures. That is the large monomeric units (particles) and cytoskeletal filaments network considered as "fluids". That move alone precludes the reasonable and realistic description.
2) Consider the scales for this medium's phases:
2.a) For filaments (actin of a cytoskeleton);
2.a.1) Microfilaments - approximately 6 - 8 nm diameter; actin monomer is 43 kDa of molecular mass; with the length of app. 0(10^2) nm;
2.a.2) Intermediate filaments (IFs) - app. 10 nm diameter, a length can be many 10^2 nm that is a real networks of IFs. Length of network branches could be (10^2 - 10^3 nm) - it is a real network. They are biochemically much more heterogeneous; have great tensile strength.
They are grouped into 6 classes of their proteins, masses of them (40-110) and up to 240 kDa.
2.a.3) Microtubules - external diameter are app. 25 nm; tubulin is a dimmer of 2 subunits of ~55 kDa.
2.b) Of monomer particles as - actin (56 kDa), G-actin units have 42 kDa, F-actin (filamentous) has 8 nm width and 16 [kDa/nm] mass molecular; tubulin - ~50 kDa molecular mass; alpha-actimin;
2.c) Cytosol's some molecular masses - in cytosol we have:
2.c.1) FABPs (fatty-acid-binding proteins); they contain as much as app. 5% of all cytosolic proteins;
2.c.2) Cholesterol is synthesized by enzymes in the cytosol and ER membrane -- so, the proteins used for this composition (synthesis);
2.c.3) Soluble lipid transfer proteins;
2.c.4) Hundreds of putative transport proteins;
2.c.5) Motor proteins;
2.c.6) Actin-binding proteins;
2.c.7) Enzymes macromolecules;
2.c.8) Myosin proteins as taken separately;
2.c.9) In cytosol is occurring the synthesis of proteins, fats, and initial steps in the release of energy from sugars.
In plant cells exists cyclosis -- the streaming inside of the cell, a circular flow of cytosol.
3) In pages (422-3 -- 422-6) is given the bulk schematic derivation of homogeneous mechanics (de Groot, Mazur, 1984) the two-component fluid model for monomeric "particles" (subunits) and a solvent fluid (cytosol).
4) In the further pages (422-6) -- (422-9) authors concluded development (again) of only homogeneous presentation of 3-"fluid" mixture following the steps described in [25] (de Groot, Mazur, 1984, Handbook on Homogeneous Thermodynamics).
5) What's wrong with such a development for the heterogeneous
media? The wrong issues are many; most have been concerned in our advanced
sections in the web -
And we talk about that below. Among main issues to discuss we would select the following.
6) Because the Biology Quantitative fields are following the other sciences in mathematical modeling with a lag of approximately 25 -- 30 years (may be more), that would be useful to reiterate here the 2 disadvantages that dumping the homogeneous Quantitative Biology in this area, because:
a) It is impossible to explain and analyze correctly the advanced experimental works.
b) It is impossible to use the such Homogeneous one scale Theoretical Biology to discover new effects, phenomena or design new method for biology applications.
7) Also, we need to recollect that the same or even more complicated homogeneous mixture constructions for a tissue engineering subfields filled out the medical literature in previous 2 decades. References are numerous. This approach by present authors is not the first of that kind in bio-medical sciences.
There are the homogeneous media approaches in biology based on the idealistic method that came from chemistry and named the 'theory" of mixtures. The biphasic, triphasic and so forth methods, all based on homogeneous thermodynamics assessment methods have been published for many years.
8) And what are the goods brought in by this homogeneous mixtures approach to bio-medical sciences throughout the last approximately 20 - 30 years? Nothing interesting, the funds have been spent for educational purposes primarily.
It must be stated that no serious results can be obtained with these simplification methodologies for polyphase by nature biomedia.
Conclusions:
1) While these qualitative homogeneous mixtures approach is a useful example, it is too far from the available today possibilities of quantitative biology, biological media and phenomena scale, hierarchical and heterogeneous description can have.
Some of them we have done in our biological studies, some are
open in one of the websites:
2) This is critically essential to say that all the like suggestions, approaches presented in papers published by biologists, theoretical biologists, (see multiple texts in references in pp. 4-2, 17) are actually very well-known theoretical constructions that have been used in Fluid Mechanics, Thermal Physics and Continuum Mechanics, Elasticity theory for at least 60 years.
Many of these constructions were published in those fields' literature sources for many times and for many years.
If this is a "discovery" of first principles for biologists ("theoretical biologists"), that is not the case for many, many other physical sciences. So, keep referencing, please.
3) Because all 3 types of elastic filaments in a cell serve the structural distinctive roles and have multiple recognizable and pretty different functions of a heterogeneous nature, it is imperative to consider them as the 3 types of separate particulate media, not fluids!
The cytosol itself is an aqueous mixture of multiple globular particles, proteins, enzymes, a part of light molecules and should be considered itself as a polyphase non - Newtonian medium.
We have developed some
fundamentals of Scaled Heterogeneous Polyphase Cytoskeleton's HSP-VAT theory
with some features in -
4) We are addressing these and close issues in our
sections on Cellular Biology Heterogeneous scaled media in
the sub-section -
as well as in -
***************************************************************************
Article by Günther, S. and Kruse, K., "Spontaneous Waves in Muscle Fibres, New Journal of Physics, Vol. 9, pp. 417- 430(417+13), (2007).
A hypothesis coming from the idea in the abstract:
"Mechanical oscillations are important for many cellular processes, e.g. the beating of cilia and flagella or the sensation of sound by hair cells. These dynamic states originate from spontaneous oscillations of molecular motors."
Here in this paper, we see also the Hydrodynamic model for a Visco-Elastic heterogeneous polyscale biomedium of muscle.
p. 419-3(417+2): "In general, the system is subdivided into volumes that are small compared to the large-scale structures of interest and that are, at the same time, large enough to allow for a thermodynamic (equilibrium) description."
p. 420 (417+3): "Under the assumption of local thermodynamic equilibrium, changes in the system's free energy can be expressed as
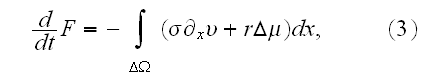
It can thus be written as a sum of products, where in each product, a
generalized flux is
multiplied with its conjugate generalized force......
...where the fluxes are taken to be the stress
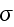 and the rate of
ATP-hydrolysis
and the rate of
ATP-hydrolysis
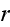 . The force conjugate to
. The force conjugate to
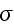 is the rate of
strain
is the rate of
strain
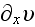 , the force conjugate to
, the force conjugate to
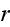 is the difference
is the difference
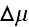 in chemical potentials of ATP and its hydrolysis products
ADP and
in chemical potentials of ATP and its hydrolysis products
ADP and
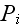 ,
,
 ."
."
Our comments:
This is the basic heaviest brick in the foundation of energy depiction as in the Homogeneous Thermodynamics.
The trick in this approach for description of the energy changing the form and undergoing transport via the space is that the numerous phenomena -- polyscaled by nature, could be in this way lumped altogether into the one or more terms with the very simple (and sometimes good for linear phenomena) procedures -- while the effect being declared with the some knowledge of its nature and then mathematically inserted in the form of some flux and its coefficient as in homogeneous hypothesis always did in thermodynamics of homogeneous matter.
Here the phenomena description for energy process is of the highest scale of generalization -- at the largest continuum level accepted in the model. Just from the beginning.
That means also that the all phenomena taken further in an explanation should be of the same scale as energy process stated.
Nevertheless, many observations that were put into the model further are of the much lower scale in their description, for example, motor proteins.
p. (417+5): "The motor filament as well as the polar filament are effective structures that result from averaging the parallel filaments in a sarcomere in the direction perpendicular to the sarcomere extension. The whole structure is immersed in a fluid of viscosity μ . "
Our comments:
Well, it is good that authors are recognizing the "averaging" necessity in this regard. Nevertheless, the averaging should be extended and provided out by mathematically correct procedures of HSP-VAT in two dimensions for the current problem.
p. (417+8): "Consider a chain of S half-sarcomeres, where the right end of a half-sarcomere is
simultaneously the left end of the subsequent element. "
Our comments:
Why to have only of a half-sarcomere chain? Completely wrong connections!
Summary:
1) In the paper by Günther and Kruse (2007) is given an attempt to describe mathematically clear the scaled phenomena in muscle fibers as via the homogeneous physics one-scale models for mass, momentum and energy of volumetric presentation of muscle fibers ensemble.
2) In page 417-4 (417+3) is given the balance equations of homogeneous medium based on assumption of local thermodynamics equilibrium (referring done to the book by de Groot, Mazur, 1984).
3) With no elasticity properties of the medium and governing equations due to this Upper scale description. Why is this with no elasticity -- because model conjectures the Hydrodynamic description of the processes? For the soft elastic medium -- the hydrodynamic model?
4) Synchronization of sarcomeres in muscle fibers are probably due to a collective effect of Bottom-Up local-non-local movements of adjacent protein molecules -- actin, myosin, together with the interconnecting titin macromolecules.
5) In ps. 417-6 (417+5) - 417-9 (417+8) is given the model of elasticity for half-sarcomeres (?) chain. Why the half of the structure element?
Because, apparently, authors can not do the averaging of the whole chain substructure to the continuum mechanics effect?
For example, authors wrote : "In the following, we will use a mean-field approximation, which consists of assuming that all motors in the half-sarcomere have the same spring extension,... " ?
6) The elasticity of muscle fiber as given in eq-ns (9) --(11) (p. 417-7 (417+6)) is obviously heuristic by nature, because the scaled local-non-local phenomena is lumped together by just mechanistic conjectures.
To move to the upward to the continuum mechanics muscle fiber model authors got to the stage of artificial reasoning in pages 417-10 - 417-11.
7) To have an ability to talk about and get some continuum mechanics conceptual analysis authors invented the "continuum limit" algorithm in pages 417-10 - 417-11, purely frivolous in nature.
They referring to their own definitions of volumes and sub-volumes?
"In general, the system is subdivided into volumes that are small compared to the large-scale structures of interest and that are, at the same time, large enough to allow for a thermodynamic (equilibrium) description."
That volumetric exercise is not a volumetric heterogeneous averaging, as one might imagine.
No, this is the homogeneous medium averaging used in the thermodynamics of a one scale.
Conclusions:
1) In conclusion we might emphasize the note that this kind of scaled biological subject -- the extremely complex multiphase, multiscale mechanics of muscle fibers can not be submitted to and treated as the one scale homogeneous physics and mathematics field, if the aim is a serious scrutiny. With the consecutive modeling by means of conventional one-scale hydrodynamics mathematical models.!?
O.K., everyone can do whatever the professional experience advises him to do, but still exist the natural features and reasons for that or this approach, to make the object under consideration either closer to original or just bent into the sought form.
This is an example of -- How not to do such a theory and modeling for polyphase polyscale matter.
2) These kinds of hierarchical
phenomena in muscles we had subjected to scaled analysis and treatment in
1993-94, and it can be seen in -
There have been following years of research over this subject of muscle tissue modeling and simulation.
3) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media in the sub-section -
as well as in -
********************************************************************
The theoretical construction by Doubrovinski, K. and Kruse, K., " Cytoskeletal waves in the absence of molecular motors," Europhysics Letters, Vol. 83, pp. 18003-p1- 18003-p6, (2008); is about modeling of the really polyphase matter of the cytoskeleton.
From the Abstract:
"Waves are a ubiquitous phenomenon in the cytoskeleton of cells crawling or spreading on a substrate. In theoretical analysis, cytoskeletal waves have been attributed to the action of molecular motors that actively cross-link cytoskeletal filaments..."
"we find traveling waves even in the absence of molecular motors. In a confined domain the system can organize into a pair of counter-rotating spirals that emit planar waves." ??
In p. 18003-p2 one can read: "In the present work, we explore a possible mechanism for the generation of actin waves in the presence of Hem-1. In contrast to previous theoretical investigations of active filament systems, we neglect the effects of molecular motors. Specifically, using periodic boundary conditions, we find planar waves and moving spots."
Our comments:
It is hard to believe - that in the absence of motors, still vibrations occurred?
Still, the source of motion could be in numerous source terms in homogeneous governing equations (1) -- (5)?
In p. 18003-p2 one can read: "The distribution of
actin filaments is given by the density

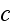 of filament centers, which depends on the position
of filament centers, which depends on the position

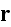 ,
on the orientation
,
on the orientation

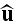 ,
where \
,
where \

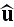 \
\

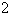 = 1, and on the filament length
= 1, and on the filament length

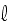 as well as on the time
as well as on the time

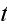 .
.
The dynamic equation for

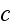 reads [16] (this is authors own publication in Phys. Rev. Lett. (2007))
reads [16] (this is authors own publication in Phys. Rev. Lett. (2007))
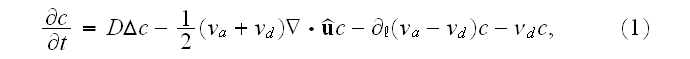
where

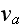 is the polymerization velocity at the plus-end,
is the polymerization velocity at the plus-end,

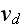 the depolymerization velocity at the minus-end,
the depolymerization velocity at the minus-end,

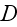 an effective diffusion constant that accounts for fluctuations
in the system, and
an effective diffusion constant that accounts for fluctuations
in the system, and

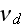 the filament detachment rate."
the filament detachment rate."
Our comments:
Here we see a number of adjusting parameters accepted in the midst of 20th century just to describe the problem with the language at that time available and being in possession of physicists.
Among those artificial parameters (described with the help of semantic definitions) as, for example:
1.1) First of all, if one uses the Homogeneous equation for the Upper scale physical presentation as in (1) then this equation is invalid by deduction. For its development was used the homogeneous GO theorem and this is invalid mathematical procedure for a heterogeneous medium.
1.2) Then, all the set of variables and parameters -

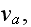

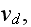

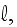

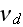 and
and

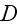 are
non-specific coefficients, that is - these are the adjusting parameters for
the one scale homogeneous model. The last one nobody knows how to determine -
the diffusion rate for the density of filaments centers? What is it?
are
non-specific coefficients, that is - these are the adjusting parameters for
the one scale homogeneous model. The last one nobody knows how to determine -
the diffusion rate for the density of filaments centers? What is it?
Further in p. 18003-p2:
"We do not consider
rotational diffusion, which is negligible if the
filament concentration is large enough. The nucleation of new filaments is
accounted for by the boundary condition at

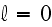 .
.
We assume that the density of nuclei is fixed
by the amount of nucleators and write

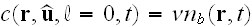 ,
where
,
where

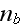 is the density of nucleating proteins bound to the membrane. That is, only
nucleators bound to the membrane are active. The parameter
is the density of nucleating proteins bound to the membrane. That is, only
nucleators bound to the membrane are active. The parameter

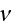 is a constant.
is a constant.
The densities

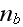 and
and

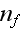 of proteins nucleating new
filaments (Hem-1) bound and not bound to the membrane,
respectively, evolve according to the equations
of proteins nucleating new
filaments (Hem-1) bound and not bound to the membrane,
respectively, evolve according to the equations
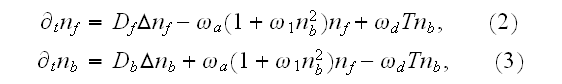
Here,

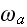 and
and

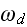 ,
respectively, denote the rates of attachment to and detachment from the
membrane. The term
,
respectively, denote the rates of attachment to and detachment from the
membrane. The term

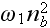 accounts for cooperativity (it is in the paper, may be -
cooperation?) during binding of nucleators to the membrane. As we will show
below, this term is the lowest-order term that is able to
generate an instability
of the homogenous isotropic state. The parameters
accounts for cooperativity (it is in the paper, may be -
cooperation?) during binding of nucleators to the membrane. As we will show
below, this term is the lowest-order term that is able to
generate an instability
of the homogenous isotropic state. The parameters

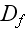 and
and

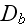 are again effective diffusion constants that account for fluctuations in the
system.
are again effective diffusion constants that account for fluctuations in the
system.
Finally,

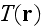 denotes the amount of actin filaments overlapping with a point
denotes the amount of actin filaments overlapping with a point

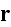 in space:
in space:
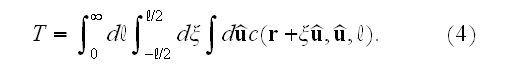
This completes the specification of the dynamic equations.
In order to analyze eqs. (1)--(4) we introduce a
hierarchy of order parameters and coarse
grain [16]."

Our comments:
We've already spoke on the "order parameter" words
used mostly authors as a magic words for explanation what authors don't
know themselves - if L.Landau did not?
In these (2)-(4) equations there is the same homogeneous
medium modeling mode for obviously heterogeneous phenomena.
1) Regarding the homogeneous governing equations for heterogeneous polyphase media - then, it is wrong by deduction as we told above in the text.
2) Here again, all the set of variables and parameters -

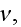

 and
and

 are
verbally denoted non-specific coefficients along with
are
verbally denoted non-specific coefficients along with

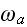 and
and

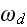 ,
,

 and
and

these are the adjusting parameters for the one scale scaleless homogeneous model.
The coarse graining gave authors the following governing equations for "averaged" over the 3D infinite domains (Cartesian space) functions (moments)
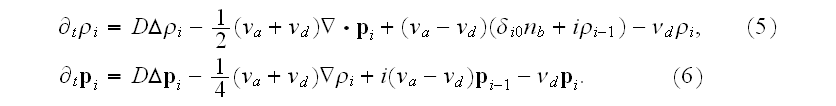
The same remarks should be applied to these "quasi-averaged" equations as we noted above.
Plus - All these additional interchange terms in (5),(6) and additional force fields added in p. 18003-p4 are somehow incorrect representations of additional interscale and interphase terms that present in the Upper scale HSP-VAT governing equations for filaments and cytoplasm (media) heterogeneous momentum and elasticity in a cell.
In p. 18003-p4 one can read:
"As,
eventually, we will coarse grain the fields, we evaluate the force on a
filament by calculating the derivative of

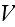 at the filament center
at the filament center

 .
The force field resulting
.
The force field resulting
from the potential at a point

 is thus given by
is thus given by

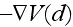 ,
where
,
where

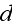 is given by
is given by

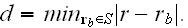 From
this force field, we obtain additional terms on the
right-hand sides of the coarse-grained dynamic equations (5) and (6), that
read
From
this force field, we obtain additional terms on the
right-hand sides of the coarse-grained dynamic equations (5) and (6), that
read

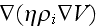 and
and

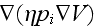 ,
respectively. Here,
,
respectively. Here,

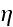 is the mobility of the filaments, which we assume to be independent of the
filament length. "
is the mobility of the filaments, which we assume to be independent of the
filament length. "
Our comments:
Well, the artificial statements given with the artificial number of parameters and coefficients:
Also, in the figs. 3 and 4 shown the Heterogeneous fields given in a confined domain with the periodic boundary conditions!
As it is shown in the HSP-VAT the periodic Homogeneous boundary conditions are unnatural and incorrect boundary conditions for the scaled problems -- When we use to solve the problem on the Lower scale and seeking the generalizations and effective parameters, characteristics, and simply the description of fields on the Upper physical scale phenomena ascribed to the same or better quality of detail, and features taken into account.
Summary:
1) According to the known up to nowadays features - the process of creation, work - functioning of a single actin filament, depolymerization of filaments, as well as the collective cooperative effects (actions) by array of filaments and filament network - all those are looking as the 3-scale physics for description and modeling:
1.1) the amount of monomers and other proteins are bathed by the aqueous polyphase liquid - cytoplasm to start the modeling with;
1.2) the work of polymerization-depolymerization and filamentous and molecular motors momentum (if only taken) transport in the cytoplasm - are the second scale processes with the specific scaled description and modeling;
1.3) the scale of filament network and the elastic- viscoelastic behavior of that network inside of the cell is the 3-rd scale challenge which biology faces for many decades.
2) Well, according to this 3-scale phenomena schematic (scheme), the homogeneous one-scale dynamic equation (1) in p. 18003-p2 along with the equations for proteins nucleation (2), (3) are hardly to be considered as a closely relevant (rather incorrect) as the scaled phenomena expressions.
3) The p. 18003-p3 construction of order parameters and coarse grain procedures is unnecessary step for the generalization and studying the proposed polyscale process scheme.
That was done as the frame tools used in the homogeneous 60-50 year-old One-scale One-phase mechanics. Which is being well greated in many orthodox journals.
4) Fortunately, today the more realistic polyscale polyphase physics and modeling tools exist (HSP-VAT) for scaled description of the cell mechanics.
Conclusions:
1) This is not a correct model and physics for this part of the scaled cytoskeleton mechanics in the cell.
2) There should be developed the really scaled mathematical and physical models for this collective polyscale mechanism of locomotion (migration) of the cell and within the cell.
This should be done immediately, as long as incorrect obsolete physics schematics of old homogeneous constructions started on to appear since the beginning of this century.
3) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media in the sub-section -
as well as in -
******************************************************************
Here is one of the US theorists with the multiple involvements into the biology modeling - Prof. Newman, T. J., "Modeling Multicellular Systems Using Subcellular Elements," Mathematical Biosciences and Engineering, Vol. 2, No. 3, pp. 611-622, (2005).
From the Abstract:
"We introduce a model for describing the dynamics of large numbers of interacting cells. The fundamental dynamical variables in the model are subcellular elements, which interact with each other through phenomenological intra- and intercellular potentials. Advantages of the model include i) adaptive cell-shape dynamics, ii) flexible accommodation of additional intracellular biology, and iii) the absence of an underlying grid.
We present here a detailed description of the model, and use successive mean-field approximations to connect it to more coarse-grained approaches, such as discrete cell-based algorithms and coupled partial differential equations. We also discuss efficient algorithms for encoding the model, and give an example of a simulation of an epithelial sheet. Given the biological flexibility of the model, we propose that it can be used effectively for modeling a range of multicellular processes, such as tumor dynamics and embryogenesis."
Our comments: Oh, no-no, not for those situations. It is too far.
In p. 612 we can read:
"In this paper we introduce a framework for modeling multicellular systems which is designed to allow simulation of large numbers of cells in three dimensions, but which also allows for adaptive cell-shape dynamics and the accommodation of successive degrees of intracellular biology. This framework uses subcellular elements" (defined below) as the fundamental dynamical variables, along with overdamped Langevin dynamics [19, 27] for temporal development of the system."
In paper in p. 613 we can read: "For simplicity,
consider a system with a constant number

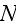 of cells in three spatial dimensions, with each cell being composed of
of cells in three spatial dimensions, with each cell being composed of

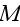 elements. We label an
elements. We label an
individual cell by

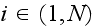 and an element in cell
and an element in cell

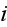 by
by

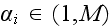 .
For ease of discussion we assume that chemical signaling is absent from the
system, so that cells respond purely to local biomechanical interactions."
.
For ease of discussion we assume that chemical signaling is absent from the
system, so that cells respond purely to local biomechanical interactions."

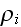 average density field
average density field

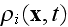 is the average density of cell elements in a cell;
is the average density of cell elements in a cell;
Our comments:
So, this is the many-body approach with the point objects which, even when at the scale of many orders of magnitude, are less then the current objects (as usual, by the way) still have the volumetric physical properties.
A great attention should be paid to these words of initial
statement basic definitions - that means, author just substituted by a graph
(diagram construction), by a classical Theoretical Dynamics Mechanics scheme - a
set of

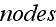

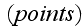 and
the connecting them edges (bonds) with their properties. Finite mathematics,
descrete mathematics schematics for the Continuum mechanics subject.
and
the connecting them edges (bonds) with their properties. Finite mathematics,
descrete mathematics schematics for the Continuum mechanics subject.
This XVIIIth century approach was not good for the physics of XXth century, not saying of XXIst one .
And all that Statistical Mechanics constructions done for the Continuum mechanics described objects - which is much more accurate and exact in the depiction of phenomena.
Further in p. 613 we can read: "In this case, the position
vector of element

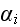 is taken to change in time according to three processes:
is taken to change in time according to three processes:
(i) a weak stochastic component, which mimics the underlying fluctuations in the dynamics of the cellular cytoskeleton;
(ii) an elastic response to intracellular biomechanical forces; and
(iii) an elastic response to intercellular biomechanical forces. We assume
further that the elements' motion is over-damped, so
that inertial effects can be ignored. The equation of
motion for the position vector of element

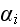 takes the form:
takes the form:
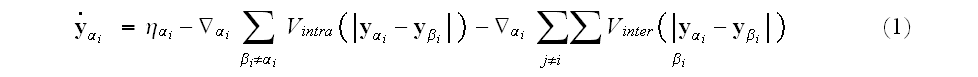
On the right-hand side, the noise term

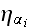 is a Gaussian-distributed random variate with zero mean and correlator
is a Gaussian-distributed random variate with zero mean and correlator
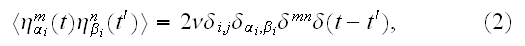
where

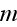 and
and

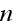 are vector component labels in the three-dimensional space. The second and
third terms on the right-hand side of equation (1) represent, respectively,
are vector component labels in the three-dimensional space. The second and
third terms on the right-hand side of equation (1) represent, respectively,
intra- and intercellular interactions between the elements.
These interactions are completely characterized by the
phenomenological potentials

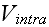 and
and

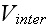 .
At this level of description, all relevant biological detail must be
encoded into these two potentials. The elemental
composition of cells, along with the inter-elemental potentials, are shown
schematically in Figure 1."
.
At this level of description, all relevant biological detail must be
encoded into these two potentials. The elemental
composition of cells, along with the inter-elemental potentials, are shown
schematically in Figure 1."
" We have assumed that "two-body" potentials are sufficient to describe the dynamics. " "
"For given biological applications of this modeling framework, one must intuit
(or, better, derive) reasonable forms for

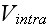 and
and

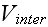 .
For illustrative purposes,.."
.
For illustrative purposes,.."
In p. 614 in continuation we can read: " consider a population of cells which are weakly adhesive to one another. Subcellular elements both within and between cells will be mutually repulsive if their separation is below the equilibrium size of an element. (V.T. - Oh, no-no, this is all about the particle physics, not of biology's cells).
For separations larger than this size, the elements will be mutually attractive, but with the strength of attraction falling off rapidly with separation. These properties can, for example, be conveniently encoded via a generalized form of the Morse potential, (V.T. - and parameters in the Morse potential energy function are the adjusting variables, especially in the Top-Down sequence) which is commonly used in physics and chemistry to model inter-molecular interactions [24]. The (generalized) Morse potential has the explicit form
([24] L. I. Schiff, Quantum mechanics, 3rd ed., McGraw-Hill, Singapore, 1968)
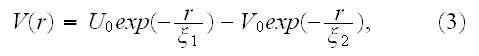
and is illustrated in Figure 2. It is straightforward
to evaluate the position
and depth of the attractive potential minimum
in terms of the four parameters
(
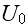 ;
;

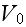 ;
;

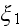 ;
;

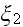 ).
).
In a simple application of the element model, one can use Morse potentials for
both

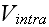 and
and

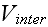 ,
with parameters chosen to ensure that the former has stronger inter-elemental
adhesion than the latter. This condition is necessary, in this simplest
version of the model, to maintain the mechanical integrity of the cells."
,
with parameters chosen to ensure that the former has stronger inter-elemental
adhesion than the latter. This condition is necessary, in this simplest
version of the model, to maintain the mechanical integrity of the cells."
Our comments:
1) These tools of "statistical mechanics, many-body physics" - they don't work well for many-body field and for particle physics as a whole, and they are obsolete and in part are incorrect because of the fundamental assumptions put in derivation of the governing equations (using definitions of point-like particles, homogeneous GO theorem, and incorrect averaging procedures - coarse graining).
Over again - mostly because of the two reasons (there are others), but the very mortal mathematically (and physically, as pointed out mostly grounded by R.Santilli)- they represent the objects as the point-like phenomena which they are not, and they represent in deductions every aspect as of the use of the Homogeneous GO theorem for the definitely Heterogeneous fields and objects of interest.
Also, they represent the fields of interest - particles as if they would be hanging out in a vacuum. Remember, the vacuum is the very subject where the many particle physics phenomena occur. "Active" vacuum now is known as the pretty rich medium in action, the active force field of interaction. All that is lost in old Statistical Mechanics.
2) All the fields and forces in this study are artificial; all of them appeared as a result of imaginary interactions without a field of interaction.
3) What is the intracellular interaction potential

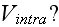 Morse potential? What is this? And what are its parameters? Just
numbers.
Morse potential? What is this? And what are its parameters? Just
numbers.
Is it electrical potential ? Nope.
What a potential we can have, if the model (phases, media, more strictly) performs interacting via known fields (physical) and this is essential?
What is the extracellular interaction potential

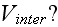
What are their connections to the continuum fields of extracellular space or other cells environment?
4) What is the field of noise

 (a Gaussian distribution field)? Exactly, what is it?
(a Gaussian distribution field)? Exactly, what is it?
Meanwhile, in the HSP-VAT this kind of effect has the precise calculable nature.
5) What determines the concentration field ?
All these and myriad of other questions have only perhaps adjustable connections to the fields ascribing the biophysical behavior of cell and tissue.
In p. 615 we can read: "In the first
of these coarse-graining steps, we replace the element model by a subcellular
density model, in which the discrete elements within a given cell

 are
replaced by a smooth average density field
are
replaced by a smooth average density field

 .
We stress that a separate
density field exists for each cell in the system, and that these density
fields are
strongly correlated to one another. To proceed, we first recast the
subcellular
element model in terms of the probability distribution of individual elements.
We define the probability distribution of element
.
We stress that a separate
density field exists for each cell in the system, and that these density
fields are
strongly correlated to one another. To proceed, we first recast the
subcellular
element model in terms of the probability distribution of individual elements.
We define the probability distribution of element

 by
by

 ,
where
,
where
the angled brackets denote an average over the noise

 .
Starting from equations
.
Starting from equations
(1) and (2) we use standard methods [19, 27] to derive an equation of motion for..."
Our comments:
Well, and all this old fairy-tale instead of just setting up the Lower scale continuum model for a cell - which is still the continuum media many scales down the sequence until we get to the atomic scale. And that the atomic scale promises to let us liberation from the shackles of conventional MD while scaling down properly.
In p. 616 we can read: "

 ,
which takes the form
,
which takes the form
where

 is the "two-element" distribution function. The equation of motion for
is the "two-element" distribution function. The equation of motion for
this two-element distribution will involve the three-element distribution, and so on.
The simplest truncation scheme to break the hierarchy of equations is the
mean-field approximation (MFA), in which the statistical correlations between
elements are discarded. Within this MFA we have

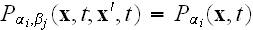

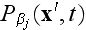 .
.
We now define the subcellular density of cell

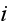 via
via

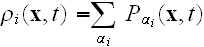 .
.
Summing over

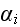 in equation (4), and imposing the MFA, we find a closed equation for this
subcellular density function, which takes the form of an advection-diffusion
equation:
in equation (4), and imposing the MFA, we find a closed equation for this
subcellular density function, which takes the form of an advection-diffusion
equation:
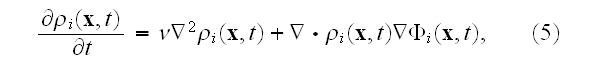
where the velocity potential experienced by the density field of cell

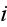 is given by
is given by
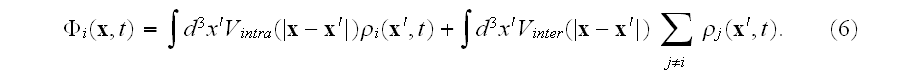
The MFA used to derive this density equation will typically be good when the number of elements used to define the cell is very large.
The density representation may well be interesting to explore from an
analytical standpoint; however, it is probably not so useful for numerical implementation. For simulation of

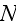 cells, one must simultaneously integrate
cells, one must simultaneously integrate

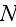 coupled partial differential equations on a fine three-dimensional grid. As we
shall see in the next section, the underlying element model, expressed in
equation (1), can be very efficiently encoded for simulation with no need of
an underlying grid."
coupled partial differential equations on a fine three-dimensional grid. As we
shall see in the next section, the underlying element model, expressed in
equation (1), can be very efficiently encoded for simulation with no need of
an underlying grid."
Here

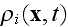 is the average density of cell elements in a cell
is the average density of cell elements in a cell

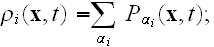

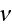 is the parameter seen in eq. (2);
and
is the parameter seen in eq. (2);
and

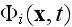 is
the velocity potential in a whole problem's domain, or simply the 3D space as
long as the spatial integrals used in deduction are undetermined with regard
of this??
is
the velocity potential in a whole problem's domain, or simply the 3D space as
long as the spatial integrals used in deduction are undetermined with regard
of this??
Our comments:
Given below after 617-618 pages equations.
In pp. 617-618 we can read about the further and final deductions: "We can use the density equation (5) to coarse-grain to another scale - where now only gross properties (which we refer to loosely as "moments") of the subcellular density field are used to characterize the cell. This coarse-graining step is analogous to a multipole expansion in electromagnetism.
(No - no, that is not as such, no. See our "Electrodynamics" section.)
.......
As shown in that work, a further MFA applied to equation (9) leads to a closed
equation for the density of cells, which is defined as
We omit the details here and simply give the final result:
where the coarse-grained velocity potential

 for the cell density has the form
for the cell density has the form
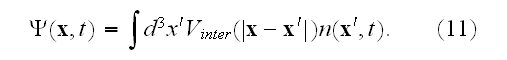
A rigorous derivation of this last step has been given by Stevens in the context of chemotaxis [25], and uses the limit of infinite cell number, with an appropriately scaled chemotactic coupling.
Finally, after three levels of coarse-graining, we have arrived at a partial differential equation for the cell density, as given in equations (10) and (11).
As mentioned in the introduction, this level of description has been widely used to describe the large-scale dynamics of cell populations. However, as should be clear from this analysis, a great deal of statistical information and smaller-scale biomechanics must be discarded at this scale."
Here

 is the global density of cells
is the global density of cells
 and
and

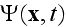 is the coarse-grained velocity potential (11).
is the coarse-grained velocity potential (11).
Our comments:
These equations (5) - (11) especially (5),(10) are of pure speculative nature based on the procedures developed in many-body and statistical mechanics for the point-like indistinguishable particles arrays!
And by using the invalid for heterogeneous media truncations rules for the Mean-Field Approximation (MFA) governing equations.
We can not get equations (5),(10) with the heterogeneous GO which are the WSAM theorems application, period.
What determines the "concentration fields in (5),(10) ? The GO theorem application.
Well, but the GO theorem can not be used for a particulate medium Upper scale (averaging), or coarse graining as it it used in statistical mechanics. What to do in this problem?
All those adjustable functions as

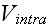 ,
,

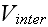 ,
noise term
,
noise term

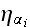 ,
and their numerous parameters are just pure speculative
adjusting functions and constants, baring nothing or very little of the real
physics related to the collective interactions of fields, phases, biochemical
characteristics of a cell, extracellular environment, etc.
,
and their numerous parameters are just pure speculative
adjusting functions and constants, baring nothing or very little of the real
physics related to the collective interactions of fields, phases, biochemical
characteristics of a cell, extracellular environment, etc.
Also, these final like equations for the global density of
cells

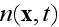 bare
nothing useful for the problem stated!
bare
nothing useful for the problem stated!
Because, we at any moment know that this number of cells exists and they are within the assigned medium, that's it. Regarding their redistribution, that has no sense to consider seriously because the great number of adjusting parameters can force cells move in any direction even might with the speed of light?
The motilities and shapes of cells have nothing to do with the pure mathematical speculations for the point representations of them, if those are only applied for model deduction, period.
Concluding remarks for this paper:
1) This paper is misleading the workers in the field of theoretical biology, for biologist who are not theoreticians it gives wrong knowledge, while regarding students these constructions from particle physics is screwing their education due to misrepresentation of the subject matter.
The poor understanding and the old fashioned traditional approaches that people, mostly physicists, apply to concepts and model development for biological subjects is not surprising me, rather depressing.
I got familiar with the similar vision by physicists and mechanical, electrical engineers that started working for nanotechs, and biotechs during the last like 8-10 years.
People, never thought of scaling or averaging issues, suddenly started responding to the challenge with the same 50-60-year-old tools, as used for statistical physics and particle physics in the first half of XX century. Where particles are thought as of objects with the point-like features?!
I am sure most of physicists who do "statistical mechanics (SM) for biology work" are familiar with these discussions on the validity of point particles - no volume, no features apart of those we would like to assign to.
Unfortunately, workers-physicists prefer to work with biological matters - those are polyscaled, in the same way as particle physicists pretend to work with volumeless particles.
Meanwhile, considering that the biological objects are the point-like items is the idealization used in physics in the middle and beginning of the XXth century, when they did not have vision and mathematics for the scale dependent problems.
That construction of order parameters and coarse grain procedures are simplifying (not simplistic) tools those were designed out of desperation in the middle XX century and designed for well adjusting to the some averaged experimental results.
Physicists in biology might know that the multibody problems are the Two Scale problems, as such by nature of statement. The point is that researchers are looking for some "bulk" averaged characteristics and fields -- and those are from the Upper scale. Nevertheless, it is really treated in multibody field as for the scale singular, because all the parameters and characteristics are adjusting as set-up by the nature of their definitions and determinations.
Being within the concept of the one scale for the entire scaled problem is not helpful to solve the multibody task, even the understanding and correct statement is impossible. We would be in the same situation as it was for centuries, when multibody problems were considered unsolvable.
Also, the most known techniques in traditional SM many-body
problem are approximate by nature, while the university communities are not
ready to accept this stature, see in our -
and in any other subsections in this website.
When I was doing the scaled and hierarchical studies at the University of California Los Angeles, I was told that the mathematical section, research body at that university was quite busy doing the multiphase (Homogeneous anyway) statements math. Where are those studies now and who knows what they've done after many-many years that passed at that research?
And at the same time the governments of many countries continue to fund many universities, institutions in hope that the needed science pertained to the rush with the mathematics and physics regarding the nanotech and biotech trend concerning the "multiscaling" would be overcome.
2) Meanwhile, using the consequences of Heterogeneous
Gauss-Ostrogradsky theorems (WSAM theorems), not a homogeneous GO of the XIXth century,
every science, where the tools of polyscale physics and mathematics of HSP-VAT
were applied, was having advances throughout the last 20-25 years to the new
level of stature. Even some textbooks problems had been solved as they should
be for the scaled problems in physics, for the first time and exactly, for
example in -
and others in this website communicating directly with issues raised in:
While these results have not been obtained with any fashion of multibody (many-body, as traditional reading spells) procedures, or any other "multiscale-like" mathematical theory or model that are even stated incorrectly.
In one of our simulation studies with the point-like objects transport in heterogeneous environment it was interesting to admit the evident discrepancies with the conventionally stated transport solutions (and that is using some of the traditional techniques as the Monte-Carlo one) -
3) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media and in the sub-section -
as well as in -
*********************************************************************
Not in for the first time, but unfortunately not for admitting some useful input, still we need to mention here again the publications by A.Bejan in a content related to scaled, hierarchical description claim specifically for biological sciences.
We have had the lengthy analysis on that in few places of this website, and what is more related to biology (the paper by -
Dai, W., Bejan, A., Tang, X., Zhang, L., and Nassar, R., "Optimal temperature distribution in a three dimensional triple-layered skin structure with embedded vasculature," J. Appl. Phys., Vol. 99, pp. 104702-1- 104702-9, (2006)); that piece was posted at -
In the text shown that there was no scaled description and proper modeling, but the verbal speculation on the subject.
Practically in all studies published in the fields of microbiology, cellular biology, structural biology, systems biology the subject matters are taken as of the "anthropogenic" point of view - what is available and seems important to us should be taken for the persuasion on our goals and results.
Here we talk about the perception of sizes in cellular biology that all "need" to be bent to our understanding of size in physics as of from our world which we can touch, assess, make an opinion about, etc.
And all that can be, OF COURSE, of the one scale perception - after all, we all have only Cartesian 3D world with the one scale measure - the meter! One ruler for all - just some factor to take.
This perception drives everything right now in structural biology. Any tool uses the one scale physics, and even when people spell out the words on the "multiscaling" as, for example, in Biophysical Journal, it's just the verbal description of different scales physics phenomena.
Without Scaleportation - because what is used in studies for connection of each scale models and their results is the parameterization "based on properties from the higher-resolution models," and from some experiments, which is the adjusting or "coupling" of neighboring scales modeling effort. But not a Scaleportation -
That is the lack of understanding and the segmentation in science probably are the reasons for the "coupling" mode scale modeling happening.
Also important is the stance on - What kind of scales is usually spoken about, is worked with, and probably understood to some degree in biology, especially in structural biology?
Exclusively, or almost exclusively it is down to the atoms? And we are not talking about subatomic scales principles physical instruments based on.
Why is that, if an ocean of subatomic scales particle physics, nuclear physics phenomena are relevant to the biology effects?
Subtle effects as biologists say? Is that the boundary of workers knowledge base, or what?
In some fields of study the Bottom-Up sequence of scales is so unusual that it is named as an "Inverse" method or Modeling? Which is strange.
We would talk on that in some sub-sections of this website.
From this kind of standing, as usual, we consider few researches in the cellular biology multiscale area.
The first we would look at is the recent findings on macromolecular assemblies topic published in "Nature":
Alber, F., Dokudovskaya, S., Veenhoff, L.M., Zang, W., Kipper, J., Devos, D., Suprapto, A., Karni-Schmidt, O., Williams, R., Chait, B.T., Rout, M.P., and Sali, A., " Determining the Architectures of Macromolecular Assemblies," Nature, Vol. 450, 29 Nov., pp. 683 - 694, (2007).
We had analyzed the work and collected a number of issues to discuss (and with workers of the study. Nonetheless, they hided from the open discussion - we send them an email suggesting to answer, or to make rebuttal to a few questions) regarding their work polyscale mathematical understanding and modeling performance. Later on, we'll put some of these issues to this open forum. That was in ~2009.
Right now, we say some words at the beginning on the conduct regarding the scaled presentation of this problem by authors themselves.
One can read in p. 683 : "A mechanistic understanding of the cell requires the structural characterization of the thousands of its constituent biological assemblies^1. So far, conventional approaches have provided a valuable but limited window into the structures of these assemblies.
For example, X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy can resolve the atomic details of individual proteins and small complexes, whereas electron microscopy produces morphological maps but can lack the ability to identify and detail specific components in the map of the whole assembly. As a result, we do not yet have atomic-resolution structures, or even low-resolution representations, for the vast majority of complexes in the cell."
In this the very resourceful study workers biologists actually tried to explore the venue with Conventional One-scale Homogeneous Physics to provide the fake Scaled (!) presentation and study of ensemble of cell's Nuclear Pore Complex, where nonetheless are given figures with imitation of the Heterogeneous bio-tissues.
Down the text one might spot in p. 685 the key "Figure 2: Structural representation of the NPC. a, Hierarchical representation of the NPC that facilitates the expression of the experimental data in terms of spatial restraints. Formally, we define the whole NPC assembly A as a set of symmetry units U of two different types with eight instances each, referred to as half-spokes....."
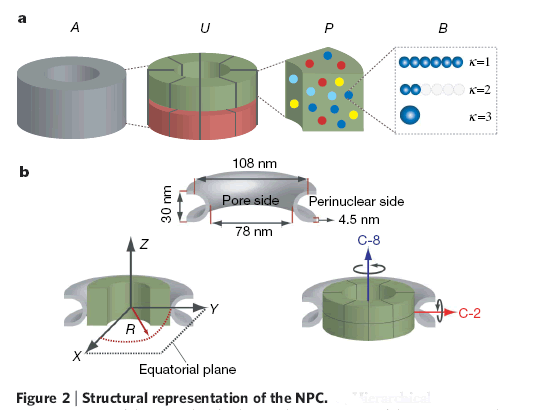
The real Hierarchical structure of the cell's Nuclear Pore Complex (NPC) - consisting of four (4) scale morphologies with different structural and physical functions. Nonetheless, the great mortal error is depicted on the third scale P with the Figure (P) for 3D structure of molecules - they are still drawn as in the Homogeneous block with molecules. And besides - the three other scale selected Volumes for analysis are also the Heterogeneous Polyphase Volumes with their scale biophysical special features. Workers just don't know how to make a figure and treatment - research of Polyphase volumes here in openly biophysical study - still in usual pictures in medicinal literature doctors know how to draw the piece of Polyphase tissue. So far described in a pure biological semantical language. Meanwhile, in HSB Each scale has components of physical description and mathematical language and models. These models are not and would not being available to biological communities - unless they handle somehow HSB education and tools.
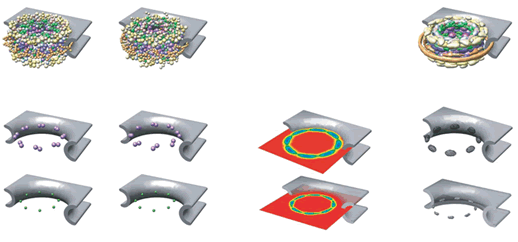

Our comments:
The text statements and the Figures in the paper tell us about the pure need for scaled representation and solution in terms of hierarchy of the structure and the function of the NPC. Nevertheless, in the study there is no really hierarchical model building -- presented a morphological construction of the NPC. That is a desirable, but the "fake" hierarchy Top-Down. While authors can not present and do the Bottom-Up sequence - that is the primary goal to understand the FUNCTION of NPC.
Our Summary:
1) We would like to praise workers of this gigantic job done for the determination of the morphology of specific protein complex in a cell.
At the same time, our goal is to discuss the methods used for this (and any other) Polyscale Heterogeneous (PHt) microbiology, structural biology, cellular biology, and other definitely PHt biology field studies.
2) The problem here, the main issue of this analysis is about the scaled description of the evidently scaled collective interaction of many hundred of proteins.
Roughly talking we have, we can take for simplicity the three different scales participating differently in the Nuclear Pore Complex (NPC) function:
a) the scale of a separate molecule (as amino group, for example) in a macromolecule, protein, or in a solvent, or in a soft tissue as the NPC is, or etc. - ~0.2 [nmSc], (Scale spatial);
b) the scale of a single protein - (1-5) [nmSc]; which is not walking alone, but imbedded into a polyphase solvent, or docked to other protein(s), or is the part of an assembly;
c) and the scale of constitutive protein complexes - ~(10 - 50) [nmSc]; in the known and much studied nuclear pore complex assembly NPC, of 456 proteins is only known.
3) In no way we would like to diminish the result, the great result in the paper. We have to set up a tone to discuss the features, the insufficiencies that surely preclude the future research over this and other assemblies of macromolecules, proteins, etc.
The problem is with the function of the macromolecular assembly.
The discussed result is actually the establishing bounds for measurements, the analysis of experimentations, but not the explanation of morphology, of NPC function and its peculiarities.
Those attributes are of Collective Macromolecular Interactions (CMI) and we can not get to that area using the same mathematical and physical tools of the one scale narrative.
What are the mathematical models for behavior of macromolecules in an assembly?
If that is the conventional MD for macromolecules, then we can not get the assembly's morphologies (structures) correctly without specifics of protein-to-protein interactions as of the collective entity.
Because the conventional MD uses many just adjusting conjectures and parameters, the basis of MD is questionable, not to mention the macromolecular particles collective interactions.
That was actually one of the reasons why in the present paper (study) authors were not able to satisfy their needs for modeling of macro-assemblies using just the MD.
4) In Fig. 2,a given an incomplete Top-Down hierarchy, whereas the Bottom-Up sequence is in need to be performed for the scaled reconstruction of spatial assembly with reasonable justification.
5) Pretty important is that what is shown, for example, in Fig. 5,b is looking as a craving for attempting to combine protein-to-protein interaction in the vicinity of the Nup84-complex in the NPC which is of high doubt, as long as for the description of the combination and attraction of proteins were used inappropriate tools - yes, what authors could get at their disposal.
And that can be said about any assembly recognized in the work.
6) Authors write in p. 686: "we also need information on the interactions
between nucleoporins. We obtained this information from a large
number of overlay assays and affinity purification experiments, ".
As we see, the data are just of approximate nature -- taken from observation, which in no way is explaining to us -- Why these nucleoporins are sticking to each other with this spatial morphology?
Yes, the number of hypotheses an experienced biologist can produce, but what is the justification for that?
According to conventional orthodox physics - homogeneous, using the adjustable MD, linear local interactions of point particles, traditional many-body (many-point) problem statements and their approximate solutions (even for point particles), etc., etc.?
That means, Fig. 5,b visual version is, well, so far a fiction.
In p. 867 we can find in a figure's caption -- "b, The mutual arrangement of the Nup84-complex-associated proteins as visualized by their localization volumes. The localization volumes, obtained from the final NPC structure (Fig. 9), allow a visual interpretation of the relative proximities of the proteins."
7) It is also interesting to read about what was used in the study to approach for findings of explainable proteins interaction -- the famous protein -- protein (P-P) interaction.
In p. 689 we can read in this regard: " This
composite implies that at least three of the following six possible types of interaction must occur: blue--red, blue--yellow, blue--green, red--green, red--yellow and yellow--green......"
"These considerations can be encoded through a tree-like evaluation of the conditional restraint. At the top level, all optional bead--bead interactions between all protein copies are
clustered by protein types. Each alternative bead interaction is restrained by
a harmonic upper bound on the distance between the beads; these are
`optional restraints', because only a subset is selected for contribution to the
final value of the conditional restraint."
This is the combinatorial mathematics arguments for the physical fields problem. Well, whatever authors had at their disposal - still that is not the protein -- protein interaction especially in a collective mode.
Authors even introduce out of distraction just the statistical value as "protein contacts," p. 690:
"Protein contacts. The proximities of any two proteins in the structure
can be measured by their relative `contact frequency', which is
defined by how often the two proteins contact each other in the
ensemble (Fig. 10b)......"
"Notably, few high-contact frequencies are seen between proteins of the same type, indicating that the NPC is held together primarily by heterotypic interactions."
These descriptions taken from p. 690, fully reveal the available today mathematical approaches to P-P interaction -- which is often straight to the combinatorial study of the possible interactions -- no chemistry, no physics; and the math is from another universe. Regarding the MD application we made few remarks in the above texts for other studies using the MD, generally it is too simplistic tool to be considered up for this task in the cellular biology.
Conclusions to the paper:
1) The outstanding result given in this paper should not divert us from the discussion about the homogeneous tools that were used in the study.
2) Also, the suggested spatial structure of Nuclear Pore Complex (NPC) can not be verified and studied further regarding its function in a nuclear-cytoplasm exchange because of inadequate one scale homogeneous structural molecular biology modeling tools only known to authors.
Well, other authors would find any possibility to encroach into the suggested morphology -- and probably this morphology is close or even the reality.
Nevertheless, its fundamentals would definitely preclude the functional studies of the present assemblies.
3) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media and in the sub-section -
as well as in -
Alber, F., Dokudovskaya, S., Veenhoff, L.M., Zang, W., Kipper, J., Devos, D., Suprapto, A., Karni-Schmidt, O., Williams, R., Chait, B.T., Sali, A., and Rout, M.P., "The Molecular Architecture of the Nuclear Pore Complex," Nature, Vol. 450, 29 Nov., pp. 695- 701, (2007).
In the second publication on the same study authors give readers the figure of formulated structure of the NPC with the obvious need for method(s) that will allow to explain the heterogeneous NPC structure function?
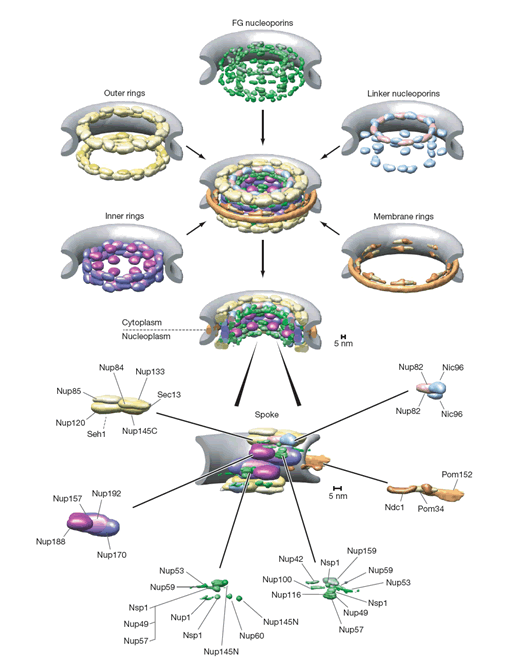
Our Summary:
To this another publication of incredible content, a note regarding the scaling nature of matter under investigation can be said as - that because the structure assembly was recreated by mathematical procedures without the Scaled (3 scales involved, at least) Physical and Mathematical Modeling (SPMM) -- this morphology of NPC in future studies should have the re-evaluation on the basis of at least some kind of SPMM.
The next one publication to review on the subject of polyscaling (multiscaling), is great by its content review with an appeal for tools needed for structural biology - workers should understand and keep in mind.
It's a rather rare situation when the request (a plea) for instrument of need are openly published in spite that the research in this arena is going on for decades!
The paper published is:
Russel, D., Lasker, K., Phillips, J., Schneidman-Duhovny, D., Velazquez- Muriel, J.A., Sali, A., "The Structural Dynamics of Macromolecular Processes," Curr. Opin. Cell. Biol., Vol. 21, pp. 1-12, (2009).
In the p.1 one can find the current state of affaires in the structural biology modeling as well as the recognition that:
"However, none of these computational approaches are always accurate, applicable on all time and size scales of interest, capable of describing all properties of interest, and able to include all available experimental data and theoretical considerations. Such an integrative approach still needs to be developed. "
We won't be talking much on the content other than the following.
In the p.4 a reader can find the outstanding Table 1:
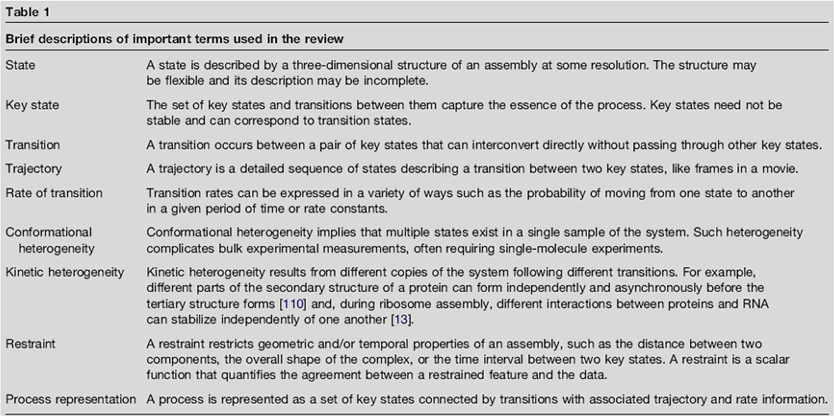
Our comments:
People with sufficient background in math and natural sciences and their history reading this table can suspect that we are in the era of the second part of the XVII century when the need for infinitesimals was evident and Differential Calculus was developed by G.Leibniz and I.Newton.
In other words -- this is the request for a Differential Heterogeneous Scaled (at least two scales) Theory, Governing Equation(s), and actually a Heterogeneous Calculus to study, know, control and to provide the experimental design for the Heterogeneous Scaled (at least two scales) biological system(s) under investigation.
Then following in the paper is the Table 2 with the content that must be commented as long as it says to reader about the methods, techniques used for studying the structures in biology. And this is interesting enough, at least on the side of computational biology - the physical, mathematical weaponry used in this field of biology.
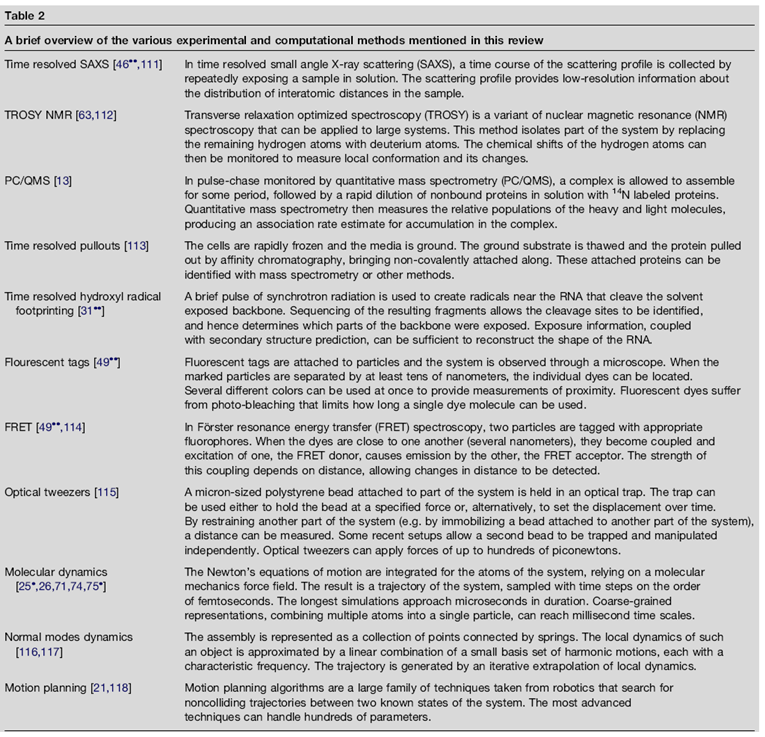
Our comments:
All three mentioned at the bottom of the table mathematical methods - yes, mathematical not biophysical or physical, are incorrect, just simplification of XIX time techniques. There are published studies on that. Which is a fun to watch in comparison to the physical instrument's methods used for experimental studies.
Summary:
1) This is the work of profound professional insight into the set of features that are available right now at one side -- the Homogeneous biomedia characterization and the necessity for those for Heterogeneous Scaled media should be found and developed for a successful study, dynamic modeling of macromolecular assemblies, structures in cellular biology.
The issues drafted in the Table 1, p. 4, are worth commenting specifically.
2) In the Table 1 is given the most striking list of features desired or better saying "dreamed of" for a full scale or complete resolution of "structural dynamics" modeling of cell macromolecular processes.
In the matter of fact, the authors of this paper not knowing the more general point of view have drafted the "wish list" for a thing not less than the "Scaled Heterogeneous Physical and Mathematical Differential Calculus" for the Two-scale (at least) description of transient macromolecular processes in a cell.
3) Thus, we have witnessed the appearance of a pretty rare phenomenon when the need for the theory is so high (strong) that workers created the draft outlined feature -- the table in which the number of the first priority characteristics needed for a process modeling and observation in experiments are being published in a professional journal.
Authors do not know that those features, tools and theoretical fundamentals already have been worked out in the other scientific fields. We would like to mention, that the present days science is the broad endeavor indeed.
4) We would make a few statements related to the points in the Table 1, not for the every point in the table, which is understandable.
In the characteristic wish No. 1 of the table one can find that the desirable feature described as:
"State: A state is described by a three-dimensional structure of an assembly at some resolution. The structure may be flexible and its description may be incomplete."
Meanwhile, in the HSP-VAT language it is the Upper scale formulation of the problem's dependencies for the given "phase" or "species," macromolecular assembly (MA) characteristic state in its phase and spatial manifold.
5) The number two point in the Table 1 reads as:
"Key state: The set of key states and transitions between them capture the essence of the process. Key states need not be stable and can correspond to transition states."
In the HSP-VAT language this is the set of consecutive solutions (values, field's mathematical meanings) of the Upper scale governing equations in the phase field's of the Upper scale physics.
6) The number three point in the table reads as:
"Transition: A transition occurs between a pair of key states that can interconvert directly without passing through other key states."
In the HSP-VAT language this is the transition between the two points on the phase space Upper scale solution curve and these points are obtained in accordance with the HSP-VAT Upper scale governing equations (GE) solutions.
7) For all the other left issues No. 4-9 in the Table 1 (p. 4) the corresponding classifications and exact descriptions and mathematical formulations in the field and language of the HS physics are already existing (have being developed those for more than ~20 years). And that has been applied so far to many sciences, technologies. Among them in this website and other publications are presented:
and other sciences and technologies presented in this website.
Conclusions:
1) It would be nice if authors of the commented up here work
would understand the essence and the implication for their own work and goals
for making effort to implement some tools already existing and suggested to
them according to their own "wish-list" specification via the HSP-VAT that
has been in a public domain so far for a number of years- more than 25
approximately.
2) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media and in the sub-section -
as well as in -
Travkin, V. S. and Bolotina, N.N., "Quantum Chemistry, Physical Chemistry, Molecular Dynamics Simulation, DFT (Density Functional Theory), and Coarse-Graining Techniques Applied in Structural, Cellular Biology, Polymer Science and Implication for Scaleportation," Journal of Alternative Energy and Ecology, No. 2, pp. 58-75, (2011a)
************************************************************************
Kim, W., Tretheway, D.C., and Kohles, S.S., "An Inverse Method for Predicting Tissue-Level Mechanics from Cellular Mechanical Input," J. of Biomechanics, Vol. 42, pp. 395-399, (2009).
A few years ago we tried to deliver to the authors of this particular paper the concepts of Polyscaling and Hierarchy in biomedia. Because their "study" was like about a scaleportation in a biotissue.
That was a vain effort, professors first of all watch their back in terms of employment situation. Then we thought about directly addressing the content of the paper in attempt to analyze - What is Mechanics of cellular media and of "tissue-level" as authors wrote themselves?
Not worth, and better we had published after more then 15 years delay the article - "Principles, Biological and Mathematical Modeling For Elasticity, Poroelasticity of Soft Biomedia, Polymers with Fluids Mechanics in the Bioporous Two-scale Media."
These publications below we think are the good rebuttal to million works on biomedia Continuum Mechanics that have been presented as a Homogeneous media.
Travkin, V. S. and Bolotina, N.N., "Principles, Biological and Mathematical Modeling For Elasticity, Poroelasticity of Soft Biomedia, Polymers with Fluids Mechanics in the Bioporous Two-scale Media," "http://travkin-hspt.com/biophysics/pdf/61BEl-BioHtElasticity-5.1HSPT-f.pdf"
We disassemble here the claims on "multiscaling" coming from the conventional one-scale Homogeneous physics studies published on behalf of the structural, cellular biology topics.
The issue is that the traditional orthodox one-scale-for-all (OSFA) methodologies few years as have been employed as the "multiscale" techniques in biological studies. Following the same move in Nanotechnology applications.
We need to comment on such an "innovative" move in this communal advancement.
As one of the typical studies with the claims regarding the "mutiscaling" used among the methods of research we can comment on the very solid paper:
Arkhipov, A., Yin, Y., and Schulten, K., "Four-Scale Description of Membrane Sculpting by BAR Domains," Biophys. J., Vol. 95, pp. 2806-2821, (2008).
We can read in the ABSTRACT:
"We report a computational study of membrane bending by BAR domains at four levels of resolution, described by
1), all-atom molecular dynamics;
2), residue-based coarse-graining (resolving single amino acids and lipid molecules);
3), shape-based coarse-graining (resolving overall protein and membrane shapes);
and
4), a continuum elastic membrane model. "
In p. 2806 one can read that: "To overcome the limitations of atomistic MD simulations, we utilize coarse-grained modeling and a multiscale approach at four levels of resolution, which allows us to reach timescales up to several microseconds."
In p. 2807 one can read that: "The multiscale approach employed acts at four levels of
resolution: all-atom, single-residue, single-protein, and continuum."
Our Comments:
Here we have again, as in one of the above studies, for the problem with biological media domains with the scales of:
1) the one atom-one residue scale is - ~0.2 nmSc, (Scale spatial);
2) the scale of a single protein -- 1-5 nmSc; which is not walking alone, but imbedded into a polyphase solvent, or docked to other protein(s), or is the part of an assembly;
3) and the scale of constitutive protein complexes - ~10 -- 50 nmSc.
In the same p. 2807 one can read that:
"Our four-level description is based on these models and on our own coarse-graining approaches, which resulted recently in the development of a residue-based CG model (51,57) and a shape-based CG model (52,53). "
In the same p. 2807 one can find the figure caption:
"FIGURE 2 Arrangements of BAR domains studied. The systems studied by simulations are periodic; the simulation box is highlighted as a solid square, and a few periodic images are shown in dimmed color; boundaries of periodic cells are marked by dotted lines. (A) Non-staggered one-row arrangement. (B) Staggered two-row arrangement."
Our Comments:
This figure and the caption show incorrect simulation approach and algorithms. This is the adjusting technique. We are addressing these issues in few sub-sections of this "BIOLOGY..." section.
In the same p. 2807 one can read that:
"For all three levels, MD simulations are performed using NAMD (71).
The fourth level of our description involves a continuum elastic membrane model.
The models, at each level, are parameterized based on properties from the higher-resolution models, as well as from experimental data. "
Our Comments:
Here in the each scale method are used the variety of techniques for simulation - while communication between the models and results done via parameterization "based on
properties from the higher-resolution models," and from some experiments, shows that this is the adjusting or "coupling" of neighboring scales modeling effort.
Meaning, that the data have been brought to some compliance to each other using the adjusting algorithms with specific coefficients, which is the legitimate way to do a scientific investigation - at the same time, it is not at all the Scale Justified Communication.
This is not a Scaleportation, a connection of models and their data via interscale strict mathematical modeling.
This is not a Multiscaling either, the methodology might be named rather as the "multi-resolution" method to simulate the physical task.
Conclusions:
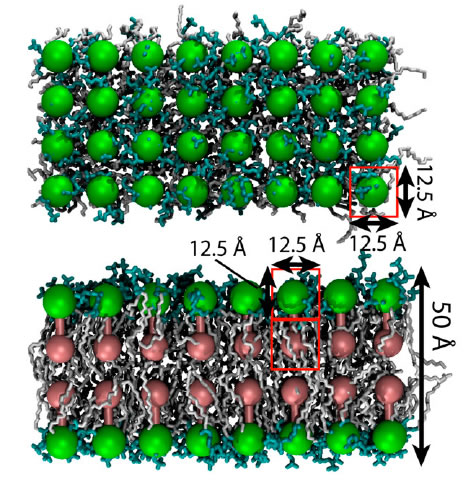
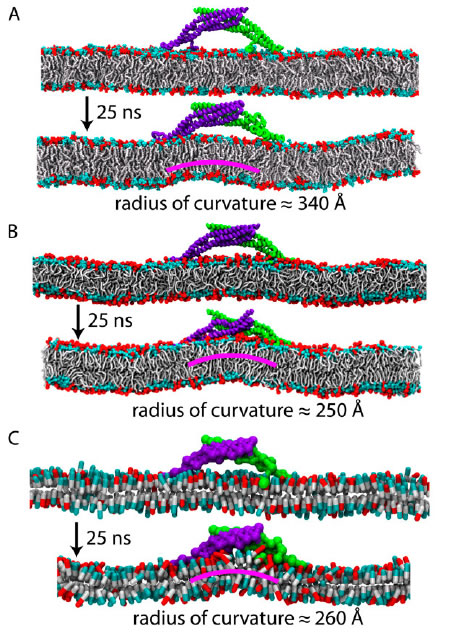
1) In conclusion, that is not touching the subjects of biology itself, to this characteristic "multiscale" study, the modeling methods, as well as the "multiscale" results we would confirm again that all these pseudo-multiscaling techniques, that not using the HSP-VAT methods, can not develop unified, strictly communicating physical and mathematical polyscale models - Do At Least Two Scales, that can show features of Scaleportation, see more in -
2) So, these frivolous algorithms used in computational chemistry, biology, materials science as the "multiscale" ones are in essence the adjusting techniques to make ends meet while using the different scales physics for a one physical problem.
Starting with the Quantum Chemistry simulation.
3) More or less substantial remarks on the Coarse-graining techniques used in Computational, Structural biology, Physical Chemistry, etc. we have placed in the breakdowns of few studies above in this text. Meanwhile, this topic is a large area where people freely using the adjusting techniques with the confidence of fundamental studies, and we discuss further this approximate computational approach.
4) Regarding the implications brought to the Biological Scaled Heterogeneous problem by the variety of conventional Homogeneous physics scale simulation methods, that work "in concert" not via Scaleportation, we will continue to address the issues.
5) We are addressing these and close issues in our sections on Cellular Biology Heterogeneous scaled media and in the sub-section -
as well as in -
************************************************************************
Of course, in our breakdown of biology related traditional tools polyscaled publications we could not avoid addressing the rather mathematical work array.
Again, this is not a specific lab or personalities we select to disassemble the techniques used.
All those selected publications are in the same polyphase, polyscale biomedia areas. Also, the quality of publication played a role, that's it about the selection.
We would talk throughout the multi-issued works regarding the close communication to the above studies, on the paper by -
Zhou, Y.C., Holst, M., and McCammon, J.A., "A Nonlinear Elasticity Model of Macromolecular Conformational Change Induced by Electrostatic Forces," J. Math. Analysis Applic., Vol. 340, Iss. 1, pp. 135-164, (2008).
This paper talk is about the difficult and in some points even not having a
proper developed continuum mechanics theories in relation to, let's take,
two-phase and actually two-scale biomedia which consists of macromolecule
(one) as a polymer nonlinear elastic homogeneous medium with electrical (and
might electrodynamic) constant characteristics, and a solvent with constant
phase electrical characteristics (electrical permittivity) and "The dielectric
constant

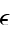 and the modified Debye-Hückel parameter
and the modified Debye-Hückel parameter

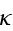 are piecewise constants in domains
are piecewise constants in domains

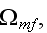

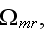

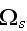 . In particular,
. In particular,

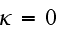 in
in

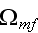 and
and

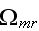 because it models the free mobile ions which appear only in
the solvent region
because it models the free mobile ions which appear only in
the solvent region

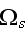 ."
."
There is only one polymer elastic molecule
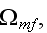 and one rigid molecule
and one rigid molecule
 , meanwhile,
that is supposed to be a lot of both kinds.
, meanwhile,
that is supposed to be a lot of both kinds.
From the ABSTRACT:
"In this paper we propose a nonlinear elasticity model of macromolecular conformational change (deformation) induced by electrostatic forces generated by an implicit solvation model.... "
"The Poisson--Boltzmann equation for the electrostatic potential is analyzed in a domain varying with the elastic deformation of molecules, and a new continuous model of the electrostatic forces is developed to ensure solvability of the nonlinear elasticity equations. We derive the estimates of electrostatic forces corresponding to four types of perturbations to an electrostatic potential field, and establish the existence of an equilibrium configuration using a fixed-point argument, under the assumption that the change in the ionic strength and charges due to the additional molecules causing the deformation are sufficiently small. "
Our Comments:
In fact the problem is not solved - there are given the estimations for numerous separate situations for electrostatic potential without coupled elastic deformation of macromolecule; then given the general result of "Existence of Solutions to the Coupled System." That's it.
Actually the mathematical statement is given as de-coupled, because the body forces in elasticity statement are depending on the potential function solution, but potential is given in equation for already occurred macromolecule elastic deformation? That's the current state of the art.
In p. 136 one can read that:
"This article takes an important step in this direction by describing and analyzing the first mathematical model for the interaction between the nonlinear elastic deformation and the electrostatic potential field of macromolecules."
Our comments:
Because there is no established model for coupling of physics of electrostatic fields (in both macromolecules and a solvent) and elasticity in a system with electrical field dependent deformation of polymer, authors developed the intricate method with the "supposed" change of Poisson-Boltzmann equation to "return" it to the form (which is not supposed to exist, because the taken form of the Poisson--Boltzmann equation is valid for only "while the Poisson-Boltzmann equation (2) holds true for real deformed configurations").
That means authors do not know the electrodynamics GE for a two-phase system with macromolecules and solvent interdependent (interacting) in their dynamics.
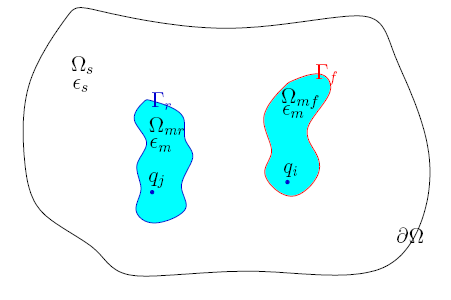
In the initial statement we can read:
"Within the framework of an implicit solvent model which treats the aqueous solvent in s as a structure-less dielectric, the electrostatic potential field of the system is described by the Poisson-Boltzmann equation (PBE)"
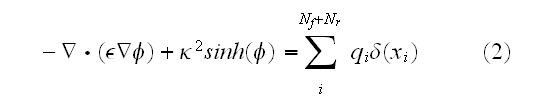
Our comments:
Here in this equation, which is the regular Poisson-Boltzmann equation (PBE) in which we have mixing of the two scales (at least) phenomena:
a) of the atomic scale; and
b) of the continuum media scale - which is not even specified; these two scales are combined with the introduction of the Dirac's function and the Debye-Huckel parameter k.
And this was a conventional thing to do -- in the first half of the XXth century (1923 and up).
Because of the incorrect physical and mathematical initial statements -- in solvent the physics of electrostatics is of the Debye's time (hundred years old), essentially is incorrect;
in macromolecules the physics of electrostatics is incorrect also -- those charged atoms are thousands and thousands within the macromolecules;
plus -- the boundary conditions at the interfaces between the solvent and macromolecules are complex, heterogeneous mostly, the problem's present statement is hardly worth solving. Anyway, it was done. .
Further in the initial statement one can read: ""The finite(large) deformation of molecules is essential to our coupled model, but can not be described by a linear elasticity theory. We therefore describe the displacement vector field u(x) of the flexible molecule mf with a nonlinear elasticity model :
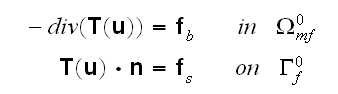
where

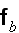 is the body force,
is the body force,

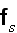 is the surface force and
is the surface force and

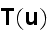 is the second Piola-Kirchhoff stress tensor. "
is the second Piola-Kirchhoff stress tensor. "
Our comments:
As it appears from the further text in this study -- Authors
don't know how to designate, determine the both forces the

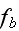 and
and

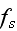 ? And nobody knows exactly -- How to develop Continuum Mechanics constitutive
relations accounting for these forces?
? And nobody knows exactly -- How to develop Continuum Mechanics constitutive
relations accounting for these forces?
And without the designation of both forces the problem is stated as de-coupled, in an incomplete statement. Means can not be solved.
And they can not solve the problem as it appears further from the text.
These

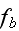 and
and

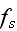 functions should have the well defined form, and the theory should exist on
that, theory or procedure for connection of them to the electrical (and
actually electrodynamic ) fields which existing in all three media presented
in the problem -- both types of macromolecules and the solvent.
functions should have the well defined form, and the theory should exist on
that, theory or procedure for connection of them to the electrical (and
actually electrodynamic ) fields which existing in all three media presented
in the problem -- both types of macromolecules and the solvent.
Authors appeared to develop some substitutive model going via the assessment of the electrostatic energy of the system with necessity to approximate the Lower scale (atomic and sub-atomic) singularities in the body force density that is modeled by a Gaussian function; and with the application of the infinitesimal displacement h of the molecular surface in its out normal direction.
At the end of this study one can read:
"The coupling of elastic deformation to the electrostatic field is of great importance in modeling the conformational change in large macromolecules.
To put this into perspective, more comprehensive and realistic continuum models for macromolecular conformational changes can be developed based on the results in this article, for example, by coupling the (stochastic) hydrodynamic forces from the Stokes or Navier-Stokes equation, or including van der Waals forces between closely positioned molecules."
Our comments:
First of all, the hydrodynamic forces act on the
molecules from outside (externally) and they are not stochastic, also
the macromolecules - solvent system is on its own has the pretty
complicated Scaled (two scales at least) HSP-VAT description,
to which a large
pieces of theory are devoted in this website.
Secondly - van der Waals forces and the elasticity theory for a
heterogeneous medium of macromolecules and a solvent are the different
subjects - and well, are of the scaled nature anyway.
Also - " A major concern in applying these coupled models, however, is the determination of the elasticity properties of macromolecules within the continuum framework, which requires new theoretical models and quantitative comparisons between the continuum modeling and the classical molecular dynamical simulation and/or experiential measurements."
Our comments:
The classical molecular dynamics won't save. It is the mantra people not resting to reiterate are seeking the savior actions from some "More Powerful and Clever then us," neighboring physics field. Like the Continuum Mechanics for Construction Engineers, Chemistry for Chemical Technology, Physics for everything that moves, Atomic physics for Continuum Mechanics, Particle Physics for Atomic physics, String theory for Particle physics, Higgs boson for Large Hadronic Collider (LHC), well, what will help the string theory and LHC?
The chances it will fail to deliver the goal proclaimed are high. Who or What will help in this case?
Of course, the MD will not help -- we spoke on the reasons in many spots above in the text. Yes, people will continue to use MD, meanwhile the development of the other MD - the Heterogeneous Scaled (HS) MD is the urgent issue.
The chances are coming from inside -- because these are the problems of a few scales.
So, we do have a concern and an effort for the polyscaling of elasticity and electrodynamics in structural and cellular biology.
In Conclusion to this study:
1) This is just another situation to confirm that the
protein, macromolecules conformation problem is not going to be resolved by
taking chance to develop one more one-scale coefficient dependent theory.
Because the correct way is to recognize that the Lower scale -- atomic scale
physical phenomena in polymer solution have a major impact onto the
conformation and consequently on the continuum elasticity of macromolecules.
So, the efficiently counted impacts are of the continuum mechanics scales -
that the Bottom-Up / Top-Down Scaleportations need to be tackled no matter what.
That will give the base for constitutive multiphysics macrodependencies which
appear naturally.
2) It was noted for many instances that -- as soon as we can see or understand that in the same volume act few different forces, effects, etc. we immediately should be concerned that this description means -- that the different carriers (phases) in the same volume (or sub-volumes -- also the same) are functioning or acting on behalf of different physical phenomena.
That also means -- that we can freely designate the different phases to be the carriers of their respected physical effects -- firstly, and those effects should be the subject of the appropriate heterogeneous scaled dynamics and static GE -- the secondly. Yes, it is.
3) We are addressing these and close issues in our
sections on Heterogeneous scaled media elasticity theory and in the
sub-section -
as well as in -
**************************************************************************
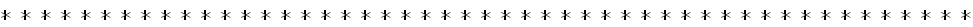
Within the huge field of Bacteriology had grown the understanding and the acceptance of point of view that the proper description of bacteria interacting within the colony, with the environment and other species and tissues should be considered as the heterogeneous subjects (agents) acting and developing as the separate entities. Starting with this point of view it is still a long way to understanding of the not only single chemical mechanisms of interaction, but and inclusive other phenomena described by the heterogeneous scaled physics of bacterial colonies.
The following brief analysis of the study
Be'er, A., Zhang, H.P., Florina, E.-L., Payneb, S.M., Ben-Jacob, E., and Swinney, H.L., "Deadly Competition Between Sibling Bacterial Colonies," Proc. NAS USA, Vol. 106, No. 2, pp. 428-433, (2009)
might be viewed as reflecting on the substantial portion of works in microbiology when the experimental facts speak in a favor of heterogeneous and two-scale morpho- and biogenesis in microbial populace, but the tools explored for research are not adequate to the tasks of this complexity and workers use the same known to them homogeneous physics, chemistry and mathematics instruments.
From the Abstract:
"Bacteria can secrete a wide array of antibacterial compounds when competing with other bacteria for the same resources. Some of these compounds, such as bacteriocins, can affect bacteria of similar or closely related strains. In some cases, these secretions have been found to kill sibling cells that belong to the same colony. Here, we present experimental observations of competition between 2 sibling colonies of Paenibacillus dendritiformis grown on a low-nutrient agar gel. We find that neighboring colonies (growing from droplet inoculation) mutually inhibit growth through secretions that become lethal if the level exceeds a well-defined threshold....."
Our Comments:
Here one reads on pure heterogeneous mechanisms of interaction within a colony and between the colonies.
Authors write further that bacteria are not a single living organism that is acting on its own only. Tremendous amount of findings lead researchers to understanding and acceptance of the concept that the bacteria when in a colony behave in a dramatically different way - while demonstrating the collective process features.
They act in cooperation with each other, that is why they develop the different spatial structures - spatiotemporal patters in reflection to the environment setting.
A few pictures from the study clearly show the polyscale nature of the bacteria colony in action.
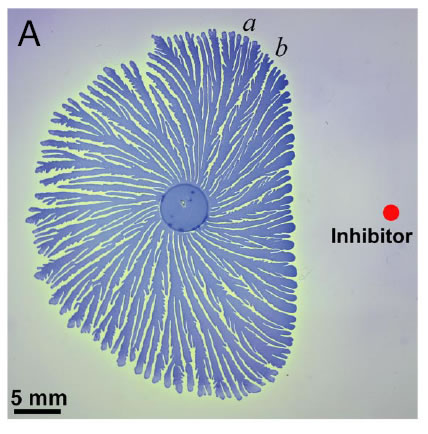
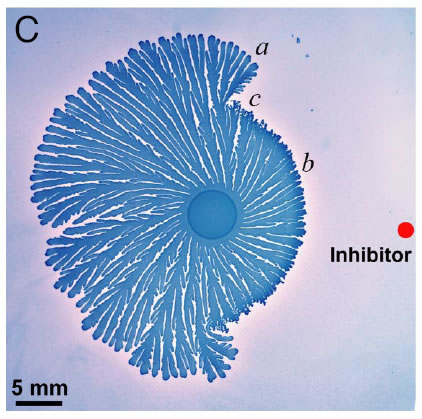
Our Comments:
In page 431 authors suggesting the diffusion-reaction type modeling equation for colonies growth and interaction.
This modeling equation is inappropriate for these heterogeneous processes absolutely, due to few (many) reasons:
1) It is not describing properly the transport in the nutrition solvent area (region) as a result of a few grounds as the macromolecules transport (it's not a diffusion by at large), convectional media partition included, not the all physical phenomena included;
2) It is not unfolding properly the diffusion in the growth areas - neither in the liquid sub-volume nor in the aggregated bacteria volumes (phases);
3) The equation itself is incorrect in the heterogeneous areas of bacteria growth.
Heterogeneous Summary to this study:
1) We are extremely pleased that more and more evidences have been recorded in last decades supporting the theoretical conceptions of polyScale Heterogeneous Bacteriology (BHS). The matter of fact is that the BHS is not just a verbal statement, assurance, point of view. The thing is that we support the statement of BHS with the physical and mathematical models, governing equations (GE), methods of solving these two scales at least models and GE, numerical and analytical simulations and results.
2) Recent methodical proofs of at least three scale, above the cell structure, those are - (1) single bacterium scale - ; (2) scale of fingers (branches); (3) scale of the colony; four-phase (bacteria; nutrition solvent; signaling factor - inhibitor; bacteria intercellular communicator (exchange) factor of chemical nature only), that are participating in the transient colony expansion, call for the poly-phase heterogeneous representation of bacterial media and factors acting in morphogenesis.
3) We are addressing these and close issues in our texts on Heterogeneous polyScale Bacteriology in the sub-section -
In generally the very useful review paper by
Grassi, M. and Grassi, G., "Mathematical Modelling and Controlled Drug Delivery: Matrix Systems," Current Drug Delivery, Vol. 2, No. 1, pp. 97-116, (2005);
nevertheless, there have been written many questionable points regarding the physical presentation and mathematical modeling in the Drug Delivery field. We are talking, of course, about the scales in the drug and the scales of human body drug administered environment.
From the Abstract:
"This paper deals with the physical and mathematical modelling description of drug release from matrix systems. In the introduction, matrix systems are considered in the wide frame of the controlled release systems and the concept of mathematical model is briefly discussed......"
".....This review points out the fact that the comprehension of the phenomena ruling drug release from matrix systems is appropriate from both the physical and modelling point of view, although further improvements are always possible and desirable."
Our comments:
It might be of no big problem in drug delivery from the point of view of a medical practitioner or drug developer with the chemistry education and medical conventional profession understanding - and that was in the past. May be!
From now on - when the exact and on target drug delivery to the subject of selected cells or even smaller scale within the cell is on the Task list - we need to see this field as the one of great practical importance.
And there is no way the contemporary homogeneous physics and mathematical simulation allow to reconsider the problem with drug delivery on these scales - micro - and nanometer and to the selected cells and within those selected group of cells. No Way - these tools are not up to the task..
Summary:
There are a lot of homogeneous physics statements in the review and all related to Heterogeneous subject matters. Nevertheless, we found interesting to comment on understanding within this separate group of researchers of polyphase, polyscale medium presentations within the known mathematical background.
1) The quality of models - and consequently, the quality of Controlled drug Release Systems (CRS) can be dramatically improved when the multiphase media for drug tablets and release environment to be adopted and accepted as the most reasonable for physical and mathematical modeling.
Thus, the modeling concepts and predictability (quality) of models can be significantly improved in comparison to models (19) - (30), and (33)-(41).
2) The medium of drug release should be included into consideration and modeling. This is not even the issue at present time! What is the tissue the drug in? What is the pathway the drug has gone along?
3) The multiphase approach should be accepted as for the drug content volume (matrix) as well as for the impact tissue.
4) When the polyphase, multiscale media and processes in a human tissue to be used in the drug delivery scenarious, then and only then the trust of industry might get to the sufficiently high level when these predictive tools to be used in preparation and procedures utilized for the treatment by physicians.
as well as in -
In conclusion of these partial (will be continued) analytical notes it will be appropriate to mention here that we also did communications as of the similar content as the above remarks posed here to many of authors of the reviewed above papers. That is, they know what is in their work-studies.
Alber, F., Dokudovskaya, S., Veenhoff, L.M., Zang, W., Kipper, J., Devos, D., Suprapto, A., Karni-Schmidt, O., Williams, R., Chait, B.T., Rout, M.P., and Sali, A., " Determining the Architectures of Macromolecular Assemblies," Nature, Vol. 450, 29 Nov., pp. 683 - 694, (2007).
Alber, F., Dokudovskaya, S., Veenhoff, L.M., Zang, W., Kipper, J., Devos, D., Suprapto, A., Karni-Schmidt, O., Williams, R., Chait, B.T., Sali, A., and Rout, M.P., "The Molecular Architecture of the Nuclear Pore Complex," Nature, Vol. 450, 29 Nov., pp. 695- 701, (2007).
Arkhipov, A., Yin, Y., and Schulten, K., �Four-Scale Description of Membrane Sculpting by BAR Domains,� Biophys. J., Vol. 95, pp. 2806-2821, (2008).
Be'er, A., Zhang, H.P., Florina, E.-L., Payneb, S.M., Ben-Jacob, E., and Swinney, H.L., "Deadly Competition Between Sibling Bacterial Colonies," Proc. NAS USA, Vol. 106, No. 2, pp. 428-433, (2009).
Deem, Michael W., "Mathematical Adventures in Biology," Physics Today, Vol. 60, Iss. 1, pp. 42-47, (2007).
Doubrovinski, K. and Kruse, K., "Cytoskeletal waves in the absence of molecular motors," Europhysics Letters, Vol. 83, pp. 18003-p1- 18003-p6, (2008).
Joanny, J.F., Julicher. F., Kruse, K., and Prost, J., `Hydrodynamic theory for multi-component active polar gels," New Journal of Physics, Vol. 9, pp. 422-(422-17), (2007).
Grassi, M. and Grassi, G., "Mathematical Modelling and Controlled Drug Delivery: Matrix Systems," Current Drug Delivery, Vol. 2, No. 1, pp. 97-116, (2005).
Günther, S. and Kruse, K., "Spontaneous Waves in Muscle Fibres," New Journal of Physics, Vol. 9, pp. 417- 430(417+13), (2007).
Kim, W., Tretheway, D.C., and Kohles, S.S., "An Inverse Method for Predicting Tissue-Level Mechanics from Cellular Mechanical Input," J. of Biomechanics, Vol. 42, pp. 395-399, (2009).
Liao, S., Chan, C.K., and Ramakrishna, S., "Biomimetic Nanocomposites for Tissue Engineering," J. Bionanoscience, Vol. 1, No. 1, pp. 1-13(13), (2007).
Newman, T. J., "Modeling Multicellular Systems Using Subcellular Elements," Mathematical Biosciences and Engineering, Vol. 2, No. 3, pp. 611-622, (2005).
Newman, T.J. and Grima, R., "Many-body theory of chemotactic cell-cell interactions," Phys. Rev. E, Vol.70, pp. 051916 +15, (2004).
Russel, D., Lasker, K., Phillips, J., Schneidman-Duhovny, D., Velazquez- Muriel, J.A., Sali, A., "The Structural Dynamics of Macromolecular Complexes," Curr. Opin. Cell. Biol., Vol. 21, pp. 1-12, (2009).
Sandersius, S. A. and Newman, T. J., "Modeling Cell Rheology with the Subcellular Element Model," Physical Biology, Vol. 5, pp.015002- , (2008).
West, Geoffrey B. and Brown, James H., "Life's Universal Scaling Laws," Physics Today, Vol. 57, Issue 9, pp. 36-42, (2004).
Zhou, Y.C., Holst, M., and McCammon, J.A., "A nonlinear elasticity model of macromolecular conformational change induced by electrostatic forces," J. Math. Analysis Applic., Vol. 340, Iss. 1, pp. 135-164, (2008).

![]()