AES_M4:

Travkin HSPT

Hierarchical Multiphase Muscle Blood System Simulation

NIH Proposal of 1994

Project Summary:

The project is aimed at finding the real, physically grounded way to model and simulate the transport of a multiphase healthy blood medium in a muscle tissue blood vessel network. Since no one model exists at the present time that could account for multiscaling and consider actual blood vessels morphology, the suggested development will treat the blood flow in four scale heterogeneous systems, including: 1- separate cells (red and white) and dispersed cell medium modeling as well as capillary and arteriole wall scale modeling; 2 - single blood vessel models including previous multiphase scale governing equation statements; 3 - single muscle fiber capillary network scale modeling; 4 - finally the three phase blood transport modeling in muscle fiber bundle capillary network. To create these kinds of models the nonlinear multiscale morphological modeling approach that has been developing by the principal investigator must be used and significantly improved. Modeling procedures, it is believed, will provide more accurate and physical model output while considering the transport of blood constituents on each level of the hierarchy. After being developed, these models would be significantly advantageous in comparison with existing one-phase-one-vessel models, due to their multilevel description and direct dependence on given specific muscle morphology. Suggested achievements should bring the biomechanical science of blood circulation modeling on the next level of knowledge and understanding.

TABLE OF CONTENTS

1. PHASE 1 RESEARCH PLAN ..................................................................................... 6

1.1. Specific Aims............................................................................................ 6

1.2. Significance............................................................................................. 6

1.2.1. Short Review of Existing Models in Blood Flow Modeling and

Specifically in Muscle Blood Supply System Modeling............................ 6

1.2.2. New Methodology to be Applied to the Muscle Blood Supply

System Modeling........................................................................... 7

1.3. Relevant Experience .................................................................................. 8

1.4. Theoretical Methods and Numerical Experimentations ....................................... 9

1.4.1. Multiphase Blood System Modeling of Red, White Cells as Corpuscles and

Non-Newtonian Blood Plasma 9

1.4.2. The Arteriole and Capillary Blood Vessel Walls Level ............................ 12

1.4.3. Single Capillary or Arteriole Blood Stream Multiphase Modeling .............. 13

1.4.4. Development of Muscle Fiber Capillary Network Basic Element List......... 14

1.4.5. Muscle Fiber Capillary Network Simulation ......................................... 15

1.4.6. Simulation of the Major Role of Blood Capillary, Arteriole and Venule Flow

Network in the Muscle Fiber Bundle 18

1.4.7. Conclusions ................................................................................ 19

1.5. Literature Cited ....................................................................................... 19

1. PHASE 1 RESEARCH PLAN

1 SPECIFIC AIMS

At present time, blood system circulation modeling has no development of even a one-vessel (on an arterial level as well as on a capillary level) comprehensive correct biomechanical system simulation. The lack of corresponding theory is the evident cause of the situation. The aims of the current work are to develop a hierarchical multiphase system to model and research the flow of a three-phase blood medium in the network of a single straight muscle fiber bundle. This comprehensive approach at the I-st and II-nd Phase development will include in the modeling system all of the major biomechanical multiphase phenomena, except deformability and movement of the vessel walls' soft tissue and mechanical control of the given part of circulation system. Mathematical modeling of physical processes occurring in strongly heterogeneous media results on the whole in the necessity for medium characteristics development, and accordingly, for process equations.

The first level of consideration is a separate cell (red and white) and dispersed cell medium flow modeling in the plasma constituents. Also the first level of consideration is modeling of phenomena in the capillary or arteriole wall as a permeable and morphologically complex 3-phase structure entity.

The second hierarchical level includes the processes of mass and momentum multiphase transport in a single blood vessel.

At the third level, the scope of problems extends toward the lowest level of the capillary network around a single muscle fiber. Among the processes involved for consideration, are the processes of gas exchange mechanisms and blood cell permeation and transformation during the course in the blood fiber network.

The fourth level represents the kind of problem which describes the transport of blood in the blood vessel network of a separate muscle fiber bundle. This includes consideration of all lower levels of the hierarchy - combining them into a complex specific spatial structure which has no analogy among the non-living natural and engineering systems.

Development of the new integro-differential transport equations in the heterogeneous ( and living) media and an application of non-classical equation types, are being considered as the present agenda in this application. Whereas, in many cases, quasihomogeneous and quasistochastic approaches used almost exclusively now are not sufficient for description of the physical process peculiarities in the heterogeneous media and especially in living systems. Those systems are often quite nonlinear and sensitive to disturbances of any kind. Among major aims of the application are the following:

1) Provide theoretical derivation of main sets of governing equations (GE) on each level of the hierarchy and estimate feasibility of closure developments.

2) Develop theoretical mechanisms and varieties of closure approaches for each specific blood system hierarchical level.

3) Estimate the feasibility of theoretical procedures for the development of numerical convergent algorithms for solution evaluations of the equations governing transport.

1.2.1 Some of Existing Models in Blood Flow Modeling and Specifically in Muscle Blood

Supply System Modeling

The proposed research will conduct development and computer simulation of practically all of the dominant circulation mechanisms of the muscle blood supply system (MBSS) comprising the main objective of the Phase II. These achievements primarily will give the ability to simulate and investigate the critical phenomena of muscle functioning and provide the researches with the important tool. The targeted product of Phase II is the theoretical models and computer software that will be capable of attracting additional funding for further development of commercial software to benefit the medical industry.

The muscle blood circulation modeling equation forms can be very different. The parabolic, hyperbolic or integro-differential kind of equations allowed, liner or nonlinear - because the assumptions and initial assumed depth of considered physico-chemical phenomena can vary. The types of transport equations usually applied for blood flow modeling are incorrect in accounting for many important features.

The flow of blood matter as three-phase heterogeneous multidispersed media with extremely intricate white cell behavior has not been attempted to be explained and implemented in correct mathematical forms. Research usually takes the most important features as, for example, erythrocyte aggregation kinetics (Deng et al., 1994; Shehada et al., 1994), or non-Newtonian viscosity of the blood taken as a whole fluid (Perktold et al., 1989; Sagayamary and Devanathan, 1989; Thurston, 1972, 1994), or erythrocyte sedimentation (Kuo et al., 1994; Oka, 1983, 1985 ) and etc.

The blood vessel's wall structural complexity only recently got attention in constructing constitutive relations see, for example, Humphrey et al. (1989). The authors admit that "there has been no attempt to quantify the possible heterogeneity within a layer of the wall, and this seems extremely difficult at present." The nonhomogeneity of a blood vessel's form is being studied primarily from the point of view of fundamental understanding of arterial stenosis, Sagayamary and Devanathan (1989), Young (1979).

The modeling of network morphologies in the blood supply system is actually constrained due to the shortage or absence of applicable methodologies and approaches. The effects of blood stream division or bifurcation being investigated use almost no knowledge base from large information background accumulated in mechanical engineering (Matsuo et al., 1989; Pinchak and Ostrich, 1976).

1.2.2 Methodology Applicable for the Muscle Blood Supply System Modeling

There are four basic theories are usually admitted to derive transport equations for heterogeneous media: 1) averaging theories, 2) stochastic approaches, 3) homogenization theories and 4) classical continuum theories (approaches). Meanwhile, an interception of above theories might be found in several theories. To obtain averaged equations and model or medium characteristics, different methods are being applied for periodic or almost periodic microstructures, porous media and media with two- and three phase movement. Depending on the investigated problem's peculiarities, goals and problem statements either the quasihomogeneous approach or a stochastic interpretation of it could be applied. The later could be called in analogy, a quasistochastic one. The entire essence of quasihomogeneous approach results in getting effective transport coefficients for deterministic classical equations of mathematical physics.

A problem formulation in a quasistochastic statement has parameters characterizing medium properties, considered as stochastic quantities or stochastic coordinate functions. These functions are assumed to be known or assigned, and because of this the problem solution, depending on medium stochastic characteristics, will have stochastic character as well. Determination or calculation of effective parameters for equations is usually based on some medium morphology model and could count tens of methods for quasihomogeneous and quasistochastic approaches.

Meanwhile, the strict mathematical averaging theory has been sufficiently developed mainly for classical differential equations of mathematical physics. That means, first of all, that those used now like the second order equations are taken without junior terms or for the cases, when their influence is insignificant.

At the same time, the new heterogeneous theory started by Whitaker, Slattery, Gray, and others in 1967 allow the description of transport processes in a heterogeneous media much more precisely and definitely. There are few applications, which have practically benefited from these theoretical achievements. At present proposal the new approach is being presented.

The current application has the intention for developing the multiscale muscle blood supply system models (MBSSM) on the basis of the latest results obtained in heterogeneous media transport theory.

1.4.1. Multiphase Blood System Modeling of Red, White Cells as Corpuscles and Non-Newtonian Blood Plasma

The deformable, soft substance of red and white cells represents a very distinct kind of modeling problem comparing to the conveniently understood two-three phase flow phenomena. Further, the nonlinear, non-Newtonian continuous fluid of the plasma should dictate a quite different approach to model development, Fig. 1. How influential nonlinear medium characteristics would be on the transport characteristics might be shown in the next example, more related to blood plasma momentum transport description. ………..

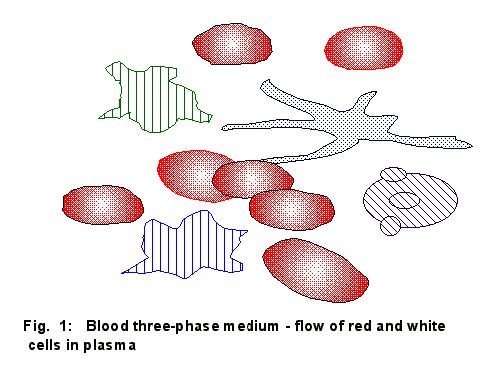
Many different phenomena of blood rheological properties including non-Newtonian viscosity are directly outlined by the multiphase nature of the substance. However, there is no correct models exist to treat a blood medium with the whole extent of it's major feature, see Thurston (1972, 1994), Deng et al. (1994), Oka (1983, 1985), Schmid-Schonbein (1987). Among many quite unusual properties, the movement and form changing of the white blood cells expose an outstanding difficulty for mathematical description. Despite a smaller volume fracture, the influence of white blood cells on blood rheology is significant, Chien et al. (1983), Bagge et al. (1980), Schmid-Schonbein (1987). The multiphase medium of blood cells and nonlinear blood plasma fluid will be treated as an actual 3-phase medium with the specific peculiarities of white cells.

1.4.2. The Arteriole and Capillary Blood Vessel Walls Level

A very complicated feature of internal blood vessel transport is the multiphase layer medium near the vessel's wall, Fig. 2. Thus, the flow over the rough surface of endothelial cells (Sato and Ohshima, 1994; Worthen et al. 1987), plus the larger objects with independent determinism, assigned partially by external mechanisms (meaning with no close or directly related affiliation) and partially induced by current near-neighborhood interrelations with determined functions of vessel's morphology see, for example, Gallik et al. (1989), Goetz et al. (1994), Harlan (1985) constitute few of the difficulties. These objects are leukocytes, stenosis, other defects and structured heterogeneities of blood vessel's wall. Mechanisms developed in works by the principal investigator will allow to deal with these morphology phenomena.

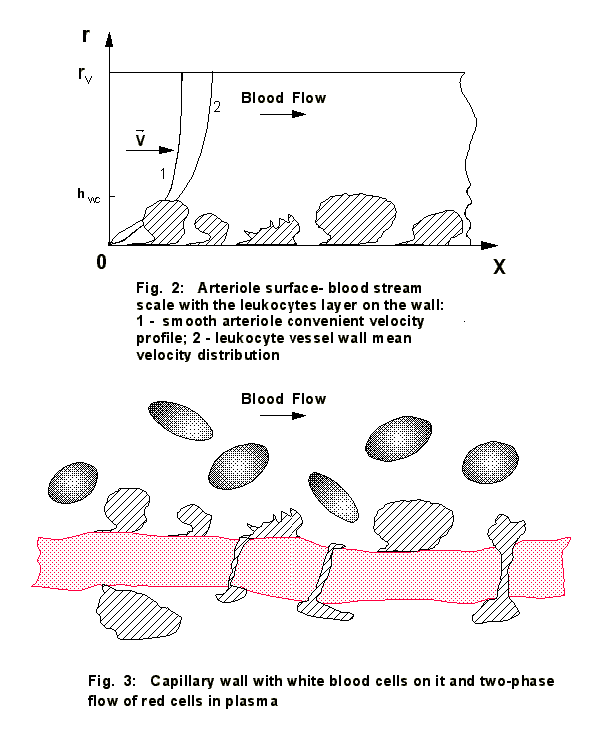
The size of blood vessels and their wall's internal structure are determinant issues for the blood constituents and nutrients transport through the vessel walls, see Figs. 3, 4. Nevertheless, in the approach by Humphrey et al. (1989), which is rather comprehensive (still incorrect) it is admitted that "although the intima plays an important role as a blood-vessel interface, it is probably not structurally significant.... and will not be considered further".

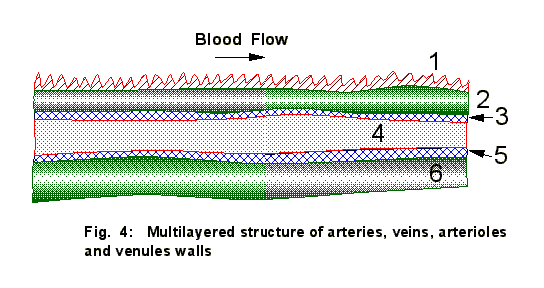
Modeling of two main transport mechanisms through the capillary wall: literally diffusion of nutrient constituents and active transport through the diapedesis of white cells is the challenging problem due to an unusual combination of relatively well known physical mechanism and still unknown and un-simulated physical phenomena of deformable white cell transport through the vessel's wall.

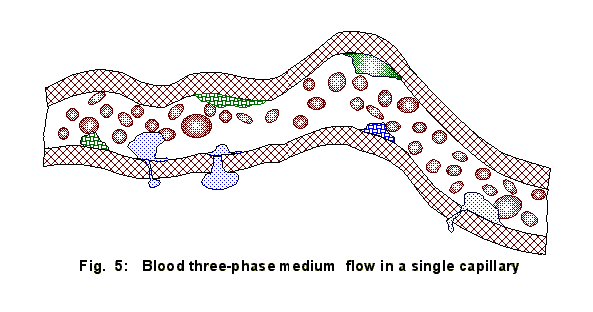
1.4.3. Single Capillary or Arteriole Blood Vessel Multiphase Modeling

Considering a heat- and mass transport mathematical modeling in a separate blood vessel medium, Figs. 4, 5, the equations of mass balances and heat transfer usually can be derived from the following forms of the equations

valid for process description in a separately taken element (capillary) of a given heterogeneous media Fig. 5, - the blood circulation network. The boundary conditions at the blood-wall interphase would be

where r_s – function corresponding to the transformation, penetration or reaction rate on the unit surface, n₁ - normal vector to the interphase surface. The absence of reaction leads to the interface flux, assigned or dependent on some functions

The real transport conditions on the vessel wall need to be depicted in quite different forms of the boundary equations, which will be a topic of awareness in the proposed study.

The complexity of blood flow in a capillary seen in Fig. 5, where a multidisperse self-organizing blood medium moves through the highly non-homogeneous channel with stochastic obstacles on the channel’s wall.

Among the main problems encountered on that level of hierarchy are:

a) Modeling of three-phase (red, white cells and plasma) blood medium momentum transport in blood vessels;

b) Non-smooth irregular channel walls with moving living obstacles on them;

c) Irregular shape and longitudinal curvature of separate blood vessel;

d) Evaluation of the assumptions due to non-Newtonian approximation of flow phenomena for the 3-phase blood medium.

Justifying the choice of calculation formulae used to determine the transfer parameters is important and difficult. Various erroneous positions are shown to exist in the literature for determining transfer parameters, i.e., equating the errors of the calculation formulae to the error of obtaining transfer parameters; using integral values of the sought field to find significantly varying transport parameters, etc.

There is shortage of developed methods for finding out the effective one-concentration ( one-temperature) coefficients for mathematical models with the variable or nonlinear coefficients and more of that, with additional integro-differential terms in two- and three-phase statements. The biggest challenging problems here are the consistent lack of new equations understanding and insufficient development of closure theory, especially for integro-differential equations.

In the suggested study the correct equations for three-phase blood medium transport will be developed and the differences with the most often adopted non-Newtonian blood models estimated.

1.4.4. Muscle Fiber Capillary Network Basic Element List

The morphology of a MBSS capillary network features the infinite set of varieties of junctions and branches, see Fig. 6. The problem in this situation is to develop morphological classification and description of basic key morphological elements. Some information on hydrodynamics and resistance coefficients of arterial branching had been developed in series of works, for example, by Pinchak and Ostrich (1976), Matsuo et al. (1989). Then the developed database specific elements will be used in the theoretical development of closure models, procedures and algorithms. That will be one of the key points in the successful closure of complex additional terms in the governing equations.

1.4.5. Muscle Fiber Capillary Network Simulation

…………

…………The non-Darcian effects usually considered are the no-slip and the inertia effects. These effects normally decrease the flow and heat transfer rates while consideration of the porous medium nonhomogeneity enhance the mass transfer. In the commonly accepted equation of momentum, all kinds of nonlinearities in resistance, convective and diffusive phenomena included are in the Darcy resistance term

Almost always in porous medium modeling the diffusion term ( Brinkman term) in the momentum equation is dropped

usually turning out to be significant near interphase boundaries. What is much more interesting, that this term should be sufficiently influential near inner boundaries between two heterogeneous structures. What concerns the flow resistance terms of the first ( Darcian drag term) and second power (called the Forchheimer term)

then, as shown in works of Travkin and Catton (1992 a,b,c) is that all of the forms of the Darcy term as well as the quadratic term depend directly on the assumed version of the convective and diffusion terms, while the second and more important thing is that both diffusion (Brinkman) and drag resistance terms in the final forms of the flow equations are all directly connected together.

Meanwhile, the Darcy's law becomes inadequate, which is shown and in other works, when the flow Reynolds number based on the mean pore diameter is of the order of one or greater, due to the fact that the inertia force is no longer negligible in comparison to the viscous effect. Most non-Darcian studies are based on a model summarized by the equation

where b is a constant, determined either experimentally or analytically, and U is the Darcian velocity.

Meanwhile, the correct transport equations in heterogeneous 2 scale blood capillary network look very different. The 1-D momentum equation in the direction along the longitudinal x axis, Fig. 6, with detailed description of the medium morphology can be depicted as follows

where the sign ^ means fluctuation of velocity ( and further, others variables ) inside of the representative volume. The next example is the generalized longitudinal 1-D mass transport equation of non-linear blood constituent fluid in the capillary network phase, including description of potential morpho-fluctuation influences, for a medium morphology with only 1‑D fluctuations it can be written in 2-scale morphology as follows

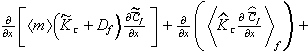
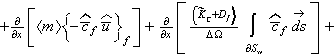
while the corresponding mass transport equation in the heterogeneous tissue of fiber and vessel's wall (motionless) phase might be simplified

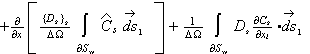
There are usually from 2 to 4 terms in each of the equations that need to be modeled. The morphology of the blood capillary network governs closure of these very influential and difficult to implement nonlinear terms. The modeling of two-medium, namely blood capillary network medium and muscle tissue medium, mass transfer exchange phenomena, of course, should not be limited and tied by the Fick's law shortcomings - Wheatley and Malone (1993). Development of the third scale capillary network governing equations along with the closure modeling technique will be the aim of that step in the research.

1.4.6. Simulation of Major Role of Blood Capillary, Arteriole and Venule Flow Network in the Muscle Fiber Bundle

More complex problems arise while describing the flow in the more highly structured heterogeneous medium, such as the muscle capillary bundle shown on Fig. 7.

…………………

……… The fourth scale modeling achievements for MBSS include derivation of the governing equation set, identifying the specific goals for the muscle bundle capillary network simulation, procedures to reach them, and development of modeling algorithms and software. Also the subsequent set of complementary experimental work to promote the estimation of models validity will be formulated.

1.4.7. SUMMARY

……………………………………

1.5. BIBLIOGRAPHY

Bagge, U., Amundsson, B., and Lauritzen, C., (1980), "White blood cell deformability and plugging of skeletal muscle capillaries in hemorrhagic shock", Acta Physiol. Scand., Vol. 108, pp. 159-163.

Bayliss, L.H., (1959), "Axial Drift of Red Cells When Blood Flows in Narrow Tube", J. Physiol., Vol. 149, pp. 593-613.

Chien, S., Schmalzer, E.A., Lee, M.M.L., Impelluso, T., and Skalak, R., (1983), "Role of White Blood Cells in Filtration of Blood Cell Suspensions", Biorheology, Vol. 20, pp. 11-28.

Cowin, S.C., (1974), "The Theory of Polar Fluids", Adv. Appl. Mech., Vol. 14, pp. 279-347.

Crapiste, G. H., Rotstein, E. and Whitaker, S. (1986), "A General Closure Scheme for the Method of Volume Averaging", Chem. Engin. Scien., Vol. 41, No. 2, pp. 227-235.

Deng, L.H., Barbenel, J.C., and Lowe, G.D.O., (1994), "Influence of Hematocrit on Erythrocyte Aggregation Kinetics for Suspensions of Red Blood Cells in Autologous Plasma", Biorheology, Vol. 31, pp. 193-205.

Dybbs, A., Edwards, R. V. (1982), "A New Look at Porous Media Fluid Mechanics ‑ Darcy to Turbulent," Proceedings of the NATO Advanced Study Institution on Mechanics of Fluids in Porous Media, Newark, Delaware, July 18-27, NATO ASI Series E, No. 82, pp. 201‑256.

Fand, R. M., Thinakaran, R., 1990, "The Influence of the Wall on Flow Through Pipes Packed with Spheres," ASME Journal of Fluids Engineering, Vol. 112, No. 1, pp. 84‑88.

Gallik, S., Usami, S., Jan, K.-M., and Chien, S., (1989), "Shear Stress-Induced Detachment of Human Polymorphonuclear Leukocytes From Endothelial Cell Monolayers", Biorheology, Vol. 26, pp. 823-834.

Goetz, D.J., El-Sabban, M.E., Pauli, B.U., and Hammer, D.A., (1994), "Dynamics of Neutrophil Rolling over Stimulated Endothelium in Vitro", Biophys. J., Vol. 66, pp. 2202-2209.

Harlan, J.M., (1985), "Leukocyte-Endothelial Interactions", Blood, Vol. 65, pp.513-525.

Humphrey, J.D., Strumpf, R.K., and Yin, F.C.P., (1989), "A Theoretically-Based Experimental Approach for Identifying Vascular Constitutive Relations", Biorheology, Vol. 26, pp. 687-702.

Kim, S.Y., Miller, I.F., Sigel, B., Consigny, P.M., and Justin J., (1989), "Ultrasound Evaluation of Erythrocyte Aggregation Dynamics", Biorheology, Vol. 26, pp. 723-736.

Kuo, C.-D., Bai, J.-J., and Chien, S., (1994), "A Fractal Model for Erythrocyte Sedimentation", Biorheology, Vol. 31, pp. 77-89.

Matsuo, T., Okeda, R., and Higashino, F., (1989), "Hydrodynamics of Arterial Branching - the Effect of Arterial Branching on Distal Blood Supply", Biorheology, Vol. 26, pp. 799-811.

Moser, R., Fehr, J., Olgiati L., and Bruijnzeel, P.L.B., (1992), "Migration of Primed Eosinophils Across Cytokine-Activated Endothelial Cell Monolayers", Blood, Vol. 79, pp. 2937-2943.

Oka, S., (1983), "A Note on a Theoretical Study of Erythrocyte Sedimentation", Biorheology, Vol. 20, pp. 579-581.

Oka, S., (1985), "A Physical Theory of Erythrocyte Sedimentation", Biorheology, Vol. 22, pp. 315-321.

Perktold, K., Peter, R., and Resch, M., (1989), "Pulsatile Non-Newtonian Blood Flow Simulation Through a Bifurcation with an Aneurysm", Biorheology, Vol. 26, pp. 1011-1030.

Pinchak, A.C. and Ostrich, S., (1976), "Blood Flow in Branching Vessels", J. Appl. Physiol., Vol. 41, pp. 646-658.

Plumb, O.A. and Whitaker, S., (1990a), "Diffusion, Adsorption and Dispersion in Porous Media: Small-Scale Averaging and Local Volume Averaging", in Dynamics of Fluids in Hierarchical Porous Media (ed. by J.H. Cushman ), Academic Press, New York, pp. 97-148.

Plumb, O.A. and Whitaker, S., (1990b), "Diffusion, Adsorption and Dispersion in Heterogeneous Porous Media: The Method of Large-Scale Averaging ", in Dynamics of Fluids in Hierarchical Porous Media (ed. by J.H. Cushman ), Academic Press, New York, pp. 149-176.

Sagayamary, R.V. and Devanathan, R., (1989),"Steady Flow of Couple Stress Fluid Through Tubes of Slowly Varying Cross-Sections - Application to Blood Flows", Biorheology, Vol. 26, pp. 753- 769.

Sato, M., and Ohshima, N., (1994), "Flow-Induced Changes in Shape and Cytoskeletal Structure of Vascular Endothelial Cells", Biorheology, Vol. 31, No. 2, pp. 143-153.

Schmid-Schonbein, G,W., (1987), "Rheology of Leukocytes", in Handbook of Bioengineering, edit. R. Skalak and S. Chien ), McGraw-Hill, N.-Y..

Shehada, R.E.N., Cobbold, R.S.C., and Mo, L.Y.-L., (1994), "Aggregation Effects in Whole Blood: Influence of Time and Shear Rate Measured Using Ultrasound", Boirheology, Vol. 31, pp. 115-135.

Takano, M., Goldsmith, H.L., and Mason, S.G., (1968), "The Flow of Suspensions Through Tubes. VIII. Radial Migration of Particles in Pulsatile Flow", J. Coll. Int. Sci., Vol. 27, No. 2, pp. 253-267.

Travkin, V.S. and Catton, I., (1992a), "Models of Turbulent Thermal Diffusivity and Transfer Coefficients for a Regular Packed Bed of Spheres", Procs., 28th National Heat Transfer Conf., ASME, HTD-Vol. 193, pp.15-23, San Diego, CA, August 1992.

Travkin, V.S. and Catton, I., (1992b), "Simulation of Suppresion and Transport of Power Generation Plant Effluents Based on a Unified Theory of Multi-Phase Modelling", Procs., International Conference ECO WORLD'92, pp.284, Washington, D.C., June 1992.

Travkin, V.S. and Catton, I., (1993b), "A Two-Temperature Model for Turbulent Flow and Heat Transfer in a Porous Layer", accepted to the "Journal of Fluids Engineering".

Travkin, V.S. and Catton, I., (1992c), "The Numerics of Turbulent Processes in High Porosity Nonuniform Porous Media", Procs. of the SIAM 40th Anniversary Meeting, pp.A36, Los Angeles, CA, July 1992.

Travkin, V.S., Catton, I. and Gratton, L. (1993c), "Single phase turbulent transport in prescibed non-isotropic and stochastic porous media," Proceedings of the 29th National Heat Transfer Conference, ASME, HTD-240, pp. 43-48.

Thurston, G.B., (1994), "Non-Newtonian Viscosity of Human Blood: Flow-Induced Changes in Microstructure", Biorheology, Vol. 31, No. 2, pp. 179-192.

Thurston, G.B., (1972), "Viscoelasticity of Human Blood", Biophysical J., Vol. 12, pp. 1205-1217.

Wheatley, D.N. and Malone, P.C., (1993), "Heat Conductance, Diffusion Theory and Intracellular Metabolic Regulation", Biology of the Cell, Vol. 79, pp. 1-5.

Whitaker, S. (1967), "Diffusion and Dispersion in Porous Media," AIChE Journal, Vol.13, No. 3, pp. 420-427.

Whitaker, S. (1977), "Simultaneous Heat, Mass and Momentum Transfer in Porous Media: a Theory of Drying," Advances in Heat Transfer, Vol. 13, pp. 119‑203.

Whitaker, S. (1986a), "Flow in Porous Media I: A Theoretical Derivation of Darcy's Law, "Transport in Porous Media, Vol. 1, No. 1, pp. 3-25.

Whitaker, S. (1986b), "Flow in Porous Media II: The Governing Equations for Immiscible, Two-Phase Flow," Transport in Porous Media, Vol. 1, No. 2, pp. 105‑125.

Womersley, J.R., (1955), "Oscillatory Motion of Viscous Liquid in a Thin-Walled Elastic Tube. I: The Linear Approximation for Long Waves", Phil. Mag., Vol. 46, No. 7, pp. 199-221.

Worthen, G.S., Smedly, L.A., Tonnesen, M.G., Ellis, D., Voelkel, N.F., Reeves, J.T., and Henson, P.M., (1987), "Effects of Shear Stress on Adhesive Interaction Between Neutrophils and Cultured Endothelial Cells", J. Appl. Physiol., Vol. 63, pp. 2031-2041.

Young, D.F., (1979), "Fluid Mechanics of Arterial Stenosis", J. Biomech. Eng. Trans. ASME, Vol. 101, pp. 157-175.