Burridge and Keller's Governing Equations of Linear Acousto-Elasticity in Porous Medium

Initial governing equations as they stated in many books (and given in the paper by Burridge and Keller (1981)) are

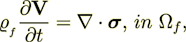	(1)
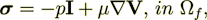	(2)
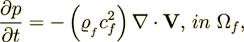	(3)
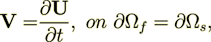	(4)
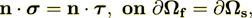	(5)
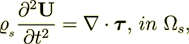	(6)
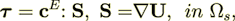	(7)

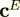where is the elastic stiffness (at constant electric field); 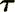is the elastic stress tensor; 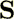is the elastic strain tensor; 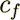is the sound speed in fluid; 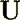is the displacement vector; 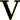is the velocity in fluid. This set of equations under applied time harmonic wave field

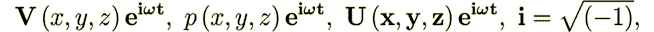	(8)

becomes in Burridge and Keller (1981) as eq. (3a)-(3g)

	(9)
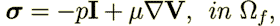	(10)
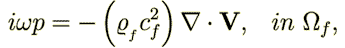	(11)
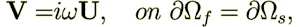	(12)
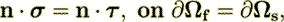	(13)
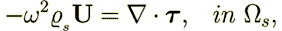	(14)
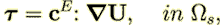	(15)

and after homogenization transformation when operator is changed according to 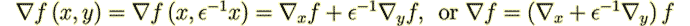, where

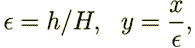
small scale domain size 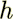by macroscale 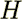, and where 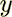is the "fast" short wave length independent variable, but 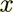is the long period "slow" argument, Burridge and Keller got (6a)-(6g)

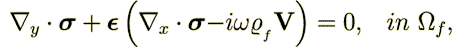	(16)
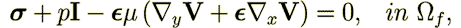	(17)
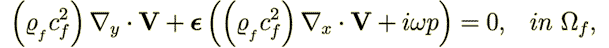	(18)
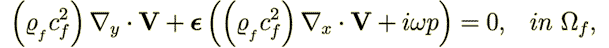	(19)
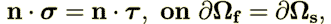	(20)
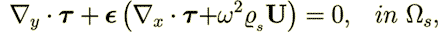	(21)
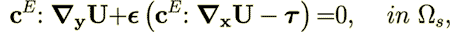	(22)

all in that using the replacement 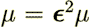,which is explained (p. 1141) due to scaling assessment (which is still the "assessment" thing to do).

Going further is - following the usual homogenization procedure to present a solution via the asymptotic power series

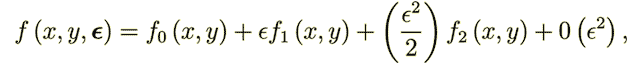	(23)

then solutions for the first two members are looked for in a form of a separate sets of equations (Burridge and Keller, 1981). For example, the first set, when and functions are 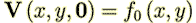, etc,. is (8a) - (8g)

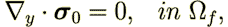	(24)
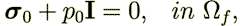	(25)
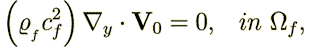	(26)
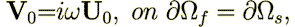	(27)
	(28)
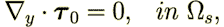	(29)
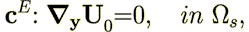	(30)

The Difference in Theories and Critique of Homogenization Theory

Comparison with VAT equations of momentum transport, for example, gives the understanding of the very substantial difference in governing equations.

Then now we will start to address the most dramatic portion of the homogenization development in Burridge and Keller (1981), which makes not only visually different equations appearance, but also means fundamental difference in the whole mathematical description.

Let start with the equations (20) -(21) on the page 1142 by Burridge and Keller (1981).

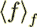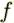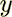Those equations have been averaged over the REV's fluid volume and get the right hand sides which are the averages of operators (we show the fluid averages variables as via the VAT notations as, for example, means the phase (fluid) volume averaged value of ) "with respect to over that part of "fluid phase" which is contained in 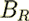"(spherical volume 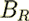is equivalent to REV )

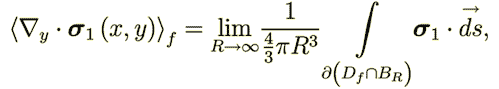	(31)
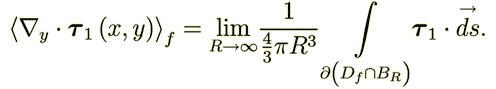	(32)

These two expressions obtained in such a way due to the specifics of applied homogeneous Gauss-Ostrogradsky theorem. Which is of the great difference with the VAT as we'll see now.

Those two integrals should be written and consequently calculated in the equations (because of the infinite limit .used in the definition) using the heterogeneous WSAM theorem as

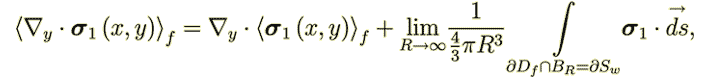	(33)
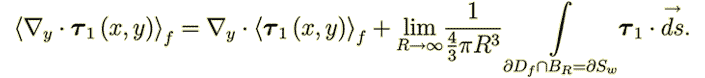	(34)

The problem is that in further treatment of equations (20) - (25) the following statements are written in the paper p. 1142:

"The surface 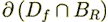consists of two parts, 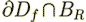and 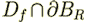.The former is that part of the pore surface within 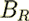while the latter is that part of the surface of the sphere 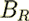within 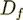." ..... "Thus the surfaces of integration in (20) and (21) can be replaced by the pore surface 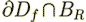without affecting the validity of these equations. Similar remarks apply when 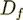is replaced by ."

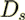And these latter 2 sentences mean the great difference to VAT theorems and the source of all further inappropriate equations they have done in this development. Because if this is not correct statement, then instead of

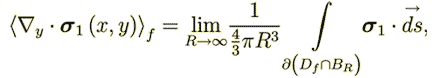one would have
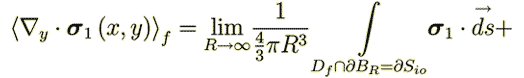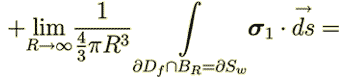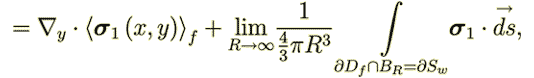	(35)

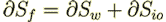where is the whole surface bounding the fluid volume where 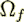, and 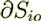is the surface of input and output of 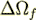in the REV.

When the formula (38) on p.1143

	(38)

used as the one which is supposed to be proven for other functions, it is incorrect, because the averaged term actually equals to the phase averaged value 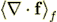in the VAT

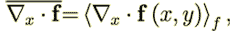	(36)

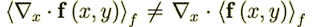and , but according to one of the averaging WSAM theorem it is equal to

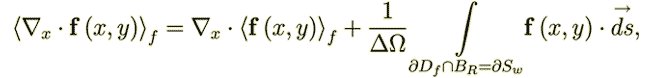	(37)

and through that theorem and others like that one would have a great number of interface and interphase phenomena being taken into account. Also, the averaging of non-linear terms was provided, (at least in the paper by Burridge and Keller (1981)) as they are linear terms.

We would like to summarize this short note regarding one of the best known non-HSP-VAT approach to acoustics in porous media as the two scale phenomena with these two remarks:

1) The homogenization approach (Homogenization Theory -HT) is the useful theory for those situations for which it was invented - as for the two scale inhomogeneous media with fluctuations. Nevertheless, the method and like "averaged" equations do not display the "Upper" scale correct equations, in the method used the second scale some properties to solve the lower scale problem.

Meanwhile, most of Heterogeneous media are more complicated and having the phenomena within the interface surfaces, and through the interface, though when phases have the discontinuities or sharp transitions at th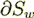e ,then the HT is not enough. It can not treat the sharp phase change, interface discontinuities, etc. for the Upper scale.

2) Because of those facts given above, to the important next question should be given more thorough investigation. What is the significance and value of difference in the problems with openly admitted interface boundaries movements and those with application of time harmonic presentation ?

As we have already studied, the time harmonic presentation can dramatically change the additional terms in HSP-VAT upper scale governing equations - those terms which control and determine the movements of interface during the wave propagation process.

We would stop short here to further investigate numerous non-HSP-VAT mathematical studies as well as HSP-VAT heterogeneous acoustics techniques. Few issues formulated for the wave propagation scaled statements in Heterogeneous Media we address in the "Electrodynamics" section at this web site. The formulations and treatments for linear acoustics and constant properties electrodynamics often are pretty close as many know.

For those, who found that their acoustics application belongs in the heterogeneous class of problems, we invite to Contact us