
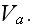

 For
instanse, a closed bubble in a plastic foam is considered locked within the
frame, and its volume therefore belongs to
For
instanse, a closed bubble in a plastic foam is considered locked within the
frame, and its volume therefore belongs to

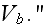
We would select from the number of relevant to the Heterogeneous Acoustics (HtA) studies the few as for arguments and discussion - Why it is so stubborn and in orthodoxy the most of education and research communities ?
Among studies pretending on new treatment of heterogeneous and even Hierarchical tasks in acoustics many still have a regrettable intention for citing the monograph by J.-F.Allard. That single action expose the misunderstanding of the field, at least, and we would like to put some analysis below in plane words without the hard intense mathematics, at least now for this field.
Some references continue to point out to the monograph by Allard, J.-F., Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, edited by Elsevier Applied Science, Elsevier Science, London, (1993); as the source of an expertise in Porous medium acoustics. We would say again (in addition) to what was said in the "Introduction" - Why this book is of no good content in this area.
Starting with the basic definitions, for example, regarding the volumetric averaging we can read in the book the strange statement as -
p.23: "Only the volume of air which is not locked within the frame must be
considered in

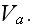

 For
instanse, a closed bubble in a plastic foam is considered locked within the
frame, and its volume therefore belongs to
For
instanse, a closed bubble in a plastic foam is considered locked within the
frame, and its volume therefore belongs to

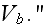
Why is that so? Well, everyone can see this statement as the same attempt to substitute the heterogeneous medium with the Homogeneous one, we wrote on these 50 like years "theories" in -
The equation of fluid (air) flow in a cylindrical pipe (pore) is taken in the
form (time-harmonic presentation), p.50:


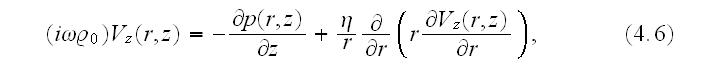
That is the starting point for the Lower level (scale) phenomena modeling. What is made with this modeling results for the Upper scale solutions and data reduction shown in the book using the same Lower scale definitions and equations.
And this is the discrepancy workers accustomed to neglect, because there is no proper understanding what should be the Upper scale (averaged) equations and their characteristics, data reduction methods and procedures.
It is interesting to take the excerpts and from the
p.69: "4.7 IMPEDANCE OF A LAYER WITH IDENTICAL PORES PERPENDICULAR TO THE SURFACE
....Two points

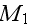 and
and

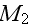 are selected at the surface of the material,
are selected at the surface of the material,

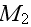 in free air and
in free air and

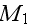 in the porous material. Let
in the porous material. Let

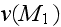 be the mean velocity of the air in a pore close to the surface and
be the mean velocity of the air in a pore close to the surface and

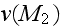 the velocity in free air in the plane field, the thickness
the velocity in free air in the plane field, the thickness

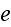 being neglected. The pressures
being neglected. The pressures

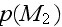 and
and

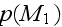 are the pressures in free air and in a pore, respectively. The continuity of
air flow and pressure at the surface of the porous material implies the
following two equations:
are the pressures in free air and in a pore, respectively. The continuity of
air flow and pressure at the surface of the porous material implies the
following two equations:
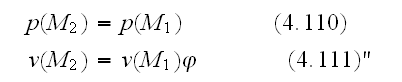
Well, these Boundary Conditions between two phases one of those is a porous are incorrect according to the scaled acoustic mechanics.
In the p.70 one can find :
"......The wave equation in a pore is
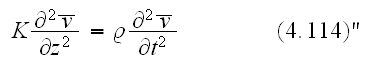
This equation is written in the monograph as like for the averaged velocity in a pore medium.
In the meantime, this is not the proper averaged Upper scale governing equation for a wave velocity. It can be written as in this form to seek for the effective density and bulk modulus, nevertheless. This is understandable, unfortunately, the point is that if the correct form upper scale equation is not known or wrongly presented, then we can not correctly determine - What and how to find out and what mathematics should be behind the estimations for the effective coefficients?
What is given on pages - pp.50-51 - equations (4.5)-(4.16) etc.; p.63 - equation (4.80) among others; p.64 - equation (4.88), for example, are the exact solutions for the singled out problems of transient (circular, wave induced) bulk velocity, and pressure determination in a separate tube (pipe, or pore, slit).
These solutions do not have relation to the declared "averaged" acoustic
wave equation in a porous media given as such in (4.114), because the averaged
acoustic wave propagation equations even for this morphology SPPM (Straight
Parallel Pores Morphology) and even with the rigid frame assumption have the
very different forms and that means the effective density

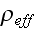 and bulk modulus
and bulk modulus

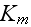 also do have different formulations.
also do have different formulations.
That means the p. 63, for example, statement "Equations (4.14), (4.48) and
(4.78) can be used to calculate

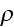 and
and

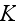 at a given angular frequency..." is not valid for the task of calculation of
the effective density
at a given angular frequency..." is not valid for the task of calculation of
the effective density

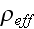 and bulk modulus
and bulk modulus

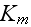 in the SPPM porous medium.
in the SPPM porous medium.
That means also that the physical and mathematical communication between the two scales the Lower and Upper models and governing equations can not be constructed based only on the known solutions (even exact for some problems) of the Lower only level of modeling.
In chapter 5 given an approach to the sound propagation modeling in porous media with the rigid frame using the incorrect methodic suggested in works by Johnson et al. (1987) with the definitions of dynamic permeability and tortuosity. We used to comment on these invalid averaging techniques in -
p.79: "In the case of common porous materials, a modeling of the bulk modulus and the effective mass of the air, from the geometry of the frame, is generally impossible. This explains why the models that describe sound propagation in these materials are mostly phenomenological.... "
That's not true - in HtA (HSP-VAT) the two-scale statements are available definitely and the solutions, modeling, and simulation are open to pioneers and for the industry introduction.
also in this page one can read about the definition of the averaging in porous media:
pp.79-80: "Let us denote by

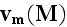 the microscopic velocity at M. The macroscopic velocity
the microscopic velocity at M. The macroscopic velocity

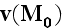 around
around

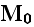 is obtained by averaging
is obtained by averaging

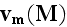 over a small volume
over a small volume

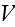 around
around

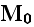 including several pores
including several pores
![]()
the symbol

![]() denoting the averaging over
denoting the averaging over

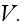 "
"
This definition is unclear at least.
Also in p. 80 there is the incapacitate definition of the variations in the
ratio of nonlinear (squared) averaged function (velocity in this case) in
formulae
(5.3;
 5.4).
5.4).
In chapter 6 given an approach based on the Biot's description of the sound propagation modeling in porous media that having an elastic solid phase (frame).
p. 118: "As shown previously, precise predictions for sound propagation in ordinary rigid framed porous materials are generally difficult to obtain, due to the complexity of the frame geometries. For the case of materials having an elastic frame, the description of sound propagation is more complicated.
A general model exists, the homogenization theory [1-7], that links the macroscopic and the microscopic descriptions of sound propagation. ....."
We have shown in our piece of analysis on the web in -
that this is still the one scale mathematical and physical description and that the many, if not all the Upper scale characteristics of propagation features are not possible to get with the Homogenization theory modeling.
p. 128: equations of sound wave propagation in fluid (air) and solid phase (6.52; 6.53 ), for example, are the usual complicated Homogeneous equations with the introduced few additional coefficients the whole role of those is to provide for the communication between the physics of the Lower scale phenomena that is obviously working and for the Upper scale, but existing Homogeneous language of mathematical and physical description was incapable to write that effects out correctly and in explainable form.
The Biot's theory is used as the theory that should be followed. Meanwhile, this is the theory that was developed and grounded in 50th as the highest level of generalization for heterogeneous acoustics. It was one of the many similar Homogeneous physics concepts sought and flourished for "Heterogeneous" and scaled fields in physics in 40th - 80th of the last century, again see more comments in -
1) All the data and results obtained in a way that might be named the
"reverse acoustical engineering" of known circular solutions for 1D wave
equations as (4.114), for example, and known data, and definitions for the
impedance

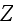 ,
effective density
,
effective density

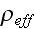 and bulk modulus
and bulk modulus

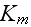 of some porous (heterogeneous) materials.
of some porous (heterogeneous) materials.
2) In the way of doing this reverse engineering of the Upper scale
characteristics as impedance

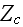 ,
effective bulk medium wave number
,
effective bulk medium wave number

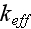 ,
effective density
,
effective density

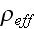 and bulk modulus
and bulk modulus

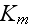 the averaged functions (one pore, pipe) are used for the similar to one
element homogeneous mathematical problems.
the averaged functions (one pore, pipe) are used for the similar to one
element homogeneous mathematical problems.
3) This is the same (or close to) situation with the problems of the same kind two-scale statements in Fluid Mechanics, Thermal Science, Electrodynamics, etc., when the one single element solution of medium at Lower scale are brought to the closeness to the some known characteristics of the Upper scale by pure analogy. Few of the most known problems are detailed in the area that is profoundly used in transport modeling - the Multilayer diffusion, conductance through the two-phase alternative media -
4) While browsing through the two-scale solution one can notice, that the constant phase coefficient problem solutions at the Lower scale can predict some characteristics of the Upper scale, but not all of them. Also not knowing why this or that happening (meaning no design possibilities), and these solutions do not exist for even slightly more general statements, for example, when the second pore size - even one element of the second size, or any morphology detail are introduced. For that - no solution or method exists, but HSP-VAT only.
In Fluid Mechanics this is the flow in porous medium model of one diameter pore - might be the best example for comparison.
For the two diameters pores (tubes, pipes) flow the Upper scale bulk, averaged solutions and characteristics do not exist in the category of Homogeneous physics, see our -
and
5) Meanwhile, the Upper Scale (averaged) equations in a separately taken
fluid phase or in a bulk two-phase medium are completely of different form than (4.114).
Thus, the mathematical formulation for the Upper scale (only looked for) HtA
equations and their averaged characteristics suggested to seek interpretation
for averaged wave number

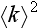 and effective wave numbers
and effective wave numbers

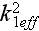 ,
,

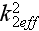 ,
,

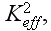 rather than experimenting with the non-existing in averaged equations
effective "density"
rather than experimenting with the non-existing in averaged equations
effective "density"

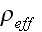 and
effective "bulk modulus"
and
effective "bulk modulus"

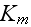 numbers.
numbers.
6) By the way, even if the assumption of rigid frame was adopted in the
averaged Upper scale HtA equations, one can find out that the interface
surface velocity of vibration
(
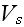 )
is in need for a proper evaluation of acoustic fields.
)
is in need for a proper evaluation of acoustic fields.
1) You can not find (calculate) the sought after Upper Scale bulk
characteristics such as - neither the reflection and absorption coefficients
nor the effective density

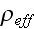 and bulk modulus
and bulk modulus

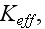 etc.
etc.
2) You can not solve the phase specific and phase averaged acoustic problem correctly.
3) You can not solve this one of the simplest problems - the SPP morphology (SPPM) for the Upper (averaged fields) scale even when it is the one pore diameter medium - solutions by Biot, Allard, etc. are for the Lower scale characteristics only. If only one diameter of pores (channels) is different from others or varying one from another and along the single coordinate of axis of pores then the problem is untreatable in Homogeneous acoustics.
Not for the fluid (air) phase wave propagation nor, of course, for the two-phase problem stated.
4) You can not solve a one HtA problem where (when) the physics on the boundary surfaces is taken as for the homogeneous media - because there are the different BC should be applied for heterogeneous problems. At the meantime, the homogeneous acoustics does not know - How to define and introduce those BC.
For example, when a silencer (liner) design is being considered - the only tools they continue to rely upon is the experimental work-studies with the data reduction models as for a "Luna orbiter."
There is no one more or less realistic heterogeneous conceptual, modeling, technical approach, but used the one scale homogeneous models.
Watson, W. R., Nark, D. M., and Jones, M. G., "Assessment of 3D Codes for Predicting Liner Attenuation in Flow Ducts," 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), Session 5- AA-5: Duct Acoustics I: Engine Modeling and Duct Propagation, 2008.
Syed, A. A., Yu, J., Kwan, H. W., and Chien, E., "The Steady Flow Resistance of Perforated Sheet Materials in High Speed Grazing Flows," Report STI, NASA/CR-2002-211749, GE Aircraft Engines, pp. 1-103, 2002.
Perrot, C., Chevillotte, F., and Panneton, R., "Bottom-up approach for microstructure optimization of sound absorbing materials," JASA, Vol. 124, Iss. 2, pp. 940-948, 2008.

![]()