 And why they need to use these concepts and tools?
And why they need to use these concepts and tools?
The Annals of Frontier and Exploratory Science
Saga of Dr. Kushch, V.I., 1994-2009
Now Gatekeepers and Wheel Re-Inventors:
UCLA MAE Department Professors
What is the False Continuum Mechanics of Heterogeneous Media - Continuation of Reviews on Heterogeneous, Multiscale Treatment:
Any information displayed here is the proprietary information in the area of Continuum Mechanics analysis of the current state of affairs.
As long as people in the field continue to use the public money support and do the incorrect, wrong science for that money, we can freely devote subtitles as "gatekeepers" and "wheel re-inventors" to them.
These authors in spite of the fact that their work is about the scaled heterogeneous media are not seeking and not using the only correct, appropriate, created for these purposes tools because:
1) They don't know that other than Gauss-Ostrogradsky theorem exists for Heterogeneous media - the WSAM theorem. Meanwhile, few of them do know. 2) They don't know, don't develop and don't want to know whether - the Governing Equations (GE) of the Upper (in most situations) scale physical fields exist?3) They don't know and don't want to know - What are these HSP-VAT GEs?
4) What are the Upper scale GE
 And why they need to use these concepts and tools?
And why they need to use these concepts and tools?
5) They don't solve the equations of the 2-nd (Upper) scale. The equations they sometimes present as of the Upper averaged space are incorrect.
No, this is the deed of great number of just errors, wrongdoings. People doing theoretical, mathematical, and experimental (because their experiments are controlled by their theories - we spoke on that many times) errors in their research, they use public money and they deliver the trash or misrepresentations as in Dr. Kushch's work, see below.

Dr. V.I.Kushch is an outstanding veteran Gatekeeper and Wheel Re-Inventor.
Has been since 1994.
Dr. V.Kushch for more than 20 years doing solutions of actually one problem - Low scale local composite media exact analytical elucidation while the effective field for one of the phases - matrix, being assigned. He became a great internationally known specialist on this problem. The problems are stated in such a mode, that the method should be called - Effective Field Method with the One Phase Assigned Nonlocal (Upper) Scale Solution and Assigned the Macrostrain (or other field) Values. Also with the Macroscopic strain value assigned as 1. We show below why this arrangement is helping to go Upstairs to the Second nonlocal Upper scale effective coefficients. Anyway incorrectly assessing them - we discuss that below why.
He started to study and work for me in 1994 as a contractor. He was taught on numerous issues of HSP-VAT as of general concepts and ideas, general theorems and math and applications primarily for Thermal Physics and Fluid Mechanics.
Dr. Kushch signed the Nondisclosure Agreement in 1994 for 10 years. I had assigned to him and disclosed some information that was not available at that time, some of that information, techniques are not available up to now.
We spent a huge number of hours on my visits to Ukraine, Kiev in 1994-1997, and more hours, days, and months for email exchange, stating the problems and discussing the outputs.
He was not too happy with work and assignments, as well as I was not happy with his 3 year long attempts to dethrone, refute the HSP-VAT math and physics.
In doing this he had done with me the very good studies and simulations for problems that were in his second doctorate's agenda in his institution. He had not performed finally the simulations that I had assigned to him for start - the simulation of the two-scale local-nonlocal and second scale nonlocal equations for a few morphologies and calculation of the effective coefficients for the Upper scale HSP-VAT governing equations.
Nevertheless, in 1997 despite signing the NA for ten years he published two papers (of which only I know) - Kushch (1997a, 1997b) where some definitions of HSP-VAT had been used.
And were used incorrectly - the effective coefficients were calculated wrongly - I have done analysis of the papers only in 2001-2002 and some of the texts related to (1997a) was published in -
So, the errors went unanswered and are staying up to now as the incorrect data for comparisons, as the "litmus data"? for other scientists in the CM field.
The second paper review in terms of the alleged macroscopic, averaged characteristics for elasticity in heterogeneous medium is given here in this script.
Finally, in this way Dr. V.Kushch became a conscious gatekeeper for HSP-VAT because in a three year period being allowed to recognize the internal features and mathematical details in implementation of HSP-VAT for Thermal Physics and Fluid Mechanics he was not able to find out any fundamental wrongdoings, errors in HSP-VAT. He did not refute this science.
More on that - Dr. Kushch himself took part in the development of simulation procedures for the HSP-VAT.
Well, after all he chose to be sided with his "homogeneous" book (Golovchan et al., 1993) elasticity mechanics statements and his, might be, personal ego while doing the false science in elasticity mechanics of heterogeneous media and composites since 1994.
That was his choice.
Our choice is to put at last this story before public eyes for educational and pedagogical purposes - as it is said - people are controlled by their agreements and by ethics of them.
Since then, for more than 14 years Dr. V.Kushch has been doomed to be also the Wheel Re-Inventor. Because for more than 40 years the better, more precise, and fundamental tool for Heterogeneous, Scaled and Hierarchical physics than the HSP-VAT has not been invented!
But Dr. Kushch continuing to publish a very good Lower (ground) scale solutions for heterogeneous two-scale problems in Elasticity theory, CDM with the consecutive wrong deliberations for the Upper scale properties.
Involving his co-authors and funding agencies in this conspiracy as well.
To our knowledge, Dr. V.Kushch never publicly delivered decisive "disproove" of HSP-VAT as was doing, for example, for near 10 years Chinese physicist regarding the Boltzmann equation. Even in the online manuscripts as C.Y.Chen does -
Now, it appears that all co-authors of Kushch in the US and other countries should be aware at least of what kind of mistakes they have been doing when consider the composite's elasticity, plasticity and CDM problems as of a prime ground scale - the Lower conventional homogeneous physics problems and later on doing the generalization of simulation calculating the "Upper" (second) scale nonlocal "effective" coefficients and like "estimations."
All those are suffering from mistakes of using inappropriate averaging techniques with the GO theorem.
And these mathematical constructions are incorrect.
To the misfortune of the Conventional one-scale for all (OSFA) Heterogeneous Continuum Mechanics (HtCM) the workers like Dr. V.I.Kushch are of plenty. We will still be taking to the Histology table the most interesting works and disclose to students and sober young researchers the path of mistakes in current HtCM.
Recently, doing my studies I again accidentally came across of writings by Kushch and his co-authors on solid state mechanics, elasticity theory, continuum damage mechanics in heterogeneous, multiphase materials, composites.
That can be counted as of ~ 14-15 years of incorrect studies and influences on the US funded workers.
Well, those researchers themselves make up the problems in that kind of homogeneous pretending to be "heterogeneous" studies. But that is another story.

Introducing the Heterogeneous Continuum Mechanics Actively Publishing Now Gatekeepers and Wheel Re-Inventors - Kushch, V.I., Sangani, A., Buryachenko, V.A., Sevostianov, I., Mishnaevsky, L.Jr., and their co-workers, etc., in addition to professionals mentioned in our -
Excerpts from (Kushch et. al (2009)):
In page 1574 in the abstract one can find that:
"This paper addresses the problem of calculating effective elastic properties of a solid containing multiple cracks with prescribed orientation statistics. To do so, the representative unit cell approach has been used. The microgeometry of a cracked solid is modeled by a periodic structure with a unit cell containing multiple cracks; a sufficient number is taken to account for the microstructure statistics. "
" The exact finite form expression of the effective stiffness tensor has been obtained by analytical averaging the strain and stress fields. "
In page 1577 one can find that:
"By adding 2D model, we assume

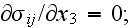 within this framework, the
within this framework, the
(a) anti-plain shear (in

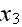 direction) and
direction) and
(b) plane strain problems are considered. In the first case,

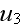 is the only nonzero component of the displacement vector
is the only nonzero component of the displacement vector
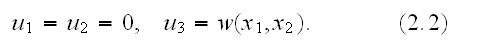
Also, we have two non-zero
components of the strain and stress tensors, they are

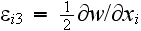 and
and

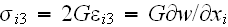 ,
i=1 and 2, respectively, where
,
i=1 and 2, respectively, where

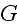 is the shear modulus of a solid. The stress equilibrium equation
is the shear modulus of a solid. The stress equilibrium equation

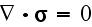 in this case reduces to the 2D Laplace
equation
in this case reduces to the 2D Laplace
equation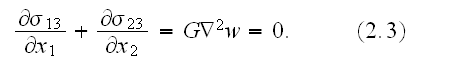
It enables finding

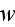 as
as

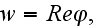 where
where

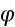 is an analytical function of the complex variable
is an analytical function of the complex variable

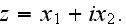
In the plane strain problem, we have



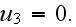 The complex value displacement
The complex value displacement

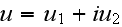 as well as its derivatives (strain and stress tensors) can be expressed in
terms of two complex potentials,
as well as its derivatives (strain and stress tensors) can be expressed in
terms of two complex potentials,

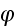 and
and

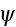 (Muskhelishvili, 1953). We write
(Muskhelishvili, 1953). We write

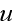 as
as
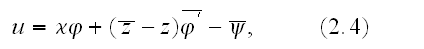
where

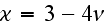 and
and

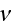 is the Poisson ratio of a crack-free solid. Components of the stress tensor
are given
by
is the Poisson ratio of a crack-free solid. Components of the stress tensor
are given
by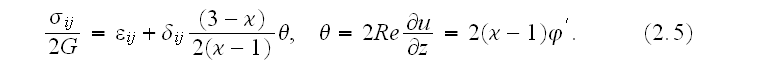
We assume the strain and stress fields to be macroscopically uniform and
defined by the constant macroscopic strain tensor components

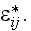 Due to the cell-type periodicity of geometry, the displacement field is the
quazi-periodic function of coordinates:
Due to the cell-type periodicity of geometry, the displacement field is the
quazi-periodic function of coordinates:
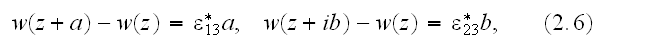
and
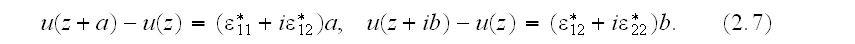
In the model, we consider the crack surfaces

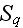 defined by
defined by

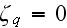

 are traction free, i.e., we assume the cracks to be open. "
are traction free, i.e., we assume the cracks to be open. "
Our comments:
here in the BC (2.6) and (2.7)
the local variables are connected to the macroscopic variables directly as all
of them are the local ones. This is the frivolous
scaleblending - the term we are using to call the
unjustified action or procedure (often even mathematical) that equals or makes
simple linear (most often) or other appropriate at the moment mathematical or
verbal dependency between the local (lower scale) and of the Upper (nonlocal,
scaled) physical fields.
In page 1578 one can find that:
"We assume the stress field in
a solid with cracks is induced by the far field constant strain tensor

 "
"
Our comments:
And Dr. Kushch knows about this.
because later on this globally assigned
tensor components will be concerned and used in the problem's second scale
simulation assessments - it will be used for the macroscale strain computed based
on the microscale local solution, that is the incorrect
implication of the Upper scale field for the incorrectly simulated
Lower scale fields.
In page 1579 one can find that:
"3.3 Effective stiffness tensor
The above analytical solutions provide an accurate evaluation of the local
fields at any point of the unit cell as well as the stress intensity factors
(SIFs) at the crack tips. Their detailed analyses is a subject of a separate
paper: for our purpose, it is important that these fields can be integrated
analytically to obtain the exact, closed form expressions for the effective
elastic moduli of a cracked solid, defined by the
formula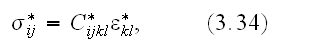
where

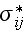 are the volume-averaged, or macroscopic stresses:
are the volume-averaged, or macroscopic stresses:

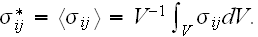 In our case,
In our case,

 .
And, since the components of the mean strain tensor were taken by us as the
input (load governing) parameters, all we need to determine the effective
stiffness tensor is to integrate the local stress field. Indeed,
.
And, since the components of the mean strain tensor were taken by us as the
input (load governing) parameters, all we need to determine the effective
stiffness tensor is to integrate the local stress field. Indeed,

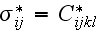 ,
where the stress field corresponds to the uniaxial strain
,
where the stress field corresponds to the uniaxial strain

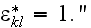
Our comments:
and which is the wrong formula, because the effective
characteristics on the Upper scale are determined via the different equations
and averaging mathematics.


In page 1580 one can find continuation of the thought:
"Averaging the anti-plane shear stress gives us
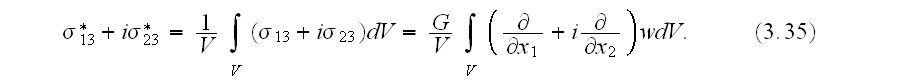
The Gauss formula yields
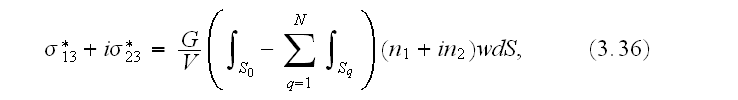
where

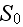 is the outer boundary of the cell,
is the outer boundary of the cell,

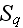 is the q-th crack surface and
is the q-th crack surface and

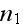 are the components of the outward normal unit vector.
are the components of the outward normal unit vector.
Accounting for the displacement field periodicity, we obtain
expectedly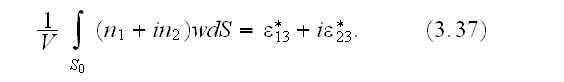
As to the integrals over the cracks' surfaces, they can be written as
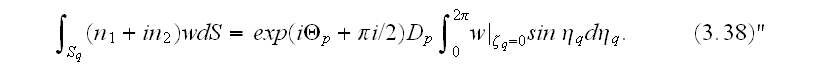
Our comments:
and which is the wrong formula as well.
In (3.37) the matrix averaged value assigned as of the two-phase?
In (3.38) cracks should be of the two kinds not one.
The WSAM theorems and consequences should be used.
Let's explain this with more graphical detail.
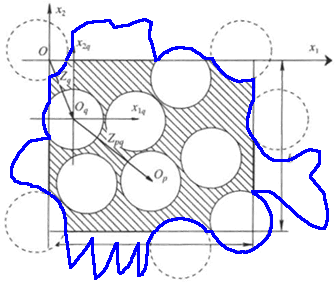
The features of the REV by present authors we should discuss in this review are shown in
Well, the trick here is that the REV is taken including all the cracks seen in the figure.
In this case the cracks always to be included within the REV and Kushch and co-authors can use assigned up-front the strain tensor with consequtive elimination of integration over the ANY boundary of matrix phase.
That means also that the matrix bounding surface can be freely drawn.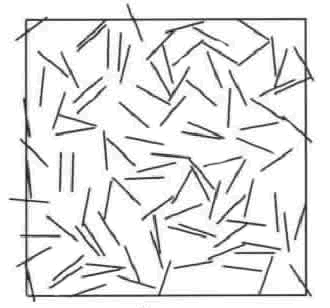
Our comments:
Meanwhile, the real correct REV drawn ought to be intersecting any phase that might occur in the way of drawing
We address this issue with more detail in the review of the following paper - Kushch et al. (2008a).
1) The lack of heterogeneous media scaled understanding brought out the
strange and erroneous statements used throughout the literature on Homogeneous
Continuum Mechanics applied for heterogeneous problems, that the assignment of
the remote initial values for like "bulk" strain

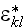 and stress
and stress

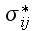 in the composite automatically determines the matrix effective, "bulk"
characteristics
in the composite automatically determines the matrix effective, "bulk"
characteristics

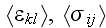 .
.
That is the trick, because those properties are not equal. These characteristics
are of different media and of different scales even.
Nevertheless, based on this erroneous assumption - the great number of studies
using the definition that the only functions they need to simulate are of the
inclusions phase, because the matrix phase effective properties are known as assigned?
Which is wrong for heterogeneous, scaled physics and math.
2) We can not write the equality (2.6)
because the mean macroscopic strain tensor
This is the two scale problem, and effective macroscopic coefficients of this
kind are not defined and equal to just differentiated or averaged
volumetrically (meaning in most cases also stochastically) microscopic
fields.
And Dr. V.Kushch knows about that, this is the most interesting.
3) We can not avoid mentioning an important feature of analytical solution -
it is to give a guide and the cornerstone assessment and results for future
controlled comparison.
So, it is vitally important to have correct analytical solutions. In problems with the Kushch's
solutions for the two-scale local-nonlocal heterogeneous problems we have not gained this
advancements, because the Upper scale results, estimates by Kushch and co-authors
(but works with V.S.Travkin over the HSP-VAT two-scale heat transfer, fluid mechanics, and
the two-scale simulation) are wrong.
4) Taking into account the incorrectness of the Upper scale estimates in
this paper (Kushch at el. (2009)), the pages starting from p. 1581 - are not
worth to read - the published data is incorrect.
5) In (3.38) (Kushch at el. (2009a)) should be written
6) In p. 1580 left pane - the
text has the hidden fact and mathematical errors that consist of the
mathematical treatment of the outer surface
This is so important hide that I was forced to write the whole piece of
analyses deliberating the truth why this intersection is so important to hide
for the conventional homogeneous, one-scale physics, including electrodynamics
and, of course, elasticity mechanics, presented in the "Heterogeneous
Electrodynamics" section of this website -
The disregard of detailing of REV definition and preservation of the concepts of Averaging Volume started by some prominent members of Continuum Mechanics community many years ago to hide the neglect of the newly born HSP-VAT
and were noticed in publications at that time. We wrote on this many years ago also and this opinion is in publications and in the web
particularly in the critics of work - Brenner, H. and Adler, P.M., "Dispersion Resulting From Flow Through Spatially Periodic Porous Media. II. Surface and Intraparticle Transport," Phil. Trans. R. Soc. Lond., Vol. A 307, pp. 149-200, (1982).
This disdain of the REV's features and more of that the declaration of unimportancy of the exact form and concept of drawing the REV was done, our guess, to disregard the HSP-VAT or Averaging Theory quite different conceptual approach to the Scaled, Nonlocal Continuum Mechanics Governing Equations (GE) at that time - ~30 years ago, that was still the new direction needed to be destroyed.
Destroyed, because the Non-invariant GEs for the same problem, for the same phenomena but at different scales have been appeared in the CM, and that was a heresy at that time?
7) That means also the formula (3.38) (in the Kushch at el. (2009a)) is
incorrect as well, as soon as it doesn't distinguish the internal cell's cracks
and the intersecting boundary cracks.
8) We need to stress this out that it can not be written based on a
"periodicity" the formula (3.37)
because no matter what, the "mean strain tensor"
This was explained hundreds times in literature on thermal physics and fluid
mechanics.
Just because the simple volume averaging, and incorrect averaging (Dr.
V.Kushch has been taught in detail on averaging procedures in 94-97, and knows
on the problems with the "mean" and the "averaged," phase averaged and
intrinsic phase averaging functions) does not constitute the effective strain
tensor. The mean and the effective coefficients are often not the same
functions as they are and in this case.
That is - the (3.37) is invalid by definition, so
the macroscopic strain tensor
9) Regarding the "famous" often simply hidden, but crucial for Kushch's and other researcher's methodology - that the centers of inclusions should not lay down exactly at the boundary of the REV? We need to state that this restriction is not applicable or even reasonable requirement at all, it is quite artificial and can not be maintained as long as the REV can and should be moving over the space for averaging process to be performed.
The REV can be placed at any location and serve for any assessment locally within the problem's region.
10) It is worth to note here also, that this kind of problem for composites refined and described in the two-scale local-nonlocal HSP-VAT statements allow analysis and results to be obtained that are unachievable with the kind of 1-scale elasticity formulations as Dr. Kushch does with his co-authors.
See some of the outcomes of that kind in -
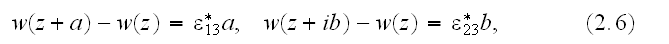

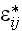 can not be defined by this method as via the differential of microscopic
displacements vector components.
can not be defined by this method as via the differential of microscopic
displacements vector components.

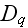 not
not

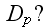

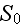 that is presented in the Fig. 1 as it is intersected by cracks, but the crack's surfaces
that is presented in the Fig. 1 as it is intersected by cracks, but the crack's surfaces

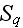 in real treatment are considered as if they are not intersected by the outer
in real treatment are considered as if they are not intersected by the outer

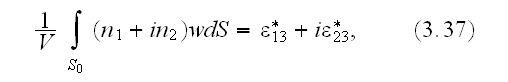

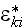 was taken as the assigned input (load governing) parameter, and that assigned
tensor
was taken as the assigned input (load governing) parameter, and that assigned
tensor

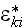 is not the mean strain tensor within the medium of the problems. Because the
mean effective strain tensor
is not the mean strain tensor within the medium of the problems. Because the
mean effective strain tensor

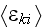 within the heterogeneous medium determines with the HSP-VAT mathematics and
procedures very differently of what is considered in homogeneous CM
presentation followed in this study.
within the heterogeneous medium determines with the HSP-VAT mathematics and
procedures very differently of what is considered in homogeneous CM
presentation followed in this study.
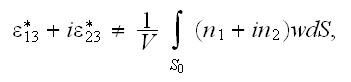

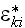 and the microscopic displacement components
and the microscopic displacement components

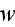 are connected in a very different way.
are connected in a very different way.
1) The lack of heterogeneous media scaled
understanding brought out the strange and erroneous statements used throughout
the literature on Homogeneous Continuum Mechanics applied for heterogeneous
problems, that the assignment of the remote initial values for like "bulk"
strain

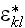 and stress
and stress

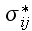 in the composite automatically determines the matrix effective, "bulk"
characteristics
in the composite automatically determines the matrix effective, "bulk"
characteristics

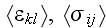
That is strange, because those properties are not equal. These characteristics
are of different media and often of different scales even.
Nevertheless, based on this
erroneous assumption - the great number of studies using the definition that
the only functions they need to simulate are of the inclusions phase, because
the matrix phase effective properties are known as assigned?
Which is wrong for heterogeneous, scaled physics and math.
2) The great, fundamental fault of all of this kind local-nonlocal,
pseudo-Upper scale effective characteristics - "effective" stiffness tensor,
"effective" strain
For example, while tackling the strain tensor Kushch and co-authors (2009; 2008a; etc.)
wrote the volumetric averages without any thought about the Hooke's law
separately from the elasticity governing equations or the Upper scale in the
respected two or more phases, dropping the part of boundary conditions -
tractions at the interfaces, external boundary of the REV (they used the
"invented" RVE notion), etc.
That kind of cheating or ignorance give the possibility to write the wrong
equality in Kushch et al. (2008a), for example,(as well the same kind of
statement in every their study)
where
By doing this assignment the half-problem has become known
(well, in reality for Upper (averaged, non-local)
scale we can not do such a simple assignment!)
and, at the same time - the problem of the
Boundary Conditions (BC) at the Upper macroscopic scale has been created.
That is because the local strain tensor at the boundary from outside can not be
easily assigned with using the homogeneous formulae for the BC for the nonlocal fields and
for the "averaged" strain.
And Dr. V.Kushch knows about that, which is the most interesting.
Because in 1994-97 we provided the specific studies on the BC between heterogeneous and
Homogeneous media to state the Upper scale BCs. Because the great prevailing
number of
problems are interesting and significant for practice when being stated as
the Top-Down
heterogeneous problems. As, by the way, might be the problem stated
in the Kushch et al. (2009).
Assignment of the Upper scale strain
is actually the "half-solution" of the problem, as soon as
(3.37) and in all other like (3.37) formulae in reviewed here studies by Kushch,
is satisfied because of this assignment!
In this way authors assign (found) the nonlocal Upper scale solution in the matrix just at
the beginning.
3) Also, the assignments of the Nonlocal macrostrain means not only assignment of the one
phase solution actually - see our comments above, to other papers by Kushch, and elsewhere
in this website section on Ht Elasticity, Continuum Mechanics, but also the almost
unsurpassed technical difficulties with the BC and this Upper (nonlocal) scale problem -
because the nonlocal boundary condition would demand the assignment also of the surficial
integrals near the boundary within the heterogeneous medium already.
Then, the assignment of both phases nonlocal HSP-VAT boundary conditions with surficial
values means in turn the solution of the both Upper Scale displacement - strain fields problem
in need.
Which means, in turn, the general solution of the Upper scale HSP-VAT statement,
that Dr. Kushch fiercily avoiding since 1994.
4) This is the danger of ignorant usage of the Upper scale (macroscopic)
variables to
instantaneously (and not innocent) presenting the Lower scale
(microscopic) wrong
averaging operations for "finding" the "effective" strain?
That is unacceptable.
5) In this way of doing "multiscale", "macroscopic" - in reality screwed
homogeneous one-scale media elasticity theory, continuum damage mechanics,
general continuum mechanics of heterogeneous, scaled media (HSM) - authors not
only do incorrect the Upper scale (macroscopic) assessments, simulation. And
often even the Lower scale simulation is going wrong, because they assume the
different scales variables can be taken as equal. This we call the
Scaleblending.
They have lost the substantial part of a real science for Heterogeneous Scaled
Media. This constitutes a great loss both for science and technologies and the
financial loss for wrong, unnecessary studies.
This also makes a wrong design of heterogeneous materials, devices as, for
example, in their Kushch et al. (2008b) composite CDM study authors in p. 2759
write that -
"The composites of primary interest for us are the unidirectional glass fiber
- epoxy matrix FRC's. The pre-requisite of using these materials in the wind
turbine components is extremely high
(~
How dare they do this if their Upper and Lower scale models were stated
without the Scaleportation presented in any slightest hint?
Well, and they don't have and will not have the proper clue on - How to do the Heterogeneous experiment which can confirm the Homogeneous theoretical results?
Because of many inconsistencies we are writing here about.
6) In this way of doing the two-scale problems as the one scale authors
are loosing the chance to address the most interesting phenomena in the
physics of
composite media - the phenomena at the interfaces.
This is not achievable with the one scale local homogeneous mechanics.
And Dr. Kushch has been knowing about this.
7) Dr. Kushch certainly uses the HSP-VAT techniques, but in a silent, hidden way, as we point
out here. The few most interesting phenomena occurring
at the interface in composites
with damages, cracks as in Kushch et al. (2009) become lost for investigation
with the wrong
use of a homogeneous approach. One more example is that, here in the problem described by Kushch
et al. (2009) should be derived the Macroscale nonlocal equation of elasticity equilibrium
for the one phase only - for the matrix phase. But it was not done?
Meanwhile, the
elements of the one phase treatment were presented in the study albeit with more errors than
Kushch usually demonstrates. My guess, that in this (2009) study his co-authors tried
to get a lead, and failed.
8) While avoiding modeling and simulation formulated in terms of HSP-VAT for
the Upper scale fields authors of this group, and others we will be
deliberating on, acting to prevent themselves from the Upper scale
problem's features:
8.1) They can not formulate, even to know, and investigate most of the Upper scale characteristics of interest: a) both scale surficial characteristics; b) both scale fluctuation characterisics, etc.
I am sure most of Dr. Kushch co-authors never knew about those? But he does.
It is interesting to note, that both surficial and fluctuation characteristics Dr. Kushch himself simulated and studied with me in 1995-96 and we derived at many interesting features on those parameters, some of them are unpublished yet.
8.2) They can not study morphology parameters of Ht Elasticity, Plasticity, Continuum Damage
Mechanics, etc. Morphology parameters formulated and sought after as of the Upper scale - not
those people usually count for, as - number of cracks, statistical characteristics of cracks,
length of the cracks, etc. All these are of the Lower scale parameters not of the Upper one.
8.3) They can not study the properties of the interface - correctly determining the
arisen characteristics, because the interface is that thing that connects and communicates
the both phases (if really both, the declaration of each inclusion a separate phase
mostly serves to the fogging the problem features) and has the own characteristics.
Those would be studied later when researchers learn how to formulate the issues.
It is not surprising that Dr. Kushch carefully writes about interface, and actually
does not study the interface effects in composites, even in the study on debonding - Kushch et al. (2008b)? Why is that?
9) It can be said that the analyzed above issues are related to the problem of Scaleportation from Lower scale local field solutions to the Upper scale averaged nonlocal, but mostly sought after fields. These fields include also the effective properties of composites, heterogeneous media. As we have depicted above the problem of scaleportation is itself not a trivial task of simulation with the Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) homogeneous physics mathematical statements.
10) Here, the remark is appropriate on that the option authors usually
include in the like by Dr. Kushch's statements, that the number of
phases N can be substantially >1, means actually that the problem
is stated with the phase dependent coefficients or C_{ijkl}(x).
Well,the Upper nonlocal GEs become much more cumbersome and tricky
for analysis and solution then in the case of two phases.
11) It is interesting to mention regarding the use of assigned averaged
strain and stress values - Whether authors thought about the verification
of their solution and simulate the values of effective strain and stress
by averaging the Lower scale local displacement fields?
And they would find out the nonconservative fields. Which is
inexplicable in Homogeneous CM.
12) Not the last and definitely not the least remark is that the
assignment of the averaged gradient of the strain field (other physical
fields of interest) is followed by the non-uniqueness of the
solution for the Upper scale statement!
Followed by the non-uniqueness of solutions for the Lower scale
statements!
Followed by the non-unique determination and simulation
for the "effective" coefficients!
Authors apparently do not realize this.

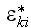 tensor, "effective" stress
tensor, "effective" stress

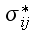 tensor, and other "effective"-like properties is that researchers while taking
averaging (mean) functions just cut out them from the real heterogeneous
physics and proper averaging mathematics.
tensor, and other "effective"-like properties is that researchers while taking
averaging (mean) functions just cut out them from the real heterogeneous
physics and proper averaging mathematics.
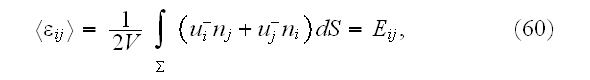

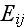 is the assigned macroscopic strain tensor, because generally
is the assigned macroscopic strain tensor, because generally
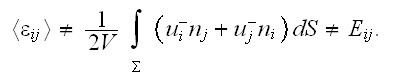

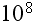 and more cycles) lifetime."
and more cycles) lifetime."
*********************
Excerpts from (Kushch et. al (2008a)):
In page 5103 in the abstract one can find that:
"The paper addresses the problem of calculation of the local stress field and effective elastic properties of a unidirectional fiber reinforced composite with anisotropic constituents. For this aim, the representative unit cell approach has been utilized. The micro geometry of the composite is modeled by a periodic structure with a unit cell containing multiple circular fibers. "
" Exact expressions for the components of the effective stiffness tensor have been obtained by analytical averaging of the strain and stress fields."
In page 5106 one can find that:
"Recently, an analytical method was developed by Kushch et al., (2005) and an accurate solution has been obtained for a finite array of elliptic fibers embedded into an infinite matrix. The method is based on the properly taken sets of outer and inner potentials and the relevant re-expansion formulae providing an efficient reduction of the initial BVP to the linear algebra problem. As shown below, this method, with some modefications, is appropriate for the problem under consideration."
Our comments 1:
This method of final array of elements
in composites should be recognized as an incorrect one, when this solution is
used for the Upper scale generalization, as it is done usually. Not only in
this work.
The reason for this argument is based on the idea that the transfer to the
Upper scale fields should be done with the mathematics of HSP-VAT, which is
the only correct one at this moment for scaled. heterogeneous local-nonlocal
physics.
More of that:
a) the set of inclusions is of the final quantity, meanwhile the results are
being expanded to the second scale without concern that the BC are different
at the Lower scale than at the Upper one if we consider that the problem is
the same, only the scale of physical modeling is different, right?
b) this trick is the one that used in homogeneous CM (HCM) as one of the
arguments to avoid consideration of the second Upper scale - mostly we have to
talk on the Upper scale modeling and simulation, because the Top-Down sequence
in CMH is not the area of apprehension yet.
In page 5107 one can find that:
"The fibers non-overlapping
condition is

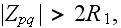 where
where

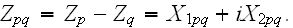 In the framework of the exposed method, considering the case of polydisperse
and multiphase composite is rather straightforward and does not meet any
problems. The conditions in the remote points and at the interface are the
same as in the previous problem, Eq. (17):
In the framework of the exposed method, considering the case of polydisperse
and multiphase composite is rather straightforward and does not meet any
problems. The conditions in the remote points and at the interface are the
same as in the previous problem, Eq. (17):
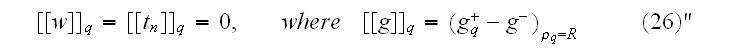
Our comments 2: this is the BCs at the Lower scale variables. Their consideration and effects are almost missing or wrong in the homogeneous treatments of the Ht problem.
In page 5108 one can find that:
"The fiber whose edges are shown in Fig. 1 by dashed line do not belong to the
cell while occupying a certain area within it. Thus, geometry of the unit cell
is given by its length

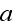 ,
height
,
height

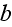 and the coordinates
and the coordinates

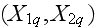 defining
the center of q-th fiber,
defining
the center of q-th fiber,

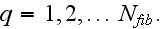 The entire composite is obtained by translating the cell along two orthogonal
directions.... "
The entire composite is obtained by translating the cell along two orthogonal
directions.... "
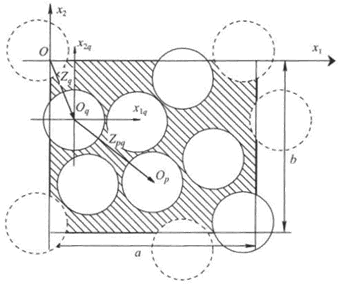
Our comments 3:
As it is one of the critical points
in the mathematical statement in HSP-VAT, we should be quite aware, that this
action of exclusion of few fibers that are parted between the selected REV and
the surrounding media has been done for a purpose. And the aim of this
exclusion is to use the Gauss-Ostrogradsky theorem (GOT) instead of the
Whitaker-Slattery-Anferson-Marle theorem (WSAMt) while the latter
is the only correct
way for integration. We show this down the road during our analysis.
We already have shown this trick by Dr. Kushch (apparently) performed in the
other science - the Thermal Physics paper (applicable to
electrostatics as well) analyses-review can be seen in -
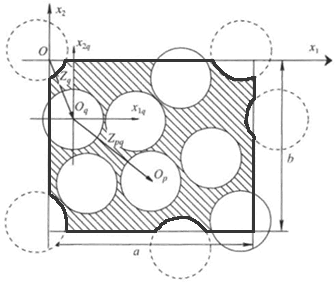
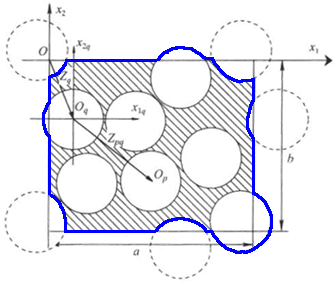
The reason for doing this - is that in any way, as we see in the our picture
presenting the real REV selected by authors and hidden in the Fig. 1 the part
of the REV outlined surface
The two phases interface surfaces of the REV are
Both surfaces equal to
If one would hide or neglect these features - then the GOT can be applied! The things with that is that the REV simulation is only the part of the Upper scale solution. And the one still REV is not enough to simulate many characteristics and the GE of the Upper (nonlocal) scale! All of that is usually done as in any Homogeneous science by using the basic spatial theorems to derive governing equations, dependencies. For solving them to know the problem.
The same is and for the Upper scale nonlocal GE for Ht Elasticity, the WSAM theorems should be used.
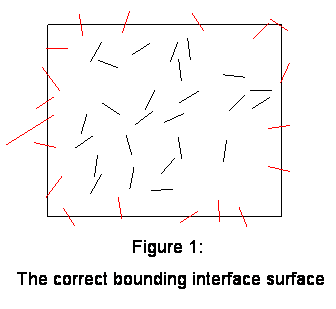
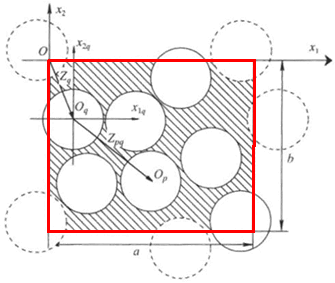
The vague kind of REV drawn in Fig. 1
does not let to have a clear picture - What is the REV here?
That can be imagined as the REVmin drawn in Figure below that is not overcoming seems the volume drawn in the previous figure -
After some attention to the verbal and graphical features in the paper
one can come up with the REV meant by authors -
It is pretty interesting to note again here that ALL FEATURES THIS TRICK was done for and actually mean that the ANY FREE SHAPE matrix phase intersection REV as might be the one depicted below is accepted and give the same result as the REV drawn above by Kushch and co-authors
We had pointed on this special and Wrong REV drawing mode in our review of Kushch (1997a) few years ago in
The correct, one of the regular shape (it can be of variety of shapes) REV for problems like this by Kushch et al. (2008a) is depicted below
anyone can notice that the bounding REV surface is intersecting actually the both phases.
This is the concept, one of the basic initial rules in HSP--VAT. You can draw freely the REV of any shape.
But that REV should be the same when the averaging is being assessed throughout the Lower scale (local) to deliver the Upper nonlocal scale fields. When REV is moving along any path, in any direction - do the integration over the same REV.
Then someone has the trully Averaged field.

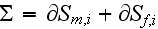 consists of the two surfaces. One is the matrix cutting surface
consists of the two surfaces. One is the matrix cutting surface

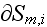 - input and output for fields fluxes, displacement field via the matrix;
another one is the surface cutting the fibers
- input and output for fields fluxes, displacement field via the matrix;
another one is the surface cutting the fibers

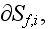 and the cutting should be involved in any REV because of the nature of the
problem.
and the cutting should be involved in any REV because of the nature of the
problem.

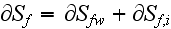 for fiber phase, where
for fiber phase, where

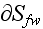 is the within the REV interface of the fibers; and
is the within the REV interface of the fibers; and

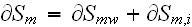 where
where

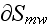 is the interface for matrix within the REV.
is the interface for matrix within the REV.

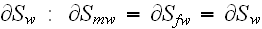 where
where

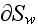 is the notation what is used in the HSP-VAT usually for this kind of interface.
is the notation what is used in the HSP-VAT usually for this kind of interface.

Further in this page one can read that:
"The stress field in the composite bulk is assumed to be macroscopically
homogeneous, which means constancy of the volume-averaged, or macroscopic,
strain

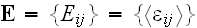 and stress
and stress

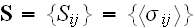 tensors, where
tensors, where

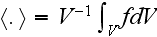 and
and

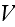 is the cell volume."
is the cell volume."
Our comments 4:
In the HSP-VAT these
brackets

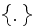 mean intrinsic phase averaging
mean intrinsic phase averaging

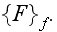 And again we need to recognize that these variables
And again we need to recognize that these variables

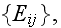

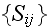 as
defined here, when applied to the two-phase medium under investigation do not
determine the real Upper scale (second scale nonlocal) strain
as
defined here, when applied to the two-phase medium under investigation do not
determine the real Upper scale (second scale nonlocal) strain

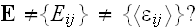 and stress
and stress

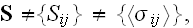 because what is assigned in the far away homogeneous medium - apart of the
studied two-phase medium domain, as done in the present work and numerous
others, does not automatically recognised as equal to the variables,
parameters that are just being averaged as the local variables. That is the
HSP-VAT conclusion determined long ago.
because what is assigned in the far away homogeneous medium - apart of the
studied two-phase medium domain, as done in the present work and numerous
others, does not automatically recognised as equal to the variables,
parameters that are just being averaged as the local variables. That is the
HSP-VAT conclusion determined long ago.
In page 5111 authors for evaluation of the Upper scale properties use notations as:
"On the other hand, the strain and stress fields given by this solution can be
integrated analytically to get the exact closed form expression for the
macroscopic, or effective, stiffness tensor

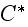 defined by
defined by
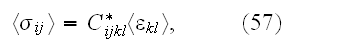
where

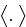 means averaging over the RVE (REV actually). In the problem we consider, the
stress field is macroscopically homogeneous and governed by the strain tensor
means averaging over the RVE (REV actually). In the problem we consider, the
stress field is macroscopically homogeneous and governed by the strain tensor

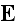 .
Also, RVE coincides with the cell volume and, due to the structure
periodicity,
.
Also, RVE coincides with the cell volume and, due to the structure
periodicity,
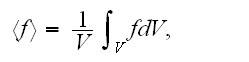
where

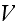 is a cell volume. In our case,
is a cell volume. In our case,

 (unit length is assumed in z-direction)."
(unit length is assumed in z-direction)."
In page 5112 one can find continuation of that definition:
"To evaluate

 ,
we write
,
we write
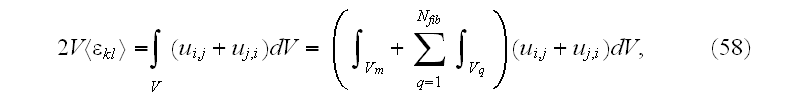
where

 is the volume of the pth fiber and
is the volume of the pth fiber and

 is the matrix volume inside the cell:
is the matrix volume inside the cell:

 Applying the Gauss' theorem leads to
Applying the Gauss' theorem leads to
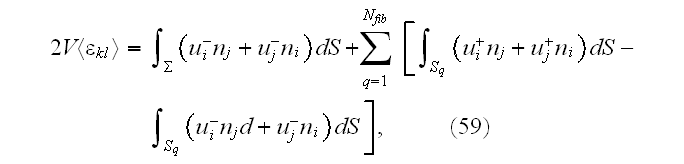
where

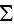 is the cell outer surface and
is the cell outer surface and

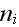 are the components of the unit normal vector. Taking into account the first
condition (51) and decomposition
are the components of the unit normal vector. Taking into account the first
condition (51) and decomposition

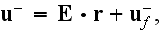 we get
expectedly
we get
expectedly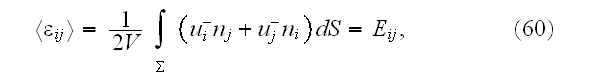
i.e.

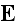 has a meaning of the macroscopic strain tensor. Hence, all components of the
effective stiffness tensor
has a meaning of the macroscopic strain tensor. Hence, all components of the
effective stiffness tensor

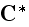 can be determined from (57) as
can be determined from (57) as

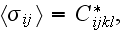 where the stress field corresponds to the macroscopic strain
where the stress field corresponds to the macroscopic strain

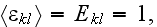

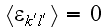 for
for

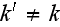 and
and

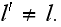
The macroscopic stress tensor can be written in the following form
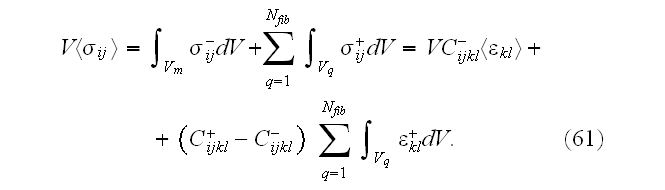
Therefore, we need to integrate the strains over the fiber volume only. By
Gauss' theorem, integrals in (57) are reduced to
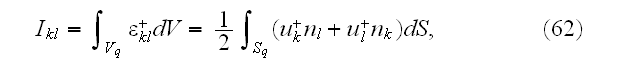
which we can obtain analytically."
Our comments 5:
In this the only section of the paper
devoted to an attempt to address the averaged (Upper) scale characteristics of
the problem we just need to debacle on these formulae (58), (59) that are like
cheating on the integration, because used the GOT instead of correct WSAM
theorem.
Well, we say it again that the proper usage of the GOT might bring
the singled out correct value at the Lower scale and
formulae for a special artificial configuration - which does not
state averaged solution at the Upper scale in any way,
meaning it does not explain or state the Upper scale nonlocal mathematical
statements including the governing equations - GEs and solution
for the Upper scale phenomena fields.
And Dr. Kushch knows on that difference since 1994.
In the expression
In the formula (60) should be used the both phases strain tensor.
The formula (61) is incorrect one because
Doing this along with the hidden definition of the used REV is a cheating on readers and themselves - because by hiding the Upper scale nonlocal concepts and coefficients definitions (well, even if authors, but Kushch himself, are not familiar with this science) deprive authors, readers and the funding agencies the proper treatment of the heterogeneous problems. See our summary and conclusions above for Kushch et al. (2009).
The formula (62) is incorrect one because used the GOT instead of correct WSAM
theorem.

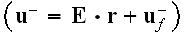 is involved the Scaleblending of the different
scales variables.
is involved the Scaleblending of the different
scales variables.

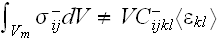 is the trick done because by doing this with the help of assigned
is the trick done because by doing this with the help of assigned

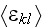 these and other authors making the Upper nonlocal scale stress assessment dependent only on the inclusion phase simulation! And by doing this authors actually forcefully assign the
macroscopic features, up to a solution for the matrix scale (mostly).
these and other authors making the Upper nonlocal scale stress assessment dependent only on the inclusion phase simulation! And by doing this authors actually forcefully assign the
macroscopic features, up to a solution for the matrix scale (mostly).
1) To the given Comments to this paper misconducts the summary can be used the same as for the above publication - Kushch et al. (2009).
1) The same homogeneous approach by Dr. Kushch as demonstrated in his and his co-authors works on heterogeneous tasks brings the same kind of disaster to the Upper scale assessments simulation. They can not do this - by using the incorrect tools.
I told to Dr. Kushch many times on that in 1994-1997. Unfortunately, as can be said - the personal egos prevail in almost everything.
*********************
Excerpts from Kushch et. al (2008b):
In page 2758 in the abstract one can find that:
"The primary goal of this work is to develop an efficient analytical tool for the computer simulation of progressive damage in the fiber reinforced composite (FRC) materials and thus to provide the micro mechanics-based theoretical framework for a deeper insight into fatigue phenomena in them. An accurate solution has been obtained for the micro stress field in a meso cell model of fibrous composite.
......By averaging over a number of random structure realizations, the statistically meaningful results have been obtained for both the local stress and effective elastic moduli of disordered fibrous composite. A special attention has been paid to the interface stress statistics and the fiber debonding paths development, which appear to correlate well with the experimental observations."
Our comments: As we will see this is the same homogeneous treatment - very good for the Lower scale with that one phase assignment, but is a complete failure when authors seeking the generalization of their Lower scale results into the Upper scale characteristics.
In page 2759 one can find from the review of predecessors work:
"In the comprehensive review by Degrieck and Van Paepegem (2001), the progressive damage models which use one or more damage variables related to measurable manifestations of damage (interface debonding, transverse matrix cracks, delamination size, etc.) have been claimed as the most promising ones because they quantitatively account for the damage accumulation in the composite structure.
The gradual deterioration of a FRC - with a loss of stiffness in the damaged zones - leads to a continuous redistribution of stress and a reduction of stress concentrations inside a structural component (e.g., Allen et al., 1990; Shokrieh and Lessard, 2000; Degrieck and Van Paepegem, 2001). Hence, prediction of the final state of the composite structure requires simulation of the complete path of successive damage states. In order to provide an adequate description of progressive damage with account for the local stress redistribution, one needs to use a complicated structure model, able to reflect both the micro structure statistics and the local damage events."
"....The composites of primary interest for us are the unidirectional glass
fiber - epoxy matrix FRC's. The pre-requisite of using these materials in the
wind turbine components is extremely high
(~
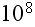 and more cycles) lifetime."
and more cycles) lifetime."
".....The approximate multi-particle effective field method (MEFM) is used which allows to estimate the second statistical moments of stresses in both the constituents and the interfaces between the matrix and fibers and thus predict the effective envelope for failure initiation.
However, MEFM does not provide evaluation of local stress fields in the constituents and at the interfaces."
Our comments: These correct evaluations of the one scale - Lower scale, modeling and simulation techniques can have the basis for present authors, at the same time, do the incorrect evaluation of the second scale properties of the composite.
In page 2760 one can find that on the methods used for the Lower scale solutions:
"Even more numerically efficient version of MEM (Golovchan et al., 1993; Kushch, 1997, among others) utilized the series expansion of displacement vector over a set of appropriate periodic singular solutions. In this case, the matrix coefficients are expressed in terms of the easy-to-calculate sums and the only remaining problem is to find an efficient way to solve the resulting set of linear equations. "
"....Recently, the very efficient solving techniques have been developed based
on the fast multipole method (Greengard, 1994; Sangani and Mo, 1996; Kushch et
al., 2002; Wang et al., 2005b, among others). In this and similar advanced
though rather involved algorithms, a computational effort scales as

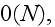 where
where

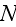 is a number of inclusions per cell, which makes it rather efficient for
studying the very large models (say, with
is a number of inclusions per cell, which makes it rather efficient for
studying the very large models (say, with

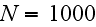 and more), often used in the fluid suspension mechanics in order to account
for the long-range interactions accurately. In the solid composites no such
long-range interactions exist, and a number from 100 and 200 fibers per cell
was reported by many authors as quite sufficient to provide the statistically
meaningful results. "
and more), often used in the fluid suspension mechanics in order to account
for the long-range interactions accurately. In the solid composites no such
long-range interactions exist, and a number from 100 and 200 fibers per cell
was reported by many authors as quite sufficient to provide the statistically
meaningful results. "
".....In the present work, an analytical approach by Golovchan et al., (1993) has been further developed and applied for studying the local stress and the effective elastic properties of FRC composite using the meso cell model."
Our comments:
Amidst the description of the variety
of mathematical approaches used for solution of the Lower scale heterogeneous
problem authors writes that "and the effective elastic
properties of FRC composite using the meso cell model" - this is really
a stretching.
This is the claim that the averaging over the REV would help to find the Upper
nonlocal characteristics. That is the way Kushch had assignments
for simulating
Heterogeneous test problems in the HSP-VAT Thermal Physics and Fluid Mechanics
in 94-97. Unfortunately, he does this here with co-authors using the Lower
scale homogeneous methods and thus they failed to achieve that goal using the
REV defined Lower scale local solution.
In page 2761 one can find that the critical definition of the REV (authors used the "internal" self-invented term RUC):
"The fibers whose edges are shown in Fig. 1 by dashed line do not belong to
the cell while occupying a certain area within it. Thus, geometry of the unit
cell is given by its length

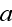 ,
height
,
height

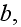 the coordinates
the coordinates

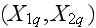 being
the centers of inclusions
being
the centers of inclusions

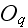 and their radii
and their radii

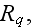

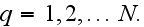 The whole composite bulk can be obtained by translating the cell in the two
orthogonal directions."
The whole composite bulk can be obtained by translating the cell in the two
orthogonal directions."
"Number N of the fibers with centers inside the cell can be taken large sufficiently to simulate micro structure of an actual disordered composite. In the considered model, a diameter and the elastic moduli are defined individually for each separate fiber. It provides applicability of this model for studying the multi-component systems and the effect of fiber diameter scattering, which can be quite considerable even in the commercial FRCs, ...."
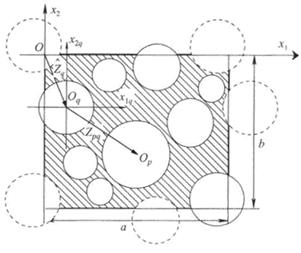
Our comments: The same vital in consequences definition of the REV shown in the figure and of the real hidden volume as we noted in the above analysis of Kushch et al. (2008a).
In page 2763 one can find the interface BC and averaging conditions that are wrong:
"At the matrix-fiber interfaces, the perfect bonding conditions are
prescribed: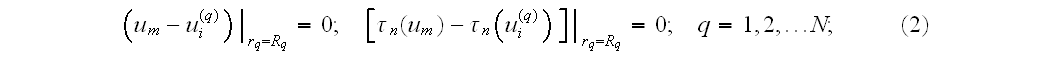
where

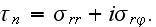
The stress field in the composite bulk is assumed to be macroscopically
homogeneous, which means constansy of the volume-averaged, or macroscopic,
strain

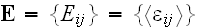 and stress
and stress

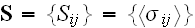 tensors, where
tensors, where

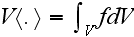 and
and

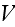 is the volume of meso cell."
is the volume of meso cell."
Our comments:
Practically the same equations and
definitions as in Kushch et al. (2008a).
And the averaging equalities are wrongly written because authors do not use
(but Kushch was familiar with HSP-VAT) the correct means for averaged
properties in composites.
In page 2764 one can find the BC for the REV:
"Next, it is of common knowledge that under macroscopic stress homogeneity
condition periodicity of structure results in periodicity of relevant physical
fields. In our case, the periodicity
condition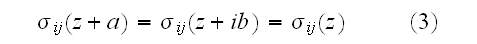
can be alternatively regarded as the cell boundary condition providing continuity of the displacement and stress fields between the adjacent cells."
Our comments:
these BCs are incorrect for the
two-scale heterogeneous problems (physics), because of the two reasons:
1) is as for the HSP-VAT assessments;
2) because of the 2-nd scale BCs that should be satisfied.
In page 2764 further one can read on the method of solution:
"The theory we apply to study this problem is the Kolosov-Muskhelishvili's method of complex potentials, widely recognized as the powerful analytical technique for a given class of problems. However, unlike the case of a finite array of inclusions (Buryachenko and Kushch, 2006; Mogilevskaya and Grouch, 2001), periodicity of the model implies introducing the appropriate periodic complex potentials. The computational cost-efficient way to build up solution of the model BVP in the class of periodic (rather than doubly periodic) functions has been suggested by Golovchan et al. (1993); a brief summary of the theory of periodic potentials is given in Appendix A."
In page 2770 one can find the models for the second Upper scale:
"3.2 Effective stiffness
The stress field obtained from the above solution can be integrated
analytically to get the closed form exact expression of the macroscopic, or
effective, stiffness tensor

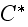 defined by
defined by
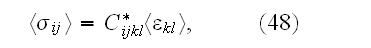
where

 means averaging over the RVE (REV actually-our comment
). In the model we consider, RVE coincides with the meso cell and, due to
periodicity of
structure,
means averaging over the RVE (REV actually-our comment
). In the model we consider, RVE coincides with the meso cell and, due to
periodicity of
structure,
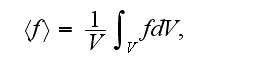
where

 is a cell volume. In our case,
is a cell volume. In our case,

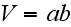 (unit length is assumed in
(unit length is assumed in

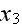 -direction)."
-direction)."
Our comments:
wrong definition of

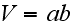 as long as authors excluded from the
as long as authors excluded from the

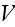 some boundary fibers while, at the same time, any boundary for the matrix
phase can be accepted - see the comments, summary and conclusions to the
Kushch et al. (2009) above. Nevertheless, the definition of REV's volume
should include definition of the both phases exactly.
some boundary fibers while, at the same time, any boundary for the matrix
phase can be accepted - see the comments, summary and conclusions to the
Kushch et al. (2009) above. Nevertheless, the definition of REV's volume
should include definition of the both phases exactly.
In page 2770 we see the continuation of basic definitions:
"In the problem we consider, the stress field is macroscopically homogeneous
and governed either by the constant macroscopic strain tensor

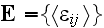 or
stress
or
stress

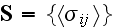 tensor.
To evaluate
tensor.
To evaluate

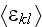 ,
we write
,
we write
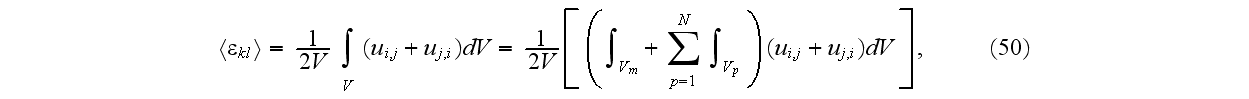
where

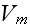 is the matrix volume inside the cell and
is the matrix volume inside the cell and

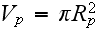 is the volume of the pth fiber:
is the volume of the pth fiber:

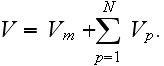 Now, we apply the Gauss' theorem to reduce the volume integrals to surface
ones: taking into account also the first of adhesion conditions (2) we get
Now, we apply the Gauss' theorem to reduce the volume integrals to surface
ones: taking into account also the first of adhesion conditions (2) we get
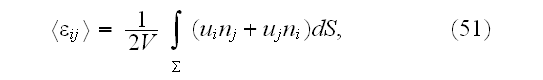
where

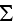 is the cell outer surface and
is the cell outer surface and

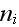 are the components of the unit normal vector."
are the components of the unit normal vector."
Our comments:
Here is the same comments to these
formulae - wrong formulae (51) can not be put in here - see the comments to
the same formulae in Kushch et al. (2008a) above. The reason to cheat on the
boundary specific is might be for reason of not to disclose the existing WSAM
theorems regarding this matter and their consequences for the Upper scale
averaging.
Also, the REV outlined surface
Meanwhile, this surface
The two phases interface surfaces of the REV are
Both surfaces equal to

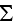 is not specified here?
is not specified here?

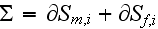 consists of the two surfaces. One is the matrix cutting surface
consists of the two surfaces. One is the matrix cutting surface

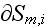 - input and output for fields fluxes, displacement field via the matrix;
another one is the surface cutting the fibers
- input and output for fields fluxes, displacement field via the matrix;
another one is the surface cutting the fibers

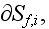 and the cutting should be involved in any REV because of the nature of the
problem.
and the cutting should be involved in any REV because of the nature of the
problem.

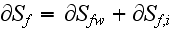 for fiber phase, where
for fiber phase, where

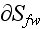 is the within the REV interface of the fibers; and the
is the within the REV interface of the fibers; and the

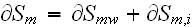 where
where

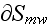 is the interface for matrix within the REV.
is the interface for matrix within the REV.

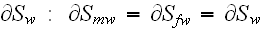 where
where

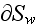 is
the notation what is used in the HSP-VAT usually for this kind of interface.
is
the notation what is used in the HSP-VAT usually for this kind of interface.
In page 2771 we see the continuation of basic definitions:
"Evaluating the macroscopic stress tensor follows the same way:
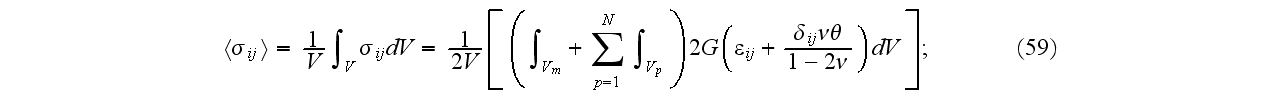
after some algebra, we came to
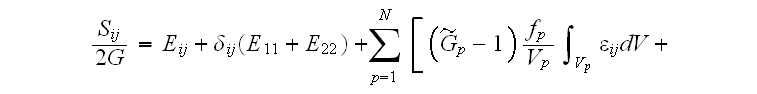
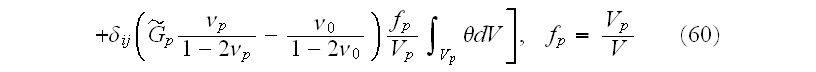
Thus, the problem is reduced to evaluating the
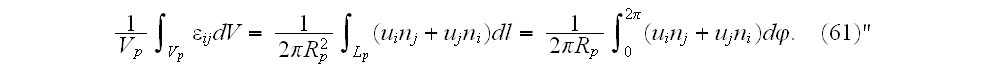
Our comments:
We have to comment with almost the
same remarks as for the previous study by Kushch et al. (2008a). These
averaging of strain and stress formulae (59)-(61) are incorrect - see the
above notes.
Besides, the REV'S outlined surfaces are not the boundaries
where we can have the assigned boundary values!? That is because the
macroscale major characteristic as
That the numerical simulation of even the Lower scale elasticity problem is
incorrect - because of usage the macroscopic bulk composite assigned strain
for the matrix averaged quantity without specifics of Heterogeneous fields
averaging, and vise versa the Upper scale assessments are incorrect because
the science of homogeneous elasticity theory is incorrect when applied to this
kind of Heterogeneous two-scale problems seeking the Upper scale properties by
just application of the homogeneous media GOT.

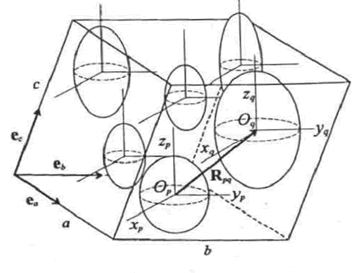
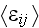 which is being assigned in each problem by Dr. Kushch - to get somehow the
values of the field nonlocal displacement and strain need being accounted with
GOT or WSAM theorem as the already known ones.
which is being assigned in each problem by Dr. Kushch - to get somehow the
values of the field nonlocal displacement and strain need being accounted with
GOT or WSAM theorem as the already known ones.
1) Some of the comments to this publication detail must be considered as the additional summary to those outlined in the Kushch et al. (2009).
1) We came to the needed point by point analysis with regard of the homogeneous treatment of heterogeneous problems when the scaled (two-scale) structure-properties relations are at stake, and have to be obtained as such, but unreachable for homogeneous community workers.
The result of analysis is unfortunate for that kind of frivolous mixing of the physics and math for HtCM that performing as "strictly justified" by numerous HCM micro-communities including Dr. V.Kushch and his co-authors.
2) We have developed these HSP-VAT physical modeling and mathematics fundamentals for the Heterogeneous media Elasticity theory (HtEt), Continuum Mechanics scaled statements and simulation, that needs to be applied in all Dr. Kushch's studies.
*********************
Excerpts from Kushch (1997):
In page 1353 in the abstract one can find that:
"......Analytical averaging of the strain and stress tensors gives the exact expressions for all components of effective elasticity tensor of composite considered. The influence on stress concentration and effective moduli of the structural parameters of composite is investigated and the comparison is made with known approximate solutions."
Our comments: The errors started here in the abstract. As we will see the same homogeneous tools were applied to the Heterogeneous problem with the claim that the averaged Upper scale characteristics were simulated and calculations were done with the high accuracy. This study was the beginning of the Kushch's becoming the gatekeeper for the HSP-VAT and the future Wheel re-inventor for the scaled, local- nonlocal heterogeneous elasticity theory and Continuum Mechanics as a whole since 1994.
In page 1354 one can find that:
"We do not suppose the whole inclusion to be lying completely inside the cell. Intersection of the inclusions with the sides of a parallelepiped is possible; the only requirement is that the centers of inclusions do not lie on the boundary of the cell." ?
Our comments: Here is the certain restriction about the localization of the particles and the boundary of the REV. Nevertheless, this is the full scale REV defined and we should expect even with this artificial restriction the corresponding correct averaging procedures following the WSAM theorem. See our Conclusions to the Kushch et al. (2009) on that issue.
It won't happen. The GO theorem will be used in this work instead.
In page 1355 one can find that:
After presenting the common knowledge Homogeneous elasticity theory GE for each phase - particles and the matrix combined always, author writes:
"We suppose that the stressed state of a composite medium is induced by the
remote constant strain tensor

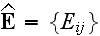 prescribed. The displacement vector
prescribed. The displacement vector

 in each phase of the composite satisfies the Lame's
equation
in each phase of the composite satisfies the Lame's
equation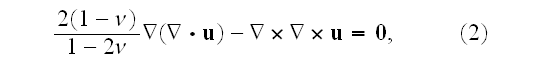
where

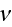 is the Poisson's ratio;
is the Poisson's ratio;

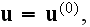

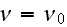 in the matrix,
in the matrix,

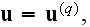

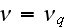 in the particle of the qth kind."
in the particle of the qth kind."
"On interfacial surfaces the continuity conditions of the displacement vector

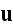 and normal stress
tensor
and normal stress
tensor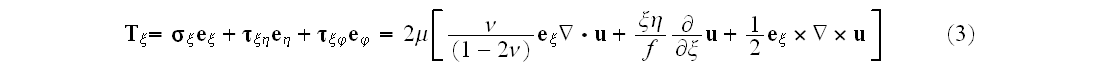
are
prescribed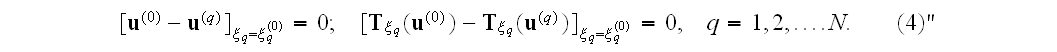
"As it is easy to prove, due to the periodicity of the structure, the solution also has periodicity features. So, the displacement vector in a continuum phase (matrix) can be presented as a sum of the linear far field and the periodic disturbance field caused by the presence of inhomogeneities:
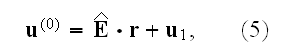
where
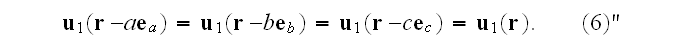
"It was shown elsewhere (e.g. Kushch, 1985; Sangani and Lu, 1987) that in this
case the tensor

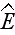 has a sense of the average strain tensor of the composite,
i.e.
has a sense of the average strain tensor of the composite,
i.e.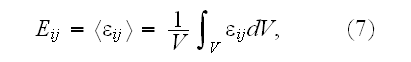
where

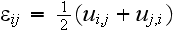 and
and

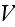 is the representative volume of the composite. Taking into account eqns (5)
and (6), the periodicity unit (Fig. 1) may be chosen as a representative
volume. Also it follows from eqn (6) that the satisfaction of contact
conditions (4) for the particles with centers lying inside the
structure cell means their equal satisfaction for the rest of
inclusions in a medium.
is the representative volume of the composite. Taking into account eqns (5)
and (6), the periodicity unit (Fig. 1) may be chosen as a representative
volume. Also it follows from eqn (6) that the satisfaction of contact
conditions (4) for the particles with centers lying inside the
structure cell means their equal satisfaction for the rest of
inclusions in a medium.
Thus, the problem here is to construct the solution of eqn (2) satisfying the periodicity conditions (5) and (6), and the interfacial conditions (4). "
Our comments:
Author uses the known from HSP-VAT term here - "representative
volume", and the statement that the remote constant strain tensor

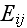 is equal to the nonlocal averaged two-phase strain value.
That might be as well, but only if the nonlocal averaged two-phase strain
is derived and formed correctly, that is not the case for this author
treatment.
Meanwhile, in the
further deliberations one would learn that the assigned strain greatly helped
to make the pseudo-averaging over the total medium, which is the real
reason to assign
the macroscopic strain tensor. And that is also leads to the open box of
errors we spoke above.
is equal to the nonlocal averaged two-phase strain value.
That might be as well, but only if the nonlocal averaged two-phase strain
is derived and formed correctly, that is not the case for this author
treatment.
Meanwhile, in the
further deliberations one would learn that the assigned strain greatly helped
to make the pseudo-averaging over the total medium, which is the real
reason to assign
the macroscopic strain tensor. And that is also leads to the open box of
errors we spoke above.
In page 1356 one can find the method of analytical solution:
"The analytical method applied here to solve the boundary-value problem (2) - (6) is, in fact, the modified variant of the approach used by Kushch (1995b) to solve the elasticity problem for a medium containing a finite number of aligned spheroidal inclusions. The essence of the method, in few words, is the representation of the displacement vector in a multiply-connected region by a series of partial vectorial solutions of Lame's equation, and use of additional theorems for these solutions to reduce the boundary-value problem to an infinite set of linear algebraic equations."
Our comments:
That means the Lower scale local
solution of the two-phase elasticity problem can be done analytically and with
a high accuracy.
Meanwhile, we need to mention again - that this solution is
the one that is determined by local point fields and with adjusted usage of
the Upper scale assigned one of the main characteristics. That the usually
meant the homogeneous media averaging is going to produce just the one of
infinity of nonlocal fields.
In page 1358 one can find the usual homogeneous method for Averaging of the local fields to obtain the nonlocal properties for this problem:
"The solution obtained is sufficient for the calculation of the four-rank
tensor

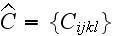 of the effective elastic moduli defined by the
relation
of the effective elastic moduli defined by the
relation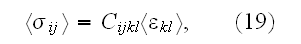
where

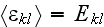

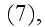
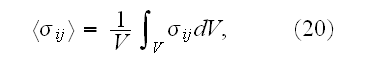

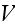 is the volume of elementary structure cell (Fig. 1). Hence, for determination
of
is the volume of elementary structure cell (Fig. 1). Hence, for determination
of

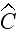 it is sufficient to find the expression for
it is sufficient to find the expression for

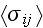 and calculate them for the corresponding values of
and calculate them for the corresponding values of

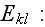
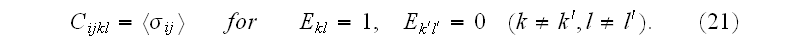
By the use of Hooke's law for the material of each composite phase we have
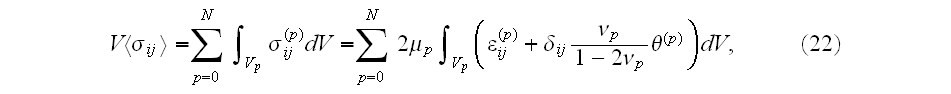
where

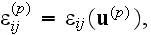

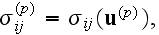

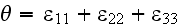 and
and

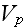 is the volume of the
is the volume of the

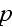 th
phase within the elementary cell, equal in total to the volume of the
th
phase within the elementary cell, equal in total to the volume of the

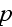 th
inclusion. Thus
th
inclusion. Thus
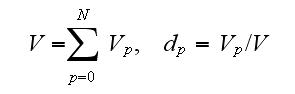
is the volume fraction of the

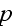 th
phase. The equality (22) may be rewritten in the following
form
th
phase. The equality (22) may be rewritten in the following
form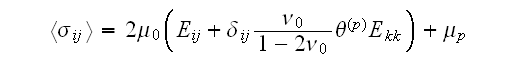
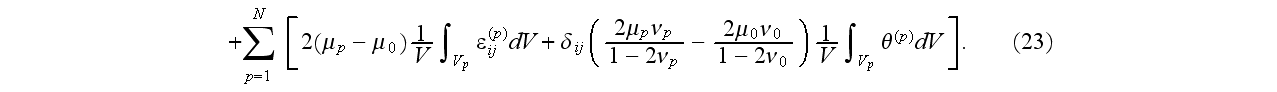
Hence, we need to integrate strains over the volume of inclusions only. With
the aid of Gauss' theorem the volume integrals are reduced easily to surface
ones: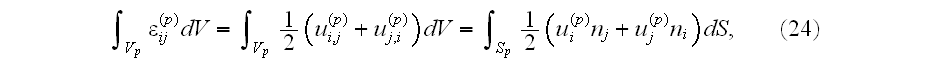
where

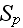 is the surface
is the surface

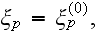

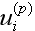 and
and

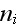 are the Cartesian components of displacement vector
are the Cartesian components of displacement vector

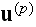 and of unit vector
and of unit vector

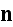 normal to this surface, respectively."
normal to this surface, respectively."
Our comments:
We have to comment with almost the same
remarks as for the analyzed previous studies by Kushch et al. (2009),(2008a),
(2008b). These averaging of strain and stress formulae (22)-(24) are incorrect
- see the above notes.
That the numerical simulation even of the Lower scale elasticity problem is
incorrect - because usage of the macroscopic bulk composite assigned strain
which actually meaning the macroscale value assigned for any ratio and values
of elasticity moduli at the Lower scale? Top-Down
assignment of physical Conditions? While
the Upper scale assessments are incorrect because the averaged assessments of
homogeneous elasticity theory are incorrect when applied to this kind of
Heterogeneous two-scale problems.
These averaging procedures are incorrect not only because used the GOT instead
of correct WSAM theorem. They are incorrect also because there were no Upper
scale averaged equations that would enforce the different understanding of
the averaged governing equations and fields, different treatment and
simulation results.
1) This is the one of two (or more) papers that Dr. Kushch published in 1997 and while already being completely aware that these treatments of the averaged characteristics as done in the Homogeneous Elasticity theory are incorrect.
Nevertheless, he preferred to stay with the one scale homogeneous CM followers and became the gatekeeper for the heterogeneous Elasticity Mechanics.
2) Throughout the last ~ 15 years Dr. Kushch silently has been using few rules of the HSP-VAT and trying to stay with the Lower one scale homogeneous statements in elasticity theory. Anyway, he needs to develop each time some averaged characteristics by the nature of his and of his co-authors subject matter.
He lost a lot in this course and we reviewed these incorrectness' and explained in a simple available to grad students language what are those.
He is slowly moving to the area of Wheel Re-Inventors with his last years studies. In the next ~ twenty years Dr. Kushch would realize how much time and effort he had placed onto himself for no good reason and output. His results will be redone within the HSP-VAT.
Welcome to personal rediscovery of the HSP-VAT for the Ht Elasticity Theory. It has been done already, but anyway welcome.
3) We have developed these HSP-VAT physical modeling concepts and mathematics for the Heterogeneous media Elasticity theory (HtEt), Continuum Mechanics scaled statements and simulation, that needs to be applied in all Dr. Kushch's studies.
Why from UCLA? This kind of workers spread all over the world. Well, that is just because the 12 years and numerous contacts with them regarding their "wrongdoings" were useless and they knew what is going on in the field - as soon as I was affiliated with the MAE department for 12 years.
The only one professor was demonstrating the full support and helped me with promotion of
the scaled, hierarchical agenda at the department - professor I.Catton, very known for his input
in the numerous areas of Thermal Physics and Fluid Mechanics.
Since my departure from UCLA MAE department he has been trying to maintain some
level of flame in the local hotbed of HSP-VAT, back then simply the VAT
as I named the field at the beginning of the 90s. Unfortunately,
the educational base at the department for HSP-VAT is absent because the
faculty did not want to let me establish the program on scaled physics,
mechanical engineering at the department in the 90s and later.
That is why, that source of application of HSP-VAT, mostly in mechanical
engineering is dying or already dead.
Now I.Catton tries to present himself as the "founder" of HSP-VAT (VAT), without even naming me or consulting with me - Who is the founder of HSP-VAT? We did should respond to this claim as long as I was affiliated with his lab for 12 years and developed a lot of things over there. But saying that he is a "starter", or "founder" - it is too much. My reply to this claim and comments on the history of HSP-VAT are featured at the beginning of - "Announcements. Announcement #2:".
Another professor at MAE department - G.Pomraning, started in the 90s to footstep in the science of Nuclear Physics (Neutron Transport Theory (NTT), etc.) following the HSP-VAT developments in what was known as a linear processes averaging. Pomraning with co-authors started to recognize that the particle (neutron included) transport equations are actually allegedly accepted as averaged and in a few papers in the middle of the 90s they timidly gave another kind of radiative transport equation for a two-phase (biphasic, binary) medium.
In my paper (1999) on this topic where I introduced the VAT averaged, one of the options, for the upper scale phase averaged, radiative transport equation (VARE) - "Radiative Transport", this subject matter was only touched.
Other faculties when making study on heterogeneous, famous now "multiscale" topics - they waste the public money, pretending that they can do heterogeneous, multiscale studies. Or they should admit that their qualifications are not good enough to understand the mechanics and physics of HS media.
Unfortunately for myself and for my co-authors and colleagues at UCLA generally, and of MAE department, I need to say a word on most of "heterogeneous" like research and publications by MAE and other departments professionals. Few other departments also making themselves the targets for future mockery. Through the years we also tried to make professors at MAE department involved, but without success. These professionals, nevertheless, doing also the heterogeneous and fashioned lately "multiscale" media studies are wasting just their time and public money in a real sense.
They do the incorrect research; some publish incorrectly written books, for decades.
I have no other choice as to say and make obvious that speciaslists who could learn personally from me the proper, the only correct science, (sorry for the language, still I have no real obstacles saying this as I do this science for more than 25 years) for treatment of scaled, Multiscale, heterogeneous, hierarchical matter are doing things that are out of a real field. They play their wrong party and are looking for honored retirement. They teach students having the wrong scripts.
And that is bad for students, that is bad for science, that is bad and costly for industries, when people are doing their "string" theory in mechanics, physics for at least this generation, taking out the public money. Well, it is better than the string theorists hoping to do for a next thousand years? Still is too long for our kids being thankful to them for such an alchemistry.
Regarding professors N.Ghoneim and J.-S.Chen of MAE department, I wrote already on their kind of "multiscale" mechanics of heterogeneous media, they are in the web already -
Professors had a time after my departure from MAE, to look at the HSP-VAT and not waste time, money, and students' resources on pseudo-multiscaling, "nanoscaling" structures, that will not deliver something worthwhile.
Anyway, they also doomed to be the Wheel-Reinventors. There is no other fundamentals exist for doing Heterogeneous Scaled, Hierarchical physics than the HSP-VAT for more than 40 years. Correct fundamentals. They will need to use some elements of HSP-VAT and better sooner than later.
We are addressing these and close issues in our sections on Heterogeneous scaled media Continuum Mechanics, Elasticity theory, etc.; while with more detail and educational write-ups in the sub-section -
where we introduce the concepts, present also some correct formulae for problems published by Dr. V.Kushch and co-authors, by other mentioned here authors, as elements of the two-scale Heterogeneous Elasticity theory in the Bottom-Up direction, and give a notice of the Scaleportation for the Ht Elasticity, Viscoelasticity, Viscoplasticity, Heterogeneous Continuum Mechanics.
**********************************************************************
Well, this is pretty fresh and obviously good sample (slice, if we can say this) of the knowledge base and the fundamental tools used in the US, and not only in the US, industries (aerospace particularly) and academies for the Heterogeneous Scaled problems in Elasticity and CDM of composites particularly right now in 2000-2010.
The review refers to substantial number of publications and researches - all in the same mode of Homogeneous approach for the Heterogeneous problems. We almost done, better to say we've already done with the script of analytical notes on this work and preparing part of it for this website to be uploaded soon.
Here we read from research people in the industry. Some authors are affiliated with "Boeing", "Sikorsky Aircraft Corp." That means we get to know how academia and largest corporations support the ignorance in Heterogeneous Continuum Mechanics. In the long list of references - 164 refs., there are
Excerpts from Pindera et al. (2009):
*********************
The first author is the outstanding professional in Ukraine's national continuum mechanics field and simultaneously having a position of high status official in the Ukraine academic science bureaucracy (he is Director of a large Institution).
And the title of the paper is like they are the first to say the most important words of the groundbreaking knowledge on the subject?
So, we can expect to find the discussion from the Ukrainian science high rank official on issues of composites, nanocomposites and multiscaling, scale "bridging" for composites modeling, the analytical approaches to the scaling in composites, etc.
Excerpts from Guz et al. (2007):
In page ... in the abstract one can find that:
*********************
Cohen, I., Bergman, D.J., "Effective Elastic Properties of Periodic Composite Medium," J. Mechanics and Physics of Solids, Vol.51, pp. 1433-1457, (2003)
Drago, A., Pindera, M.J., " Micro-macromechanical Analysis of Heterogeneous Materials: Macroscopically Homogeneous vs Periodic Microstructures," Composites Science and Technology, Vol. 67, Iss. 6, pp. 1243-1263, (2007)
Eshelby, J.D., "The Elastic Field Outside the Ellipsoidal Inclusion," Proc. Roy. Soc. London, A252, pp. 561-569, (1959)
Gusev, A.A., "Representative Volume Element Size for Elastic Composites: a Numerical Study," J. of Mechanics and Physics of Solids, Vol. 45, pp. 1449-1459, (2002)
Guz, A. N., Rushchitsky, J. J., and Guz, I. A., "Establishing Fundamentals of the Mechanics of Nanocomposites," Int. Applied Mech., Vol. 43, No. 3, pp. 247-271, (2007)
...
Kushch, V.I., "Conductivity of a periodic particle composite with transversely isotropic phases," Proc. R. Soc. Lond., A 453, pp. 65-76, (1997a)
Kushch, V. I., "Microstresses and effective elastic moduli of a solid reinforced by periodically distributed spheroidal particles," Int. J. Solids and Structures, Vol. 34, Iss. 11, pp. 1353-1366, (1997b)
Golovchan, V.T., Guz', A.N., Kokhanenko, Yu.V., and Kushch, V.I., Mechanics of Composites. T.1. Statics of Materials, Kiev, Naukova Dumka, 1993, 455pgs, (in Russian)
Kushch, V.I. and Artemenko, O.G., "Determination of Temperature Field in a Granular Layer," Doklady AN Ukr. SSR, No. 3, pp.74-77, (1983), (in Ukrainian)
Kushch, V.I., "Stressed State and Elastic Moduli of a Periodic Composite Reinforced By Coated Spherical Particles," Mechanics of Composite Materials, Vol. 29, No. 6, pp. 816-822, (1993), (in Russian)
Kushch, V.I., "Heat Conduction in a Regular Composite With Transversely Isotropic Matrix," Doklady AN Ukr. SSR, No.1, pp.23-27, (1991), (in Ukrainian)
Kushch, V.I., "Thermal Conductivity of Composite Material Reinforced by Periodically Distributed Spheroidal Particles," Engng.-Phys. Journal, Vol. 66, 497, (1994), (in Russian)
Kushch, V.I, Sangani, A.S., "Stress Intensity Factors and Effective Stiffness of a Solid Containing Aligned Penny-Shaped Cracks," Int. Journal of Solids and Structures, Vol. 37, pp. 6555-6570, (2000a)
Kushch, V.I, Sangani, A.S., "Conductivity of Composite Containing Uniformly Oriented Penny-Shaped Cracks or Perfectly Conducting Disks ," Proc. Roy. Soc. London, A456, pp. 683-699, (2000b)
Kushch, V.I, Sangani, A.S., Spelt, P.D.M., and Koch, D.L., "Finite Weber Number Motion of Bubbles Through a Nearly Inviscid Liquid," J. Fluid Mech., Vol. 460, pp. 241 - 280, (2002)
Kushch, V.I., Sevostianov, I., and Mishnaevsky, L.Jr., "Stress Concentration and Effective Stiffness of Aligned Fiber Reinforced Composite with Anisotropic Constituents," Int. Journal of Solids and Structures, Vol. 45, No. 18-19, pp. 5103-5117, (2008a)
Kushch, V.I., Shmegera, S.V., and Mishnaevsky, L.Jr., "Meso Cell Model of Fiber Reinforced Composite: Interface Stress Statistics and Debonding Paths," Int. Journal of Solids and Structures, Vol. 45, No. 9, pp. 2758-2784, (2008b)
Kushch, V.I., Sevostianov, I., and Mishnaevsky, L.Jr., "Effect of Crack Orientation Statistics on Effective Stiffness of Mircocracked Solid," Int. J Solids and Structures, Vol. 46, No. 6, pp. 1574-1588, (2009)
Pindera, M.J., Khatam, H., Drago, A.S., and Bansal, Y., "Micromechanics of Spatially Uniform Heterogeneous Media: A Critical Review and Emerging Approaches," Composites Part B: Engineering, Vol. 40, Iss. 5, pp. 349-378, (2009)
Shen, H. and Brinson, L.C., "A Numerical Investigation of the Effect of Boundary Conditions and Representative Volume Element Size for Porous Titanium," J. Mechanics of Materials and Structures, Vol. 1, pp. 1179-1204, (2006)
Sangani, A.S. and Behl, S., "The Planar Singular Solutions of Stokes and Laplace Equations and Their Application to Transport Processes Near Porous Surfaces," Phys. Fluids A, Vol. 1, No. 1, pp. 21-37, (1989)
Torquato, S., Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Springer-Verlag, New York, (2002)
![]()

![]()