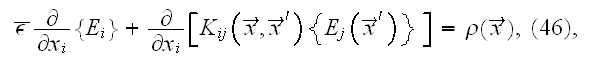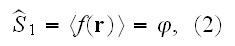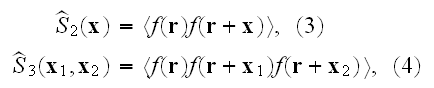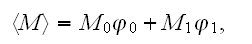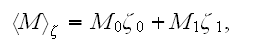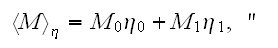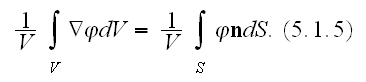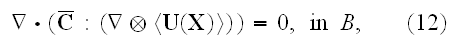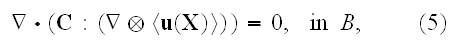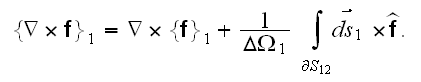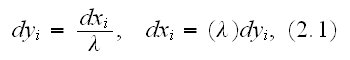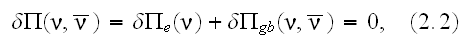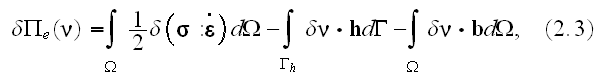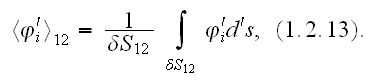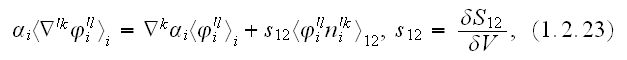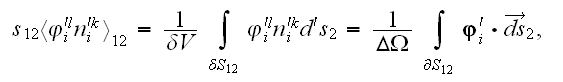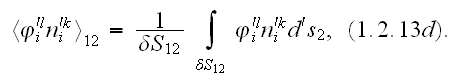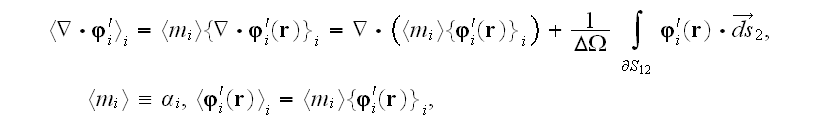What is in use in Continuum Mechanics of Heterogeneous Media as of Through
~1950 - 2005 ?
SECTION 1.4 ANALYSIS (LIMITED AND SELECTIVE) OF
"HETEROGENEOUS" THEORIES FOR HETEROGENEOUS MEDIA (MATERIALS) EXISTING UP TO
BEGINNING of THE XXI CENTURY IN CONTINUUM MECHANICS.
THAT IS UNBELIEVABLE, PEOPLE WANT TO DO THIS OBSOLETE
SCIENCE UP TO THEIR RETIREMENT?
To understand why the Homogeneous GO theorem based studies are insufficient,
softly said, or incorrect for the Heterogeneous media problems in Continuum
Mechanics we have to study laboriously few prominent, influential probably
studies of such kind. The other way around might give an impression that we
mostly bluntly criticize what was done by workers in this way of science making.
That is not our goal.
We have the sufficient place (and desire or possibility) here for considering
these studies thoroughly, because the nature of this way of doing science and
business in multiphase heterogeneous media Continuum Mechanics mainly in the
same mode of mathematical methodology as in other fields of physics representing
a treatment of Heterogeneous Media as a kind of Homogeneous ones, and that we
studied many years ago while publishing on the subjects as well as uploading and
saying on that in many parts of this website.
Meanwhile, because this field - the Continuum Mechanics is forming the base
for many sub-disciplines particular in Solid State mechanics, we ought to
discuss on few major developments as on examples of wrongdoing, of false
science, that strangling Continuum Mechanics for more than 40 years.
Keeping in mind what was said above in
Sections 1.1 - 1.3 we might now considering the tedious comparing and
analysis of those homogeneous GO studies using the point of view as
of the Heterogeneous WSAM theorem and of this kind other HSP-VAT
advancements, found throughout the last 40 something years.
If reader has enough qualifications and
patience to read this analysis up to the end, that is my goal
to help professionals and students to understand what's wrong in this field and
that the way out of this mess with CM actually was found in 90s
first through the WSAM rather theorems (HSP-VAT), and then the
Heterogeneous (Ht) Continuum Mechanics started sooner to stand
on its own. Right now we have done just few basic initial steps.
Meanwhile, don't get me wrong - I am not abolishing the
conventional Homogeneous one scale CM, I just saying that it is the part,
the inherent native part of the broader entity of Heterogeneous CM,
see our .
Say, nobody seems right now be so stupid saying that the Ht Thermal
Physics or Ht Fluid Mechanics are false subjects? Or somebody in the
traditional CM might dare to do this?
Also, there are no personal attacks on someone,
as I've heard in the past, read in our -
This is a healthy critique to force people stop doing silly
things and teach students wrong subject. I am not so naive to believe they
can do this for a moment. The publicity might get them stop doing this.
~~~~~~~~~~~~~~~~~~~~~~~~
Let's start with the good old publication incorrectly presenting the subject. There have being published hundreds like that.
Beran, M.J., "Application of Statistical Theories for the Determination of Thermal, Electrical, and Magnetic Properties of Heterogeneous Materials,"
in Mechanics of Composite Materials, Vol. 2, Ed. G.P. Sendeckyj, Academic Press, New York, pp. 209-249, (1974).
So, Why this the very good and general quality paper did not get much of
attention and the method either have not brought after more than 30 years much
of results ??
Beran (1974) stressed the attention (focused ) on the methods of statistical
treatment of elliptical second kind partial differential equations. That is
common base mathematics for homogeneous matters in many physical disciplines.
He discusses both an ensemble averaging as well as a volume averaging. Author
speaks on effective coefficients, also tells about the problem of the design
of composite materials with needed effective coefficients.
The basic starting field's distribution equation (3)
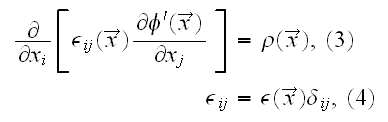
after averaging has the form
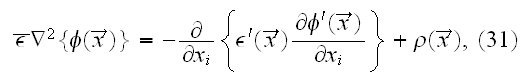
and we note that in this statistical averaging there is no techniques,
recognition of the specifics for the left hand side operator's averaging. No
difficulties with the GO theorem conditions fulfillment or about the WSAM
theorem application if any at all?
Also, we have to note here that in this kind of problem analysis and
evaluation, including a solution, no place is for material's consideration -
just a statistics, no place is for the phase (phases) description, no place for
interface description, and on the physics of interface elaboration. There are
the statistics of morphology and morphology parameters that are not directly
tied to the GE above.
That is out of consideration because there is no tools and power for doing
this in the statistical mechanics of one scale.
There is no talking about the first scale (there is no scale consideration at
all) physics and its mathematical representation.
Taking an ensemble average of equations is no problem at all in these types of statistical theory of heterogeneous materials.
1) The simple treatment of effective
coefficients problem is given in section V as for the
equation
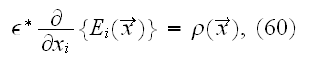
that is said needs to be compared to the original equation with the constant
coefficient
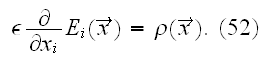
In this comparison, while actual substitution of one equation by another
there are so many issues mixed and out of description. Among them the vital one is
the issue of how to justify the connection of the one initial equation to the
effective coefficient equation?
Another natural question - Is this equation with effective coefficient correct? What kind
of fields (all of them) is used in these equations, etc.?
Regarding the very important issue of the effective coefficient bounds we
need to recognize that using the homogeneous concepts and theoretical
constructions we inevitably developing the same kind of useless characteristics
on bounds.
In section V we can find the text in p. 232: "This is so because as we know
from bounds we shall present below that it is impossible to specify 
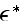 from just a knowledge of low-order statistical
information."
from just a knowledge of low-order statistical
information."
While this is the wrong statement generally, we would like to point out to
the tools of HSP-VAT.
The matter is that the techniques of HSP-VAT gives the ability to model,
simulate and make calculation practically of an exact nature, as long as we are
able to figure out the morphology features (that is now accepted as a solvable
task) and willing to invest into the much larger then the usual mathematical
physics project that is the two scale (at least) HSP-VAT mathematics simulation.
I would say - What is the point in finding the bounds of product 2x2 if then
saying whether it result will be more than 3 or/and less then 7, if someone can
calculate the exact value which is 4!? The similar story is with the bounds for
effective coefficients for heterogeneous media.
2) Thus, the substantial portion of section V
given to the detailed analysis of statistical theory using the three-point
correlation function for assesments of bounds for efective coefficients.
These issues have no sence to consider. Thou, efforts in finding the
effective coefficients (constants?) and their bounds by homogeneous tools for
heterogeneous materials used for more then 40 years by numerous researchers are
examples of waste of resources. The most valuable among them are the human
resources.
3) Section VI is devoted to experiment which
is meant to be in line with the assessment of the some three-point correlation
functions. All of this discussion on the issue of three-point correlation
function is actually based on and brought in life by Miller's (1969) "cell model
for real materials."?
This model is quite simplistic and is far beyond of correct construction for
averaging, averaged fields, and averaged equations.
4) In section VII on "Applications" done the
text that could be seen as the introductory text to a research on the purpose of
all these efforts in materials science, composites.
We can read in p. 243: "The principal application of statistical ideas to
problems of heterogeneous materials will probably be in the design of materials
with desired effective constants. The simplest way to illustrate this point is
to consider the design of a two-phase composite material that has a maximum
effective thermal conductivity.
For example, high thermal storage-low thermal conductivity materials are
sometimes seeded with high-conductivity inclusions to increase their effective
conductivity. Since the inclusion material is usually expensive relative to the
matrix material, it is important that inclusion shape and packing be optimally
chosen."
Also, in p. 244 we can read on the same: "Unfortunately, at this time, no one
has published specifications that will tell the engineer how to place and
size-distribute the inclusions in order to obtain the maximum value of 
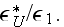 "
"
Since these 30+ years passed then anyone has heard of the solution of this
problem ?
Not at all. People even stopped to discuss and promise on this subject.
During the last 40 something years these kind of principal problems are not
solved. The reason is the same - for these two- and more scale multiphase
problems models used are insufficient in mathematical sence for claiming answers
to these questions on optimization.
See more explanation into our -
That is why the final section VII is full of incorrect concluding remarks and
wishes.
++++
5)For example, in the chapter by Beran (1974)
in pp. 239-242 given the solid piece on experimental (morphological mainly)
study done for the purpose of comparison the statistical theory based results on
effective constants in heterogeneous medium. A useless study because the theory
as it was asserted in 60-th - 70-th (and later on) is useless also.
6)
On the Dyson Equation said that:
Page 226 - "IV. Equations Governing the Mean Field
In section III, we pointed out that in order to determine 
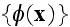 we must in principle solve an infinite hierarchy
of equations that contain all the statistical information on the
we must in principle solve an infinite hierarchy
of equations that contain all the statistical information on the 
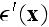 field."
field."
That's the BIG,BIG difference with the VAT procedures, where no infinite series of GE.
Page 226 - "In this section we wish to show that 
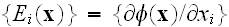 formaly satisfies an integro-differential equation
usually termed a Dyson equation. The kernel of the integral portion of the
equation is a function of all statistical information in the
formaly satisfies an integro-differential equation
usually termed a Dyson equation. The kernel of the integral portion of the
equation is a function of all statistical information in the 
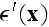 field. Since all the statistical information is
contained in a single kernel function, this equation may be used
phenomenologically in the absence of detailed information about the
field. Since all the statistical information is
contained in a single kernel function, this equation may be used
phenomenologically in the absence of detailed information about the 
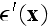 field.
field.
The character of the integrodifferential equation is quite different from
that of an ordinary differential equation, and we shall point out the need for
such an equation near rapidly varying source functions or boundaries."
While in the stochastic approach so nicely described in works like by Beran
(1974) one would note that this kind of approach has some features that we can
name as unacceptable, for example, such as:
st1) There is no volume of statistical
averaging, but either all the 3D cartesian (or in another geometry) coordinates
or the volume (body) of the problem. This assumption instantly brings the
question on correctness of the boundary conditions all-together with the
principal issue what kind of averaging theorem being applied - the homogeneous
GO theorem, or the heterogeneous WSAM kind of theorems (there are many of them).
st2) Further, the statistical averaging comes
with the necessity to consider "an infinite statistical hierarchy of equations"
(Beran, 1974; p. 222).
While we can read in p. 223 - "There is, however, no way in general to find a
finite set without some approximation."
That means - no dreams about the exact two scale, or even only an Upper scale
rigorous solution of heterogeneous problem! That is the disappointing
conclusion, isn't it ?
Meanwhile, with HSP-VAT tools we are able to solve either scale - an
Upper or Lower, or both scale problems.
st3) To solve the problem for averaged fields
in statistical averaging techniques (Beran, 1974) suggested the only way is by
using the integrodifferential equation of Dyson that is
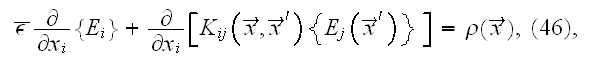
where 
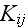 is represented by the infinite summation. We read
in p. 227: "equation (46) is an integrodifferential equation where the kernel
is represented by the infinite summation. We read
in p. 227: "equation (46) is an integrodifferential equation where the kernel

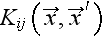 is given by an infinite number of
integrodifferential operators. In general
is given by an infinite number of
integrodifferential operators. In general 
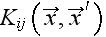 is very complex for arbitrary geometry even if Eq.
(47) " (with
is very complex for arbitrary geometry even if Eq.
(47) " (with 
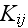 ) " is truncated at the first term."
) " is truncated at the first term."
We need to note here that this equation is all about the unkown field 
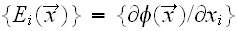 which is the gradient of our main sought field
which is the gradient of our main sought field

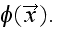 So, the problem is not solved yet in the case that
So, the problem is not solved yet in the case that

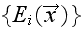 might be known.
might be known.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Brenner, H. and Adler, P.M., "Dispersion Resulting From
Flow Through Spatially Periodic
Porous Media. II. Surface and Intraparticle Transport," Phil.
Trans. R. Soc. Lond., Vol. A 307, pp. 149-200, (1982).
This is the useless large laborious study with the good topic and still
is useless. See what I had found as by their using of the GO theorem:
One can read in page 161 the shocking disclosure of their preemptive ignorence
on the control volume (REV) selection and on existing of other than GO theorems:
"Physically irrelevant mathematical questions of continuity may arise from
possible real physical discontinuities across 
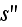 which is the interface surface (boundary between
the phases) "in the event that the unit cell faces
which is the interface surface (boundary between
the phases) "in the event that the unit cell faces 
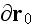 (bounding the unit cells
(bounding the unit cells 
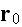 externally) coincide partly or wholly with the
phase boundaries
externally) coincide partly or wholly with the
phase boundaries 
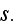 Such unnecessary mathematical complications can be
avoided by reverting to the artifice adopted in I of imagining
the unit cell faces to be drawn in such a way as to lie entirely within the
continuous phase. This choice of "curvilinear unit cell: insures complete
continuity of all functions across the cell faces
Such unnecessary mathematical complications can be
avoided by reverting to the artifice adopted in I of imagining
the unit cell faces to be drawn in such a way as to lie entirely within the
continuous phase. This choice of "curvilinear unit cell: insures complete
continuity of all functions across the cell faces 
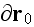 despite possible discontinuities across the phase
boundaries
despite possible discontinuities across the phase
boundaries 
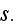 From the point of view of the physics, the
particular mathematical artifice adopted here is irrelevant since the unit cells
and their boundaries are but imaginary mathematical constructions, devoid of
physical reality."
From the point of view of the physics, the
particular mathematical artifice adopted here is irrelevant since the unit cells
and their boundaries are but imaginary mathematical constructions, devoid of
physical reality."
What forced these authors to write such an ignorent passage?
This particular
mathematical artifice is the one which allowed authors to draw
their incorrect studies, by the way.
Reading further we find that: "Indeed, ultimately we shall do away entirely
with the concept of unit cells and revert wholly to a scheme based upon the
introduction of spatially periodic functions satisfying boundary conditions only
on the phase boundaries 
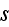 (see �6). In such a scheme the unit cell
boundaries play no role whatsoever."??
(see �6). In such a scheme the unit cell
boundaries play no role whatsoever."??
Which results down the road in page 163 in this formula of
such a "divergence" theorem - "The divergence theorem for any
tensor-valued field 
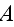 applied to the domain
applied to the domain 
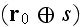 possesses the form"
possesses the form"
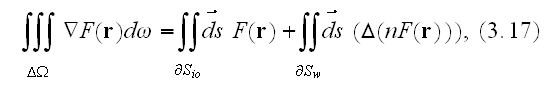
that is the homogeneous media GO theorem actually.
As the consequence of this derivation finally authors found the numerous
irrelevant formulae. For example, on the dispersivity dyadic for a Darcy flow in
porous media (5.4), (5.15) in pp. 170-171.
As of the most frivolous we can found the next one on the layered media
effective overall conductivity coefficients - (8.45)-(8.47) - "Equations (8.45)
- (8.47) apply for any one-dimensional spatially periodic conductivity field
D(z), continuous or discontinuous."?
We might conclude on this work that: Because the time of this
paper was 1980-82 that is many years after 60ths and 70ths paper publications on
basics of the VAT, then these authors would blame nobody but themselves that
their work (Brenner and Adler, 1982; Brenner, 1980) was
useless and incorrect.
Useless study -
INCORRECT - because used the GO theorem!
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Russel, W.B., Saville, D.A., and Schowalter, W.R., Colloidal Dispersions,
New York, Cambridge, Cambridge University Press, 1991.
This book came later then the one by Happel, J. and
Brenner, H., (1965, 1973), and the content is more advanced, still of not such a
tedious and calm story on the subject.
And I would say that the book came under the
editorship by Batchelor, G.K., and as such has a lot of references to his
works!!
The book has content which hide the more complicated sense of the field and
describe many things in a simplified manner.
For example, in pp. 35-37 given the text on assessment of stress and strain
in the REV, without the description of the REV and that alone makes possible to
write the formulae based on the GO theorem with no explanation of why is that?
In page 397 given the ensemble average velocities calculation based on the
following contemplation - "The integrals over the 
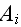 (that is the surface of particles - our notation)
account for interactions among particles within the representative volume, while
the integral over
(that is the surface of particles - our notation)
account for interactions among particles within the representative volume, while
the integral over 
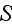 (this is the boundary surface of the REV- our
notation) represents the effect of particles outside. Strictly speaking,
(this is the boundary surface of the REV- our
notation) represents the effect of particles outside. Strictly speaking, 
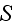 should deviate from the surface enclosing
should deviate from the surface enclosing 
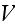 in order to bypass particles and remain in the
fluid."
in order to bypass particles and remain in the
fluid."
The same old story we have been pointing out so often while reading the
kind of the similar derivation in any physical field actually - it is about convenience
and safe way to say this while using the GO theorem. But it is grossly incorrect - see in
our pieces of text in
Reading further - "However, in the dilute limit
taking 
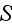 to coincide with the surface of
to coincide with the surface of

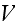 introduces an error of only
introduces an error of only 
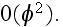 "
"
And where they took this estimation? This statement is untrue, because the
WSAM theorem should be applied in this case and this alone might give an error
even in hundred percent for estimation of average fields and their operators.
Going further we can read and find in the pages 493-497 in "Macroscopic
stresses" that formulae (14.10.2) and other in this subsection that relied
heavily upon the Homogeneous divergence theorem are incorrect and thou the
estimations are incorrect too.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Truesdell, C., A First Course in Rational Continuum
Mechanics, Baltimore, John Hopkins Univ., (1972).
Firstly I would like to say that this fundamental monograph probably will not
serving to students to the up high level as it is written with and was earlier
mentioned over in many publications.
The reason is the same as we argue here - because this is about physics,
mathematical physics, that means that author and other public interested in progress
in the field need from time to time ask themselves - Any communication to
reality we can observe or not? Any comparisons with the real world we have to do
or not now ?
The science of Continuum Mechanics that is the reflection of some concept that
the many fields in physics can be worked out with the single cartesian
coordinate system - No matter what!
So - how about an other or two of physically connected fields?
This book gives no answer to the question and would not, because it is about
one scale for all occasions. Even the most complicated physical phenomena
described with the mathematics of a one scale. Period.
There is no need in this book to talk on Heterogeneous media.
Theorem of divergence, of coarse Homogeneous GO, mentioned only in the mathematical supplement.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Berryman, J.G. "Variational Bounds on Elastic Constants
for the
Penetrable Sphere Model," J. Phys. D: Appl. Phys., Vol. 18, pp. 585-597,
(1985).
(This work done at Lawrence Livermore National Laboratory.
P.O. Box 808. L-200. Livermore, CA 94550).
(Sponsored by - under the auspices of the US DOE under
Contract W-7405-ENG-48 and supported specifically by the Base Technology Program
of the Earth Sciences Department.).
This is the example of the waste scientific product - and I use this one as
an example while analysing it for it's "scientific" value for the Milton numbers -
for spatial correlation functions?
In page 585 we can read: "Since Hashin and Shtrikman (1963) introduced their
variational principle for bounds on elastic constants of composites, many
improvements on these bounds have been found (Beran and Molyneux, 1966; Miller,
1969; McCoy, 1970; Silnutzer, 1972; Milton and Phan-Thien, 1982). The improved
variational bounds always require statistical and geometrical information about
the random composite - usually in the form of spatial correlation functions."
and further "... The penetrable sphere model is a hypothetical random
material composed of spherical particles randomly imbedded in a host material.
The locations of the sphere centres are uncorrelated in this model so the
particlas do overlap and the spatial correlation functions are relatively easy
to calculate. This model plays several important roles in developing the
theory......"
in page 586:
" The present discussion is limited to the three spatial correlation
functions measurable (Corson, 1974; Berryman, 1985) using photographs of
cross-sections of the material:
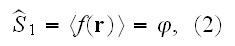
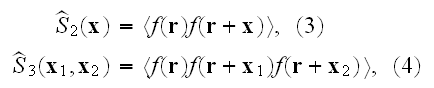
where the brackets indicate a volume average over the spatial coordinate

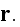 The volume fraction of constituent 1 is given by
The volume fraction of constituent 1 is given by

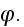 In writing equations (2) - (4), it has been
assumed that the composite medium is statistically homogeneous so that on the
average only the differences in the coordinate values are important."
In writing equations (2) - (4), it has been
assumed that the composite medium is statistically homogeneous so that on the
average only the differences in the coordinate values are important."
in page 589:
"...various formulas providing estimates of physical constants for composite
materials are known (Beran, 1968). Milton (1981, 1982) has recently shown how to
simplify the formulas of Beran and Molyneux (1966) and of McCoy (1970) by
introducing two parameters ( 
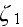 and
and 
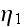 ) which depend on the microgeometry of the random
composite through the three-point correlation function
) which depend on the microgeometry of the random
composite through the three-point correlation function 
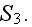 .."
.."
in page 590:
" Three averages of any modulus M can be defined according to
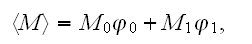
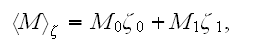
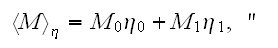
where 
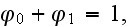 and
and 
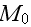 and
and 
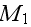 are the moduli value in corresponding phase 0 or
1. THAT'S JUST SIMPLE WAY TO FIND OUT THE EFFECTIVE COEFFICIENTS!!
are the moduli value in corresponding phase 0 or
1. THAT'S JUST SIMPLE WAY TO FIND OUT THE EFFECTIVE COEFFICIENTS!!
in page 596: "The main results of this paper are the values of the Milton
numbers for the penetrable sphere model which are presented in table 1 and
figure 2. These tabulated values may be used to provide estimates of elastic
constants in a wide variety of situations assumimg that materials of interest
have geometries which do not differ too much from that of the model. Until
spatial correlation functions of real material become readily available, this
model will provide a useful test case with narrower limits that those for the
Hashin-Shtrikman bounds. We would expect this model to be a reasonable
approximation to the geometry of a sintered powder or other synthetic materials
made by heating and/or pressing aggregates of particles to form a cohesive
solid."
Useless study: because that was done for
characteristics that are not shown in governing equations or parameters of
interest, but just declared as useful - these bounds of elastic moduli that are
not correct themselves. What for are these mathematical correlation dependences
estimated??
In more than twenty years since then I have not heard of implementation -
that might happen, that again being useful for scientific and technology points
of view.
All is this happen because authors of this direction (finding the bounds of elastic constants of composites) took the
modeling mode for their studies based on Homogeneous GO theorem, nothing less.
~~~~~~~~~~~~~~~~~~~~~~~
Happel, J. and Brenner, H., Low Reynolds
Number Hydrodynamics,
Sijthoff and Noordhoff, Alphen aan den Rijn, (1973).
We need to say more on this book - in terms of COLLECTIVE BEHAVIOR Problems.
In this book (we may say almost or classical good book) two last chapters -
8th and 9th are devoted to the matter of suspension moving in liquid while
considering mainly the very dilute and the more dense slow flow regimes.
The whole content of these two chapters are to make assessments of dynamics
of not a separate particle movement, but rather to describe and to find out the
parameters of the "clouds" of particles -actually averaged characteristics of
the Upper scale physics.
At the same time, there is no concepts or features (remind that was only the
60th and beginning of 70th) describing the second (Upper) scale field's
properties that are in fact sought in studies described and formulated in these
two chapters. These are averaged characteristics of bulk effects of the second
dispersive phase as, for example, nonlocal pressure drop 
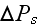 in liquid, differential volume element
in liquid, differential volume element 
 (as REV), permiability coefficient
(as REV), permiability coefficient 
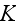 , filtration velocity
, filtration velocity 
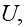 effective viscosity of suspension
effective viscosity of suspension 
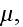 etc. etc.
etc. etc.
This the one scale handling of problems do not allow to obtain correct
analysis and mathematical formulae. For example, in chapter 9 we can find the
definition of effective viscosity of suspension in expressions (9.1.1), (9.1.2)
that are incorrect as soon as the boundaries should not be considered as
homogeneous surfaces, etc. etc.
We elaborated the two-scale theory for suspension flow in liquid and had
gotten the exact (or mathematically most strict) solution and simulations for
few such kind of problems with Kushch in 1994-1996. These advancements were not
published in open literature up to now, while we hope this take place in a
future.
Commonly, these two chapters in Happel and Brenner (1973) book give a
nice, broad analysis of single scale attempts to solve these broadly stated
Two-scale heterogeneous problems - the flow of suspensions, and the flow in
porous media. The chapters can be referred as for studying
what can not be done
with the one scale mathematical physics statement while the two scales are
natural for problems in this field.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Hashin, Z., Theory of Fiber Reinforced
Materials,
NASA CR-1974 Report, Univ. Pennsylvania, Philadelphia, pp. 1-690, (1972).
This is the useless 700 hundred report (monograph) because of the GO theorem used.
Will be commenting on the formulae and developments !
There were a lot of citations (references) in 80ths and 90ths (I remember
myself) to the publications authored and co-authored by Z.Hashin, for example,
see (1965a,b, 1970, 1972, 1983). In these studies dated back to the beginning of
60ths there were already proclaimed the theory which supposed to explaine almost
about everything in continuum mechanics of composites (Heterogeneous Media) -
elasticity, heat transport, electromagnetic fields basics, strength, etc.
The whole course of developments in these studies is based on artificially
(we explain why we use this word) simplified concepts and mathematics of bulk
averaging through the Volume - Surface GO theorem, and the Virtual Work Theorem.
Using the assigned one phase boundary REV see, for example Fig. 2.1.2 in 1972
report for NASA by Hashin (1972) -
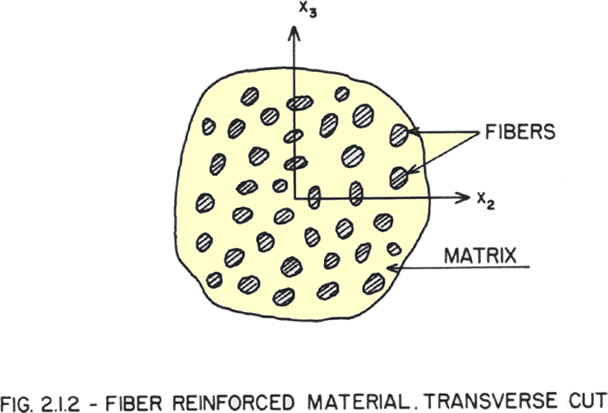
which explains why much of the formulae in this report, for example, like
(5.3.5), (5.3.21) that are the key formulae among others, are illustrations of
erroneous mathematics.
On page 1 we read: "From the engineering point of view the most important
type of composites at the present time are Fiber Reinforced Materials (...FRM)."
On page 3: " it is an attempt to present a theory of FRM which is reasonably
rigorous and is at the same time oriented towards the engineering uses of such
materials."
In page 534 -
The average of gradient of field is given as "the gradient theorem" in the
homogeneous interpretation
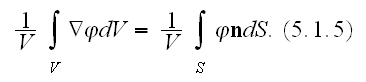
We can read in the same page; "The proof is immediate: The volume integral in
(5.1.3) is converted to two phase region surface integrals by means of the
divergence theorem. The surface integrals on the interface cancel because of
(5.1.1c) and the reversal of the interface normal. Then (5.1.5) follows at
once."
While this is INCORRECT for Heterogeneous Materials.
Now it is the good time of questioning - And where are these materials, texts,
research, promises, design
hopes and models with their embodiments based on this and like this theories now
? After 30-40 like years period of utilization where are the proofs of their
usefulness ? Or correctness?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Hori, M. and Nemat-Nasser, S., "On Two Micromechanics
Theories
for Determining Micro--Macro Relations in Heterogeneous Solids," Mech. Materials, Vol.31, Issue 10, pp. 667-682, (1999).
Abstract
The average-field theory and the homogenization theory are briefly reviewed
and compared. These theories are often used to determine the effective moduli of
heterogeneous materials from their microscopic structure in such a manner that
boundary-value problems for the macroscopic response can be formulated. While
these two theories are based on different modeling concepts, it is shown that
they can yield essentially the same effective moduli and boundary-value
problems. A hybrid micromechanics theory is proposed in view of this
correspondence. This theory leads to a more accurate computation of the
effective moduli, and applies to a broader class of microstructural models.
Hence, the resulting macroscopic boundary-value problem gives better estimates
of the macroscopic response of the material. In particular, the hybrid theory
can account for the effects of the macrostrain gradient on the macrostress in a
natural manner.
Author Keywords: Micromechanics; Homogenization; Average field theory;
Multi-scale anisotropy
Corresponding author. Tel.:+1-619-534-4772; fax:+1-619-534-2727; e-mail:
sia@halebopp.ucsd.edu
.......................
Here we need to make a dear note that neither any of authors mentioned in
the work as Hill (1963), Mura (1987), nor authors themselves are experts or
really made a direction in a correct "average-field" theory.
To our delight and experience we observed and discussed few years earlier
(seems in 2003-2004) with one of the authors (Nemat-Nasser) the work itself and
outcome produced in this publication.
Authors writing deserves to be commented here for clarity of agruments. As to
the statement, for example, in page 667 where one can read that: "Average-field theory. This theory is based on the fact that the
effective mechanical properties measured in experiments are relations between
the volume average of the strain and stress of microscopically heterogeneous
samples. Hence, macrofields are defined as the volume averages of the
corresponding microfields, and the effective properties are determined as
relations between the averaged microfields."
This definition is incorrect and incomplete. We would not be surprised that
using this definition authors came to their conclusions.
What is incorrect regarding this statement:
a) "effective
mechanical properties measured in experiments are relations between the volume
average of the strain and stress of microscopically heterogeneous samples," -
these properties are the result of experimental set-up made for Homogeneous
medium, and as such bearing the features of GO homogeneous medium theorem based
experimental set-up. Not a Heterogeneous Medium Experiment (HtME) on Elasticity
properties. This is the experiment (HtME) where the dependency of stress on a
displacement field as of an averaged field usually established, thus this
dependency would consist also within the HtME provided with the surficial
integrals for the displacement fields over the interfaces within the measured
volume, within the REV or one of possible REVs taken as for this curtain
experiment. So, This should not be the Homogeneous experiment, if we are
determined to deal with the our Heterogeneous medium. Well, in this case we have
to obtain the the Heterogeneous dependence between the average displacements and
average stress in the whole Heterogeneous medium, in the separate phase(s) of
the medium.
b) The Upper scale elasticity model fields are determined throughout not
only the Lower scale microelasticity fields, but also and that is the major
constitutive part of Upper scale physics, by the Upper scale Ht Governing
equations solution for the problem's domain Heterogeneous medium. Otherwise, if
the Upper scale GE would be accepted as of Homogeneous medium, then the Upper
scale Effective Coefficients (EC) and Boundary Conditions (BC) would not the
conventional Homogeneous medium EC and BC.
c) In many, most probably, situations the Upper scale statement conditions
are of the prevailing importance for the Heterogeneous problem (elasticity in
this case) and as such the Upper scale mathematical statement must be stated
rigorously, as much strict as the theory allows. That means - the Lower and the
Upper scale GEs must be constructed so directly mathematically tied, as they are in
physical nature of the problem, usually. That means also - that the Top-Down as
well as the Bottom-Up sequances should be used for mathematical formulation of the
Two Scale Problem. Also, the Upper scale GEs formulated as the conventional
homogeneous statement are incorrect if taken separately from the correct Lower
and Upper scale Heterogeneous GEs as in this paper, for example.
In this paper we would find the incorrect Upper scale averaged governing
equation for the displacement field 
 , Eq. (12) in page 670
, Eq. (12) in page 670
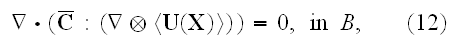
which was obtained, and authors do stress out on that, with help of using the
GO theorem.
By the way, in this equation the average displacement field 
 is the field averaged over the entire elastic body
is the field averaged over the entire elastic body

 !?
!?
So, in this way there will be no solution, properties and analysis of phase
distinguished fields can be done. No interaction between phase depending
properties, etc., etc. ? Strange development.
This governing equation (12) for supposed to be the averaged field 
 is of the same look and actually exactly the same
as the governing elasticity equation (5) in page 669, for homogeneous elastic
body as we know it
is of the same look and actually exactly the same
as the governing elasticity equation (5) in page 669, for homogeneous elastic
body as we know it
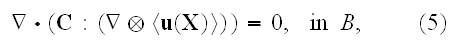
The main conclusion of the study in the page 680 is
that:
"It is shown that the two micromechanics theories, the average-field theory
and the homogenization theory, can be related to each other, even though they
are based on different concepts. In particular, the first order terms in the
expanded strain and stress fields of the homogenization theory correspond to the
average-field theory."
We can remark on that - this
is obtained because the initial statements for the so-called "average-field
theory" were incorrect, following from this the final output conclusion stated
in the paper is incorrect also.
There is no one published source of information on true averaged scaled
physical fields theory (VAT, HSP-VAT) referred in this paper and in the book by
the same authors. Referred works by Beran, Hashin and others are the incorrect
ones in terms of averaging statements and mathematics.
Nevertheless, we can draw the one at least useful conclusion regarding this
work study which is - This study is a unique probably example of comparison
(incorrect anyway) of averaging (incorrect) GE and of the homogenization GE for
the same physical task. The results authors obtaine are incorrect in terms of
comparison - and this gives us the GOOD EXAMPLE of DIFFERENCE between the averaged
correctly (HSP-VAT so far is the only way) elasticity in heterogeneous medium statement and of the Homogenization theory.
The other examples given in the Homogenization theory are actually comparisons of
the single scale different notation expanded and of the initial GE and have no
interest for Multiscale development.
Further, we can observe in the Fig. 2 (paper's page 669)
that the boundary surfaces for the REV are placed within the single phase. Of
course, this is incorrect. One can guess, that the deposition of second and more
phases, defects, etc. within the embracing matrix is taken for purpose, see our
analysis on this artificial arrangement in -
In the introduction in page 667 we can read that: "One major objective of
micromechanics of heterogeneous materials is to determine the effective overall
properties by certain microscopic considerations. The effective properties are
then used to evaluate the response of structural elements which consist of
heterogeneous materials. Consider two basic approaches for obtaining the overall
response of a heterogeneous medium: (1) the average-field
theory (or the mean-field theory) and (2) the
homogenization theory. Roughly speaking, these are physics- and mathematics -
based theories, respectively. Here, the basic characters of these two theories
are interpreted as follows: "
"...Homogenization theory. This theory establishes
mathematical relations between the microfields and the macrofields, using a
multi-scale perturbation method. The effective properties then naturally emerge
as consequences of these relations, without depending on specific physical
measurements."
" In this paper, we are primarily concerned with establishing a link between
the average-field theory and the homogenization theory, clarifying their
similarities and differences."
++
In the Page 674 authors say: "There are, however, two major differences
between these two theories. The first difference is the modeling of the
microstructure: the homogenizatio theory uses a unit cell of the periodic
structure, while the average-field theory considers a representative volume
element of a statistically homogeneous body.
The second difference is that the homogenization theory is able to treat the
macro-micro relations more regorously, allowing higher-order terms in the
singular perturbation expansion."
Both statements are wrong -
in the HSP-VAT one not
necessarily uses the "statistically homogeneous body" and this is the great
advantage (we spoke few times on that); the HSP-VAT just gives with the proper
mathematical statement the Exact Solution on both Scales that is opposite to the
Homogenization theory always approximate solutions for the Lower scale.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Nemat-Nasser, S. and Hori, M., Micromechanics: Overall Properties of
Heterogeneous Materials, 2nd edition, Elsevier Science
B.V., Amsterdam, (1999). 786 p.
.....................
In this fundamental book given the parts related to averaging procedures,
theorems, etc. all aplied toward the Elasticity theory for Heterogeneous
materials. But the basics for averaging made of conventional Ostrogradsky-Gauss
theorem, not heterogeneous theorems by WSAM
(Whitaker-Slattery-Anderson-Marle ), see, for example, pp.59-60.
Page 11 we see the determination of the REV (RVE in notation by authors) -
"An RVE for a material point of a continuum mass is a material volume which is
statistically representative of the infinitesimal material neighborhood of that
material point. The continuum material point is called a macro-element. The
corresponding microconstituents of the RVE are called the micro-elements. An RVE
must include a very large number of micro-elements, and be statistically
representative of the local continuum properties."
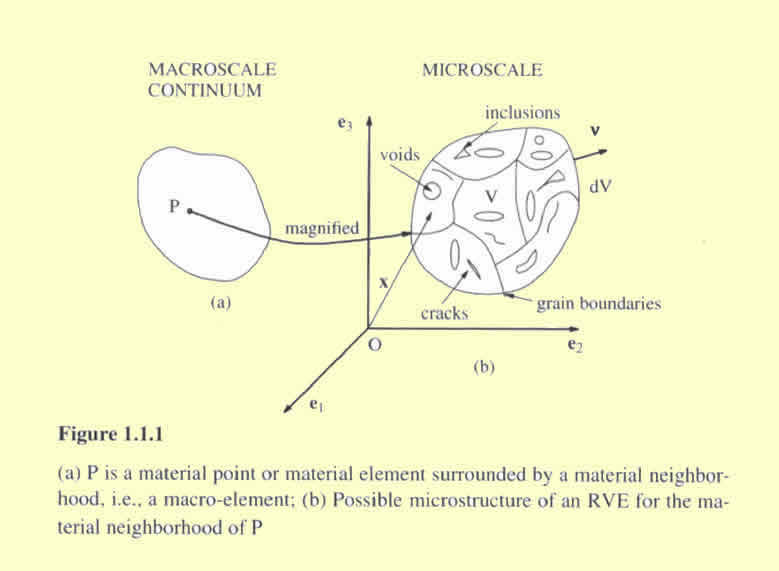
This is only the part of the normal definition of the REV, but in its part it
is O.K.
The missed points are the descriptions and properties of the two scales and
how the REV and the Lower scale medium are corresponding one to another?
For What reason we consider the REV ? For the macro-element, point of the
Upper scale, and what more for?
Page 44 gives the unjustifiable communication of the Boundary Conditions on
the boundary of REV ?? to the conventional BC as "The RVE is regarded
asstatistically representative of the macroresponse of the continuum material
neighborhood, if and only if any arbitrary constant macrostress 
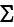 produces through (2.5.26a) a macrostrain
produces through (2.5.26a) a macrostrain 
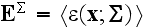 such that when the displacement boundary
conditions (2.5.27a) are imposed instead, then the macrostress,
such that when the displacement boundary
conditions (2.5.27a) are imposed instead, then the macrostress, 
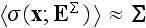 , is obtained, where the equality is to hold to a
given degree of accuracy."
, is obtained, where the equality is to hold to a
given degree of accuracy."
To this point we must ask -
What are the BC on the boundary of REV ? For what aim? Is this the problem's
domain as a whole ? Seems authors of the book considering this option.
The excerpt in the page 471 shows explicitly that authors bearing in mind the
averaging procedures in the book as for and the one scale methodology. We read -
"The second important difference between the concept of an RVE and the periodic
model is that, through the application of a Fourier series representation, the
periodic (elasticity) model can be solved essentially exactly in many important
cases, whereas in the case of a RVE, only estimates based on specialized models
(e.g., the dilute distribution, the self-consistent, and the differential
models) are possible."
Which is stated as such because authors do not believe as for existance of
the second scale physics and mathematics, although, this statement is also
incorrect, as soon as there are the Upper scale problems solved for many
instances. The most clear, simple, and straightforward of them can be seen in
our texts even and mostly here in the website.
We have shown in many places of this website,
by means of the Two scale solutions, especially with the exact Two scale solutions of
those few common textbooks known problems, see in -
that this new kind of Mathematical Physics old problems can be successfully tackled and solved either.
While also obtained after 2002 the analytical (and numerical) solutions of the following classical problems
that have not been solved for many decades by other methods
(given in textbooks the Lower Homogeneous scale "solutions" are wrongly attributed
to the Upper Heterogeneous scale averaged fields)
These solutions leave no chances for calculations or comparison with experiment
of the Upper scale characteristics using the basis of Homogeneous GO. This has no sense, invalid for Heterogeneous problems.
+++
These two notions below have the common ground applicable and to this book,
that say that the physics of heterogeneous (composite) materials should comply
with:
A) The physics of each separately taken smallest distinguashable Homogeneous
part (grain, crystalline, bead, etc. ) of material. Most often this is the piece
of a separate phase in a multiphase material.
B) The physics of overall properties of the material as the whole Upper scale
body (the whole volume of given composite material), or as of a substantial part
of it containing within itself the infinite number of REVs.
One of the ground concepts in the book by Nemat-Nasser and Hori (1999) is
that the averaging is done over the REV with the applied boundary conditions to
the REV's boundary? One needs to ask then - Either this is the whole problem's
volume or there is not a REV averaging that supposed to be used in the
"averaging" procedure. All this is done probably to prevent connection of
neighboring REVs and finding the correct Upper scale governing equations (GE)?
We can read with amazement, see p. 38, that - "It is seen that the
discontinuity in the field quantities does not influence the average stress,
strain, strain rate, and the rate of stress-work, if the tractions, the
displacements, and the velocity fields are continuous in V."?
Obviously, just observing the Fig. 2.4.1 given in page 36
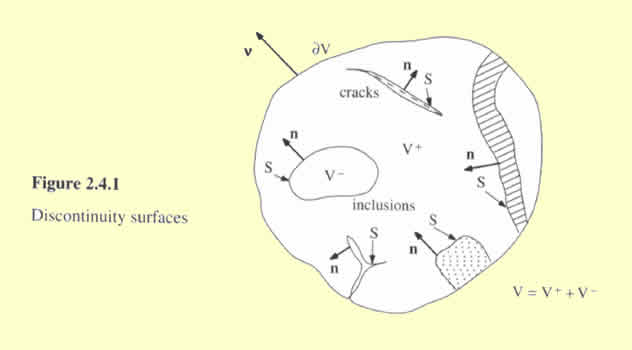
which embraces more than 3 phases of the 3D nature and the cracks within the
REV which can be considered as 2D phases it's hard to accept the homogeneous
concept of elasticity for heterogeneous materials being developed by authors.
That is, the mathematics and physics of multiphase media arrived at in the
Chapter 1, Section 2 are all wrong as long as the whole deductions were achieved
throughout the use of Homogeneous Gauss-Ostrogradsky theorem
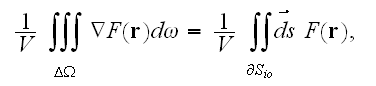
where 
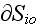 is the input-output surface surrounding the volume
is the input-output surface surrounding the volume

 .
.
For a Heterogeneous medium! That all means no distinguishing of the one phase
from other phases in a 3D (and 2D, 1D) cases, by taking into account interplay
between the phase's related phenomena, etc. etc.
Actually, in this way the body of solid state mechanics elasticity theory,
plasticity theory and related areas being treated as the ordinary Homogeneous
media theory, the one is known to professionals and published intensively about.
These mathematical models and treatments do not allow to get even correct
results, not saying about searching for the properties related effects, see in
our -
It is of general surprise that even the products of physical fields declared
as the linear systems?! And averaged products macrofields are linear - pp. 65-66 also?.
The content of the book done in the fashion just mimicking (imitating) the
theory, description, modeling and simulation of the solid state heterogeneous
media, composites mechanics as in the areas of elasticity theory, plasticity
and, of coarse, the strength mechanics. Serving for the false hope and effort to
reach the truth.
+++++
The second failure after using the GO theorem for heterogeneous media as for
homogeneous ones in continuum mechanics(in almost 100% of books) is the
acceptance and even sometimes "proves"(?) that the averaged product of fields is
equal to the product of averaged fields!?
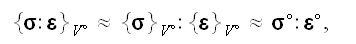
We can read in p.54 (Nemat-Nasser and Hori, 1999) - "Thus, averages taken
over any RVE in B
 are essentially the same as those taken over B
when the RVE is suitably large. For statistically homogeneous B, it therefore
follows that
are essentially the same as those taken over B
when the RVE is suitably large. For statistically homogeneous B, it therefore
follows that
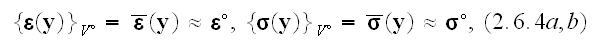
where 
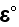 and
and 
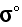 are the prescribed uniform farfield strains and
stresses."
are the prescribed uniform farfield strains and
stresses."
This is the false statement.
This expression assumption allows authors to do in many important issues
unbelievable simplifications and stretching.
For example, in pp. 54-57 (Nemat-Nasser and Hori, 1999) we can read the
reasonings ("proves") that the operation of differentiation commutes with the
operation of local averaging!
So, there is no need to incorporate the WSAM theorem for heterogeneous media
!!!
++
An Extract taken from the HSP-VAT course on "Heterogeneous
Electrodynamics ...":
''In accordance with one of the major averaging theorem - theorem of
averaging 
 operator, the WSAM theorem (after
Whitaker-Slattery-Anderson-Marle) the averaged operator
operator, the WSAM theorem (after
Whitaker-Slattery-Anderson-Marle) the averaged operator 
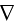 becomes
becomes
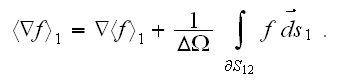
Meanwhile, the foundation for averaging made, for example, by Nemat-Nasser
and Hori (1999) (and many others) is based on conventional homogeneous
Gauss-Ostrogradsky theorem (see pp.59-60), not of its heterogeneous version as
the WSAM theorem.
The differentiation theorem for intraphase averaged function is
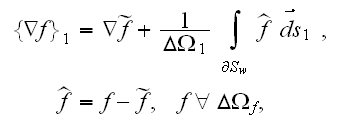
where 
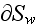 is the inner surface in the REV,
is the inner surface in the REV, 
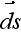 is the second-phase, inward-directed differential
area in the REV (
is the second-phase, inward-directed differential
area in the REV ( 
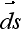 =
= 
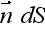 ).
).
The same kind of operator involving 
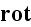 will result in the following averaging theorem
will result in the following averaging theorem
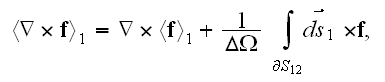
also as its consequence the another theorem for intraphase average of 
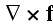 is
is
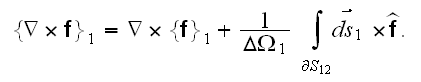
~~~~~~~~~~~~~~~~~~~~~~~~
Chen, J.-S. and Mehraeen, S., "Multi-scale modelling of
heterogeneous materials with fixed and evolving microstructures,"
Modelling Simul. Mater. Sci. Eng., Vol. 13, pp.
95--121, (2005).
MODELLING AND SIMULATION IN MATERIALS SCIENCE AND ENGINEERING;
Jiun-Shyan Chen and Shafigh Mehraeen, Modelling Simul. Mater. Sci. Eng., 13
(2005) pp. 95--121.
This is the rather thick paper with the claim for Multiscale formulation of
the Heterogeneous problem. While the Fig. 10 (p. 106) depicts the desire to
describe the two scale solid state mechanics Problem for elasticity, in reality
it is the single physical scale Homogeneous description of state using
homogenization solution method.
This is not a Multiscale Modeling - this is the Homogenization modeling using
the special method of multigrid numerical Galerkin method.
Still, this paper and the paper below might be serving as examples of an attempt
to develop the moving intergrain boundaries in composites.
~~~~~~~~~~~~~~~~~~~~~
Chen, J.-S. and Mehraeen, S., "Variationally Consistent
Multi-Scale Modeling and Homogenization of Stressed Grain Growth," Comput. Methods Appl. Mech. Engrg., Vol. 193, pp. 1825-1848,
(2004).
This is one of numerous claims for multiscale modeling of physical phenomena,
in this case using the asymptotic expansion of field variables with the
following development of "multi-scale" Euler governing equations along. We will
follow the main arguments and concepts referred in this paper in the effort (the
next one following many previous) to address the "Multi-scale" treatment issues
raised in this paper.
In the Introduction to the paper given a nice review of studies related to
"multiscaling" in continuum mechanics. We can read in p. 1826:
"Quasicontinuum method [12,22,23] has been proposed for problems requiring
the simultaneous resolution of continuum and atomistic length scales in a
unified manner. In this approach, the continuum part is furnished by finite
element method where mesh adaptivity is employed to provide multi-scale analysis
capabilities near lattice and other highly energetic regions, and proper weight
distribution is introduced for handshaking regions. A bridging scale scheme has
been proposed to separate basis functions of 2 scales in the handshaking region
[26]. Based on the bridging scale technique and projection of the MD solution
onto the coarse scale shape functions, a coupling of molecular dynamics and
continuum mechanics simulations has been proposed [16, 27]. In the context of
multi-scale methods, a multi-resolution analysis by utilizing wavelet-like
functions in the framework of meshfree method has also been introduced to
construct hierarchical coarse-fine decomposition [14,15,30]. "
The main objection to this kind and to the one specific statement above in the referred paper by Chen and Mehraeen (2004), is that in these simulation techniques they
can not describe properly the - "coupling," "multiscaling," "connection of
scales," "scale bridging," etc., because they can not properly address and
formalize the collective behavior, collective physical subjects phenomena at the
neighboring physical scales as well as the surficial phenomena all the said
simultaneously in Modeling Governing Equations.
That is because they use for GE developing the Homogeneous GO
theorem! That's simple.
These are really the MULTI-RESOLUTION methods those using sometimes
the different scales to solve the INCORRECT problem's statement.
Why it is incorrect - BECAUSE FOR MULTISCALE PROBLEM
INSTEAD OF MULTISCALE PHYSICAL STATEMENT FORMULATED AS THE MULTISCALE
MATHEMATICAL STATEMENT BEING USED AND "SOLVED" THE SINGLE SCALE PHYSICAL AND
MATHEMATICAL PROBLEM USING the MULTIRESOLUTION STATEMENTS!
HAVING NO DIFFERENT SPACES - JUST SINGLE SPACE FOR
ANY PHYSICAL PHENOMENA!
WHERE the DOT for every resolution statement IS THE
POINT with no physical subject, physical meaning inside, just the value of the
field at this dot.
AND EVERYTHING BEING ADJUSTED TO THE ONE SCALE EXPERIMENTAL
DATA (for any scale experiment) USING THE "COEFFICIENTS", the magic property of
coefficients. After all, these coefficients are also of the single scale
Homogeneous matter.
Let's follow the formulae in page 1827 where we can read on
the basics of approach:
"The multi-scale hierarchy from a macro-scale continuum to a meso-scale
network of polycrystalline material under consideration is shown in Fig. 1.
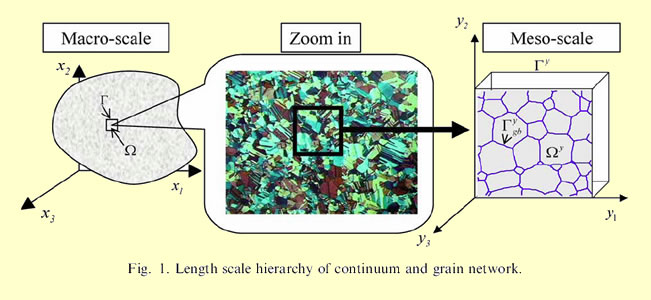
Let x-coordinate be the macro-scale coordinate system in the physical domain.
A unit cell with domain 
 and boundary
and boundary 
 of a continuum in the physical domain is mapped to
referential domain
of a continuum in the physical domain is mapped to
referential domain 
 and boundary
and boundary 
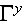 measured by a meso-scale y-coordinate. The macro-
and meso-scale coordinate are related through a scaling parameter
measured by a meso-scale y-coordinate. The macro-
and meso-scale coordinate are related through a scaling parameter 
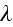 by
by
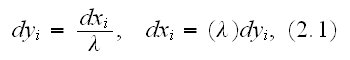
where 
 is a very small
real number. Thus a given length measured in the
y-coordinate is scaled by a factor
is a very small
real number. Thus a given length measured in the
y-coordinate is scaled by a factor 
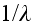 by its true scale measured in the x-coordinate."
by its true scale measured in the x-coordinate."
This means and authors write straight about that -
the scale in y-coordinate is not a physical scale, it is the
mathematical convenience, the mathematical habitat trick for convenience of the
finding the solution. We are not looking into some physical sense while
selecting this or numerous other kind of coordinate resolution.
Going further in p. 1827 we read:
"Consider a unit cell in the physical domail subjected to a surface traction

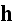 on boundary
on boundary 
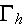 as shown in Fig. 2.
as shown in Fig. 2.
Fig. 2.
The grain boundaries in the unit cell are denoted as 
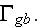 A variational equation for stresses grain growth
based on the principle of virtual power described in the x-coordinate [4] is as
follows:
A variational equation for stresses grain growth
based on the principle of virtual power described in the x-coordinate [4] is as
follows:
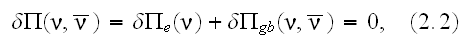
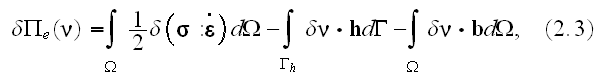
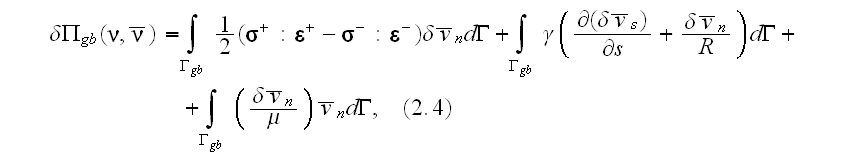
where 
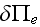 is the virtual power associated with deformation,
is the virtual power associated with deformation,

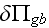 is the virtual power associated with driving
forces acting on grain boundaries,
is the virtual power associated with driving
forces acting on grain boundaries, 
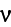 is the grain material velocity,
is the grain material velocity, 
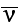 is the grain boundary migration velocity,
is the grain boundary migration velocity, 
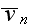 is th enormal velocity pointing away from the
center of curvature of the grain boundary,
is th enormal velocity pointing away from the
center of curvature of the grain boundary, 
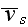 is the tangential velocity along the grain
boundary,
is the tangential velocity along the grain
boundary, 
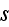 is the coordinate along the grain boundary,
is the coordinate along the grain boundary, 
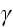 is the surface tension (the boundary energy per
unit area),
is the surface tension (the boundary energy per
unit area), 
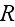 is the radius of curvature of the grain boundary,
is the radius of curvature of the grain boundary,

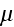 is the mobility representing the ease with which
the grain boundary can migrate,
is the mobility representing the ease with which
the grain boundary can migrate, 
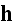 is the surface traction applied on the traction
boundary
is the surface traction applied on the traction
boundary 
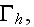

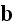 is the body force,
is the body force, 
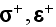 are the stress and strain in the grain that gains
virtual area
are the stress and strain in the grain that gains
virtual area 
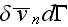 (grain A), respectively, and
(grain A), respectively, and 
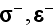 are the stress and strain in the grain located on
the other side of the boundary (grain B), respectively, as shown in Fig. 3. The
detail discussions can be found in [4]. We assume the stress-strain relation
follows an anisotropic creep law:
are the stress and strain in the grain located on
the other side of the boundary (grain B), respectively, as shown in Fig. 3. The
detail discussions can be found in [4]. We assume the stress-strain relation
follows an anisotropic creep law:
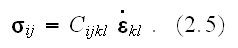
To describe the multi-scale material behavior, the material velocity 
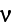 is expressed in the following asymptotic expansion
form
is expressed in the following asymptotic expansion
form
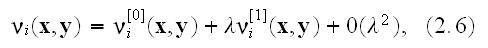
where 
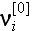 and
and 
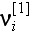 are macro (coarse)-scale and meso (fine)-scale
components of material velocity, respectively, and the superscript
are macro (coarse)-scale and meso (fine)-scale
components of material velocity, respectively, and the superscript 
![$[n]$](whatsup_files/HomogAnalContMech__122.gif) denotes the level of scale.
denotes the level of scale.
For a function expressed in both coarse and fine scale coordinates, the
following relationship can be obtained,
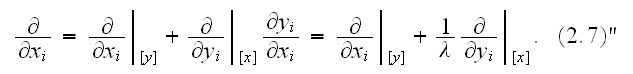
In the above excerpt the biggest doubts are toward the
expressions for a virtual power (2.3), (2.4) - those are just homogeneous
decriptions of the possibilities at, along and with the grain boundary surface

 and, of coarse, the averaging concerning formulae
for averaging of differential operators over the domain
and, of coarse, the averaging concerning formulae
for averaging of differential operators over the domain 
 .
.
These all expressions (2.2) - (2.4) for virtual powers separate grain growth
might be seen as useless ones when the real scaled consideration applied.
For example, when the elasticity laws being aplied at the scale of domain

 (of a separate grain fine scale), and for the
Upper scale of domain
(of a separate grain fine scale), and for the
Upper scale of domain 
 which is based on the x-coordinate system. This
analysis on the averaging of the elasiticity homogeneous dependenceies we have
made back in the 90s.
which is based on the x-coordinate system. This
analysis on the averaging of the elasiticity homogeneous dependenceies we have
made back in the 90s.
Also importantly to say this for students, that the relationship shown in the
page 1828 - (2.7) that tying up the partial derivatives for two system
coordinates is actually incorrect in n-coordinate systems, 
 That is, remember, that they need this
transform while applying to parts of the differential
operators. This kind of errors often workers in Fluid Mechanics - Turbulence
specifically, did in the past while doing deduction course.
That is, remember, that they need this
transform while applying to parts of the differential
operators. This kind of errors often workers in Fluid Mechanics - Turbulence
specifically, did in the past while doing deduction course.
This is the transformation that quite often used in the past and is
incorrecly used for the conservation equations.
Summarizing the outlook for this excerpts in pp. 1827-1828, we can say that
this kind of methodology, expressed in this work of 2004 and other works of
given authors group (2005, etc.), presents itself as the homogenization
procedures aimed to deal with the complicated heterogeneous media solid state
mechanics problem.
But this is not even a two-scale method. Not a "multi-scale" physics
treatment as authors want to position this work at.
No interscale dependencies were property set-up and determined in terms of
Lower Scale Domain Upper Scale Point, etc. as can be expected from Fig. 1 (page 1827).
So, this is the mathematical methodology (no good physical grounds)
attempting to develop and claim more than the one scale used in the solution
procedure. Anyway, it is not a physical and mathematically formulated two- or more
physical scale methodology.
Following this, we can also say that the developed grain topology
transformation equations including the grain boundaries evolution equations were
developed incorrectly.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Mehraeen, S. and Chen, J.-S., "Wavelet-Based Multi-Scale
Projection Method in Homogenization of Heterogeneous Media,"
Finite Elements in Analysis and Design, Vol. 40, pp.
1665-1679, (2004).
We need to talk here about their better Homogenization technique and about the
"mirror technique" at the boundaries.
Abstract: "Standard homogenization of highly heterogeneous
media often filters out the fine
scale information, and as a consequence, it produces acceptable results only
for certain type of periodic structures. In this work, a wavelet-besed
multi-scale homogenization is introduced for highly heterogeneous
materials where the standard asymptotic technique cannot be effectively
applied.
A set of scaling and wavelet functions based on the linear hat function and
its corresponding wavelet transformation matrix are constructed. The advantage
of this wavelet transformation constructed by hat function compared to that
using Haar function are identified. The mirror image technique has been employed
to preserve the accurate representation of boundary conditions and to avoid
numerical oscillation near the boundaries. This wavelet-based multi-scale
transformation hierarchy filters out the high-scale components of the solution,
and thus provides an effective framework for the multi-scale selection of the
most essential scales of the solution."
So, they talk themselves about the single, the one solution -single scale.
The problem with these NUMEROUS DRUM-NOISING texts and publications with
constant reminding of the words "multiscale," "hierarchy," in connection to
words "heterogeneous," "media," "materials," "scaling," as in works by these
authors and by Oden et al. (1999), Fish and Belsky (1995), among many.
These words beat out of unexperienced reader the thought,
the mean, that these are the really "Multiscale physical problems and their
solutions".
And this is dangerous profanity of the mean of physical
multiscaling!!
The physical multiscaling has become mixed, substituted by just old known
tool of mathematical multiscaling, but the worst thing is that the authors of
these works often keep thinking and representing their works as about the
Physical Multiscaling !
In page 1666 they write:
"The first method is homogenized Dirichlet projection method which was
developed based on the concept of hierarchical modeling (outlined by
us). In this method, the mathematical model at the coarsest level is represented
by homogenized material properties. This is referred to as the homogenized
problem, and the exclusion of heterogeneity generally makes the homogenized
problem computationally inexpensive compared to models of finer scale. Using a
posteriori modeling error, the accuracy of the solution capable of representing
the homogenized behavior of the original heterogeneous problem is estimated. In
regions where the modeling error exceeds a preset tolerance, a finer scale model
is used and a correction to the homogenized solution is made. This
homogenization procedure is continued until the error tolerance is met [2]."
In this kind of "
RAVING
" "hierarchical modeling"
sorry for the word, but people do not study anything but their own backyard only, the main error is that the coarsest level scale mathematical model is represented as
the unreal homogeneous statement GE with the incorrect Upper scale effective
coefficients!!!
This is the grave mistake of Homogenization theory - pretending for
the two physical scales description.
Here again is used the MULTIRESOLUTION (Multigrid) method -
because as for the Multiscale problem instead of Multiscale physical
statement formulated as the Multiscale Mathematical statement is being
used and "solved" the single scale physical and mathematical problem
using the MULTIRESOLUTION or Multigrid (as it used sometimes) statements!
Among references can be found:
[2] Oden, J.T., Vemaganti, K., and Moes, N., "Hierarchical Modeling of
Heterogeneous Solids," Comput. Methods Appl. Mech. Eng.,
Vol. 172, pp. 3-25, (1999).
[3] Fish, J. and Belsky, V., " Multi-grid Method for Periodic Heterogeneous
Media, Part 1: Convergence Studies for One-Dimensional Case," Comput. Methods Appl. Mech. Eng., Vol. 126, pp. 1-16, (1995).
~~~~~~~~~~~~~~~~~~~~~~~~
The large publication was recently issued by Ghoniem, N. and Kioussis, N. (2005) on the noble now topic "How to reach Multiscaling in Nanotech?" -
Nasr M. Ghoniem and Nick Kioussis, "Hierarchial Models of Nanomechanics and Micromechanics," in Handbook of Theoretical and Computational Nanotechnology; edits. Michael Rieth and Wolfram Schommers, American Scientific Publisher 1, pp. 1-97, (2005).
Because the study was positioned as like in between the Continuum Mechanics applications and The Nanotech fields related to Continuum Mechanics traditional writings, we need to address this one more "multiscaling" text. Few words we drop in the Nanotechnology section. I know the person and that is why can even place more lengthy remarks on these publications.
In p. 2 we can read the good words of intensions -
"Multiscale interconnected approaches will need to be developed to interpret new and highly specialized nano-/micromechanical tests. One of the advantages of these approaches is that, at each stage, physically meaningful parameters are predicted and used in subsequent models, avoiding the use of empiricism and fitting parameters...."
"...In this article, we review several components of mechanics that are collectively needed to design new nano and micro materials, and to understand their performance. We first discuss in Section 2 the main aspects of quantum mechanics based methods (ab initio). Concepts of statistical mechanics that permit the interpretation of modern atomistic simulation methods, such as molecular dynamics (MD) and kinetic Monte Carlo (KMC) are introduced in Section 3, together with essential details of empirical interatomic potentials and computational techniques. For a description of the mechanics of materials at length scales where defects and microstructure heterogeneities play important roles, we introduce mesomechanics in Section 4. Finally, applications of nanomechanics and micromechanics are given in Section 5."
As usual in this kind of text - there are a number of scientific techniques that had been developed during the last 60-40 years AND NOTHING about - How we can transfer our models (with their data and solutions) from one scale into another? They can not do this while using the mathematics of Continuum Mechanics which based on the Homogeneous GO theorem.
And they need to know this if not yet know - professors and then students.
What we are writing here in this website and in the "Nanotechnologies" section -
For example, in p. 39 we are reading that -
"4. COMPUTATIONAL MESOMECHANICS
4.1. Introduction
"Understanding the collective behavior of defects is important because it provides a fundamental understanding of failure phenomena (e.g., fatigue and fracture). It will also shed light on the physics of self-organization and the behavior of critical-state systems (e.g., avalanches, percolation, etc.)."
That again are all the correct words on intension, but the implementation is all about the one scale.
"In an attempt to resolve these observations, two main approaches have been advanced
to model the mechanical behavior in this meso length scale. The first is based on statistical
mechanics methods [135--142]. In these developments, evolution equations for statistical
averages (and possibly for higher moments) are to be solved for a complete description of
the deformation problem. The main challenge in this regard is that, unlike the situation
encountered in the development of the kinetic theory of gases, the topology of interacting
dislocations within the system must be included [141].
The second approach, commonly known as dislocation dynamics (DD), was initially motivated by the need to understand the origins of heterogeneous plasticity and pattern formation. An early variant of this approach (the cellular automata) was first developed by [143], and that was followed by the proposal of DD [144--147]. In these early efforts, dislocation ensembles were modelled as infinitely long and straight in an isotropic infinite elastic medium. The method was further expanded
by a number of researchers [148--152], with applications demonstrating simplified features of deformation microstructure. We will describe the main features of these two approaches in the following."
How many studies referred to in this piece and still all are based on the same homogeneous techniques.
In p.40 -
" Because of the high density of dislocations and the strong nature of their interactions, direct computer simulations of inhomogeneous plastic deformation and dislocation patterns is still unattainable. "
???? Well, that is incorrect. Not for HSP-VAT, they can not
write about everything, because they don't have qualifications!
" Even if direct computer simulations are successful in the description of these collective phenomena, it is very desirable to obtain global kinetic or thermodynamic principles for understanding the self-organization associated with plasticity at the microscale. To attain these objectives, and to enable a direct link with continuum deformation theory, the statistical mechanics approach has been advanced [135--142, 153--157]."
That's wrong, that was not been advanced - as we wrote in the "
and that's just being overcome for similar issues many years ago in HSP-VAT - in the few next rooms at the same department! Well, not directly for the Continuum Mechanics of dislocations, but for the same kind of physics disciplines.
Reading further -
"The fundamental difficulty here is that dislocations, unlike particles, are linear objects of considerable topological complexity. Hence, when concepts of statistical mechanics and the theory of rate processes are used, some level of phenomenological description is unavoidable."
Not when you can use the HSP-VAT. If you know or assume the topology then the exact models can be evaluated.
In p.44 we can read that -
"In its early versions, the collective behavior of dislocation ensembles was determined by direct numerical simulations of the interactions between infinitely long, straight dislocations [11, 143, 144, 146--152, 172--175]. Recently, several research groups extended the DD methodology to the more physical, yet considerably more complex 3D simulations. The method can be traced back to the concepts of internal stress fields and configurational forces.
The more recent development of 3D lattice dislocation dynamics by Kubin and co-workers has resulted in greater confidence in the ability of DD to simulate more complex deformation microstructure [176--183]. More rigorous formulations of 3D DD have contributed to its rapid development and applications in many systems [184--193]. We can classify the computational methods of DD into the following categories:"
Look, and what about the summary of these calculation for the really Upper next scale of this "Mesomechanics" ? Not at all - that is not describable in these above and below (averaging) homogeneous theories, but HSP-VAT allows and is inherently based on and provide for the averaging and multiscaling!
In pp.83-84 one can read -
" In this section, we investigate three different averaging methods that have been proposed to extract "equivalent" isotropic elastic constants from the full anisotropic values. Two such methods, the Voigt (V) and Reuss (R) averaging procedures, are common in general elastic deformation problems, while
the third one, the Scattergood-Bacon (S-B) procedure, has been specially used in the context of determining equilibrium shear loop configurations [286]. We will examine here the extent of agreement between isotropic PDD with the anisotropic counterpart APDD, when these three approximations are used.
In the Voigt scheme, the averaging is performed over the elastic constant tensor Cijkl, while in the Reuss scheme, it is done over elastic compliances Sijkl. Results of such averaging and relevant parameters for some anisotropic crystals are listed in [225]. All calculations reported in this section are for the case of single crystal copper (A = 3.21)."
In the p. 86 we start to read on the multilayred materials elastic one scale properties solution
"5.4.5. Nanolayered Materials
A variational form of the governing equation of motion for a dislocation loop has been developed for over-damped dislocation dynamics, where the work exerted on dislocation loop expansion is balanced by viscous dissipation [192], "
And if in this classical application on Multilayer Materials authors can not put in the truly Two Scale models and their solutions, then we would advise to turn to our -
to find out about the two-scale solutions which can
be brought to the problem of elasticity in layered materials
(superlattice).
Well, we would cite more and more useless studies and analytical
texts and find out the same 1 scale Homogeneous Mechanics tools - see
the next subsection talking on the continuing
falsification in Continuum Mechanics of Heterogeneous
(Ht) Media:
~~~~~~~~~~~~~~~~~~~~~~~~
For more balance, we would dismantle for
the same purpose the monograph in Russian, (published in English as well)
that is taught to students heavily and almost replaced old ones without compassion.
Nigmatulin, R.I., Dynamics of Multiphase
Media, Part I, Moscow, Nauka, 1987, 464 p., (in Russian).
Nigmatulin, R.I., Dynamics of Multiphase
Media, Vol. I, Revised and Augmented Edition, English edit. J.C.Friedly,
New York, Hemisphere Publish. Corp., (1991). 507 p.
This is the pretty much known and cited in Russian
literature as a "bible" of heterogeneous mixture treatments book by Nigmatulin
(1987-Russian edition; 1991- English edition).
The Gauss-Ostrogradsky theorem (named formula) is given in the book in the
second page of chapter 1 as
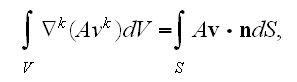
with the consequtive reference to this expression while doing derivation for
many equations.
Meanwhile, this is one of the two books in Russian, at least as I am aware
of, that gives some place to the WSAM theorem and the place to talk about the
Heterogeneous Surface - Volume transform theorem.
Also, used the consequences of
the theorem for developments. The second book in Russian is the book
by Luikov
(1971) that is the first of the kind, probably, mentioning the
WSAM theorem and deliberating on that theorem in
Russian.
1) Author, along with the solid recognition
and work on the interface phase (Z-phase, p. 43 in Russian) do not
appreciate
the fact that these phenomena are from the even lower scale than the 1-st
(Low) scale
physics in the problem. By doing this - having taken as the phenomena intact -
really included, we might improve the accuracy of phenomena accounting, etc., in
the Upper scales.
2) While establishing the general forms of
Governing equations for averaged fields (density of i-th phase, velocity, energy
and moment of phase impulse) in equations (1.2.33), (1.2.36) with more detailed
appearance in (1.2.47) - equation of impulse conservation, and (1.2.52),
(1.2.54) - equation of energy transfer, author involves the phenomena and
their mathematical interpretations of (actually) the Upper scale into the
governing equations of the Lower (homogeneous) scale.
Thus, he does this in p.55 bottom (hypothesis of small scale impulse
pulsation influence), in (1.2.44) - (1.2.46) for the form of pressure
distribution within the REV (he does not recognize the importance of the REV and
of it's specifications), in (1.2.48) - (1.2.49), (1.2.51) - the expression for
the Upper scale pulsation kinetic energy and energy exchange along the REV's
boundary?
3) Strictly speaking, author does not average
the initial homogeneous medium transport equations (1.2.1) in (1.2.25) - that is
itself incorrect as long as we need to average over the phase within the REV,
not over the phase

 th only (which is the intrinsic averaging), and the
further equations.
th only (which is the intrinsic averaging), and the
further equations.
Author hypothesises on the topic - How would be looking the one time averaged
over the

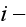 th phase governing equations for intraphase
homogeneous phenomena.
th phase governing equations for intraphase
homogeneous phenomena.
Surprisingly, when author comes to the formulation of applications we can see that he
writes, for example, in (1.3.3), (1.3.38), (1.3.45), (1.3.52), (1.3.63), 1.3.66)
the just pseudo-averaged, ad-hoc averaged equations.
These and further equations in paragraphs 4 and 5, 6,7,8,9 (the governing
equations for porous media are just unacceptable), and paragraph 10 of chapter one are
the mostly well known and used homogeneous type equations for heterogeneous
media.
Thus, unfortunately, we observe the huge gap between the mostly correct
concepts and their mathematical formulation in the paragraphs 1,2 and their
miss-implementations in paragraphs 3 -10 in chapter one. The same non-implementation of
the Upper scale averaging theory reader can find in chapters 4,5 in book 1 and
in other chapters of book 2 (Nigmatulin, 1987b; 1991b - English edition).
4) Saying this, we would be not surprized any
more why the same author (Nigmatulin R.I.), in the handling of the
sonoluminescense phenomena in the attempt to reach the nuclear fusion using the
acoustical implosion of gas bubbles in a small reservoir, see in our subsection
with comments in -
author and his co-authors used the one only scale hydrodynamic model for
obviously multiscale acoustical collapse of mutiple bubbles in a liquid.
5) The hypothesis' in (1.2.16) (author
himself calls them as such) have meaning that author suggests the free transform
from the local to an Upper scale integrated fields (nonlocal) with preserving
the properties of them. One of hypothesis is (for an arbitrary volume)
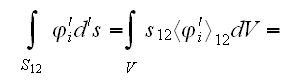
which can be re-written further as
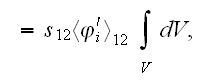
as long as according to averaging rules (1.2.13)
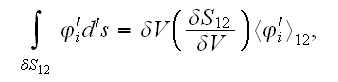
or the average interface of scalar function 
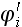 in phase
in phase 
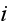 is
is
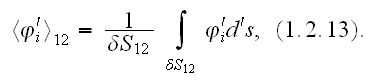
6) The equation given in p. 51 (1987a, Russian
edition) under (1.2.23) is actually the WSAM theorem while for that is not given
credit or references to authors of that theorem whatsoever in the book
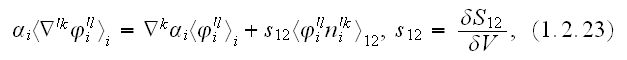
where the term
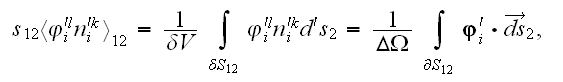
in VAT notations is no less than the very much known expression for the
interface surface integrated instant value of field's function 
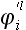 that is weighted by volume of the REV.
that is weighted by volume of the REV.
Author used to write this equation as derived via the GO theorem exploration
- that is not clear how?
Averaged over the interface 
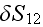 instant field
instant field 
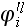 in the phase
in the phase 
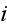 is
is
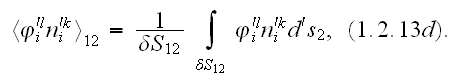
The whole this (1.2.23)
expression by Nigmatulin (1987b) means in HSP-VAT
notations the same WSAM theorem
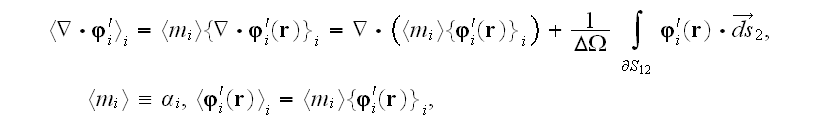
7) Few important concluding notes would be
helpful to students and professionals for appraisal and comparison of these books
by Nigmatulin (1987a,b; 1991a,b):
7.1) Author can not involve the second time
averaging into averaged equations - the second time averaging of stress - for
example, in (1.2.47) and the second time averaging of fluxes in (1.2.52),
(1.2.54).
7.2) Author does not recognize that the left
hand side of some averaged equations are wrong - (1.2.37), (1.2.47), (1.2.54).
7.3) Author does not include the turbulent
phenomena and the Lower scale turbulent initial governing equations into his
description of the concepts.
7.4) Also, there is no engagement of nonlinear
phenomena in the right hand side divergence terms in homogeneous governing
equations for the averaging process.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Weiler, F.C., "Fully Coupled Thermo-Poro-Elasto
Governing Equations,"
Proc. Computational Mechanics of Porous Materials and Their Thermal
Decomposition, ASME 1992, AMD- Vol. 136, pp. 1-28, (1992).
(author was at that time with the Lockheed Missiles and Space
Company, Palo Alto, CA )
The same city, year, and conference when I firstly spoke to American scientific
audience in San Diego
on the very part of this topic also talking on
Heterogeneous Mechanics problems while the HSP-VAT is being applied.
In abstract is said: "The objective of the present paper is to outline the
development of a set of thermo-poro-elasto governing equations which represents
the physical theory upon which new advanced rocket nozzle analysis computer
programs will be based. The three relevant areas of interest are (a) nonlinear
thermo-poro-structural analysis, (b) nonlinear pyrolysis gas flow, and (c)
nonlinear heat transfer, all of which pertain to rocket nozzle ablative
materials such as carbon-phenolics."
In spite the careful construction of the Representative Control Volume (RCV)
the analysis derived regarding the averaged stress, strain, and other functions, fields is
done as for the homogeneous medium and finally, of course, the governing equations
were done as for homogeneous statements usually performed and known from textbooks.
That did not add any value to the
program of such a scale as developing the multiphysics, multiphase transient
continuum mechanics problem.
As we said above, we can analyze like this many other "studies" and
find out the same apparatus of Homogeneous media treatments used for
Heterogeneous problems! These works above were selected based on
might be personal experiences, nevertheless, they are pretty representative ones.
Readers and students can pick up in many other places of this website
the similar things said about the "pseudo-averaging" and "multiscaling."
That's might be enough for older professionals.
The subsequent contemporary innovative and more expensive
Gatekeepers for Continuum Mechanics are described in the next subsection:
REFERENCES
Bakhvalov, N.S. and Panasenko, G.P., Homogenization: Averaging Processes in Periodoc Media.
Mathematical Problems in the Mechanics of Composite
Materials, Kluwer Acad. Publishers, Dordrecht (1989). 366 p.
Bakhvalov, N.S. and Panasenko, G.P., Averaging Processes in Periodoc Media.
Mathematical Problems of Mechanics of Composite Materials,
Nauka, Moscow, (1984). 352 p. (in Russian).
Beran, M.J., Statistical Continuum Theories,
Wiley-Interscience, New York, (1968).
Beran, M.J., "Application of Statistical Theories for the Determination of Thermal, Electrical, and Magnetic Properties of Heterogeneous Materials," in Mechanics of Composite Materials, Vol. 2, Ed. G.P. Sendeckyj, Academic Press, New York, pp. 209-249, (1974).
Berryman, J.G. "Variational Bounds on Elastic Constants for the Penetrable Sphere Model," J. Phys. D: Appl. Phys., Vol. 18, pp. 585-597,
(1985).
(This work done at Lawrence Livermore National Laboratory.
P.O. Box 808. L-200. Livermore, CA 94550).
(Sponsored by - under the auspices of the US DOE under
Contract W-7405-ENG-48 and supported specifically by the Base Technology Program
of the Earth Sciences Department.).
Borisenko, A.I. and Tarapov, I. E., Vector
Analysis and Principles of Tensor Analysis with Applications, Visshaya Shkola, Moscow, (1966) (Russian publication, 3rd edition).
Borisenko, A.I. and Tarapov, I. E., Vector
and Tensor Analysis with Applications, Prentice-Hall, Inc., Englewood Cliffs,
(1968) (English translation).
Brenner, H., "Dispersion Resulting From Flow Through
Spatially Periodic Porous Media," Phil. Trans. R. Soc. Lond., Vol. 297, pp. 81-133, (1980).
Brenner, H. and Adler, P.M., "Dispersion Resulting From Flow Through Spatially Periodic Porous Media. II. Surface and Intraparticle Transport," Phil. Trans. R. Soc. Lond., Vol. A 307, pp. 149-200, (1982).
Brenner, H. and Leal, L.G., "Conservation and Constitutive Equations for Absorbed Species Undergoing Surface Diffusion and Convection at a Fluid-Fluid Interface," J. Colloid Interface Sci., Vol. 88, pp. 136-184, (1982).
Chen, J.-S. and Mehraeen, S., "Multi-scale modelling of heterogeneous materials with fixed and evolving microstructures," Modelling Simul. Mater. Sci. Eng., Vol. 13, pp. 95--121, (2005).
Chen, J.-S. and Mehraeen, S., "Variationally Consistent Multi-Scale Modeling and Homogenization of Stressed Grain Growth," Comput. Methods Appl. Mech. Engrg., Vol. 193, pp. 1825-1848, (2004).
Happel, J. and Brenner, H., Low Reynolds Number Hydrodynamics, Sijthoff and Noordhoff, Alphen aan den Rijn, (1973).
Fish, J. and Belsky, V., " Multi-grid Method for Periodic Heterogeneous Media, Part 1: Convergence Studies for One-Dimensional Case," Comput. Methods Appl. Mech. Eng., Vol. 126, pp. 1-16, (1995).
Fish, J. and Shek, K., "Multi-scale Analysis of Composite Materials and Structures," Compos. Sci. Technol., Vol. 60, pp, 2547-2556, (2000).
Ghoniem, N.M. and Kioussis, N., "Hierarchial Models of Nanomechanics and Micromechanics," in Handbook of Theoretical and Computational Nanotechnology; edits. M. Rieth and W. Schommers, American Scientific Publisher 1, pp. 1--97, (2005).
Noronha, S.J., Huang, J., and Ghoniem, N.M., "Multiscale Modeling of the Brittle-to-Ductile-Transition," J. Nucl. Mater. 329--333, 1180--1184 (2004).
Hashin, Z., Elasticity of Random Media, Trans. Soc. Rheol., Vol. 9, pp. 381-406, (1965a).
Hashin, Z., On Elastic Behaviour of Fiber Reinforced Materials of Arbitrary Transverse Phase Geometry, J. Mech. Phys. Solids, Vol. 13, pp. 119-134, (1965b).
Hashin, Z., Theory of Fiber Reinforced Materials, NASA CR-1974 Report, Univ. Pennsylvania, Philadelphia, pp. 1-690, (1972).
Hashin, Z., Analysis of Composite Materials - A Survey, J. Appl. Mech., Vol. 50, pp.481-505, (1983).
Hill, R., "Elastic Properties of Reinforced Solids: Some Theoretical Principles," J. Mech. Phys. Solids, Vol. 11, pp. 357-372, (1963).
Hill, R., A Self-consistent Mechanics of Composite Materias, J. Mech. Phys. Solids, Vol. 13, pp. 213-222, (1965).
Hori, M. and Yonezawa, F., Statistical Theory of Effective Electrical, Thermal, and Magnetic Properties of Random Heterogeneous Materials. III. Perturbation Treatment of the Effective Permittivity in Completely Random Heterogeneous Materials, J. Math. Phys., Vol. 15, pp. 2177-2185, (1974).
Hori, M. and Yonezawa, F., Statistical Theory of Effective Electrical, Thermal, and Magnetic Properties of Random Heterogeneous Materials. IV. Effective-Medium Theory and Cumulant Expansion Method, J. Math. Phys., Vol. 16, pp. 352-364, (1975).
Hori, M. and Nemat-Nasser, S., "On Two Micromechanics Theories for Determining Micro--Macro Relations in Heterogeneous Solids," Mech. Materials, Vol.31, Issue 10, pp. 667-682, (1999).
Korn, G.A. and Korn, T.M., Mathematical Handbook for Scientists and Engineers, (2nd edn.), 599p., McGraw-Hill, New York, (1968).
Luikov, A.V., Heat- and Mass Transfer (Textbook), Moscow, Energiya, (1971). (in Russian). 560 p.
Mehraeen, S. and Chen, J.-S., "Wavelet-Based Multi-Scale Projection Method in Homogenization of Heterogeneous Media," Finite Elements in Analysis and Design, Vol. 40, pp. 1665-1679, (2004).
Mura, T., Micromechanics of Defects in Solids, Martinus Nijhoff, New York, 1987.
Nayfeh, A.H., Perturbation Methods, J. Wiley & Sons, New York, (1973).
Nayfeh, A.H., Perturbation Methods, Mir, Moscow, (1976), (in Russian).
Nemat-Nasser, S. and Hori, M., Micromechanics: Overall Properties of Heterogeneous Elasticl Solids, Lecture Notes Initiated at UCSD, (1989).
Nemat-Nasser, S. and Hori, M., Micromechanics: Overall Properties of Heterogeneous Materials, 2nd edition, Elsevier Science B.V., Amsterdam, (1999).
Nigmatulin, R.I., Fundamentals of Mechanics of Heterogeneous Media, Moscow, Nauka, 1978, (in Russian). 336p.
Nigmatulin, R.I., Dynamics of Multiphase Media, Part I, Moscow, Nauka, 1987, 464 p., (in Russian).
Nigmatulin, R.I., Dynamics of Multiphase Media, Vol. I, Revised and Augmented Edition, English edit. J.C.Friedly, New York, Hemisphere Publish. Corp., (1991). 507 p.
Nigmatulin, R.I., Dynamics of Multiphase Media, Part II, Moscow, Nauka, 1987, 360p., (in Russian).
Nigmatulin, R.I., Dynamics of Multiphase Media, Vol. 2, Revised and Augmented Edition, English edit. J.C.Friedly, New York, Hemisphere Publish. Corp., (1991). 371 p.
Oden, J.T., Vemaganti, K., and Moes, N., "Hierarchical Modeling of Heterogeneous Solids," Comput. Methods Appl. Mech. Eng., Vol. 172, pp. 3-25, (1999).
G.Papanicolaou, ed., Wave Propagation in Complex Media, Springer-Verlag, New-York, 1998. 287 p.
Russel, W.B., Saville, D.A., and Schowalter, W.R., Colloidal Dispersions, New York, Cambridge, Cambridge University Press, 1991.
Shenderova, O.A., Brenner, D.W., Nazarov, A.A., Romanov, A.E., and Yang, L.H., " Multi-scale Modeling Approach
for Calculating Grain Boundary Energies From First Principle," Phys. Rev. B, Vol. 57, (1998).
Truesdell, C., A First Course in Rational Continuum Mechanics, Baltimore, John Hopkins Univ., (1972).
Truesdell, C., A First Course in Rational Continuum Mechanics, Moscow, Mir, (1975), (in Russian).
Vaithyanathan, V., Wolverton, C., and Chen, L.Q., "Multi-scale Modeling of Precipitate Microstructure Evolution," Phys. Rev. Lett., Vol. 88, (2002).
Wagner, G.J., and Liu, W.K., "Hierarchical Enrichment for Bridging Scales and Meshfree Boundary Conditions," Int. J. Numer. Methods Engng., Vol. 50, pp. 507-524, (2000).
Wagner, G.J., and Liu, W.K., "Coupling of Atomic and Continum Simulations using a Bridging Scale Decomposition," J. Comput. Phys., Vol. 190, pp. 249-274, (2003).
Weiler, F.C., "Fully Coupled Thermo-Poro-Elasto Governing Equations," Proc. Computational Mechanics of Porous Materials and Their Thermal Decomposition, ASME 1992, AMD- Vol. 136, pp. 1-28, (1992).
Yu, Q. and Fish, J. , "Multi-scale Asymptotic Homogenization for Multi-physics Problems with Multiple Spatial and Temporal Scales: a Coupled Thermo-Viscoelastic Example Problem," Int. J. Solid Struct., Vol. 39, pp. 6429-6452, (2002).
Yau, W.W. and Kirkland, J.J., and Bly, D.D., Modern Size-Exclusion Liquid Chromatography, Wiley, New York, (1979).
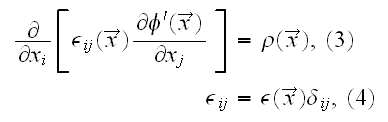
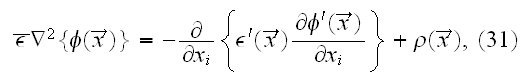
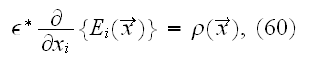
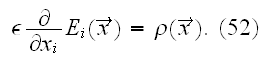
![]()
![]() from just a knowledge of low-order statistical
information."
from just a knowledge of low-order statistical
information." ![]()
![]() "
"