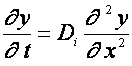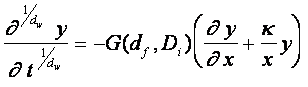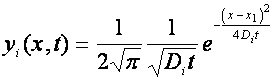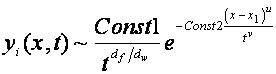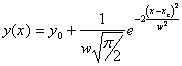The published below study is the characteristic one, where some issues concerned with the fractality claims, those “should be” present everywhere. To this extend it is appropriate to point out here, among others; the interesting discussion appeared in #279 of “Science”:

a) Biham, O., Malcai, O., Lidar, D.A., and Avnir, D., “Is Nature Fractal? (Reply to Letters by B.Mandelbrot and P.Pfeifer), Science, V. 279, p. 785, (1998)

b) Biham, O., Malcai, O., Lidar, D.A., and Avnir, D., “Fractality in Nature (Reply to a Letter by A.A.Tsonis), Science, V. 279, p. 1615, (1998)

Example of Inadequacy of Available Diffusion Theories to Describe the Transport Properties of Point-Like Objects in Multi Scale Heterogeneous Substructure

Y.G. Gordienko, V.S.Travkin*

Institute for Metal Physics, Kyiv, Ukraine

*HSPT, Chatsworth, California

Abstract

Simulation of diffusion on the basis of fractional diffusion equation was performed for investigation of anomalous transport properties in plastically deformed Al-Mg single crystals. Digitized 2D surface images were used for morphological analysis, computation of the spatial correlation functions (by calculation of “fractal” dimensions) and simulation for different scales of Al-Mg samples. On the basis of calculated fractal dimension the fractional diffusion equation was constructed and diffusion problem was numerically solved (with distribution of the given initial heterogeneous concentration of "diffusing particles" in 2D domain with periodically boundary conditions). These calculations were verified by computer simulation of diffusion in 2D rectangular lattice for different types of simulated random heterogeneous media with the same level "defect substructure content" as it was observed in Al-Mg samples. These types of media were created by random distribution of numerous parts of material substance in 2D rectangular lattice ("defect substructure content"), which have different sizes (1, 2, 4, 8, 16, 32). As a result the different types of dynamics of diffusion processes (non-Gaussian shape of average particle density or "deformed Gaussian") were observed for different media with the same "defect substructure content". The conclusion is that measures of volume fraction and uniform spatial correlation are not enough for characterization of diffusion transport properties in multiscale heterogeneous media.

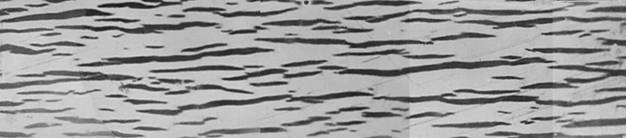
Motivation. The problem was motivated by interest in diffusion processes of point-like defects in metals under fatigue loading among band-like substructure regions, which are assumed to be impenetrable for point-like defects (Fig. 1).

The main aim is to show inadequacy of the current approaches to determine and characterize universal characteristics for anomalous diffusion. To determine universal characteristics for diffusion and investigate the physical reasons for anomalous diffusion.

Problem Formulation

Fig. 1. Initial band-like pattern on Al-Mg surface <001>{100}

For simulation of diffusion processes on this heterogeneous and anisotropic terrain we simplified the pattern with roughening the whole picture to 1-bit black-and-white pattern shown in Fig. 2.

Fig 2. High-contrast snapshot used in simulations

Then, two different diffusion problems were considered: with perpendicular (Fig. 3) and parallel (Fig. 4) mutual orientation of bands and initial source of diffusing particles.

a) whole pattern b) initial source c) final distribution of particles	a)		b)	c)
Fig. 3. Perpendicular orientation of bands and initial source		Fig. 4. Parallel orientation of bands and initial source

Analytical Solutions

In general, this simulation with symmetry along one of the axes for each case can be described by equations

a) homogeneous case, standard diffusion equation	b) heterogeneous case, fractal diffusion equation [1]

where D_i = D_^ for perpendicular and D_i = D_|| for parallel orientation,

, d_f — fractal dimension of medium, d_w —anomalous diffusion exponent (d_w= 2 for standard diffusion and d_w= 1.333 for self-avoiding walks [2]) and by definition fractional derivative is: .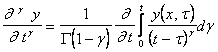

Periodic boundary conditions for torus topology are:, a>>1 and initial condition is as follows:

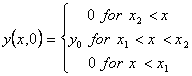
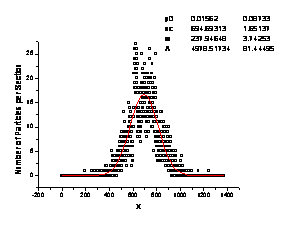
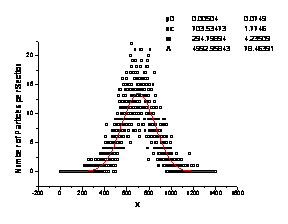
As a result in a limit x₂-x₁®0 one can obtain:

a) homogeneous case, standard diffusion equation	b) heterogeneous case, fractal diffusion equation, ,

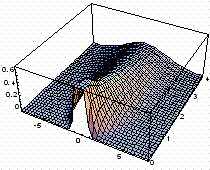
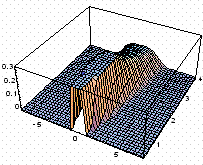
The numerical solutions are shown below for the x₂-x₁=1, y₀=1, a=5, t = [0,4], D_i=1.

	df =2, dw=1.333 (self-avoiding walks in 2D embedding space)	df =1.8, dw=2 (non-avoiding walks in fractal space)
a) standard equation	b) fractional equation

Fig. 5. Numerical solutions

Simulation Results on Perpendicular Orientation

Below simulation results on heterogeneous cases are shown in comparison with a homogeneous case (empty 2D embedding space).

a) homogeneous case
b) heterogeneous case
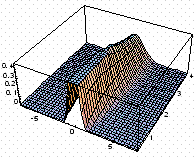
Fig. 6. Typical distributions of particles after time T
a) case homogeneous	b) heterogeneous case
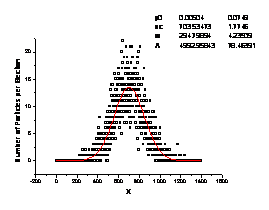
Fig. 7. Typical distributions fitted by Gaussian with parameters shown in the left upper corners

Fractal Dimension	Homogeneous	Heterogeneous
Capacity	2	1.91±.03
Information	2	1.89±.015
Correlation	2	1.87±.02

NOTE. As one can easily note all Gaussian parameters are nearly equal for this two qualitatively different morphologies and they cannot be resolved, nevertheless different fractal dimensions. The reason is availability of pronounced anisotropy of elongated substructure regions ("bands"), which cannot impede diffusion of particles along bands.

Simulation Results on Parallel Orientation

Below simulation results on heterogeneous cases are shown in comparison with a homogeneous case (empty 2D embedding space).

a) homogeneous case	b) heterogeneous case
Fig. 8. Typical distributions of particles after time T/4
a) case homogeneous	b) heterogeneous case
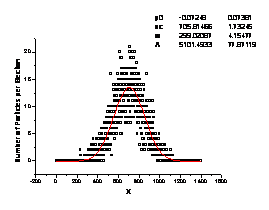
Fig. 9. Typical distributions fitted by Gaussian

NOTE. In this case two qualitatively different morphologies can be noted easily, because some Gaussian parameters are substantially different. The reason is availability of "screening" effect, which is caused by merging bands.

Continuous Transition from Heterogeneous to Homogeneous Morphology

The typical heterogeneous patterns with the same content of impenetrable phase and the same fractal dimensions 1.99±.01 are shown. They CANNOT be described adequately by the standard diffusion and modern theories of diffusion on the basis of fractional calculus.

a) smallest object 1´1
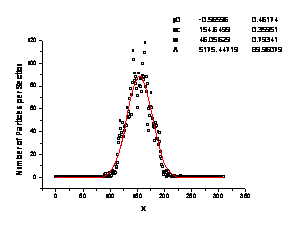
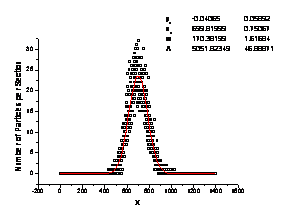
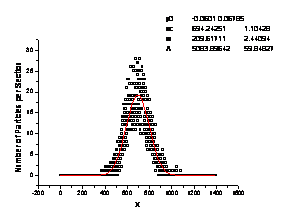
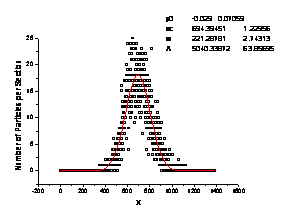
b) smallest object 4´4
c) smallest object 8´8
d) smallest object 32´32

e) empty space (smallest object ~300´300)

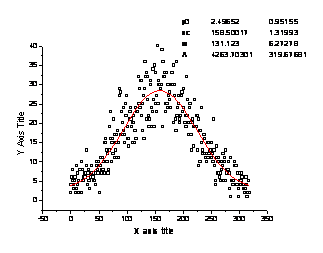
Fig. 10. Different diffusion scenarios with increasing width of peak (w)

Conclusions

— diffusion of point-like defects in anisotropic heterogeneous substructure tend to be localized along direction of "band-like" defect substructure (see Fig. 6 and 8); it can improve localizaion of evolution processes in defect substructure during further fatigue loading (which was observed in experiments [3]);

— comparison of simulated concentration profiles (see Fig. 7 and 9) with results of analytical calculations on the basis of fractional equation (Fig. 5) allows us to find INADEQUACY of the current theories of fractional calculus for description of the transport properties of point-like objects in heterogeneous substructure;

— however, for quantitative conclusion simulated domain should be extended (and it easily can be done) in the further investigation;

— the new anomalous feature was found by simulations for heterogeneous patterns with the same content of impenetrable phase, the same fractal dimension (which is »2), but with different sizes of randomly distributed impenetrable obstacles (Fig. 10); it consists in impeded diffusion for the patterns with the smaller obstacles. We assume that in the case the finer impenetrable substructure contains multiscale structure, for example lagoons of linked obstacles ("traps") and particles have to visit the same places (in traps) much frequently than other ones (outside traps).

— that is why we conclude about necessity to improve the well-known fractional diffusion equations by taking into account the scales of the heterogeneous substructure.

References

1. B.B.Mandelbrot, C.J.G.Evertsz, and Y.Hayakawa, Phys. Rev. A42 (1990) 4528.

2. L.Peliti, Random Walks with Memory, in Fractals in Physics (Russian translation), (Moscow: Mir: 1988).

3. E.E.Zasimchuk and Yu.G.Gordienko, to be published.

4. B.B.Mandelbrot, J.Fluid.Mechanics., 62 (1974) 331.

5. A.Bunde and S.Havlin, (eds.) Fractals and Disordered Systems, (Springer-Verlag: Berlin: 1991).