
The material for internal combustion engine porous insert thermal recuperator (composite media) study was chosen from the few seems most appropriate for the topic of Industrial Engineering applications of HSP-VAT.
The study was not properly performed along of HSP-VAT direction, due to few reasons. One of them was that many participants were silently or openly objected involvement of HSP-VAT for the direct estimations and design - as of too much for it. Another reason was, as always, the lack of money, time and of qualified personnel.
We will talk here about the samples of SiC porous foam

manufactured and supplied to us (Morrin-Martinelli-Gier Memorial Heat Transfer Laboratory at UCLA, 1995-96) by Ultramet
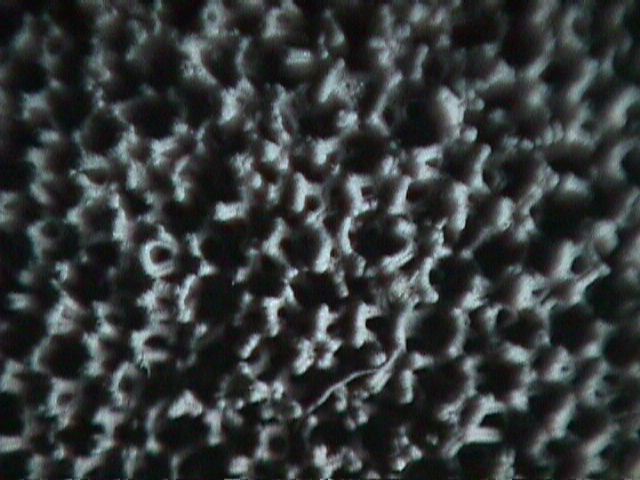

the less porous sample

featured with the hundreds micron scale microscopic picture

and with the micrometer scale microscopic picture
While lastly we would demonstrate one sample with the consecutively shown scaled pictures down to the nanoscale showing the structure of the ligaments - those are having the heterogeneity features at every scale
The substantial portion of HSP-VAT needed morphological studies were performed in collaboration with and by Dr. Yu.G.Gordienko of the Institute of Metal Physics of the National Academy of Sciences (Ukraine).

We will talk later on the morphology results.
The foamy recuperator structure was sought to be in periodical actions which would subject the porous medium mostly through the variety of flow regimes well, of coarse, mostly in the high numbers turbulent range. The steady state VAT based 1D governing equation for laminar momentum transport in porous media(Travkin and Catton, 1998) is
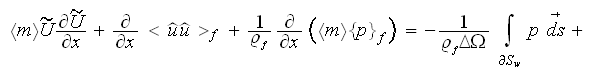
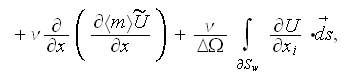
along with the momentum equation for turbulent flow of an incompressible fluid
in porous media based on K-theory form (Gratton et al., 1995, Travkin and
Catton, 1995)
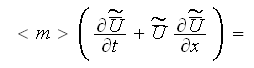
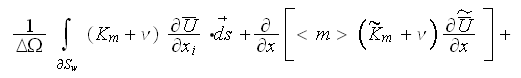
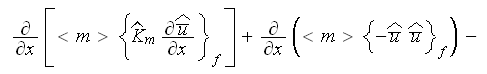
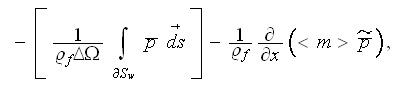
while these complicated equations for the steady-state internal domains with
homogeneous porosities can be cut to the one-dimensional momentum equations
for a regular porous media as
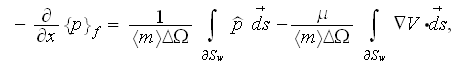
and
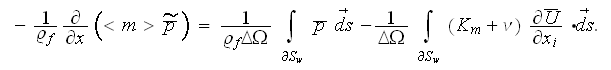
The closure of these integral terms we are considering elsewhere in this website, more in - "Fluid Mechanics Experiments Example - the Flow Resistance in Porous and Virtually Porous (Obstructed) Media"
When the porosity is constant, the flow is laminar and

 ,
the equation becomes
,
the equation becomes
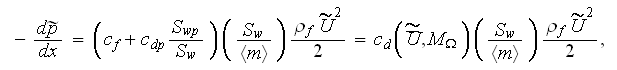
where

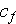 is the friction factor and
is the friction factor and

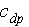 the form drag,
the form drag,

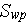 is the cross flow form drag specific surface and
is the cross flow form drag specific surface and

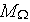 is a set of porous medium morphological parameters or descriptive functions
(see Travkin and Catton, 1992; 1995). The drag terms can be combined for
simplicity into a single total drag coefficient to model the flow resistence
terms in the general simplified momentum VAT equation
is a set of porous medium morphological parameters or descriptive functions
(see Travkin and Catton, 1992; 1995). The drag terms can be combined for
simplicity into a single total drag coefficient to model the flow resistence
terms in the general simplified momentum VAT equation
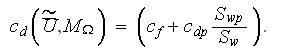
Correlations for drag resistance can be evaluated for a homogeneous porous
media from experimental relationships for pressure drop. For example, the
equation often used for packed beds is
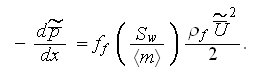
From this one can easily develop the nonlinear permeability coefficient for
the Darcy dependency
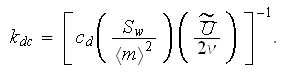 Often
used in experiments the two term quadratic Reynolds-Forchheimer pressure loss
correlation
Often
used in experiments the two term quadratic Reynolds-Forchheimer pressure loss
correlation
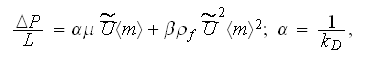 can
be compared with the simplified VAT (SVAT) momentum equation for constant
morphological characteristics and flow field properties and the resistance
coefficient
can
be compared with the simplified VAT (SVAT) momentum equation for constant
morphological characteristics and flow field properties and the resistance
coefficient

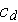
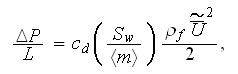 then
a set of transfer relationships can be found to transform Ergun type
correlations and the SVAT expression. The transfer formula (Travkin and
Catton, 1998) is
then
a set of transfer relationships can be found to transform Ergun type
correlations and the SVAT expression. The transfer formula (Travkin and
Catton, 1998) is
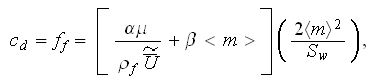 where
where
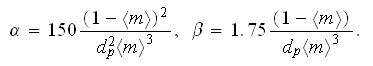 or
or
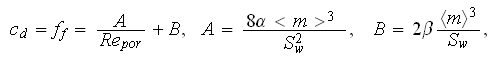 where
where
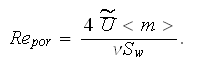 The
Ergun energy friction factor relation can be written in terms of the VAT based
formulae
The
Ergun energy friction factor relation can be written in terms of the VAT based
formulae
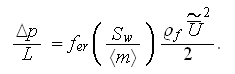 If the Ergun correlation is written using common notation, it becomes
If the Ergun correlation is written using common notation, it becomes
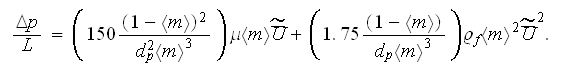
Following this simplified VAT (SVAT) analysis the data were sought for the pressure loss coefficients for the SiC ceramic foam samples.
Experimental data for the bulk pressure loss (including the input-output drag
resistance) were obtained at UCLA lab for the 100ppi sample of SiC ceramic
foam of thickness

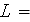 1/2
1/2
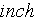 =0.0254/2=0.0127
=0.0254/2=0.0127
![$[m]\ $](case-study__29.png) and
were reduced to the following correlation
and
were reduced to the following correlation
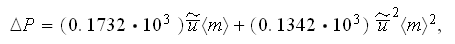
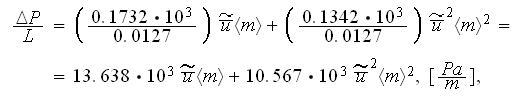
meaning that one can get in the two term steady state bulk pressure loss
equation
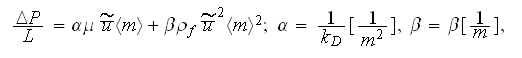
coefficients

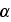 and
and

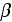 to be estimated using the dynamic viscosity and density values of a dry air
(used in the experiment as the working fluid) which are
to be estimated using the dynamic viscosity and density values of a dry air
(used in the experiment as the working fluid) which are

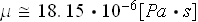

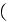 or
or

![$[kg/(m\cdot s)])$](case-study__37.png) (taking that
(taking that

 ), and
), and

 1.205
[
1.205
[
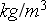 ]
at the normal conditions
P=1.013
]
at the normal conditions
P=1.013
![$\cdot 10^5[Pa]$](case-study__41.png) and T=20[C]
and T=20[C]
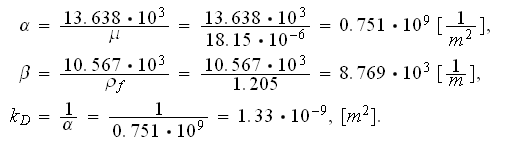
This value of

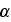 is of some variance from the
is of some variance from the

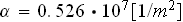 found by Beavers and Sparrow (1969) for a metal foam. Further calculations
will add some estimates to the main foam morphological characteristics and
transport parameters. From the Kozeny-Carman pressure loss model follows that
the specific surface could be estimated as
found by Beavers and Sparrow (1969) for a metal foam. Further calculations
will add some estimates to the main foam morphological characteristics and
transport parameters. From the Kozeny-Carman pressure loss model follows that
the specific surface could be estimated as
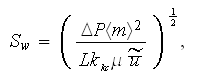
where the Kozeny-Carman constant can be taken as

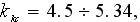 so if the next points are taken from the experimental correlation curve as
so if the next points are taken from the experimental correlation curve as

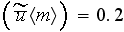 at
at

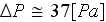 and the porosity is
and the porosity is

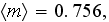 and
and

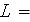 1/2
1/2
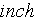 =0.0254/2=0.0127
=0.0254/2=0.0127
![$[m]$](case-study__52.png) then
then
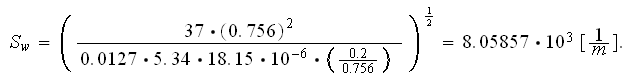
Then can be estimated the hydraulic diameter as
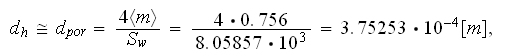
which looks rather close to the value of

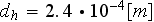 taken from the preliminary studies.
taken from the preliminary studies.
The value of specific surface

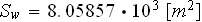 can be used in an estimation of the Darcy coefficient of permeability
can be used in an estimation of the Darcy coefficient of permeability

 throught the Kozeny-Carman model
throught the Kozeny-Carman model
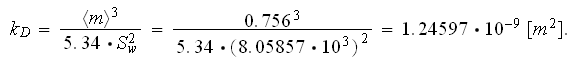
The latest value looks pretty close to the former one

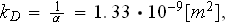 obtained
in (). This is very incouraging fact because the numbers were obtained through
the different pressure loss models. The Fanning friction factor
obtained
in (). This is very incouraging fact because the numbers were obtained through
the different pressure loss models. The Fanning friction factor

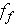 calculated
using the derived in 2.1.2 formulae and estimated above characteristics will
be
calculated
using the derived in 2.1.2 formulae and estimated above characteristics will
be
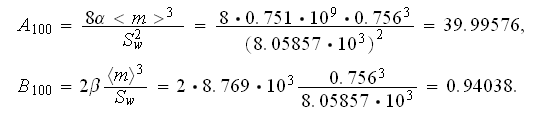
where for the 100ppi sample foam studed
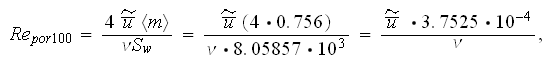
and finally the SVAT (Fanning) friction factor is
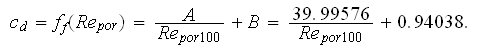
Thus, when applying obtained at UCLA the experimental correlation reformulated
for simplified VAT 1D momentum equation one has the expression for the bulk
pressure loss in the SiC foam at 100ppi which should be used with obtained
values for

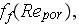

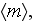 and
and

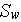
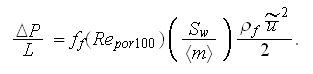
The rude quick method for approximation of morphological parameters estimation
based on the foam material 2D cross-section images and suggested above
procedures can be consisting of the following steps. The estimation of the
hydraulic diameter using cross-section images of foam and
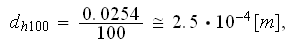
which looks close again to

 estimations presented above by the two different methods. Assuming that the
following points have no or are just below reasonable doubts when the 120ppi
foam is the working medium:
estimations presented above by the two different methods. Assuming that the
following points have no or are just below reasonable doubts when the 120ppi
foam is the working medium:
1) if porosity value

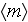 is still of the same or known value;
is still of the same or known value;
2) if morphology of the 120ppi foam medium presented is having been obtained by affinitive (homotetive) hypothetical spacial transformation from the morphology of the 100ppi foam with consiquently preserved surface and volume relationships;
3) if the input-output pressure loss dependency is preserved as of the same functional appearance as for 100ppi foam,
then one can proceed with the forecast of morphological and momentum transport parameters.
Assessing the morphological data for the ceramic SiC foam with120 ppi, first
one can get the reasonable (extrapolative) estimation for the 120ppi SiC foam
hydraulic diameter through
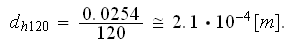
Next the specific surface can be estimated as
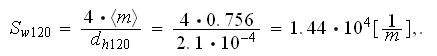
Next can be estimated the permeability coefficient using the Kozeny-Carman
model
so the low regime coefficient in the quadratic Reynolds-Forchheimer equation
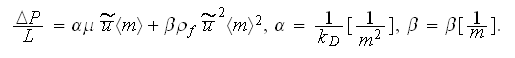
is
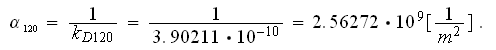
According to good correlation by Gortyshov et al. (1987) the

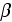 coefficient with the derived above morphological parameters for the 120ppi
foam will be
coefficient with the derived above morphological parameters for the 120ppi
foam will be
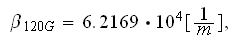
which is worth to trust because the

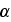 coefficient obtained through their correlation is
coefficient obtained through their correlation is
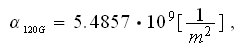
which is in a relatively good agreement with the

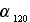 yielded by another method in (). That all means that the pressure drag
coefficient
yielded by another method in (). That all means that the pressure drag
coefficient

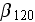 for the SiC 120ppi foam can be taken as
for the SiC 120ppi foam can be taken as
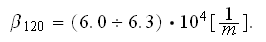
Well, using the Ergun`s drag resistance correlation we can calculate
the coefficients
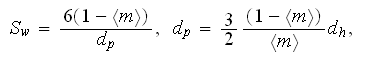
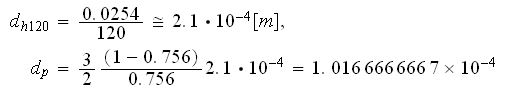
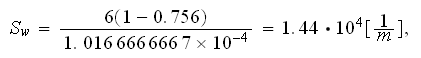
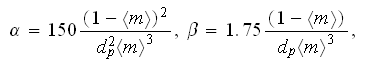
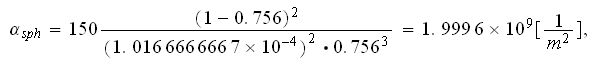
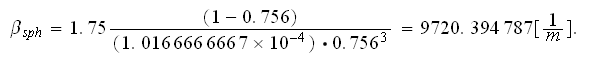
Again, we need to remind ourselves that these data should be most appropriate for the globular media and as such are not of a reputable significance for the SiC foam.
Using the coefficients for SVAT presentation of combined friction factor for
this specific sample morphology SiC 120ppi
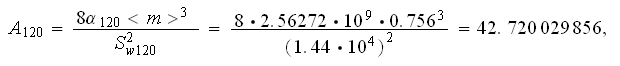 :
:

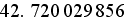
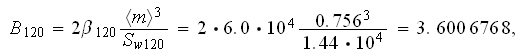
:

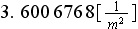
where for the 100ppi sample foam studed
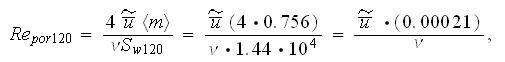

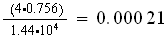
and finally the friction factor is
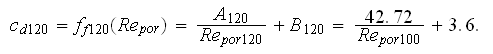
Thus, when applying the simplified VAT 1D momentum equation for the bulk
pressure loss in the SiC foam at 120ppi which should be used with obtained
values for

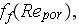

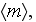 and
and

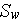

Of course, those were the estimates obtained using the low temperature working
fluid - an air. To observe the range in characteristics of engine combustion
products at the temperature T=1200[C] and still at pressure
P=0.1
![$[MPa]$](case-study__100.png) one needs to compare the data above using the values
one needs to compare the data above using the values
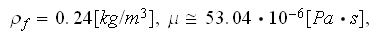
which are different in

 times from the given above data for the low room temperature for
times from the given above data for the low room temperature for
a dry air

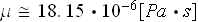

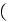 or
or

![$[kg/(m\cdot s)])$](case-study__105.png) (taking that
(taking that

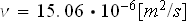 ), and
), and

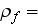 1.205
[
1.205
[
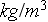 ]
at the normal conditions
P=1.013
]
at the normal conditions
P=1.013
![$\cdot 10^{5}[Pa]$](case-study__109.png) and T=20[C], and taken for estimation as approximately the same for combustion
products.
and T=20[C], and taken for estimation as approximately the same for combustion
products.
Doing this for the sample with 100ppi we could get that
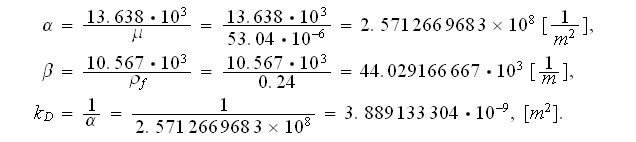
The Fanning friction factor

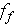 calculated
using the derived above formulae and estimated characteristics will be
calculated
using the derived above formulae and estimated characteristics will be
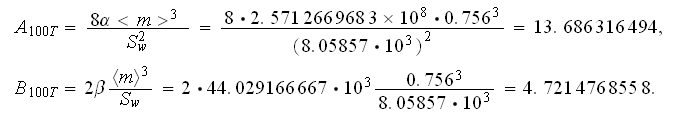
and finally the friction factor estimation for high temperature gas is
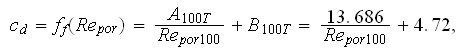
which is the large departure from findings for the room temperature estimation
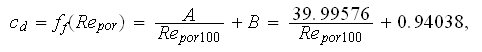
which in its turn would be used in the SVAT pressure loss dependency
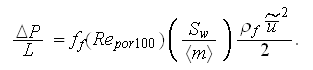
In all these data have been included the "input-output" pressure losses effect.
The laminar regime VAT 1D (most of interest for this situation) upper scale
thermal transport equations are
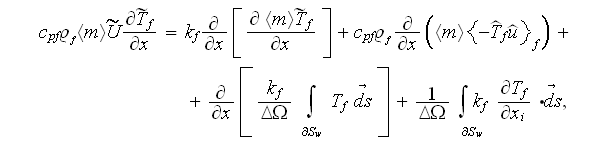
and
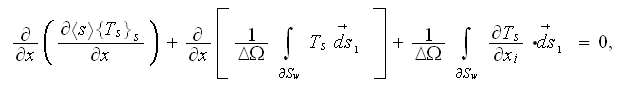
while for the turbulent (or nonlinear) heat exchange in the ceramic foam we
would use the equation
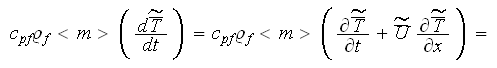
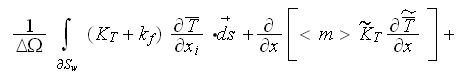
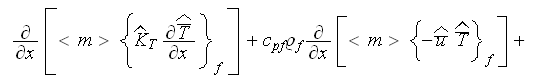
while in the solid phase, the corresponding equation is
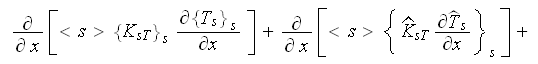
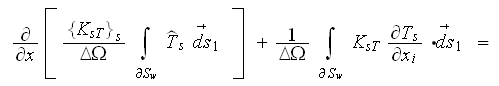
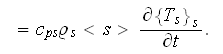
These are the very difficult to crack equation sets even at present time -
near nine years later. Meanwhile, the prevailing number of research on heat
exchange in the porous medium are done with the equation like
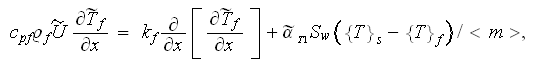
when the porosity is constant and even for the changing porosity function, even for turbulent heat exchange. So we had no resources, but used to explore that simplest equation which still has the slight resemblance and possibility to apply the VAT analysis, which was named as the Simplified VAT (SVAT) modeling analysis.
More consistent description of issues related to porous media VAT models and experiments see in - - "Heat Exchangers," - "Semiconductor Coolers" - and - "Further Reading and Consulting";
In the course of this text in this subsection we will be able to comment or undertake some level of analysis for only few most suitable for the purposes of the current application data namely - internal heat transfer coefficient for the internal combustion engine's foam ceramic regenerator. There are few obviously good reviews with regard of that matter (Kar and Dybbs, 1982; Majorov, 1978 ).
Nevertheless, as was noted by Viskanta (1995) ''Convective heat and mass transfer in consolidated porous materials has received practically no theoretical research attention. This is partially due to the complexity which arises as a result of physical and chemical heterogeneity that is difficult to characterize with the limited amount of data that can be obtained through experiments.''
The generalized data with regard to internal porous ceramic heat transfer
coefficient in most works reduced in the form (Viskanta, 1995)
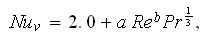
assuming that the limited Nusselt number should be of 2.0 when the Re number decreases to zero. This assumption is relatively justified for unconsolidated sparse spherical particles morphologies only and sufficiently doubtful for other porous medium morphologies especially consolidated ones. That is why some researches neglect this artificial low boundary limitation and correlating their findings neglecting low limit 2.0.
Large amount of results and data analyzed and provided by Viskanta (1995a,b) were used here to deduce few correlations with regards to current application medium heat transfer characteristics
Few of the most relevant experimental correlations were brought down with the same methodology which use the consequencies of VAT represenation of the heat transfer on both scales and then simplify them to accomodate the known and verified experimental data-correlations.
Thus, in correlation
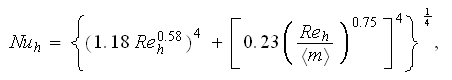

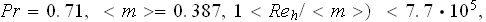 by Achenbach (1995) were used the hydraulic diameter Reynolds number which is
by Achenbach (1995) were used the hydraulic diameter Reynolds number which is
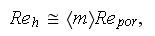 also
also
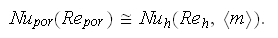
The semiempirical theory designed by Kokorev et al. (1987) to establish
correlation between resistance coefficient and heat transfer coefficient for
extensive flow regimes in porous media contains only one empirical (apparently
universal for turbulent regime) constant. On the basis of this relationship, a
concept of fluctuation speed scale of movement, is used in that theory to
determine an expression for the heat transfer coefficient through the Darcy
friction factor

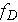 ,
which is written in terms of a hydraulic diameter is equal
,
which is written in terms of a hydraulic diameter is equal

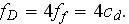 The "particle" written Nusselt number by Kokorev et al.
The "particle" written Nusselt number by Kokorev et al.
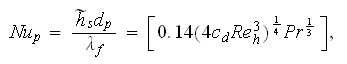
rewritten in the general scale

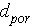 porous medium
porous medium

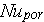 number is
number is
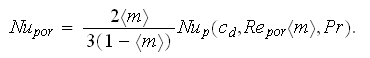
The Kay's and London relation can be presented as
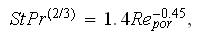
which means
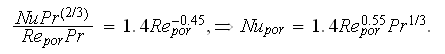
Some useful observations can be made while compare the heat transfer dependencies related in the Figure
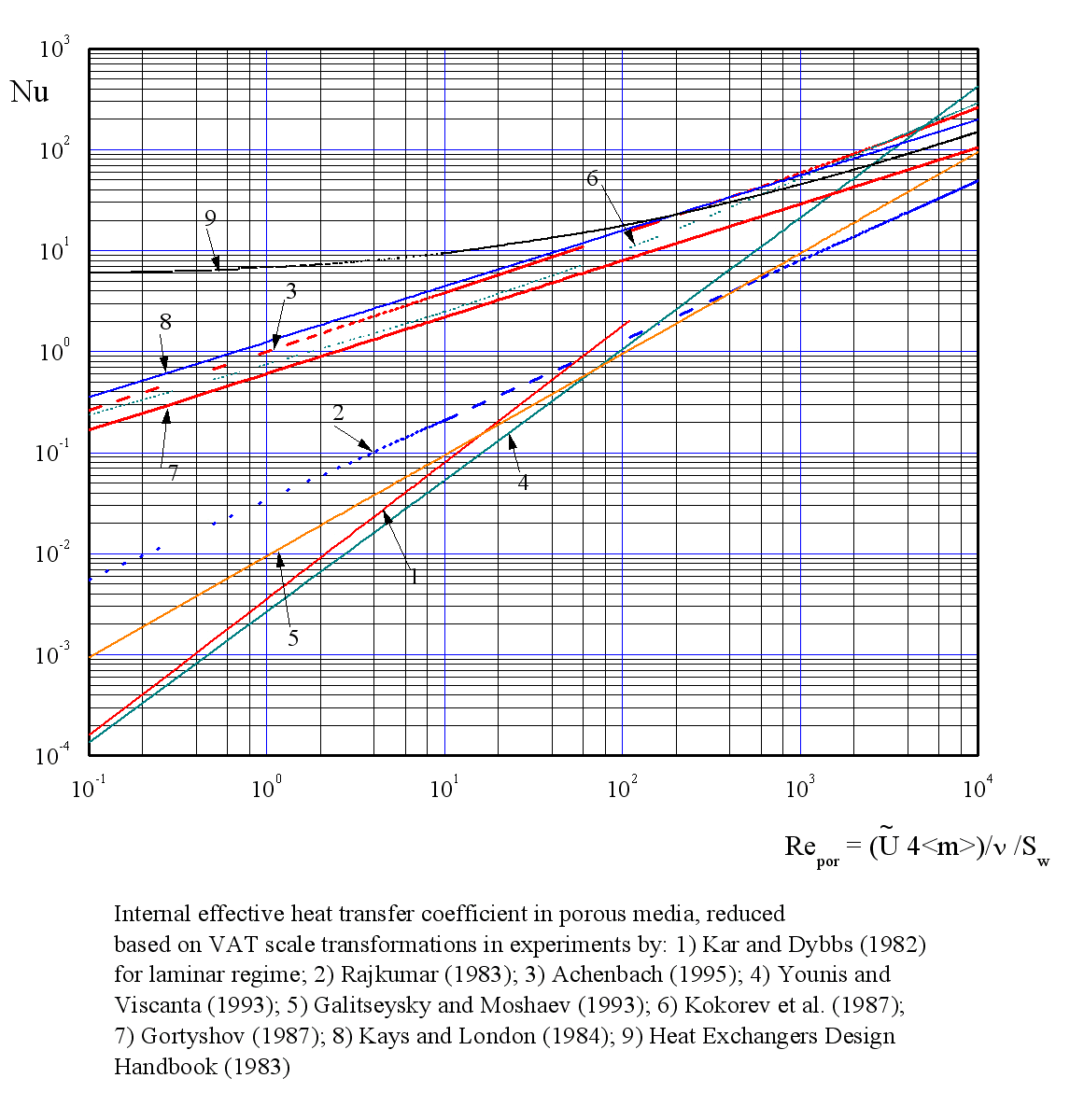
One of the most significant notes is that the difference of such a big magnitude as between the lines by Kar and Dybbs (1982), Younis and Viscanta (1993) and Rajkumar (1993) data and others couldn't be explained if one not take into account the specifics of media, design of experimental data treatment etc. In lieu of this furthermore seems as a remarkable almost coincidence of correlations by Kays and London (1984), Achenbach (1995), and Kokorev et al. (1987). Those expressions were developed using different techniques and basic approaches. The data reduction given in the Heat Exchangers Design Handbook (1983) reflects apparently a highly specialized adjustment level of this correlation in the low Reynolds bound range.
That is
why this correlation cannot be considered as based on the one specific approach (
as, for example, globular morphology with specific globular diameter) and data
reduction method but conversely as having a goal to represent somehow
summarized data on heat transfer coefficient in packed bed in a wide range of
Reynolds numbers calculated using accepted globular particles diameter. An
obvious transformation from particle to pore scale using general simple
technique as described above doesn't work properly in this case. One more
noteworthy observation could be derived on the basis of substantial, order of
magnitude, difference in the range of high

 numbers
(
numbers
(
 -
-

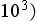 between two groups of correlations, see Figure. Also outstandingly lies the
line by correlation of Galitseysky and Moshaev (1993) presented with specific
adjustment coefficient (Viscanta, 1995b).
between two groups of correlations, see Figure. Also outstandingly lies the
line by correlation of Galitseysky and Moshaev (1993) presented with specific
adjustment coefficient (Viscanta, 1995b).
The recommendations expressed here are based only on the SVAT analysis which gave us ability to perform and compare very different experiments and experimental correlations. Using data and methods of calculation of these data in the Figure the observation can be made in the favor of three correlations, namely by Kays and London (1984) (modified), Achenbach (1995), and Kokorev et al. (1987) those were justified for to be used in modeling simplified equation, which I even hesitate to name as the VAT related
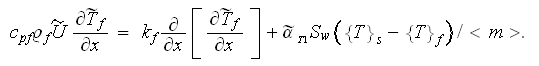
This equation was used for a quite time in thermal physics before the VAT was unveiled in its development.
Nevertheless, the closeness of some correlations' predictions revealed while comparing the known experimental data still is the simple reflection of the bulk consideration which had been applied for their derivation.
Noteworthy to mention, that all these parametric functions above presenting the lump sum of the "inside the sample" and the "input- and output" of the sample presure resistances and heat exchange coefficients.
The most appropiate method to assess the properties during design would be to separate these three, because all the evidencies speak about substantial differences between values of these resistances, heat transfer coefficients, and of their comparative input to the total assessment values. Further investigations of the SiC foam thermal and momentum transport characteristics were lacked of external funding.
Local internal porous media heat transfer characteristics are hard to find out and achieve at present moment. We need to consider at least the more complete heterogeneous modeling VAT equations and create the new techniques for the two scale measurements. This is done at present time in only the one instance - when studying the semiconductor HE spatial structures, as the two-scale measurement-modeling for Compact Heat Exchangers, see more in -

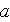 -
thermal diffusivity
[
-
thermal diffusivity
[
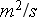 ]
]

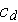 - mean drag resistance coefficient in the REV [-]
- mean drag resistance coefficient in the REV [-]

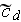 - mean skin friction coefficient over the turbulent area of
- mean skin friction coefficient over the turbulent area of

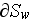 [-]
[-]

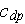 - mean form resistance coefficient in the REV [-]
- mean form resistance coefficient in the REV [-]

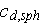 - drag resistance coefficient upon single sphere [-]
- drag resistance coefficient upon single sphere [-]

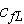 - mean skin friction coefficient over the laminar region inside of the REV
[-]
- mean skin friction coefficient over the laminar region inside of the REV
[-]

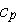 - specific heat
[
- specific heat
[
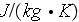 ]
]

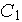 - constant coefficient in Kolmogorov turbulent exchange coefficient
correlation [-]
- constant coefficient in Kolmogorov turbulent exchange coefficient
correlation [-]

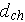 - character pore size in the cross section
[
- character pore size in the cross section
[
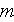 ]
]

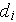 - diameter [m] of i-th pore
[
- diameter [m] of i-th pore
[
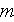 ]
]

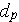 - particle diameter
[
- particle diameter
[
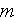 ]
]

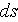 - interphase differential area in porous medium
[
- interphase differential area in porous medium
[
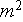 ]
]

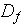 - molecular diffusion coefficient
- molecular diffusion coefficient

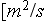 ],
also - tube or pore diameter
[
],
also - tube or pore diameter
[
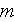 ]
]

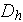 - flat channel hydraulic diameter
[
- flat channel hydraulic diameter
[
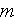 ]
]

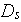 -diffusion coefficient in
solid[
-diffusion coefficient in
solid[
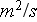 ]
]

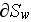 - internal surface in the REV
[
- internal surface in the REV
[
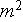 ]
]

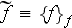 - averaged over
- averaged over

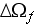 value
value

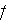 - intrinsic averaged variable
- intrinsic averaged variable

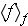 - value f, averaged over
- value f, averaged over

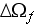 in a REV - phase averaged variable
in a REV - phase averaged variable

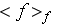 - value
- value

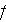 ,
averaged over
,
averaged over

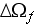 in a REV
in a REV

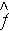 - morpho-fluctuation value of
- morpho-fluctuation value of

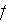 in a
in a

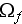

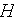 - width of the channel
[
- width of the channel
[
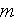 ]
]

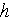 - averaged heat transfer coefficient over
- averaged heat transfer coefficient over

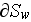 [
[
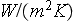 ],
half-width of the channel
[
],
half-width of the channel
[
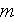 ]
]

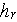 - pore scale microroughness layer thickness
[
- pore scale microroughness layer thickness
[
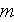 ]
]

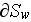 - internal surface in the REV
[
- internal surface in the REV
[
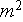 ]
]

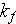 - fluid thermal conductivity
[
- fluid thermal conductivity
[
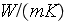 ]
]

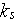 - solid phase thermal conductivity
[
- solid phase thermal conductivity
[
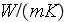 ]
]

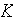 - permeability
[
- permeability
[
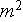 ]
]

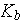 - turbulent kinetic energy exchange coefficient
[
- turbulent kinetic energy exchange coefficient
[
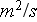 ]
]

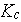 - turbulent diffusion coefficient
[
- turbulent diffusion coefficient
[
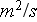 ]
]

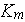 - turbulent eddy viscosity
[
- turbulent eddy viscosity
[
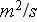 ]
]

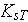 - effective thermal conductivity of solid phase
[
- effective thermal conductivity of solid phase
[
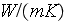 ]
]

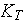 - turbulent eddy thermal conductivity
[
- turbulent eddy thermal conductivity
[
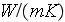 ]
]

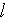 - turbulence mixing length
[
- turbulence mixing length
[
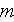 ]
]

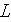 - scale
[
- scale
[
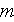 ]
]

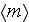 - averaged porosity [-]
- averaged porosity [-]

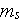 - surface porosity [-]
- surface porosity [-]

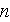 - number of pores [-]
- number of pores [-]

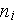 - number of pores with diameter of type i [-]
- number of pores with diameter of type i [-]

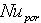 -
=
-
=
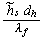 ,
interface surface Nusselt number [-]
,
interface surface Nusselt number [-]

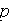 - pressure
[
- pressure
[
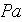 ];
or pitch in regular porous 2D and 3D medium
[
];
or pitch in regular porous 2D and 3D medium
[
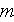 ];
or phase function [-]
];
or phase function [-]

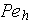 -
=
-
=
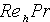 ,
Darcy velocity pore scale Peclet number [-]
,
Darcy velocity pore scale Peclet number [-]

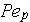 -
=
-
=
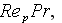 particle
radius Peclet number [-]
particle
radius Peclet number [-]

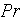 -
=
-
=

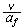 ,
Prandtl number [-]
,
Prandtl number [-]

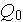 - outward heat flux
[
- outward heat flux
[
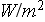 ]
]

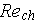 - Reynolds number of pore hydraulic diameter [-]
- Reynolds number of pore hydraulic diameter [-]

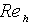 -
=
-
=
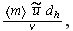 Darcy velocity Reynolds number of pore hydraulic diameter [-]
Darcy velocity Reynolds number of pore hydraulic diameter [-]

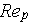 -
=
-
=
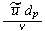 ,
particle Reynolds number [-]
,
particle Reynolds number [-]

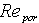 -
=
-
=
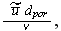 Reynolds number of general scale pore hydraulic diameter [-]
Reynolds number of general scale pore hydraulic diameter [-]

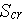 - total cross sectional area available to flow
[
- total cross sectional area available to flow
[
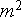 ]
]

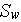 - specific surface of a porous medium
- specific surface of a porous medium

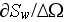 [
[
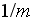 ]
]

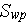

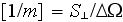

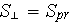 - cross flow projected area of obstacles
[
- cross flow projected area of obstacles
[
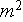 ]
]

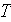 - temperature
- temperature

![$[K]$](case-study__246.png)

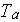 - characteristic temperature for given temperature range
- characteristic temperature for given temperature range

![$[K] $](case-study__248.png)

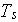 - solid phase temperature
- solid phase temperature

![$[K]$](case-study__250.png)

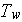 - wall temperature
- wall temperature

![$[K]$](case-study__252.png)

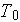 - reference temperature
- reference temperature

![$[K]$](case-study__254.png)

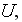

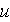 - velocity in x-direction
- velocity in x-direction

![$[m/s]$](case-study__257.png)

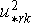 - square friction velocity at the upper boundary of hr averaged over surface
- square friction velocity at the upper boundary of hr averaged over surface

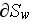 [
[
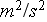 ]
]

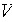 - velocity
- velocity

![$[m/s]$](case-study__262.png)

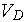 -
=
-
=
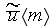 Darcy
velocity
[
Darcy
velocity
[
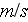 ]
]

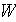 - velocity in z-direction
- velocity in z-direction

![$[m/s]$](case-study__267.png)

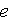 - effective
- effective

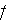 - fluid phase
- fluid phase

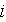 - component of turbulent vector variable; or species or pore type
- component of turbulent vector variable; or species or pore type

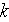 -
component of turbulent variable that designates turbulent ''microeffects'' on
a pore level
-
component of turbulent variable that designates turbulent ''microeffects'' on
a pore level

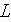 - laminar
- laminar

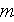 - scale value or medium
- scale value or medium

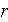 - roughness
- roughness

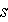 - solid phase
- solid phase

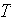 - turbulent
- turbulent

 - wall
- wall

 -
value in fluid phase averaged over the REV
-
value in fluid phase averaged over the REV

 -
value in solid phase averaged over the REV
-
value in solid phase averaged over the REV

 -
mean turbulent quantity
-
mean turbulent quantity

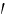 -turbulent fluctuation value
-turbulent fluctuation value

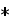 -equilibrium values at the assigned surface or complex conjugate variable
-equilibrium values at the assigned surface or complex conjugate variable

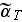 -
averaged heat transfer coefficient over
-
averaged heat transfer coefficient over

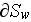

![$[W/(m^2K)]$](case-study__285.png)

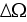 -
representative elementary volume (REV)
-
representative elementary volume (REV)

![$[m^3]$](case-study__287.png)

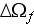 - pore volume in a REV
- pore volume in a REV

![$[m_3]$](case-study__289.png)

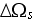 - solid phase volume in a REV
- solid phase volume in a REV

![$[m_{3}]$](case-study__291.png)

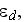

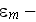 electric permittivity [Fr/m]
electric permittivity [Fr/m]

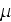 - dynamic viscosity
[
- dynamic viscosity
[
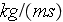 ]
or
[
]
or
[
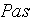 ]
]

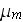 - magnetic permeability [H/m]
- magnetic permeability [H/m]

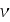 - kinematic viscosity
[
- kinematic viscosity
[
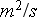 ];
also
];
also

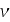 - frequency [Hz]
- frequency [Hz]

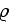 - density
[
- density
[
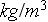 ];
also
];
also

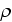 - electric charge density
[C/m
- electric charge density
[C/m
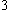 ]
]

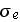 - medium specific electric conductivity [A/V/m]
- medium specific electric conductivity [A/V/m]

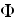 - electric scalar potential [V]
- electric scalar potential [V]

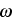 - angular frequency [rad/s]
- angular frequency [rad/s]

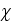 - magnetic susceptibility [-]
- magnetic susceptibility [-]
Kar, K.K. and Dybbs, A. (1982) "Internal Heat Transfer Coefficients of Porous Metals," in Heat Transfer in Porous Media, edited by J.V.Beck and L.S.Yao, ASME, New York, HTD-Vol.22, pp. 81-91.
Majorov, V.A., (1978) ''Flow and Heat Transfer of Single-Phase Coolant in Porous Cermet Materials,'' Thermal Engineering, Vol. 25, No. 1, pp.59-65.
Viskanta, R, (1995a) ''Modeling of Transport Phenomena in Porous Media Using a Two-Energy Equation Model,'' in Proceedings of the ASME/JSME Thermal Engineering Joint Conference, 1995, Vol. 3, pp. 11-22.
Viskanta, R, (1995b) ''Convective Heat Transfer in Consolidated Porous Materials: a Perspective,'' in Proceedings of the Symposium on Thermal Science and Engineering in Honour of Chancellor Chang-Lin Tien, 1995, pp. 43-50.
Achenbach, E. (1995) ''Heat and Flow Characteristics in Packed Beds,'' Experimental Thermal and Fluid Science, Vol. 10, pp. 17-21.
Rajkumar, M. (1993) ''Theoretical and Experimental Studies of Heat Transfer in Transpired Porous Ceramics,'' MSME Thesis, Purdue University, West Lafayette, Indiana.
Younis, L.B. and Viskanta, R. (1993a) ''Experimental Determination of Volumetric Heat Transfer Coefficient Between Stream of Air and Ceramic Foam,'' Intern. J. Heat Mass Transfer, Vol. 36, pp. 1425-1434.
Younis, L.B. and Viskanta, R. (1993b) ''Convective Heat Transfer Between an Air Stream and Reticulated Ceramic,'' in Multiphase Transport in Porous Media 1993, Edited by R.R.Eaton et al., ASMEl, New York, FED-Vol. 173, pp. 109-116.
Galitseysky, B.M. and Moshaev, A.P. (1993) ''Heat Transfer and Hydraulic Resistance in Porous Systems,'' in Experimental Heat Transfer, Fluid Mechanics and Thermodynamics: 1993, edited by M.D.Kelleher et al., Elsevier Science Publishers, New York, pp. 1569-1576.
Heat Exchanger Design Handbook (1983), (Spalding, B.D., Taborek, J., Armstrong, R.C. and et al., contribs.), N.Y., Hemisphere Publishing Corporation, Vol.1,2.
Kokorev, V. I., Subbotin, V. I., Fedoseev, V. N., Kharitonov, V.V., and Voskoboinikov, V.V. (1987) ''Relationship Between Hydraulic Resistance and Heat Transfer in Porous Media,'' High Temperature, Vol. 25, No. 1, pp. 82-87.
Kays, W.M. and London, A.L. (1984) Compact Heat Exchangers, 3rd ed., McGraw-Hill.
Gortyshov, Yu.F., Muravev, G.B., and Nadyrov, I.N. (1987) ''Experimental Study of Flow and Heat Exchange in Highly Porous Structures ,'' Engng.-Phys. Journal, Vol. 53,No. 3, pp. 357-361, (in Russian).
Gortyshov, Yu.F., Nadyrov, I.N., Ashikhmin, S.R., and Kunevich, A.P. (1991) ''Heat Transfer in the Flow of a Single-Phase and Boiling Coolant in a Channel with a Porous Insert, '' Engng.-Phys. Journal, Vol. 60, No. 2, pp. 252-258, (in Russian).
G.S.Beavers and E.M.Sparrow, (1969) "Non-Darcy Flow Through Fibrous Porous Media," J. Applied Mechanics, Vol. 36, pp. 711-714.