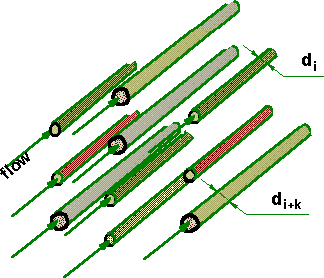
Capillary morphology model of porous medium: straight parallel pores (tubes) each having its own flow regime (generally the three types possible - the laminar, the turbulent and the intermediate one)
The Annals of Frontier and Exploratory Science
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany, Denver, CO, USA
There are two reasons why these problems demand a fundamental attention:
1) These classical problems (straight capillary, single diameter globular morphologies, and roughness of different kinds over the standing alone surface or a wall in a channel) are already for more then hundred years present the examples of pure statement of the test-problem. Few generations of researchers have been trying to solve these problems, but haven't obtained a final solution that includes both laminar and turbulent flow regimes in the pores.
For example, the solutions given in textbooks for straight capillary morphology are only for the laminar momentum transport Upper Scale one diameter pores. We published in 1998 the first ever solution for the three regimes 2-scale two-phase capillary pore distributions, some even in analytical form. This solution was not achieved since the XVIII. Further, the conjugate problem of heat transport in capillary systems has neither been stated fully nor correctly. Our studies referred to below are the solutions for both scales (Lower and Upper) and directly explain how these problems can be treated using the general HSP-VAT governing equations.
2) To help those who are working in the field, or are just interested, to obtain familiarity with the simplest multi-scale problems and give them an understanding how to correctly state the HSP-VAT problem and what are the possibilities to treat one.
Volume Averaging Theory (VAT) has been shown to be an effective and rigorous approach for study of transport (laminar and turbulent) phenomena in porous media. To better understand the mechanisms of transport phenomena in porous media, pore level network modeling of porous media was used to solve the problems of classical descent. A simplest pore level network model for a porous media is a model of straight capillary pores. VAT was successfully applied to this simple pore network before. The primary difficulty in applying VAT to straight capillary networks is the many unknown integral and differential terms that are needed for closure. Applying VAT to pore level transport in straight capillaries results in two sets of different scale governing equations. One scale is the upper scale VAT equations, which describe ensemble properties for flow and heat transfer in porous media. The other scale is the lower scale laminar and turbulent transport equations, which are for flow and heat transport in each pore capillary and in surrounding solid. It has been shown how those unknown VAT terms in the upper scale equations could be found through the relationships between upper scale VAT equations and lower scale exact solution of properties.
In other words, the closure of upper scale governing equations can be achieved exactly even analytically for laminar regime, and exactly numerically for turbulent transport. We will demonstrate the development of exact closures and mathematical procedures for the turbulent regime, extending the previous laminar regime work.
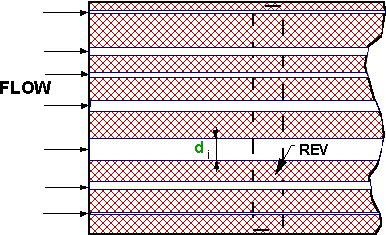
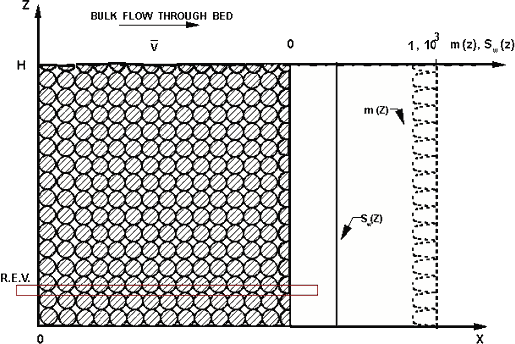
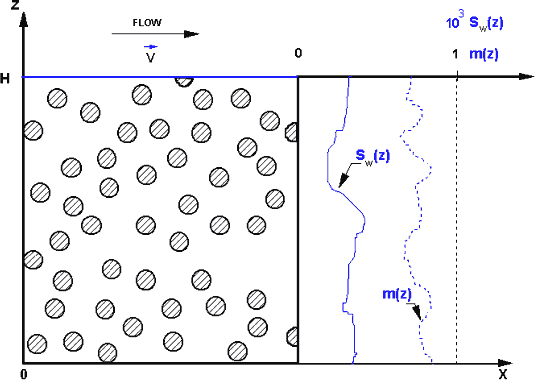
Volume averaging is a technique in which a macroscopic upper scale VAT momentum equation is derived from Navier-Stokes or turbulent equations averaged over a representative elementary volume (REV). During the averaging process, hydrodynamic information from the pore scale is retained, but it is reintroduced in the form of unknown surficial and fluctuations terms that can be determined experimentally or derived exactly for simple pore structures.
One popular pore level model to study the porous media is the network model. Network models use a series of interconnected nodes and bonds with distributed sizes. In the network model the pore space is represented as a graph of connected sites. A common interpretation of this graph is that the sites correspond to pore bodies, and the bonds correspond to pore throats connecting the pore bodies. In principle, a network model can replicate both the geometry and topology of pore space, so that flow through the network is equivalent to flow through the actual porous medium.
There are many network models. The distinction between various network models lies primarily in the choice of lattice arrangement, node and bond geometry, and in the specific solution algorithm used. The parameters that dictate a network's geometry are its spatial dimension (i.e., 2-D or 3-D), grid pattern (which maybe regular or irregular), bond-size distribution, and coordination number (the value and whether it is constant). The development of network model for flow in porous media began with Fatt (1956) who used an equivalent resistor network to calculate properties like capillary pressure, relative permeability, and resistance. Since then, numerous studies have been carried out with increasingly sophisticated rules to describe capillary equilibrium and simultaneous flow of fluids, such as Goode and Ramakrishnan (1993), Thompson and Fogler (1997), Rieckmann and Keil (1997) and Thauvin and Mohanty (1998).
To develop valid VAT equations, a straight capillary network will be our starting point. It is a very simple network. The advantage of this network is that flow and heat transfer in each pore could be easily simulated. Using the exact results in each pore, the VAT equations could be easily simulated, and the exact closures for VAT equations could be developed. In this paper, the capillary morphology shown in Fig. 1 is used as a morphology model for volume averaged network model development. Travkin and Catton (1999) demonstrated a two-scale solution for volume averaging theory (VAT) model of momentum transport in a simple case of straight parallel pore medium (SPPM). For heat transfer in a network morphology, the temperature field is not homogeneous. Two-scale solution for energy transport is gained.
The problem of lower scale heat transport in straight capillary is a conjugate problem. The analytical methods of solution of conjugated problems presented by Luikov et al. (1970) and Luikov (1974) are used in this paper for solving lower scale conjugated convective heat transfer problems. Previous studies have shown that VAT models are effective for the study of upper scale heat transport in straight capillary morphology, see Zanotti and Carbonell (1984) and Yuan et al. (1991). But the approach used in this VAT implementation to formulate closure and to find solution of current VAT problem is essentially following publication by Travkin and Catton (1998) (and earlier studies), and different to those previous works based on consideration mainly of upper scale VAT equations.


Capillary morphology model of porous medium: straight parallel pores (tubes) each
having its own flow regime (generally the three types possible - the laminar, the turbulent and the
intermediate one)
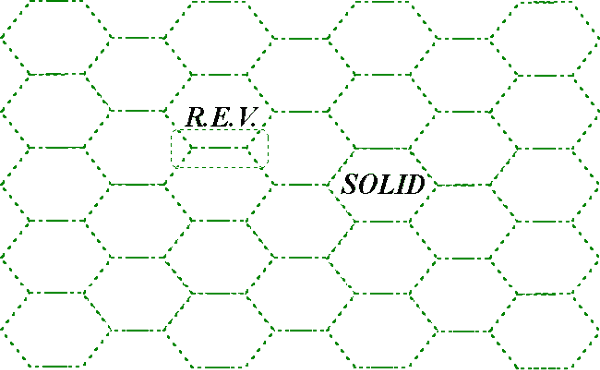
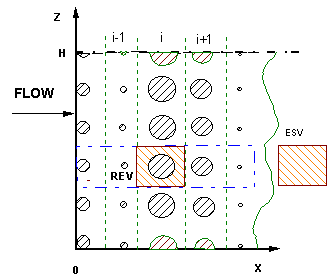
Figure 1a. Regular hexagonal 2-D capillary lattice morphology
Figure 1b. R.E.W.s for 2-D regular capillary morphologies: (a) hexagonal lattice, and (b) rhombic lattice
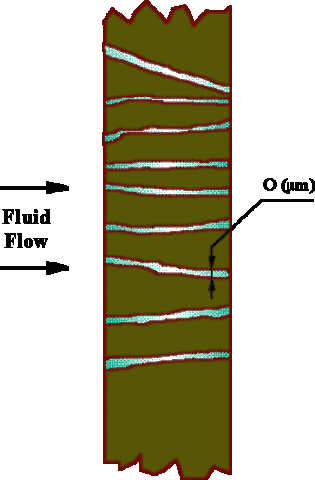
Figure 1c. Membrane schematic illustration
There are some general observations have been made regarding the range of regimes in porous media flow -
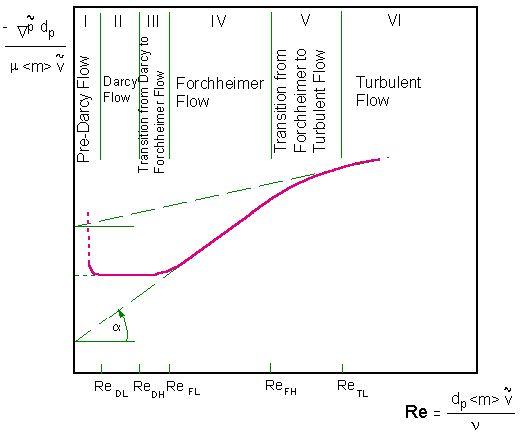
Figure 1d. Approximate zones of flow regimes in porous media (Modified after Fand et al.1987)
The simplest capillary morphologies are the following -
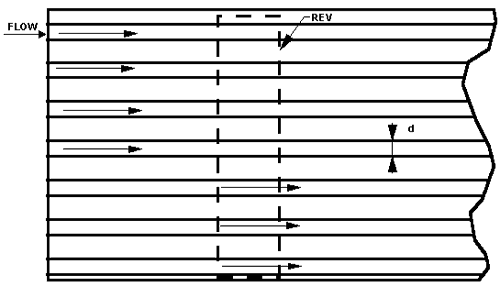
Figure 2a. Capillary morphology model of porous medium: a bundle of parallel tubes, all of the same diameter d, embedded in a solid
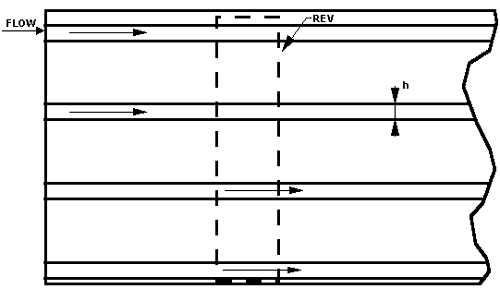
Figure 2b. Fissure closure morphology model: a bundle of parallel slits, all of width h, embedded in a solid
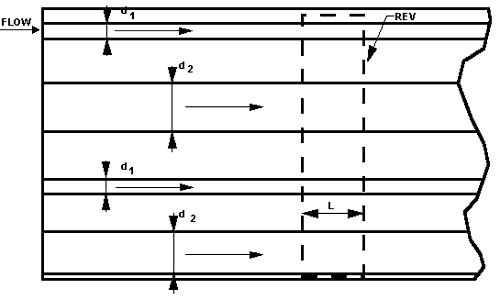
Figure 2c. A bundle of parallel tubes, with the indicated diameters d1 and d2, embedded in a solid. The ratio of the tube numbers with the diameter d1 to d2 is a significant concept in this morphological model
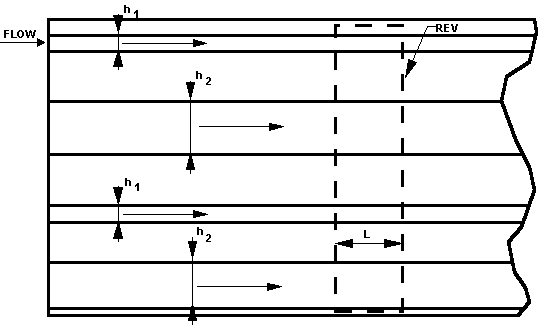
Figure 2d. A bundle of slits with two different heights (widths), h1 and h2
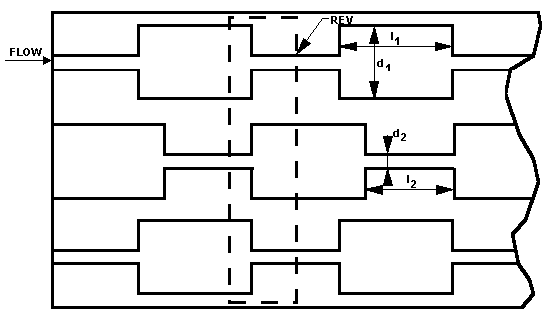
Figure 2e. A bundle of parallel tubes, with variable diameters for various parts of each. There are numerous statements related to the parameters d1, d2, I1, I2 and their respective distributions.

Figure 2f. A bundle of fissures, with variable width and length for various parts of each. There are numerous statements related to the parameters h1, h2, I1, I2 and their respective distributions.
As soon as the capillary models with the simple parallel arrangement of pores have been solved in the past for only linear laminar regime, the great principal interest for myself was to apply the HSP-VAT techniques for this problem - seeking the solution, which can at least be able to repeat the laminar regime solution, and at most being able to address the issue of existence of all three flow regimes in the each separate pore. It does that.
Here I would like to put aside the other motives, but one that I need to talk about more - because this is the first ever two-scale problem solved exactly in fluid mechanics and in physics, which has been solved actually analytically for the SPPM morphology with the three flow regimes in existence. This problem for two flow regimes - creeping and laminar, was stated throughout approximately from the XIXth century incorrectly when seeking the Upper scale bulk coefficient of pressure loss (friction factor). It was the following one published in -
with the following Figures accompanying the paper. Capillary morphology model of porous medium: a bundle of parallel pores embedded in solid
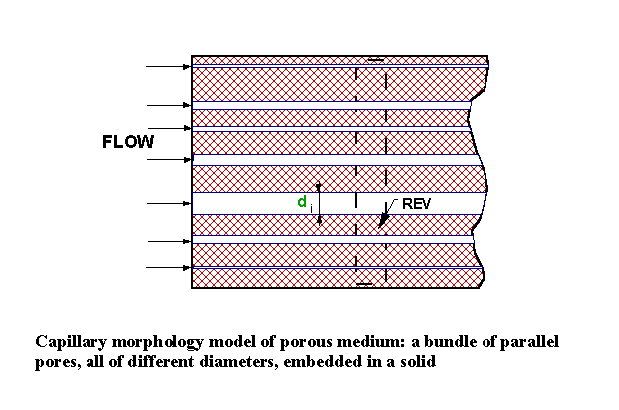
Figure 1.A Straight Parallel Pores Morphology (SPPM) porous medium
The VAT decomposition of the averaged variables and their presentations in the simple morphology of the two diameter pores leads to the following picture
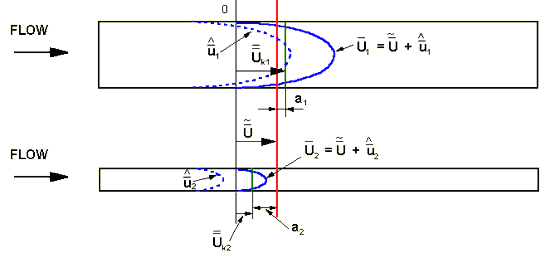
Figure 2. Momentum bulk and local evaluation in the two pores as an example of VAT description of Averaged and Local Variables in the straight pore parallel capillary morphology model (SPPM) of porous medium
The calculation of bulk (averaged actually) resistance in the medium shows that the morphology greatly effects this value (well, as everyone expected)
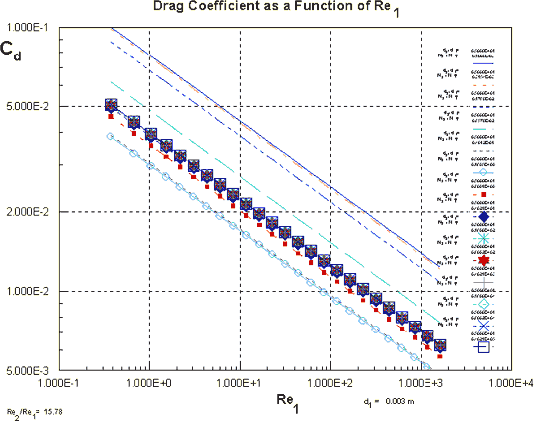
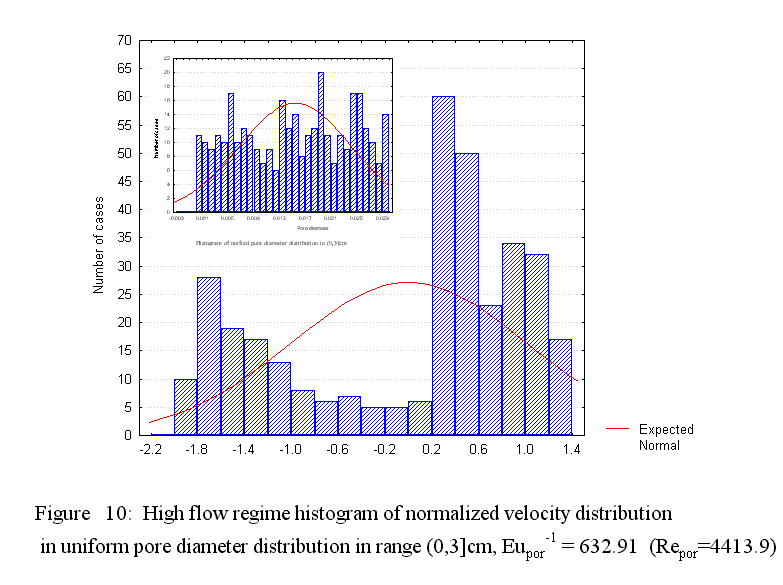
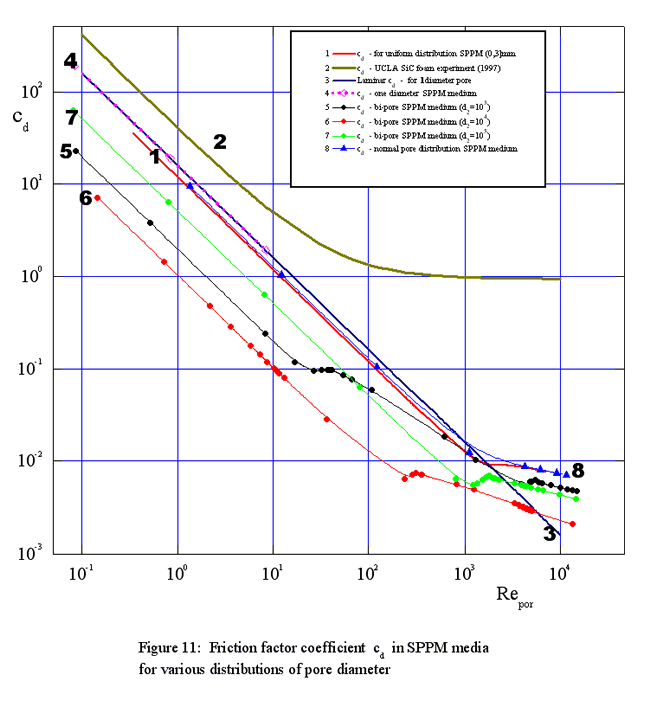
Figure 3a. Drag Coefficient as a Function of Re1 where the medium resistance can have strange irregularities due to change of flow regime within the pores
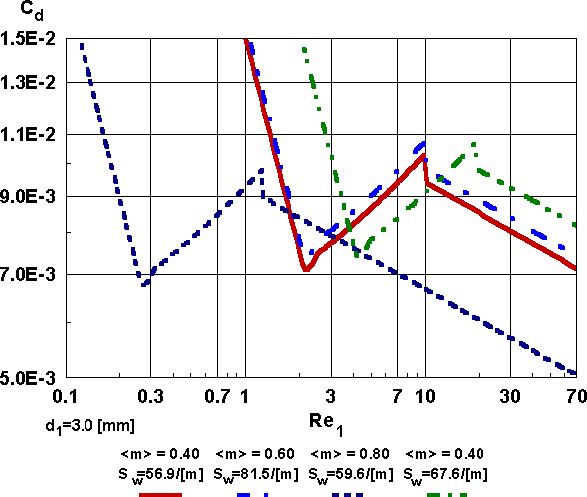
Figure 3b. The overall drag coefficient as a function of small pore Reynolds number for the straight capillary morphology
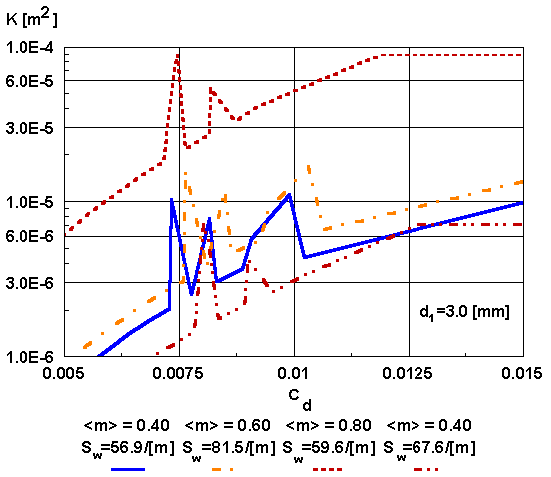
Figure 3c. The bulk permeability as a function of overall drag coefficient for the straight capillary morphology
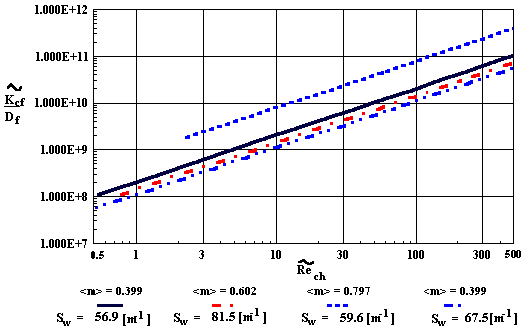
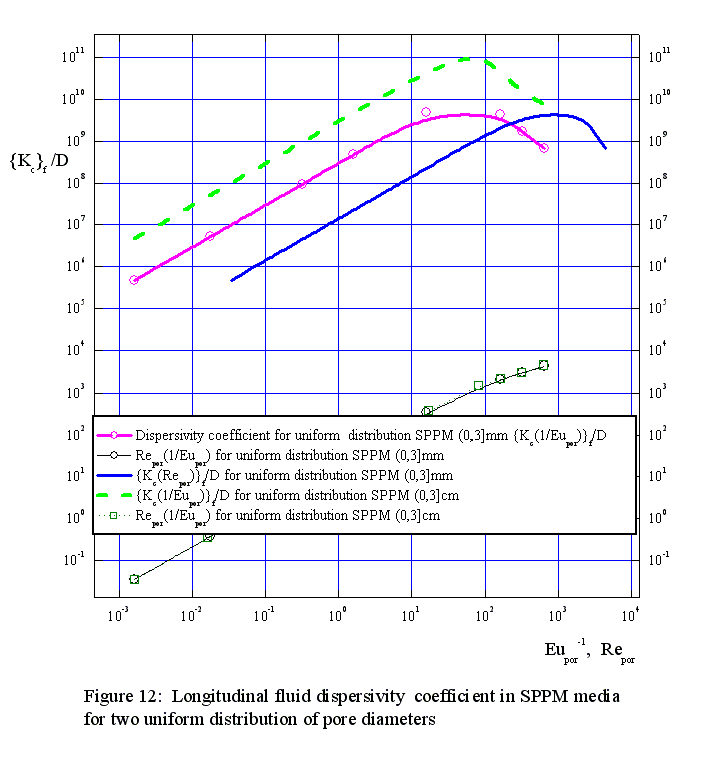
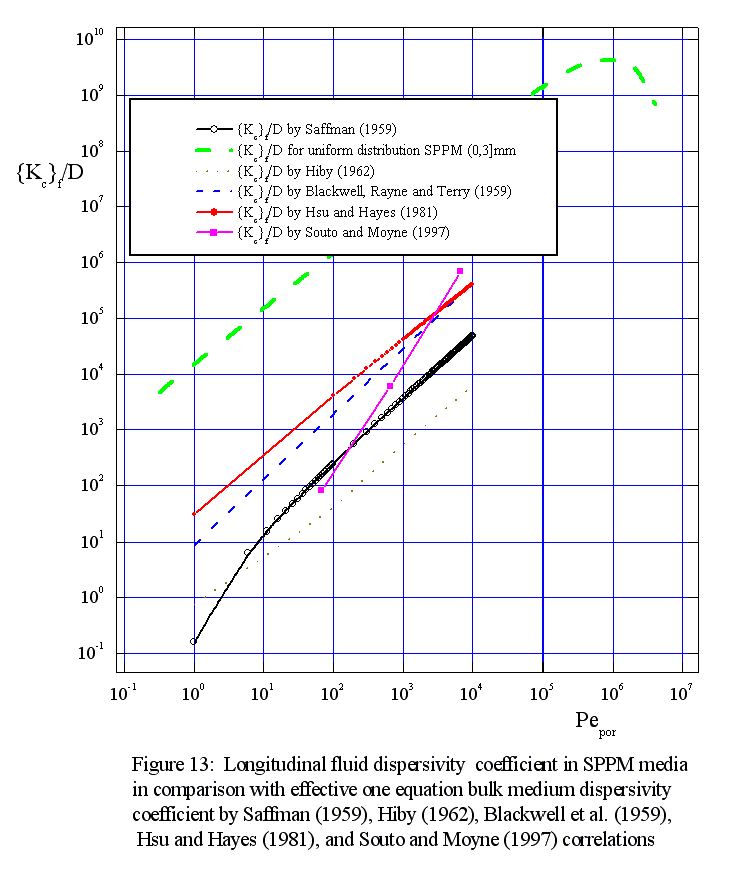
Figure 3d. Dimensionless longitudinal diffusion coefficient as a function of bulk Reynolds number for the capillary morphology
The momentum fluctuation values observed as of having a great dependency on diameters ratio -
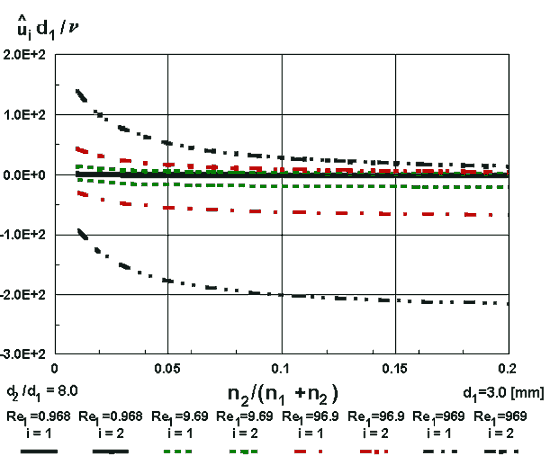
Figure 3e. Velocity fluctuation values over increasing large-pore number density for the straight capillary morphology and small diameter-ratio
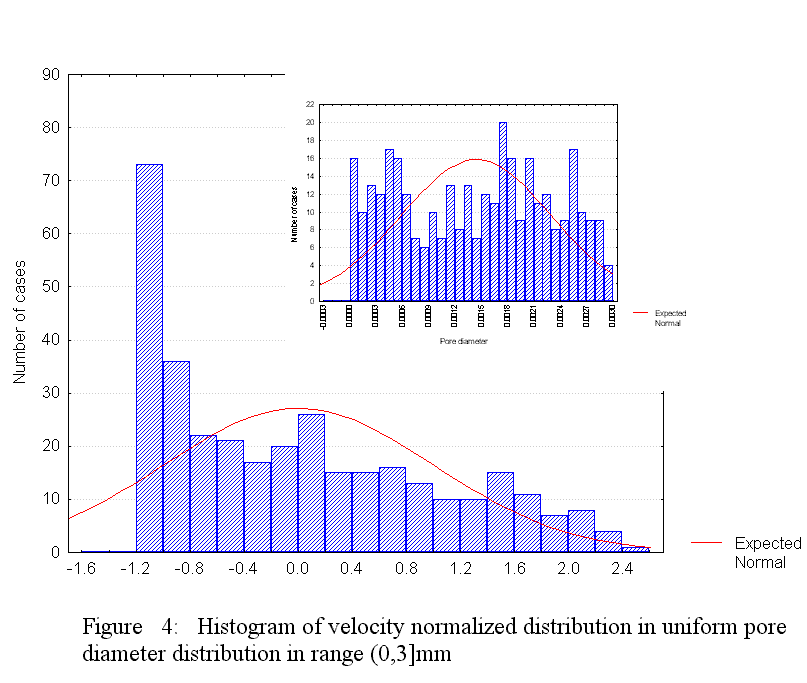
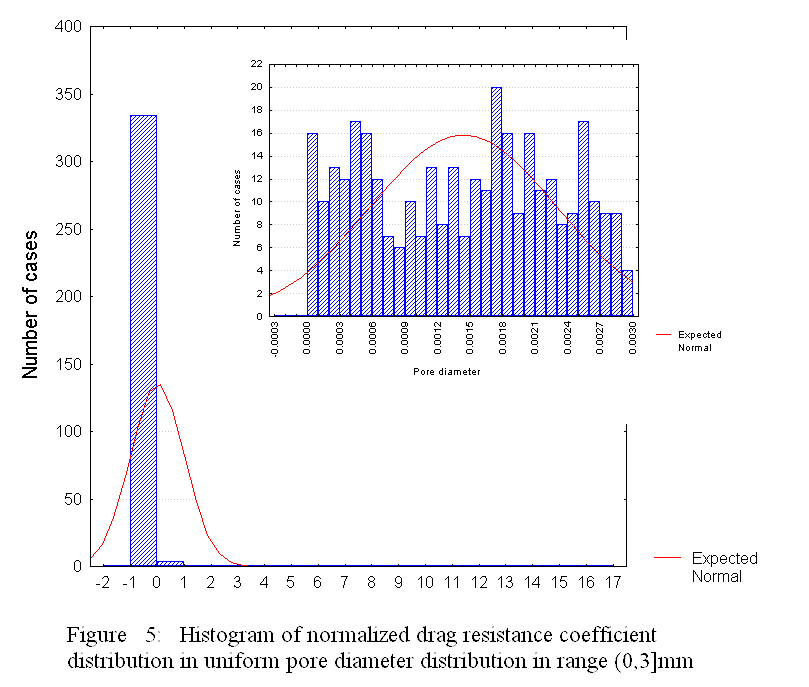
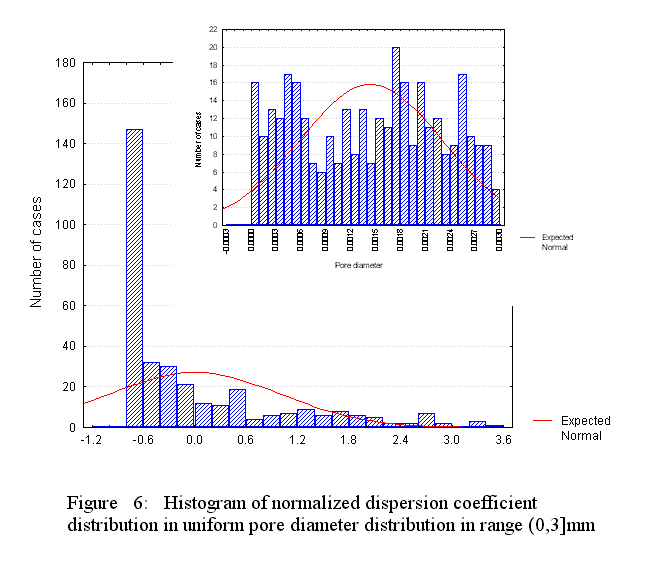
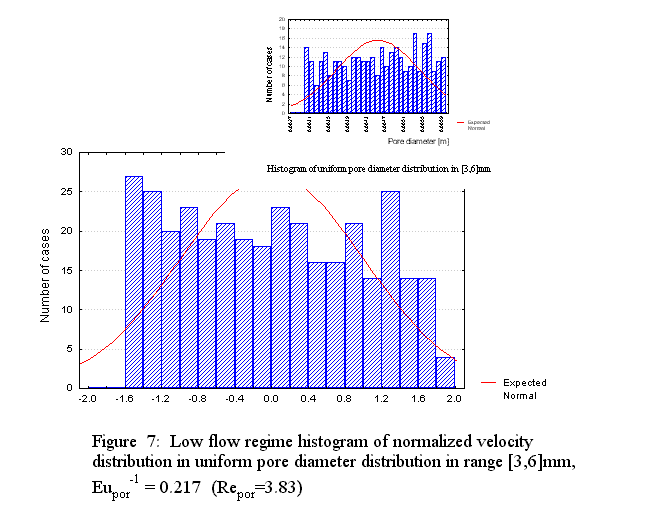
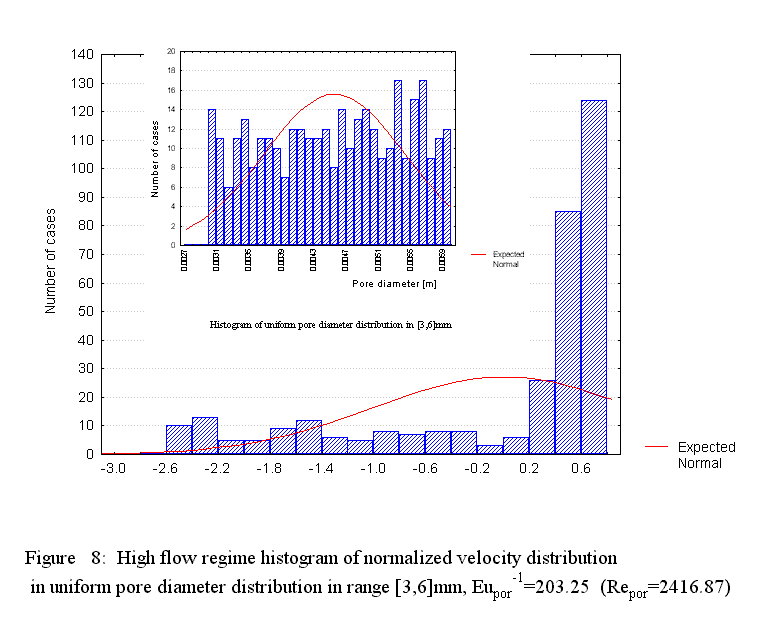
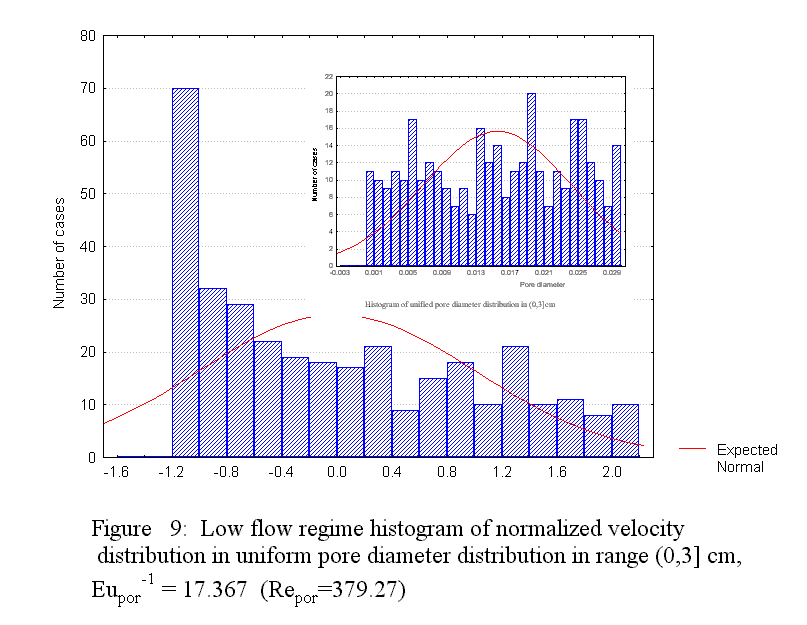
Description of the events occurring in a porous medium consisting of globular medium morphologies undergoing thermal and inertial phenomena can be done with the same HSP-VAT governing equations. The difference, meanwhile, would be in closure methods due to morphology. Treating a mechanical mixture with the upper scale HSP-VAT models can be provided when using the exact closure of additional terms or with the effective transport coefficients. Selection of effective transport coefficient models appropriate to the accepted morphology under study is most relevant under such treatment. Hence, "appropriate selection" is dictated by the matrix microstructure, which greatly influences both the transport coefficient magnitudes and spatial behavior of transport parameters.
Morphologies Description
Three packing with distinct characteristics are good models for globular morphology considered:
Regular packing of solid spheres with assigned morphology characteristics –

Highly porous medium consisting of disperse spheres with inter-spherical spacing
greater then 5 sphere diameters
Randomized series of spherical bead screens – 1-D globular morphology
Simple cubic unit cell structure with solid spheres at the lattice nodes and exact expressions
for the morphology functions –
Schematic of a regular bed with spherical packing and expected morphology function behavior
Bi-porous structure (depiction of a representative capillary) in –
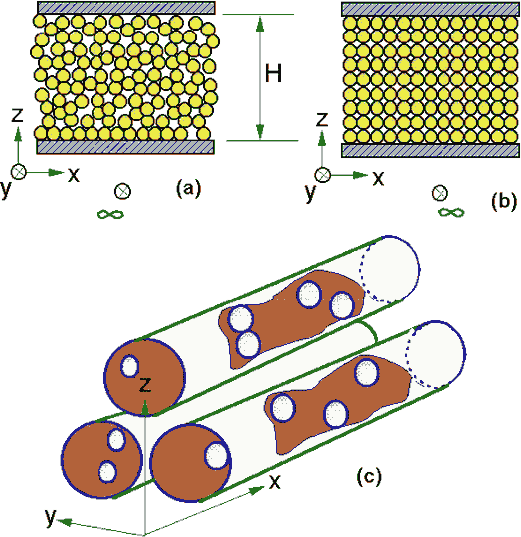
Schematic representations of varying morphologies: (a) regular, unspecified sphere packing with stationary destruction, (b) simple cubic periodic sphere packing, and, (c) bi-porous capillary morphology with internal obstructions
as well as another geometrical arrangements of globulars
Random Homogeneous Globular Morphology of Spherical Beads in 2-D Packed Layer

Space models consist of (a) regular and (b) irregular packings
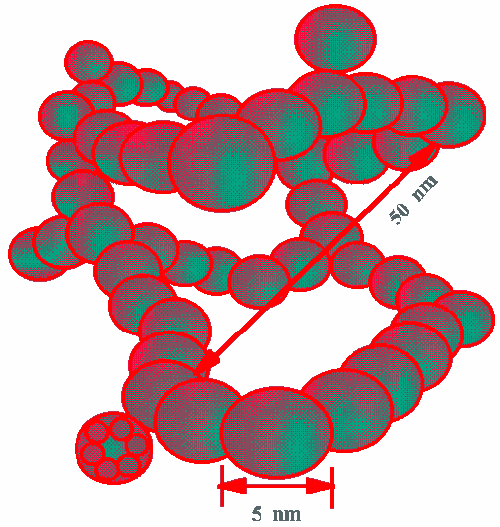
Aerogel ceramic morphology with high porosity
Rigorous descriptions of the morphologies employed for the three structures are offered
in Gratton et al. (1993, 1996).
THE INFLUENCE OF MORPHOLOGY UPON TWO-TEMPERATURE STATEMENTS FOR CONVECTIVE
TRANSPORT IN POROUS MEDIA (516K)
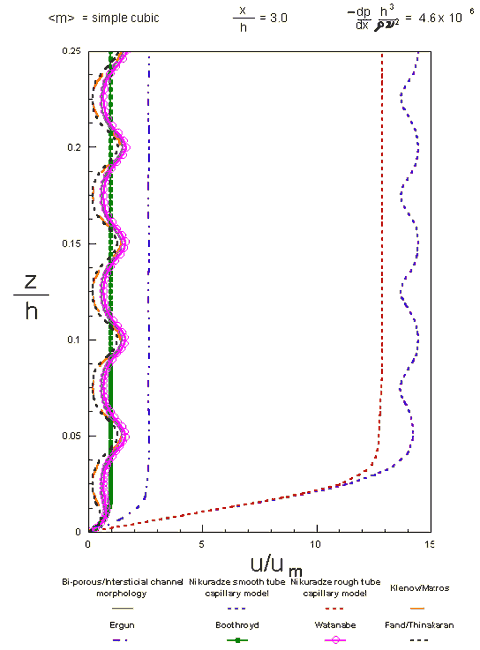
Velocity profile for simple cubic periodic morphology
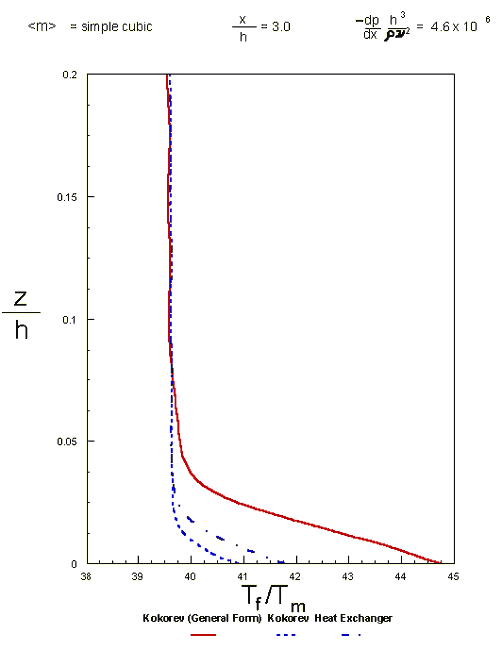
Fluid temperature profile for the simple cubic oscillatory morphology (2-temperature model)
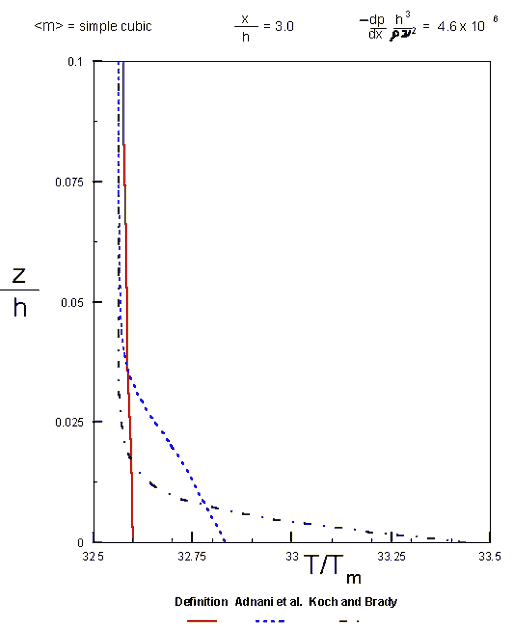
One - temperature profiles for the simple cubic oscillatory morphology
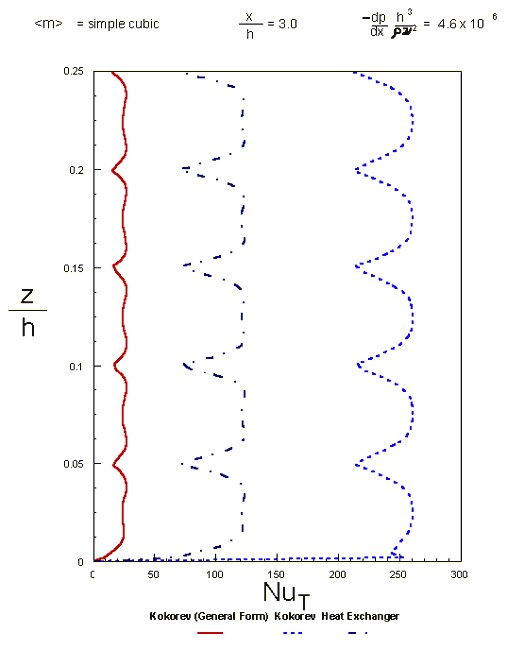
Turbulent Nusselt number profiles for the simple cubic oscillatory morphology
The porous or roughness layer (RL) is the layer between the subsurface and a similar surface running close to the roughness peaks, which is approximately parallel to the subsurface. The structural properties of the roughness layer (obstacle layer) were classified as regular, uniformly rough, non-uniformly rough, randomly rough and highly porous.
A WAT approach was used to develop turbulent flow and heat transport models on the primary level of the hierarchy - on the pore level. It had been shown that the flow resistance and heat transfer in a rough channel or pipe, as well as a fully occupied medium, can be properly predicted using the technique of averaging the transport equations over the REV. Random characteristics of the porous medium were simulated by the use of regular and unspecified statistical, pre-assigned solid phase morphologies.
An overall coefficient of drag resistance was determined by implementing a multiple-regime superposition approach. The superposition approach was tested for the case of a rough channel with included spherical obstructions. Coefficient models were evaluated using the governing averaged transport equations set and solved numerically. The transport model and the similarity assumptions were verified with smooth wall calculations by showing that the computed friction factors and velocity profiles have excellent agreement with commonly accepted correlations.
Reasonable predictions of friction factors for tubes roughened by rectangular and semi-circular ribs were made with the proposed drag resistance model for two-dimensional ribs that is based mainly on the effect of the local flow deflection in front of the rib. Insufficient experimental data were available for the verification of other geometries (triangular, trapezoid). It is postulated that the predictions for these geometries are also reasonable because the model worked well for "extreme" geometries (rectangular and semi-circular).
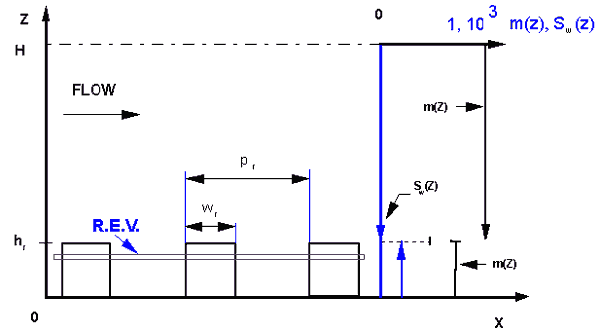
Two dimensional rectangular rib type roughness model
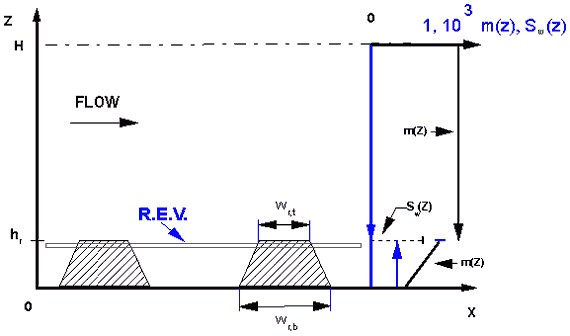
Two dimensional trapezoidal rib type roughness model
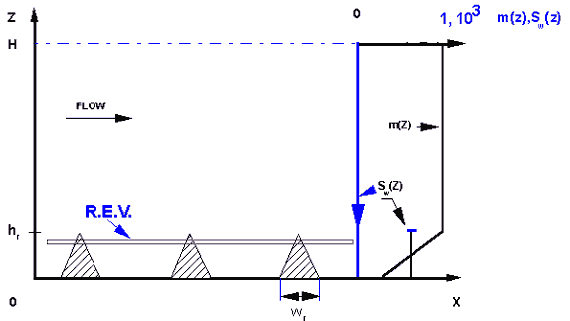
Two dimensional triangular rib type roughness model
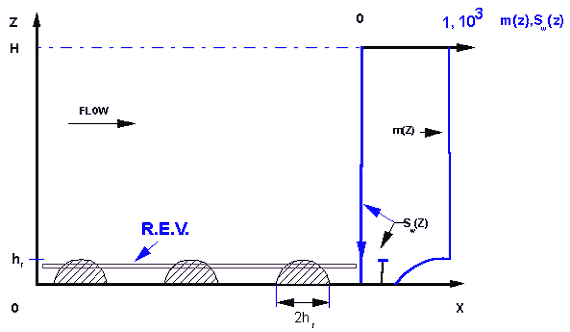
Two dimensional half-cylindrical rib type roughness model
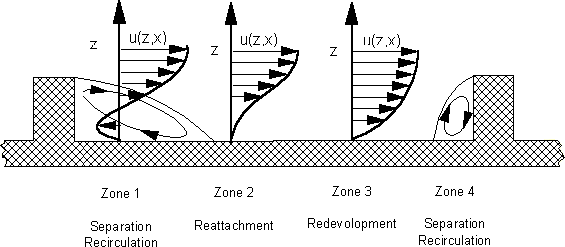
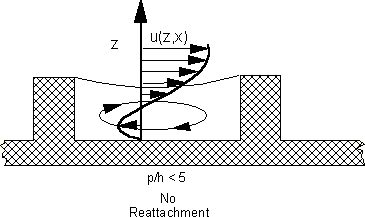
Flow between ribs with different pitch to height ratios
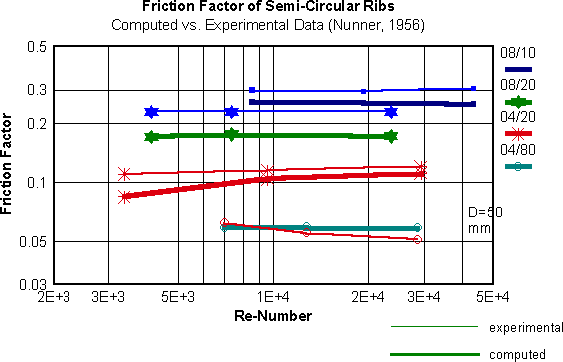
Computed vs/ experimental friction factor two -dimensional rib
Notation: 02/10 means h/D=0.02 and p/h=10/ All values are based on the pipe diameter D and are calculated in a flat channel with H-0.5 D
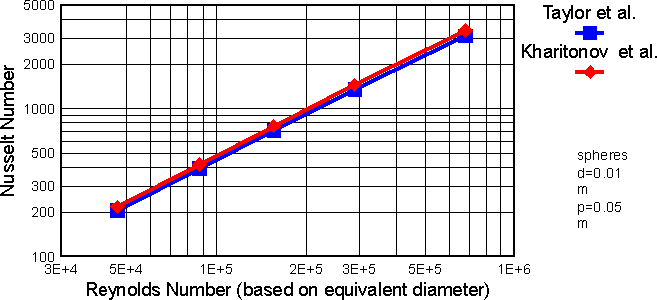
Comparison of Nusselt Numbers Calculated from Heat Transfer. Models of Taylor et al. Kharitonov et al. (all dimensionless values based on the pipe-equivalent diameter of the flat channel D=0.4 m)
The full scale mathematical problem statement is described in the subsection -
where this problem is stated and solved as the momentum-heat transfer problem with the validation purpose and with intension to look for the point whether the concept of the VAT methodology applied toward the rough channels would be technically more accurate and explanatory then the artificial simple models of 30-th of the last century.
Copyright © 2001 - 2017 V.S.Travkin, Hierarchical Scaled Physics and Technologies™