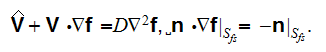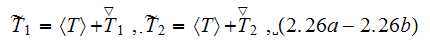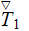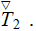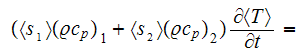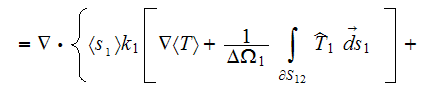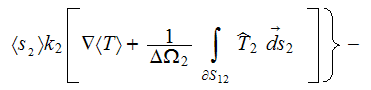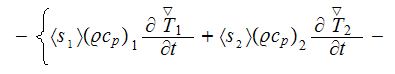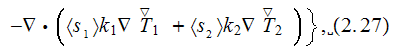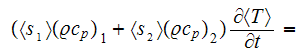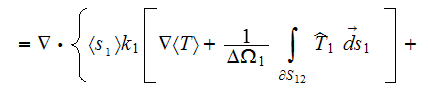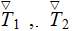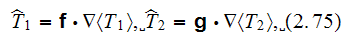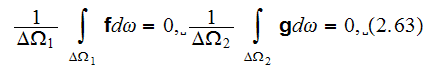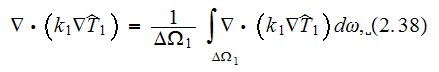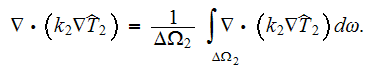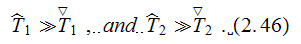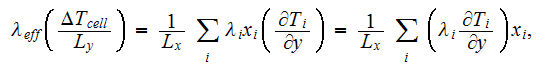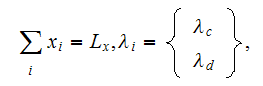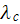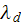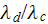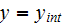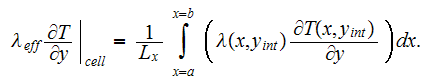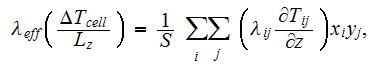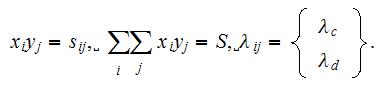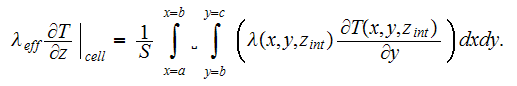Effective Coefficients in Thermal Physics
This is the great topic of tremendous importance. It was spoken about through the volumes.
One thing is obvious, when effective coefficients problem is razed for assessment in
a heterogeneous medium. And this is - because the effective coefficients search is the
problem of the Upper scale medium consideration, there is no other way to go around
the VAT governing equations for formulation the effective coefficient models
EFFECTIVE DIFFUSIVE TRANSPORT COEFFICIENT MODELING ( 88K)
Exact Closure Procedures of Hierarchical VAT
Capillary Thermo-Convective Problem for Turbulent and Laminar Regimes (589K)
Heat Transfer-pgs61-75 (1.0M)
Heat Transfer-pgs76-111 ()
HEAT AND CHARGE CONDUCTIVITIES IN
SUPERLATTICES - TWO-SCALE MEASURING AND MODELING (468K)
Few more remarks on correctness of the definition for "effective coefficient" can be found in the discussion
Discussion: "Alternative Models of Turbulence in a Porous
Medium, and Related Matters"( 70K)
which was driven by recent publications and by my desire to speak more on importance of not to profane some principal
definitions.
There are hundreds of papers on effective characteristics evaluation that we
could use as examples of - HOW NOT TO DO, What is incorrect in the homogeneous
"effective" coefficients determinations.
Unfortunately, the most frustrating feature of the paper by Eidsath et al.
(1983) is that the founder of scaled averaging technique and theories for few
disciplines (S.Whitaker) did not found other way to compare characteristics of
the VAT with the homogeneous characteristics of the lower scale problem
statement but as to follow the same lower scale physics procedures for
calculation of the such "effective" coefficients.
Of course, following this approach at that time they got to the same range of
outcome results as in others published homogeneous treatment of Heterogeneous
problems.
The closure was stated as for functions

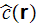 that is the fluctuation of the concentration field and for the dispersion
tensor
that is the fluctuation of the concentration field and for the dispersion
tensor

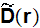 in the fluid phase determined as in our notations
in the fluid phase determined as in our notations
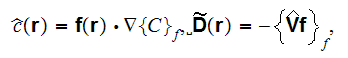
where the mathematical statement for

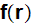 was taken (we read in the page 1809) as for
was taken (we read in the page 1809) as for
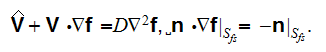
The solution of this closure problem was sought as for the problem's geometry
which used in all homogeneous statements for this kind of tasks
Here the numerical method and simulation procedure were made as for the GO
Theorem (GOT) - the homogeneous physics analysis and assessments, in spite
that the whole problem was stated and supposed to be solved as for the Upper
scale and according to the heterogeneous WSAM Theorem idea!?
What to say now ?
The outcome could be predicted.
So - everybody did ask at that time and continue asking now - For what
reasons we need to use these complicated, integro-differential, not affordable
mathematical non-local averaged statements (governing equations) for the
solution of our problems if the effective characteristics - those mostly we
are looking after, are actually the same as with the traditional statements!!
Really - for what reason?
That was a terrible, misleading mistake done by authors of this paper, as well
as by others in the same style.
Because these Effective coefficients are DIFFERENT. Well, sometimes, when the
problem is linear (constant coefficients) and we look for overall composite's
effective coefficients - then these effective coefficients - Heterogeneous
Media Effective and Homogeneous media presentation effective can be equal, as
to one can see in the first pure analytical Two Scale HSP--VAT solution for
the most tought and used diffusion, conductivity problem -
Meanwhile, if we are looking for separate, each phase effective coefficients,
and for the components of these effective coefficients, as in the case of High
Temperature Superconductors (HTSC), for example, and for the effective
coefficients in the very most of the problems in heterogeneous media, then
we need to use the correct mathematics and numerical procedures of the
HSP-VAT, see these features in the known problem example again in -
Thus, there is no need to return to the homogeneous media methods and
algorithms. This is incorrect. Look at our elaborative studies with the exact
solutions of Local and Heterogeneous Non-Local the same almost globular medium
problems on the Both scales in the subsection on Electrostatics -
The Fluxes (Displacement fields) are equal for some steady-state statements, yes, but not the effective
coefficients.
Reading on fundamentals of such things as closure and calculation of effective
coefficients presented, for example, by Quintard (1998) at the 11th Int. Conf.
on Heat Transfer, one might find in the page 280 the algorithm for computation of
this kind "homogeneous--like" effective coefficients:
"- take the average of the pore-scale equations;
- express the pore-scale equations in terms of temperature deviations;
- seek an approximate solution of the system of coupled equations, i.e., the
pore-scale and averaged equations. This is obtained through a representation
of the temperature deviations in terms of the macroscopic quantities such as
averaged temperatures, their gradients, ....;
- introduce these representations into the averaged equations to get the
macroscopic equations in a closed form involving only averaged temperatures.
This also provides an explicit link between the macroscopic effective
properties and the pore-scale characteristics.
It can be said that almost all in this program is correct. But the proverb
says - " the devil is in details."
In another work-study an accepting of the idea that the phase temperature
variables in each of the subvolumes

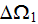 and
and

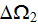 can be presented as sums of overall averaged temperature and local
fluctuations (Nozad et al., 1985)
can be presented as sums of overall averaged temperature and local
fluctuations (Nozad et al., 1985)
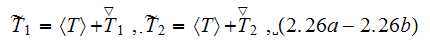
is not frustrating due to introduction of the two new variables

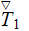 and
and

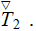 This can bring the the equation for the composite medium temperature follows
(Nozad et al., 1985) to the following definition
This can bring the the equation for the composite medium temperature follows
(Nozad et al., 1985) to the following definition
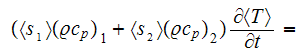
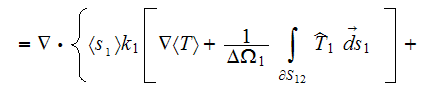
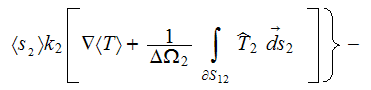
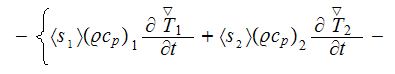
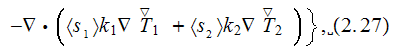
which has five (5) variable temperatures. If later on all the assumptions and
constraints given in Nozad et al. (1985) all satisfied then the final equation
with the only 3 different temperatures resumes
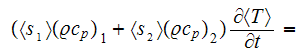
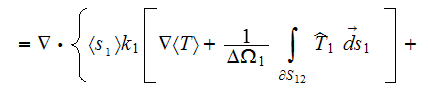
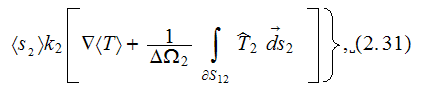
which means that the neglect of global deviations

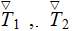 terms
still not removes the requirement or the two temperature solution.
terms
still not removes the requirement or the two temperature solution.
Closure of Multiple Temperature Equations Problem used in the study.
One of the first closure procedures were developed by Whitaker and co-authors
(see, for example, Nozad et. al., 1985)
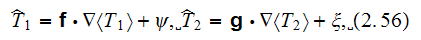
those later on were accepted as
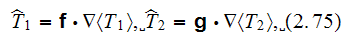
also there is need for requirement
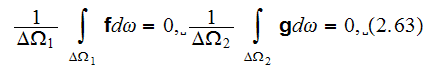
The closure equations for fluctuations functions - see in the page 847 are
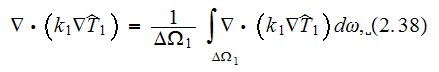
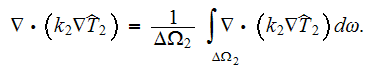
A number of accepted assumption make possible to write the fluctuation closure
equations in this simplified form. Important among them are
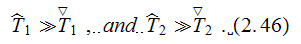
The fluctuation closure variables found to be evaluated through the solution
of the problem
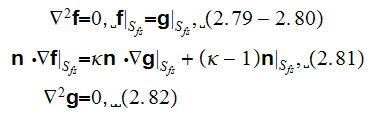
where the mathematical solution (p.849) with the note - "It should be clear at
this point that the closure problem is nearly as complex as the original
problem stated by eqns. (2.1) - (2.6); however we have no intention of solving
for

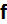 and
and

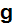 over the macroscopic region. Instead we want to solve for
over the macroscopic region. Instead we want to solve for

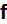 and
and

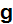 in some representative region and use the results to predict the effective
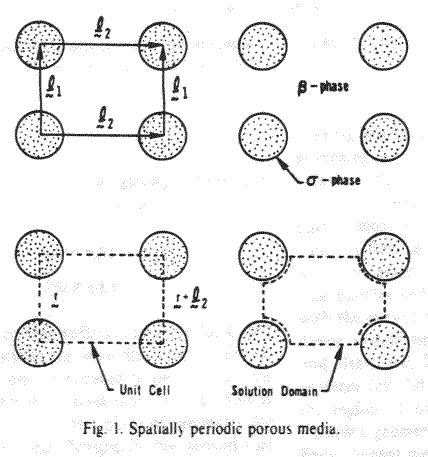
thermal conductivity for that region. Such a representative region is
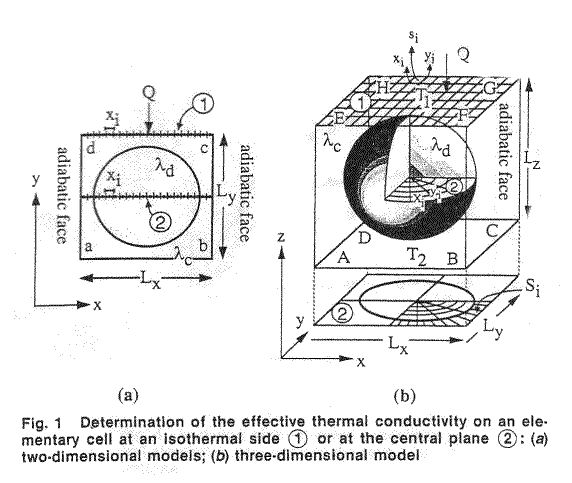
illustrated in Fig. 2 "
in some representative region and use the results to predict the effective
thermal conductivity for that region. Such a representative region is
illustrated in Fig. 2 "
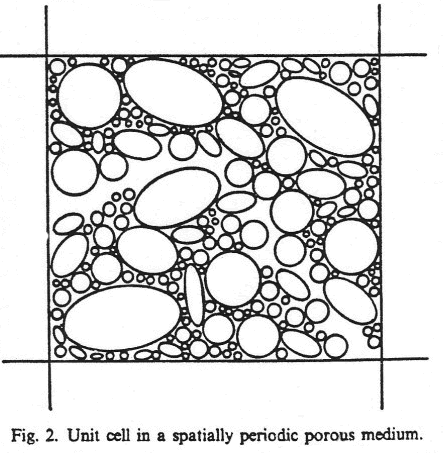
The figure is done as for the one phase intersected by the REV's boundary
surface, and the same is done in the Fig. 3 page 850. They compared these
homogeneous assessments for the heterogeneous problem with the same kind of
Homogeneous experiments in the Fig. 6, page 853.
We did analysis of this common for the technology, science, and industry
mistake for presentation of effective assessments and coefficients for
heterogeneous media, see in -
We need to say again - that in this paper the GO Theorem (GOT) - and the
homogeneous physics analysis and assessments were used in the Heterogeneous
problem and instead of the Upper Scale treatment was used the Lower Scale
treatment! With the predictable outcome.
By this mathematics alone and by that REV in Figs. 2,3 on p. 849 and p.850,
authors of the paper deadly hurt the great idea of importance and difference
of the effective coefficients for the Upper scale VAT statement and physics.
Because they presented them as of no big difference (or equal) as to the
conventionally calculated homogeneous "effective" coefficients!? It seems,
they did afraid to be different.
The usual procedure for experimental
measurement of effective coefficient of thermal conductivity we can find in
the paper by Orain et al. (2001). For the three scale medium - as in their
Fig. 1, they used the just homogeneous technique we spoke few times in our
texts.
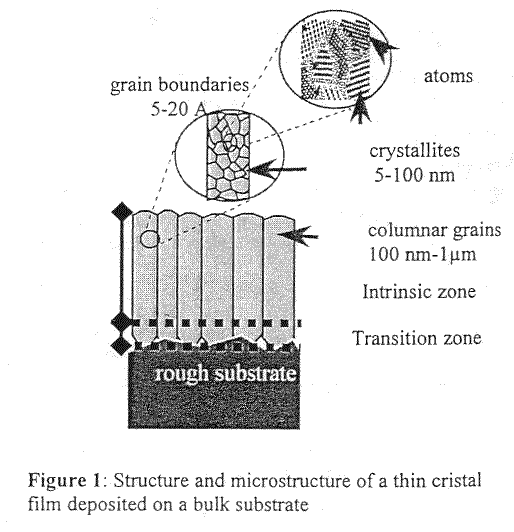
As we read in the page 256: "A thermal conductivity measurement method was
developed for the thermal characterization of submicron dielectric thin films
[3]. The technique, based on analysis of the transient temperature response
induced by a laser pulse, uses a thin gold electrical resistance (#150 nm) as
a temperature sensor deposited on the dielectric material.
The thermal conductivity is identified, simultaneously with a thermal boundary
resistance between the sensor and the film, by fitting experimental and
theoretical responses with a genetic algorithm [4]. "
That can mean ONLY that the Homogeneous GOT (theorem) helped to
determine the "effective" transient "bulk" coefficient of conductivity in this
study. But not the Effective Multiscaled Heterogeneous Coefficient of
Conductivity as they want for their products - silicone and zirconia oxides,
polymeric films. No surprise that in every industry and every company doing
these measurements for themselves again and again. Then getting those
coefficient tables as the internal trade secret - still the wrong data.
In their numerical experimental study Veyret et al. (1993) used to calculate
the 2D effective coefficient in globular morphology composite as, for example,
for 2D arrangements with cylindrical discontinuous phases using the formula
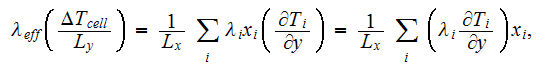
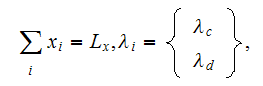
where

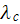 and
and

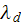 are the conductivity coefficients in continuous and discontinuous phases.
are the conductivity coefficients in continuous and discontinuous phases.
From page 867 we read: "The calculation is carried out in a plane parallel to
the isothermal boundaries. Figure 4 shows the effective thermal conductivity
variations for square-in-square and circle-in-square systems for different
conductivity ratio

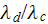 and concentration. "
and concentration. "
We need to understand by this - that there was the 1D, integration of the flux
over the line

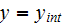 as
as
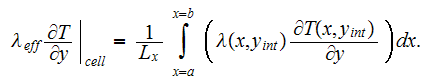
So, obviously it is not the averaged over the composite volume dependency for
the heat transfer flux. Yes, in this problem the integration over the plane
surface parallel to the isothermal boundaries gives the same heat flux as
needed for energy conservation. But this is not the Effective Volumetrically
averaged heat flux and effective coefficient, and this neither correct
averaging nor correct VAT heterogeneous averaging.
Also - the very important point is - That these boundary conditions were the
setup for the one cell, they are not representing the real BC for the cell in
the composite medium.
The 3d like methodology for calculation of "effective" coefficient by Veyret
et al. (1993) were based on the same idea
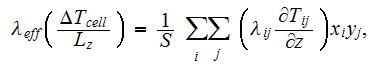
where surface of the
(
 )
element, and the surface of the horizontal cross-section of the cell
)
element, and the surface of the horizontal cross-section of the cell

 are
are
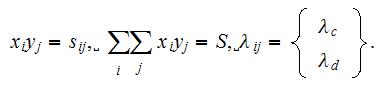
In continuous formulation this formula means
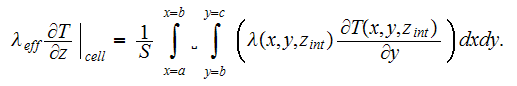
That means again no close match by the definition to the proclaimed
volumetrically averaged "effective" coefficient, not talking about the
heterogeneous Upper scale effective coefficient of conductivity for the 3d
globular medium.
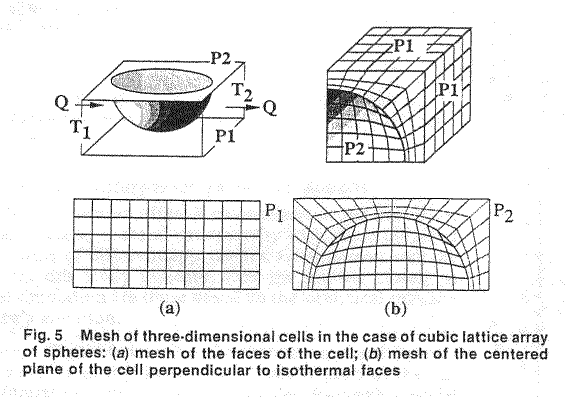
The general usage of homogeneous formulae based on the homogeneous GO theorem
for numerical, physical experiment and theoretical procedures give not
surprisingly the close, reasonably close curves for such "effective"
coefficents, see in this paper figures as
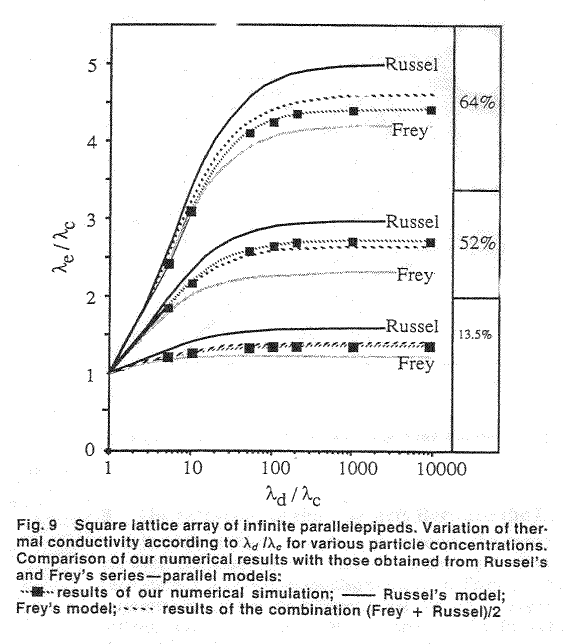
That is why all the body of these results is from the same flock - we are
saying that the "birds of a feather flock together". And there is nothing
offensive or insulting tone should be found in my these words.
People who read my studies, or my co-authors know that I am saying this for a
lot of years.
The problem is with the scientific and technological needs. They are of not
great demanding needs in most of the old established industries, so this kind
of homogeneous results satisfying all folks.
The only perhaps breakthrough in understanding and perception
happens when more and more "Columbia" kinds of disaster will force the
technological communities to re-estimate their basic grounds for
products.
Or, the some new technology won't getting into reality unless the new more
accurate tools will be used for their development and design. First of
all this should happen probably in the Nanotechnologies and in Biotech-Medicine -
Through the last more than ten years, mostly because I was affiliated with UCLA, I was careful when emphasized
my opinion and mathematics with regard of homogeneous "effective" coefficients for heterogeneous media. The common knowledge and use
coefficients. We published few works with the two scale VAT analysis of the problem, as those referred above and below,
but no strong message was sent?
Nowadays, especially when after 2002 the few more common textbooks known problems were solved
as they should be - on the two scales, see in -
there is the belief that then we serve to the good purpose stressing out following to the all above
information and proofs, as well as to the mathematical analysis in -
that
1) The all effective coefficients obtained for heterogeneous
media with mathematics based on the homogeneous GO theorem give incorrect
results!
The actions ought to be corresponding to this message.
References:
Eidsath, A., Carbonell, R.G., Whitaker, S., and Herrmann, L.R., "Dispersion in
Pulsed Systems - III. Comparison Between Theory and Experiments For Packed
Beds," Chemical Engineering Science, Vol.38, No. 11,
pp. 1803-1816, (1983).
Quintard, M., "Modelling Local Non-Equilibrium Heat Transfer in Porous Media,"
in Proc. 11th Intern. Conf. on Heat Transfer, Korea,
Vol. 1, pp. 279-285, (1998).
Nozad, I., Carbonell, R.G. and Whitaker, S., "Heat Conduction in Multiphase
Systems I: Theory and Experiment for Two-Phase Systems,"
Chem. Engnr. Sci., Vol.40, No. 5, pp. 843-855, (1985).
Orain, S., Scudeller, Y., and Brousse, T., "Investigation of Structural
Effects on Thin Film Thermal Conductivity," in 7th
International Workshop on Thermal Investigation of IC's and Sytems -
THERMINIC, Paris, Laboratoire TIMA, pp. 256-259, (2001).
Veyret, D., Cioulachtjian, S., Tadrist, L., and Pantaloni, J., "Effective
Thermal Conductivity of a Composite Material: A Numerical Approach,"
J. Heat Transfer, Vol. 115, pp. 866-871, (1993).
Travkin, V.S., "Discussion: "Alternative Models of Turbulence in a Porous
Medium, and Related Matters," (D.A. Nield, 2001, ASME J. Fluids Eng., 123, pp.
928-931)," J. Fluids Eng., 123, pp.
931-934, (2001).
Travkin, V.S. and Catton, I. Porous Media Transport Descriptions -
Non-Local, Linear and Non-linear Against Effective Thermal/Fluid
Properties//Advances in Colloid and Interface Science. 1998. V.76-77.
P.389-443.
Travkin, V.S. and Catton, I. Transport phenomena in heterogeneous media
based on volume averaging theory// Advances in Heat Transfer. (New York,
Academic Press, 2001. Vol. 34.). P.1-144.
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 7-17, (2005).
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005).
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005).
Copyright © 2001...Thursday, 03-Jul-2025 05:28:22 GMT V.S.Travkin, Hierarchical Scaled Physics and Technologies™

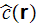 that is the fluctuation of the concentration field and for the dispersion
tensor
that is the fluctuation of the concentration field and for the dispersion
tensor

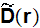 in the fluid phase determined as in our notations
in the fluid phase determined as in our notations
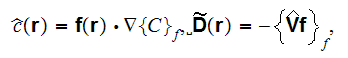

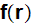 was taken (we read in the page 1809) as for
was taken (we read in the page 1809) as for