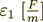 - dielectric permittivity of the odd layers,
- dielectric permittivity of the odd layers,
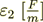 - dielectric permittivity of the even layers;
- dielectric permittivity of the even layers;
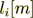 - thickness of i-th layer;
- thickness of i-th layer;
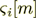 - coordinate of the boundary of the i-th layer;
- coordinate of the boundary of the i-th layer;
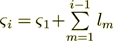 , where
, where 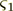 is the
layers pack's upper boundary z-coordinate.
is the
layers pack's upper boundary z-coordinate.
There is the system of k layers, layers are changing one after another
(intermitting); with 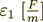 - dielectric permittivity of the odd layers,
- dielectric permittivity of the odd layers,
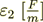 - dielectric permittivity of the even layers;
- dielectric permittivity of the even layers;
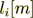 - thickness of i-th layer;
- thickness of i-th layer;
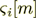 - coordinate of the boundary of the i-th layer;
- coordinate of the boundary of the i-th layer;
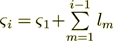 , where
, where 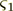 is the
layers pack's upper boundary z-coordinate.
is the
layers pack's upper boundary z-coordinate.
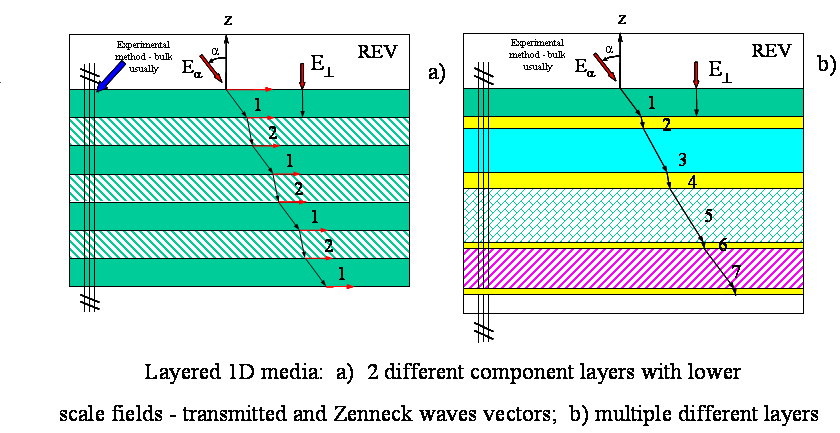
1) We consider the incidence of the TE type (s-polarized) wave
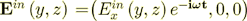 from the upper half-space (z>0) with the dielectric permittivity
from the upper half-space (z>0) with the dielectric permittivity
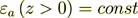 , onto the lower subspace
, onto the lower subspace 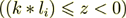 with the heterogeneous medium of 100 or 200 or even bigger number (600) of layers, consisting of homogeneous, with constant
coefficients layers of two kinds, or inhomogeneous layers of two kinds when each layer of each kind has the nonlinear dependency of
material's electric properties.
with the heterogeneous medium of 100 or 200 or even bigger number (600) of layers, consisting of homogeneous, with constant
coefficients layers of two kinds, or inhomogeneous layers of two kinds when each layer of each kind has the nonlinear dependency of
material's electric properties.
But the last case has the much more complicated solutions and equations.
So, at first we have to use the Helmholtz equation 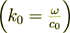 for the upper half-space region
for the upper half-space region
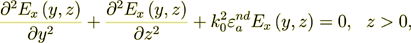 | (1) |
 | |
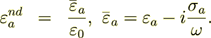 | |
where 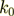 - the wave vector of the incident wave.
- the wave vector of the incident wave.
The same kind of traditional wave equation we use here for each layer.
1) First period - two layers -
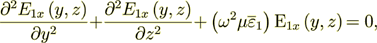 | (2) |
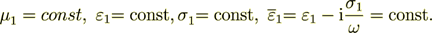 | |
and
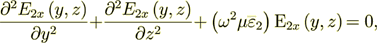 | (3) |
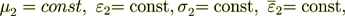 | |
with the conjugate boundary conditions of the IV-th kind BC's as like in thermophysics. The two fields are having in the interface surface the BC's, for example, when the phase 1 contacts with the phase 2, then for the tangential components of the electric field should be
 | (4) |
while the second BC appears from the condition for magnetic fields due to Amper's law
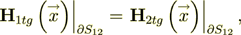 | (5) |
which implicates that
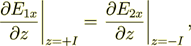 | |
where the subscript I means - the interface.
Because for the linear problem
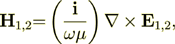 | (6) |
which, for example for 1D vertical wave propagation will be
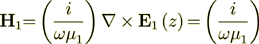
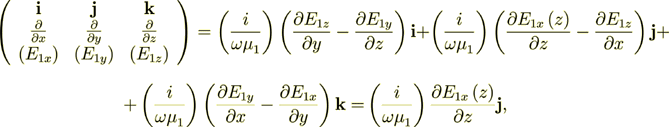 (7)
(7)so the BC we can write
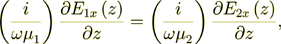 (8)
(8)and because we assumed here that 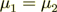 then
then
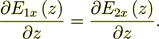 (9)
(9)For the 2D case we have - TE polarized in x-axis direction 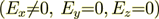
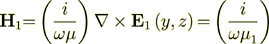
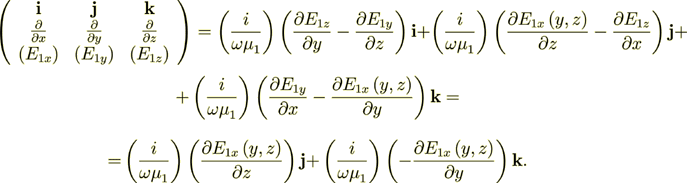 (10)
(10)So, anyway the tangential component 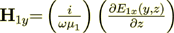 will lay on the
interface surface and the second BC will be the same.
will lay on the
interface surface and the second BC will be the same.
While for the bottom interface surface Ib of the 2 layers period we have the BC's
 (11)
(11)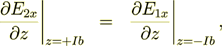 (12)
(12)connecting fields to the following period. And for the all other periods the same mathematical statements occur.
When conductivity coefficient  , then the VAT equation in phase one simplifies to
, then the VAT equation in phase one simplifies to
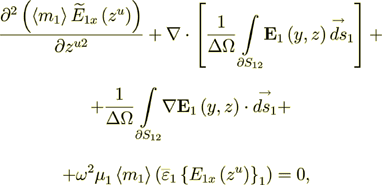 (13)
(13)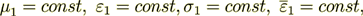
when we also have from the lower level 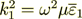 .
.
In the phase two the Upper scale governing equation is
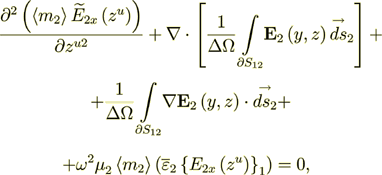 (14)
(14)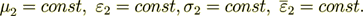
This problem is stated as for the data reduction or transmitting (communicating, linking) the data of solutions on both scales.
As we are saying in many places of this website - that the most interesting are the combined Upper scale phenomena, Non-Local characteristics, no matter how one names them or thinks to know what we are talking about. In spite that the problem could be solved exactly for the Lower scale physics as one of few solved so far we are talking in this subsection, the goal of this solution in all such complicated two, or more scale tasks is the finding characteristics of physical fields for the Upper (larger) scale physics.
Also, it is highly desirable to find out the ways, the possibility to connect fields in both directions of scaling - for conventional usually understood the "Bottom-Up" scaling as well as when the fields found in opposite direction - as for the "Top-Down" way of external fields applied. The latter way of directing of fields is even more often can be found in technological, natural problems.
We will talk later on the issues related to the "Top-Down" sequence of field's influence - and what does this mean for the mathematical statement and data interpretations.
We have found that this communication can be confirmed even in analytical form as that was discovered first for the electrostatics (and steady state heat conductivity) problem -
For solving this wave mechanics problem with the Four Governing Equation and the boundary conditions for the lower scale statement, few methods were used. One of them is the method fashioned by Zuev et el., (1989) where layered structure allowed to have periodical characteristics.
-Rep25.png)
Here the function B(z) is not the superlattice's morphology defining characteristic.
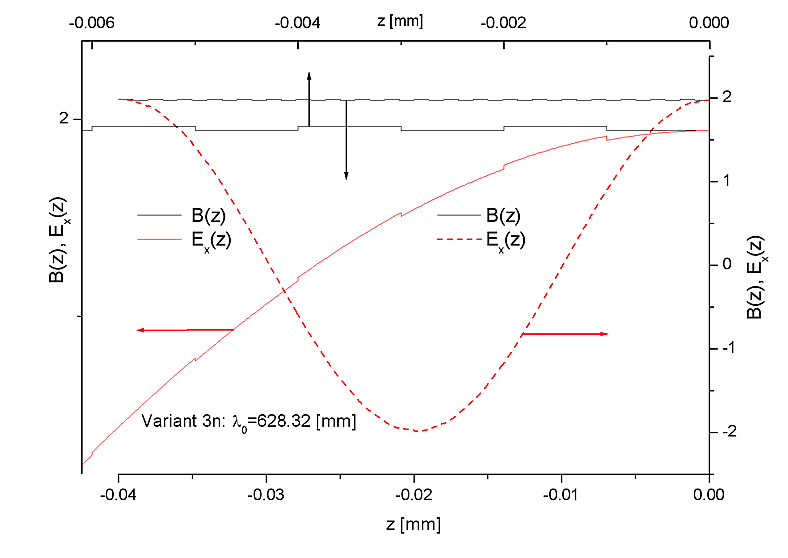
Long length wave EM field variations inside of the superlattice.
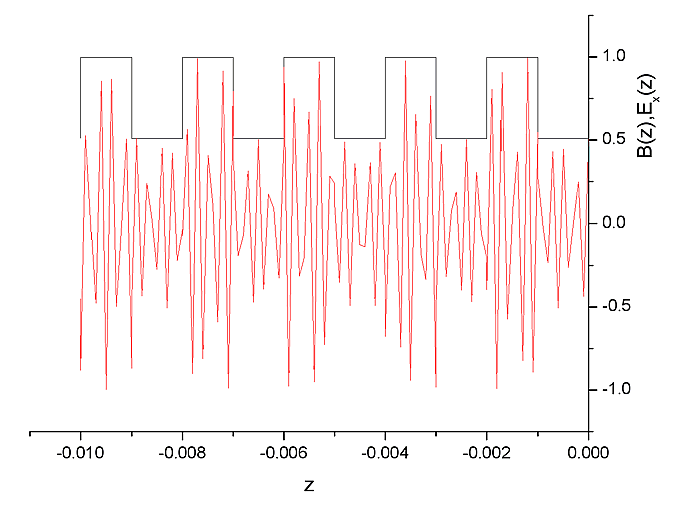
Electrical field functions in the superlattice when dielectric permittivity has the strong component change values.
-Rep24.png)
Each Phase Layers Short Wave Electrical Field Distibution.
-Rep24.png)
The Lower Scale Electric Field Derivatives Functions Used for Assessment of Transmitted Second Scale Wave Characteristics.
-Rep24.png)
Again as in the Ht Acoustics - as long as this is the fundamental decent problem, problem that communicates with and has impact for many technologies - so far with published by other authors results pertaining to only the lower scale local aspects of homogeneous EM waves propagation (no matter what authors saying), we continue to study some aspects of it and will be uploading data and interesting summaries for education and comparison with the homogeneous Electrodynamics results for this Exceptional problem.
Kondilis, A. and Tzanetakis, P., "Numerical Calculations on Optical Localization in Multilayer Structures with Random-Thickness Layers," Phys. Rev. B., Vol. 46, pp. 15426-15431, 1992.
Kondilis, A., "Combined Effect of Periodicity, Disorder, and Absorption on Wave Propagation Through Stratified Media: An Approximate Analytical Slution," Phys. Rev. B., Vol. 55, pp. 14214-14221, 1997.
Malyshkin, V., McGurn, A.R., Elson, J.M., and Tran, P., "Transverse or Off-axis Localization of Electromagnetic Waves in Random One- and Two-Dimensional Dielecric Systems Which are Periodic on Averaged," Waves in Random Media, Vol. 8, No. 2, pp. 203-228, 1998.
Sheng, P., White, P., Zhang, Z.Q., and Panaicolaou, Scattering and Localization of Classical Waves in Random Media, Ed. P.Sheng, World Scientific, Singapore, p. 563- ??
Mott, N.F. and Davis, E.A., Electronic Processes in Non-Crystalline Materials, Clarendon, Oxford, ch.2., 1971.
Bell, P.M., Pendry, J.B., Martin, M.L., and Ward, A.J., "A Program for Calculating Photonic Band Structures and Transmission Coefficients of Complex Structures," Comput. Phys. Commun., Vol. 85, pp.306-322, 1995.
Yeh, P., Optical Waves in Layered Media, Chichester, Wiley, 1988.
Zuev, M.A., Sisakyan, E.N., and Shvartsburg, A.B., "On the Structure of Waves Interaction in the Medium with Periodically Purturbed Characteristics," in Computer Optics, ICNTI-CDBU AN USR, 1989, No. 6, pp. 43-45 (in Russian).