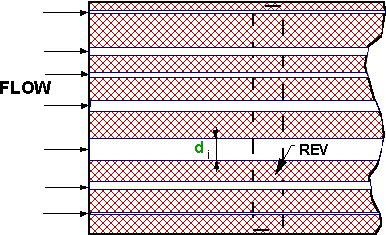
Fig. 1 Capillary morphology model of porous medium: a bundle of parallel pores embedded in solid
The Annals of Frontier and Exploratory Science
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany, Denver, CO, USA
There are two reasons why these problems demand a fundamental attention:
1) These classical problems (straight capillary, single diameter globular morphologies, and 1D layered systems) are already present examples of pure statements of the test-problem for more then hundred years. Few generations of researchers tried to solve these problems, but did not obtain a complete solution. Further, the conjugate problem of heat transport in capillary systems has neither been stated fully nor correctly. The studies referred to below are the solutions for both scales and directly explain how these problems can be treated using the general HSP-VAT governing equations.
2) To help those who are working in the field, or are just interested, obtain familiarity with the simplest multi-scale problems and give them an understanding how to correctly state the VAT problem and what are the possibilities to treat it.
Few fundamental features of treatment of these morphologies in fluid mechanics are given in - Fluid Mechanics::Classical Problems
The most simple and at the same time trustworthy morphology as we all used is

Fig. 1 Capillary morphology model of porous medium: a bundle of parallel pores embedded in solid
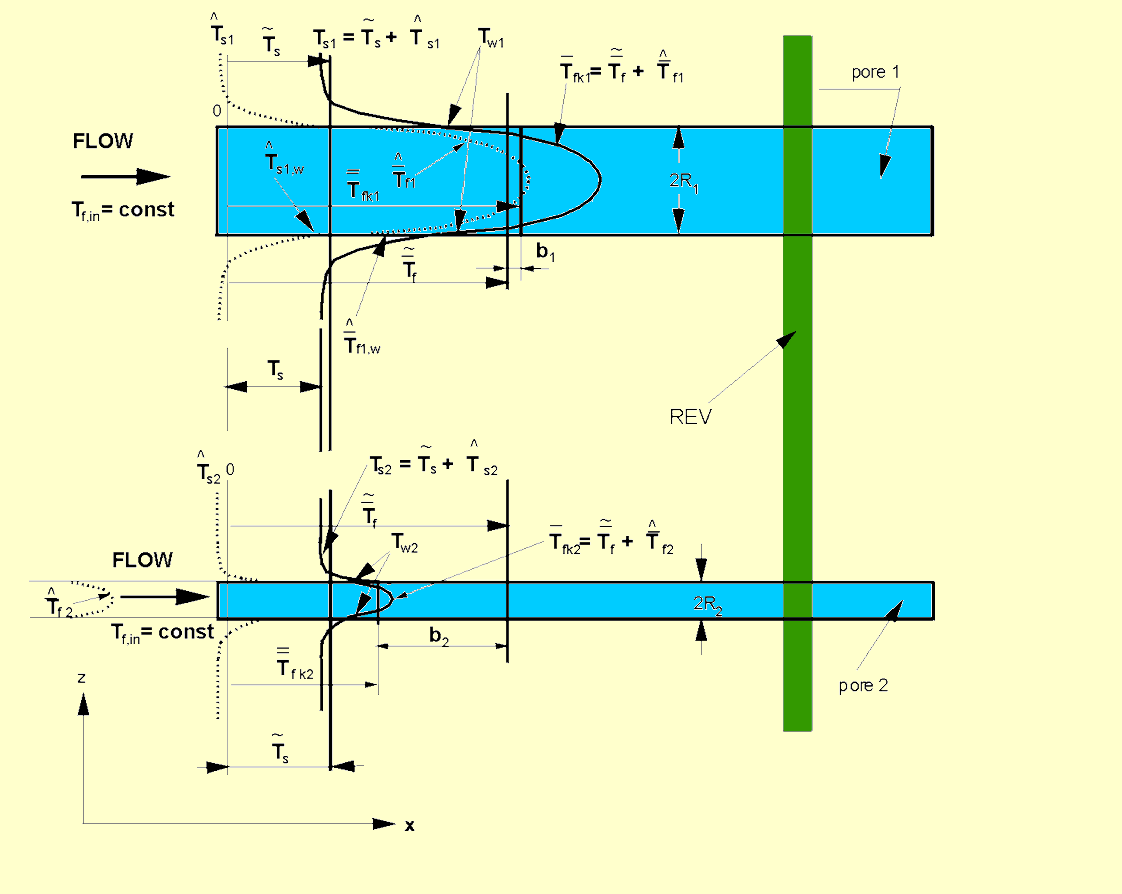
Fig. 2 Temperatures local and upper scale non-local calculated for a system of two parallel pores with different diameters within the straight parallel capillary morphology model of porous medium
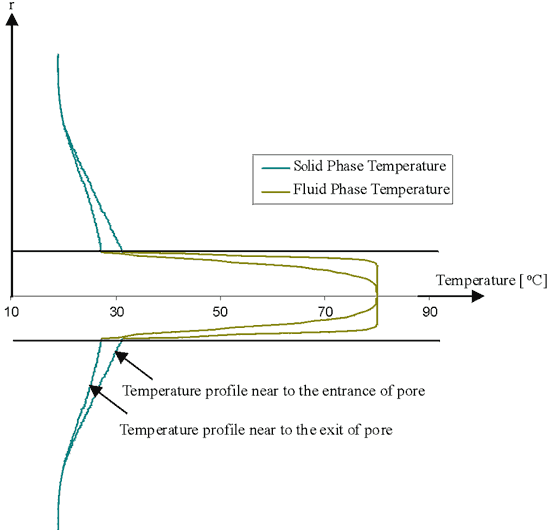
Fig. 3 Lower scale temperature distribution in and around the separate pore
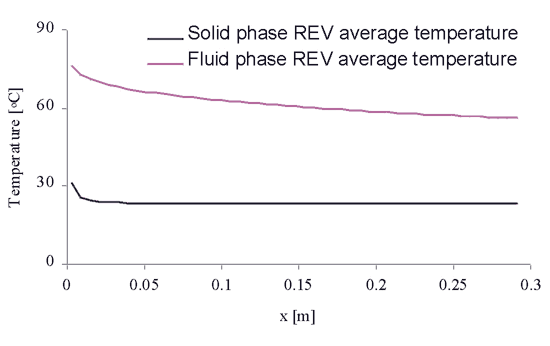
Fig. 4 Upper scale volume averaged temperature distribution
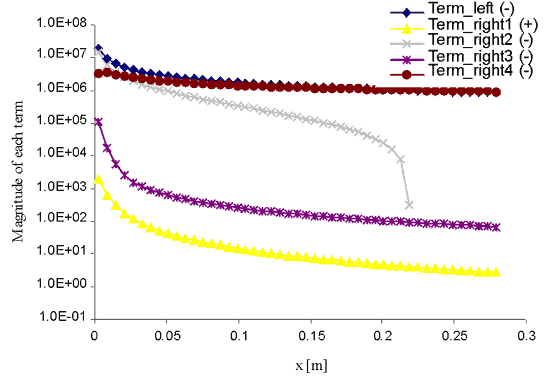
Fig. 5 Estimation of terms in the upper scale fluid phase heat transfer VAT equation
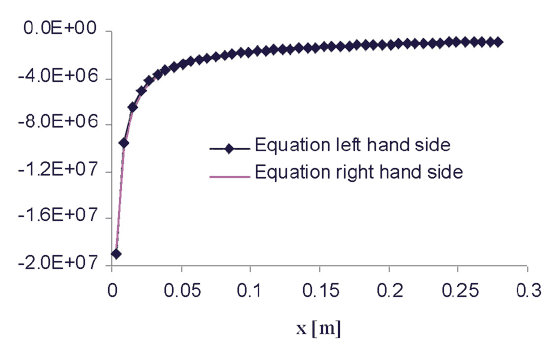
Fig. 6 Balance of the upper scale heat transfer VAT equation in fluid phase
ExactClosure-IMECE-2001-24261 (589K)
There can be a variety of location modes for globular particles exposed into the space. When a certain volume is fully occupied by an unconsolidated highly porous medium composed of uniform packed spheres an immediate interests lie in the prediction of phenomena pertaining to the case of large heat conductivity coefficients ks/kf ratios. The specific case and physical parameter values considered well describe that of a steel spherical-bead matrix with incompressible air entering the interstices by forced non-Darcy convection.
Some of the results were in - Gratton, L., Travkin, V.S., and Catton, I., ''The Influence of Morphology upon Two-Temperature
Statements for Convective Transport in Porous Media,''
Journal of Enhanced Heat Transfer, Vol. 3, No. 2, pp.129-145, (1996)
ENHNC-2002 (516K)
Few results from the rather substantial study by Travkin and Kushch exploiting the exact closure and solutions for globular morphologies can be seen in the following excerpt - Globular Morph
and in the following subsection in Heterogeneous Electrodynamics section
at this web site -
Electrodynamics::Globular Morphology Two Scale Electrostatic Exact Solutions
This is a simple 1D morphology, which, nevertheless have a great number of applications in various engineering fields -
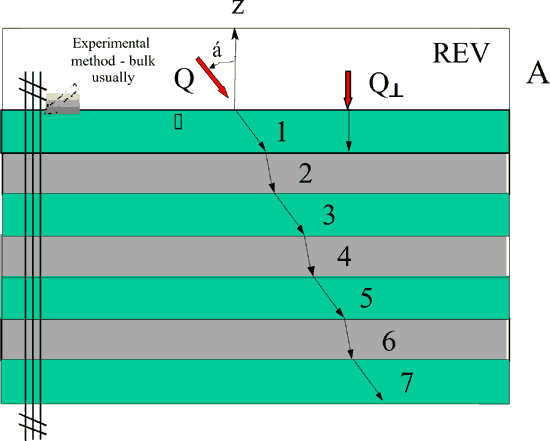
Fig. 7 Layered regular 1D medium (2 different component layers) lower scale flux flow with perfect interface conductance
As we wrote in the sub-section on education, in the example which is taken from the widely used undergraduate textbook on physics by Halliday et al. (2005) (textbook used and for biology students teaching), we can find the basic general rule for the heat (mass) transfer through the multilayer wall - "Conduction Through a Composite Slab...." in p. 494 as the formula (18-37)
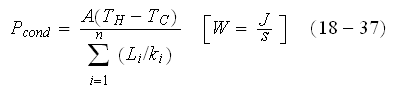
which is for unit surface

![$A=1[m^{2}]$](/edu/pic/right1__2.gif) in SI units can be presented as
in SI units can be presented as
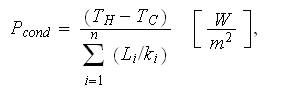
with the effective bulk medium coefficient of conductivity
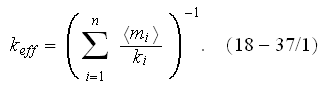

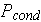 is the heat flux through the multilayer wall with fixed external surfaces
temperatures
is the heat flux through the multilayer wall with fixed external surfaces
temperatures

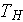 - the hot wall's surface and
- the hot wall's surface and

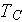 is the cold one, and
is the cold one, and

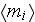 volume fraction of the i-th phase..
volume fraction of the i-th phase..
Authors of this example problem - which is the Two-scale problem, do not tell
the students that the formula

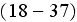 hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
1) that this is the two-scale actually problem;
2) the Upper (the second) scale solutions are not achievable in brackets of homogeneous physics. There are no definitions and mathematics (at least correct ones) for that in homogeneous physics;
3) the steady-state mean heat flux and the effective conductivity coefficient and of the transient problem ones are different by their definitions and scaled mathematics involved, not by only fact that those problems are different by time derivative and temperature depending on time;
4) the dependencies outlined in homogeneous physics solutions are incorrect if being applied with the exact fields for the lower scale solutions as, for example, the homogeneous formula gives the averaged difference temperatures (averaged gradients) that are not equal to the difference (gradient) of averaged temperatures
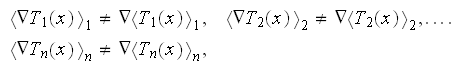
in spite that in homogeneous
physics they should be equal (here

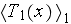 is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
Also, there is inequality one scale homogeneous physics can not explain
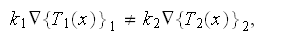
in spite that the homogeneous
thermal physics formula

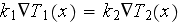 is correct (here
is correct (here

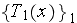 is the intrinsic phase averaged temperature,
is the intrinsic phase averaged temperature,

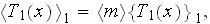 and
and

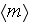 is the phase fraction).
is the phase fraction).
5) that for the linear problem there are the two physical mechanisms involved in field's transport - 1) is the INTRAPHASE, in each phase transport; and 2) is the INTERFACE transport each with their respective phase effective coefficients. These transport means and phase effective coefficients are not known in the one-scale homogeneous physics transport;
6) they don't tell the students that with this formula the transient problem can not be solved;
7) that there is no solution for this problem of mean heat flux (heat rate) in the transient formulated problem. The solution is achievable only via the two-scale physical and mathematical statement.
8) the formulae (18-37) and

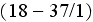 are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;
are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;
9) it might be impossible to design the optimal heat transfer or heat protection multilayer coating while study only the one scale Homogeneous statements. There is no one optimally designed yet - and that is the result of the more than hundred years effort!? That is why it can be stated the optimal design is unachievable when the one-scale thermal physics theory used.
Halliday, D., Resnick, R., and Walker, J., Fundamentals of Physics, 7th Ed., J. Wiley & Sons Int., (2005)
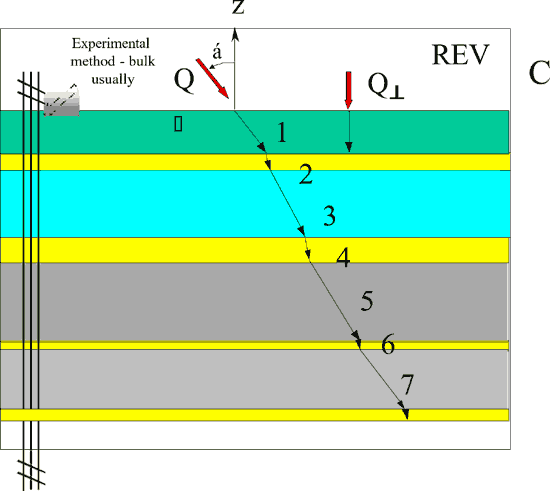
Fig. 8 Layered irregular 1D medium (n different component layers ) lower scale flux flow with perfect interface conductance
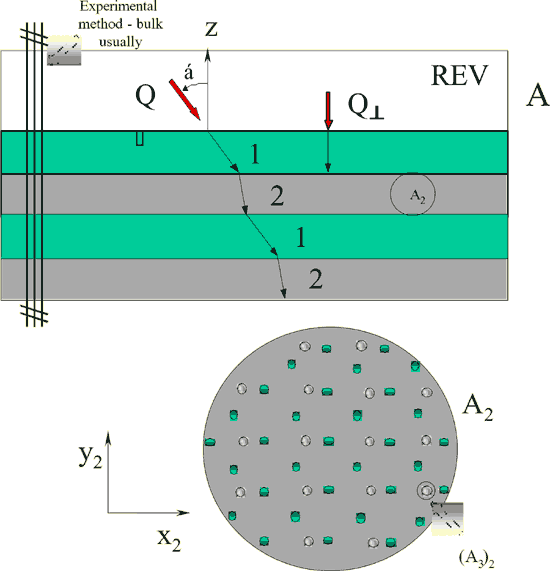
Fig. 9 Layered regular 1D medium (2 different component layers) lower scale flux flow with the second layer globulars of 3 kinds of amorphous substances (2 gradient and 1 isotropic phases)
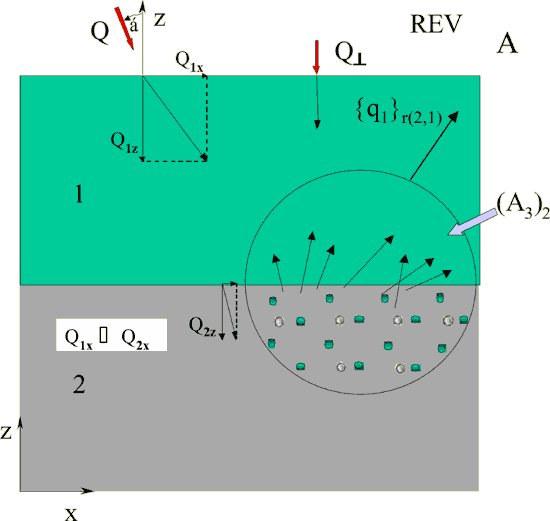
Fig. 10 The 3rd lower scale averaged EM field {q1}r21 reflected from the interface between the second and first layer
It is interesting to note that this the most reviewed and analyzed morphology when being considered as a two - scale problem is not going to support the known definitions and textbook formulae for the effective coefficients and bulk properties of the medium - see analysis in our - HEAT AND CHARGE CONDUCTIVITIES IN SUPERLATTICES - TWO-SCALE MEASURING AND MODELING (468K)
Doing further the research, for some of superlattice upper (bulk) scale problems
recently had been found the exact solutions.
The linear problems for electrostatics and thermal conductivity problems were solved in analytical forms for both scales.
Few results presented in the section devoted to Heterogeneous Electrodynamics
at this web site -
Electrodynamics::When the 2x2 is not going to be 4 - What to do?