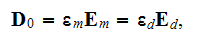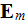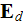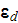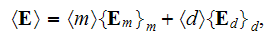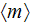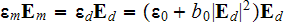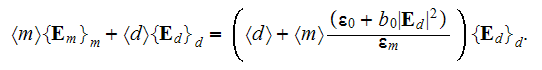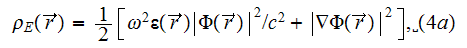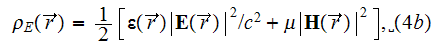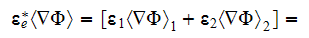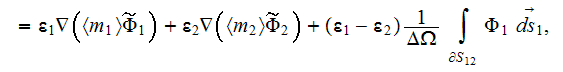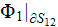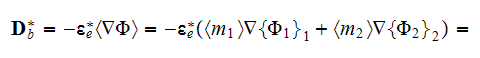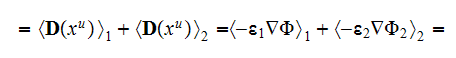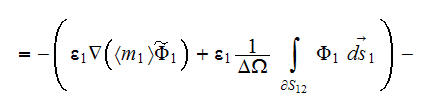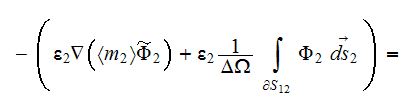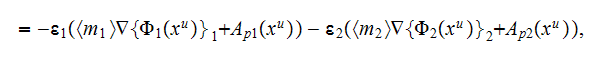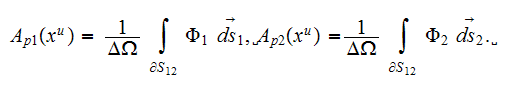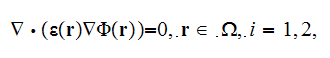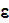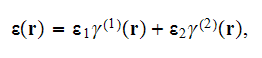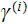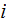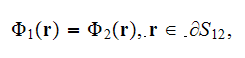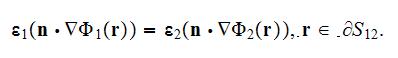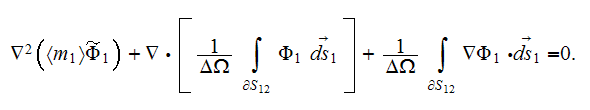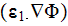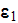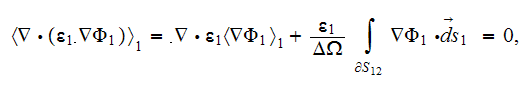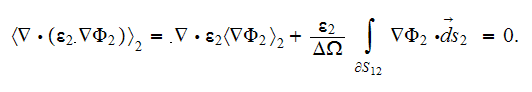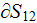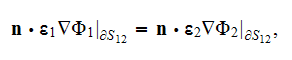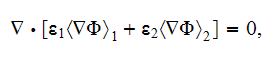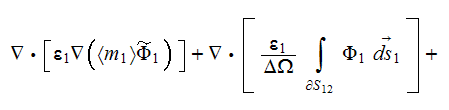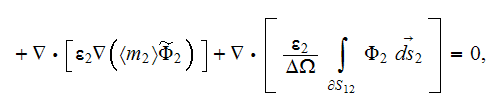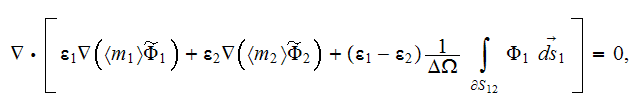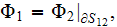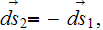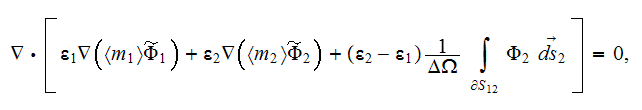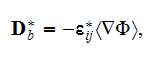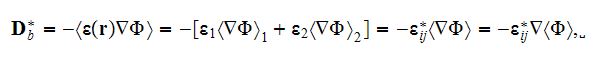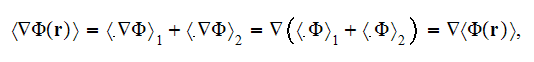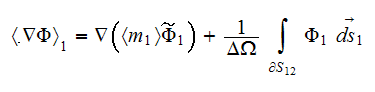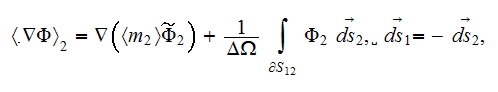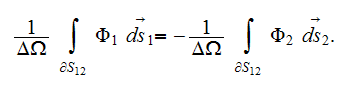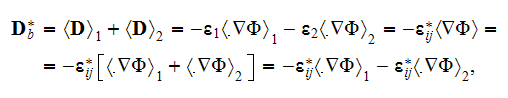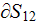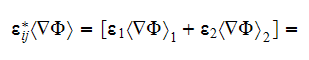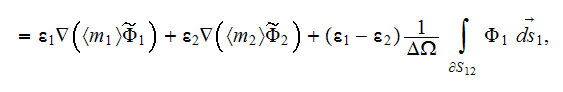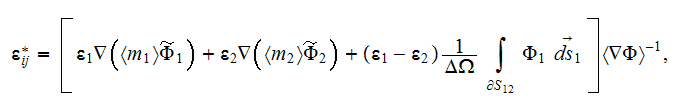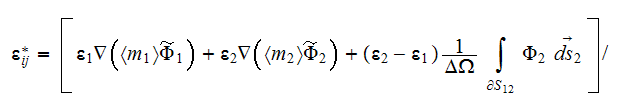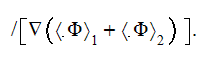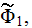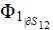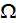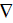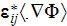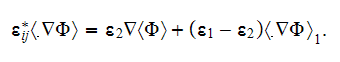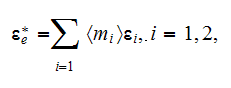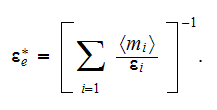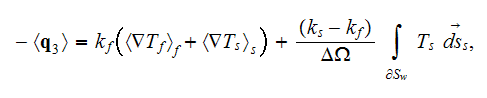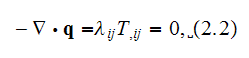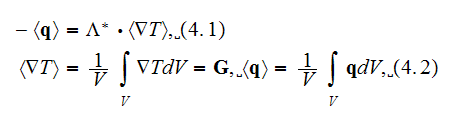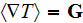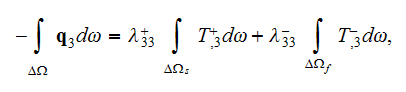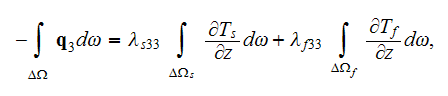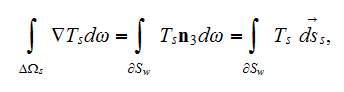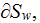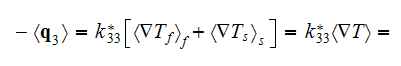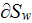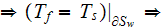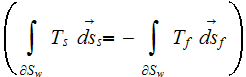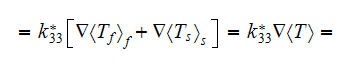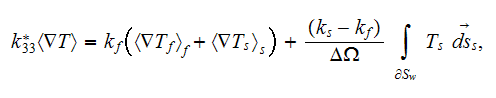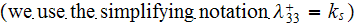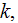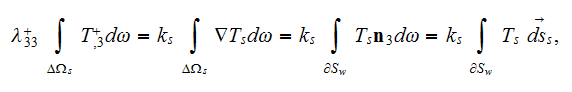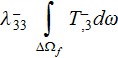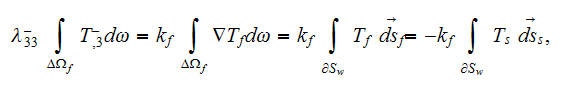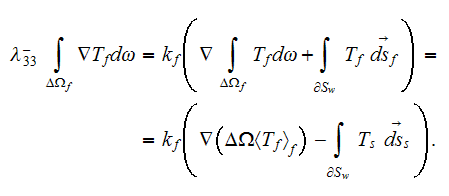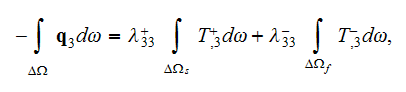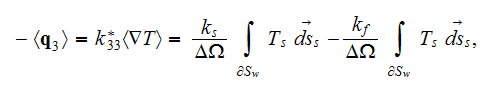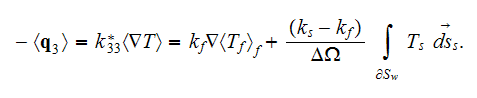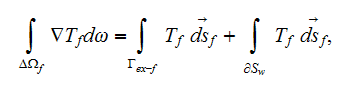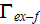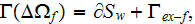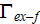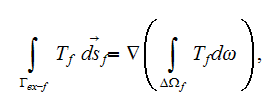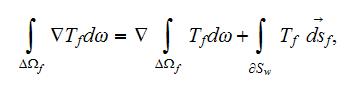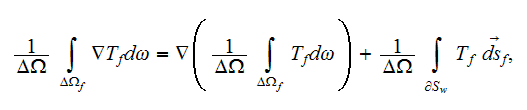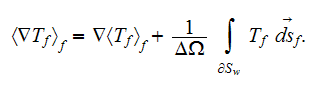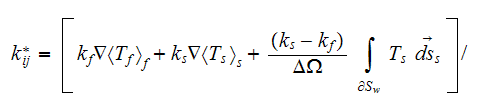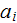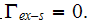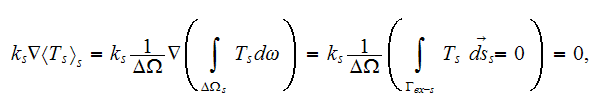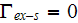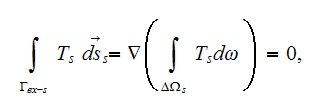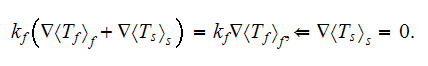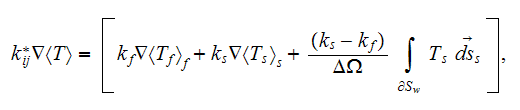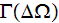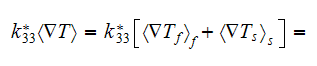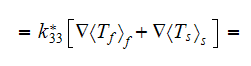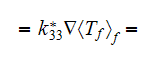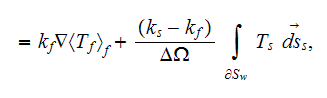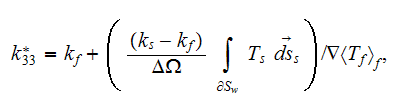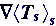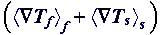The effective coefficients field is known to be the very useful area that allows us to connect, make a dependency between the two related physical characteristics, variables, or between the whole mathematical expressions.
When this issue is treated for the problem describing the mix of homogeneous more or less known dependencies
and the characteristics related to heterogeneous averaged (naturally) medium, then the details of each definition and parameter better to be clarified as to the specifics of each medium and problem.
And this is the most often situation occurred in applications, technologies, etc.
As we have seen already in the sections on Fluid Mechanics and Thermal Physics -
that the treatment of the effective coefficient issues must be done with the full two scale equations of the HSP-VAT problem taken into consideration.
There are number of reasons why we can not get along doing the same stuff in the HSP-VAT effective coefficient determination as in the homogeneous physics usually done for a long time.
As long as not every HSP-VAT electrodynamics equation and definition has been published we make
here a great deal of attention and provide few examples
with the works and expressions derived with the elsewhere written mathematics, as
this is done in the subsections -
Cross-Characteristics Modeling Explained in Terms of VAT
When the 2x2 is not going to be 4 - What to do?
Two Scale EM Wave Propagation in Superlattices - 1D Photonic Crystals.
We start with the homogeneous followed by heterogeneous formulation for the
effective coefficient as in
When the 2x2 is not going to be 4 - What to do?
Few the very important HSP-VAT statements developed above
should be reiterated here -
4) The upper (the second) scale solutions are not achievable in brackets of
homogeneous physics. There are no definitions and mathematics (at least
correct ones) for that in homogeneous physics. That is why there is
continuous search for experimental methods to measure the superlattice
conductivity and dielectric permittivity. For example, most of the latest
heat conductivity measurement methods use the transient try-and error fitting
techniques to match the measured bulk data while solving the lower scale
homogeneous transient heat conductivity equations. They calculate in this way
the different - the TRANSIENT homogeneous bulk heat conductivity coefficient.
That coefficient differs from a steady-state sought heterogeneous effective
coefficient. Also, with these techniques there is no way to find out the Phase
Effective Coefficients of conductivity or permittivity.
7) The dependencies outlined in homogeneous physics solutions are incorrect if
being applied with the exact fields for the lower scale solutions as, for
example, the homogeneous formula gives the displacement field in the system
through the averaged electric fields (potentials)
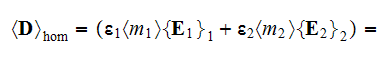
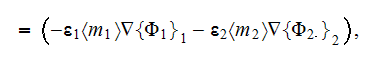
and
this value can be tens and hundreds times different from the correct one. We
are assuming here as usual that according to homogeneous Gauss-Ostrogradsky
theorem the following is true - the averaged

 over the each phase
over the each phase

 gradient operator acting on the potential function
gradient operator acting on the potential function

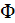 is equal to
is equal to
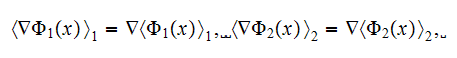
which is incorrect!
8) The known "classical" formulae for "in-series" two phase 1D composite
effective coefficients can be calculated as known for bulk values only for
linear problem. It is important to say that the formula for the linear
effective bulk coefficient
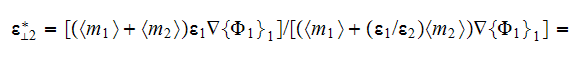
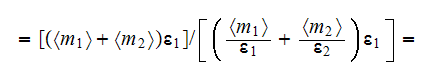
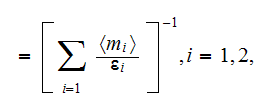
is correct, but is not valid for the derivation! Final
result and the formula is correct, but the derivation is not correct ? It can
not be derived even for linear problem when applied only the one scale
homogeneous knowledge base.
That is because

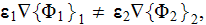 in spite that the homogeneous fields formula
in spite that the homogeneous fields formula

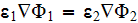 is correct.
is correct.
9) The simple particular layered morphology of the two-scale problem dictates
the peculiarities of the physical phenomena involved. Thus, for the linear
problem there are the two physical mechanisms involved in field's transport
- 1) is the INTRAPHASE, in each phase; and 2) is the INTERFACE transport. In
most common situations those are the three different components in the
transport characteristics. The later properties described and accounted for as
to the physical phenomena seems only in chemistry, chemical technology.
In electrodynamics it is still considered as the 3D phenomena of a one scale.
11) The mathematical formulation and exact calculation of the surficial
transport components gives an expected explanation of decreased overall bulk
permittivity and what is more important is of their magnitudes. It also
allows to compare transport in each separate phase along with their
components.
12) Needless to say, that the unknown component of interface transport can
reach values of hundreds and even thousands percent of effective bulk values -
see Figs. 2,3 in -
When the 2x2 is not going to be 4 - What to do?
That can be directed toward the explanation of some known
physical phenomena as, for example, like the interface resistance and
polarization among others.
From numerous works on effective coefficients for electrodynamic
problems we can select just few, no matter of whom, but rather of known people and
see - what is considered as an "effective" coefficient when homogeneous GOT being
used and applied for this when the media are Heterogeneous.
For example, in the paper by Tao et al., (1990) we see a good solution of the same kind of model - the homogeneous One scale commonly known mathematical model for a heterogeneous media of the two kinds
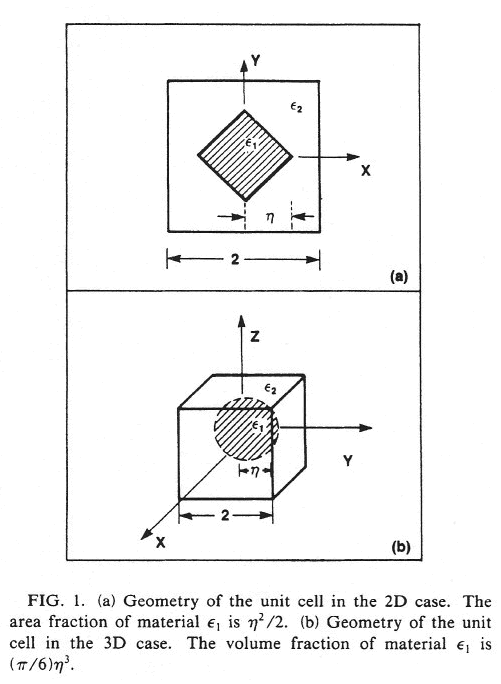
which we see in the page 2419.
As we analyze below the one of the best studies of effective coefficients problem done by Kushch, these coefficients in work Tao et al. (1990) (and in other lower scale homogeneous models) nothing more as the quazi-"effective" one scale coeffiicents. They are not correctly averaged characteristics.
But what about the experiements assessment, more or less good comparisons and such in homogeneous electrodynamics - one would ask?
Well, the problem also is with the experimental set up.
It is also done with the same theoretical ground of Homogeneous conseptions - so,
What else you would expect in return ?
In the next paper by Bergman and Dunn (1992) in the p.13262 we can read about
calculations of the effective dielectric permittivity in the previous work
-"In practice, the results for

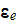 were often not better than those found by using the simple Clausius-Mossotti
or Maxwell-Garnett (MG) approximation, which ignores almost all the details of
the microgeometry."
were often not better than those found by using the simple Clausius-Mossotti
or Maxwell-Garnett (MG) approximation, which ignores almost all the details of
the microgeometry."
We would say - And not only of microgeometry, but principally is of not
averaged fields, simply incorrect.
Also in that page 13262: "In this article, we propose another method for
calculating

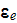 of such composites in the quasistatic regime. Our method also uses the Fourier
coefficients of
of such composites in the quasistatic regime. Our method also uses the Fourier
coefficients of

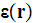 at reciprocal-lattice values of
at reciprocal-lattice values of

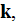 and is therefore applicable to quite general, periodic microgeometries. "
and is therefore applicable to quite general, periodic microgeometries. "
That is incorrect statement as we see in many places of this website. This is
the same Lower scale "quasi-averaged" "effective" coefficient see also in -
In one of HSP-VAT formulations the bulk dielectric permittivity effective
coefficient for the two phase medium we can calculate as via
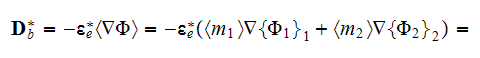
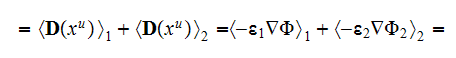
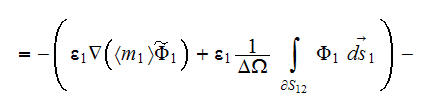
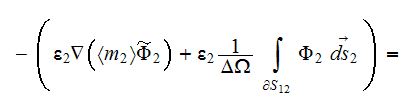
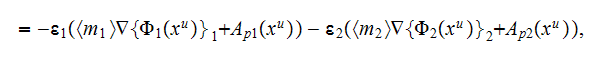
where as we defined above
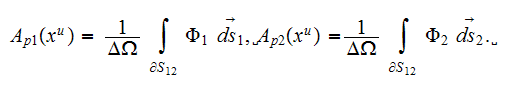
Writing here few basic formulae for the dielectric medium statement which
usually utilized while applying the Detailed Micro-Modeling - Direct Numerical
Modeling (DMM-DNM) for a heterogeneous medium on the Lower Scale
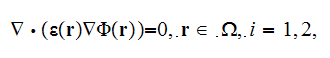
where the dielectric coefficient

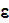 is the piece-wise function
is the piece-wise function
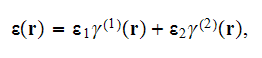
and

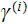 is the characteristic function of phase
is the characteristic function of phase

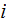 .
Interface boundary conditions assumed for this statement are
.
Interface boundary conditions assumed for this statement are
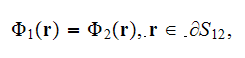
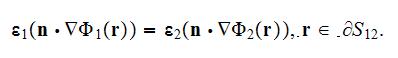
The mathematical statement in the DMM-DNM approaches usually deals with the
local fields and as soon as the boundary conditions are determined in some
way, the problem became formulated correctly and can be solved exactly.
Difficulties arise when the result of this solution needs to be interpreted -
and this is in the majority of problem statements in heterogeneous media, in
terms of non-local fields, but averaged in some way. The averaging procedure
usually is proclaimed in one of the fashions - either doing stochastic or
spatial, volumetric integration. Almost all of these averaging developments
are done incorrectly due to disregard of averaging theorems for differential
operators in heterogeneous medium.
Secondly, as soon as the boundary surfaces are intersecting both of the phase
subvolumes, the conventional boundary conditions become invalid as well as the
DMM-DNM solution. In the event when boundary surfaces are chosen to belong to
only one of the phases in a random or irregular morphology medium the problem
becomes formulated as in a special kind of periodic medium and its solution
has peculiarities and useful value for the problem stated only with
the one phase boundary condition. When a problem's physical model
includes phenomena of wave propagation through the boundary of heterogeneous
body as, for example, in most of electromagnetic problems, the one phase
boundary condition has no value for that problem.
Meanwhile, if the coefficient of dielectric permittivity in the phase one is a
constant value then the upper scale VAT equation for potential field in this
phase is
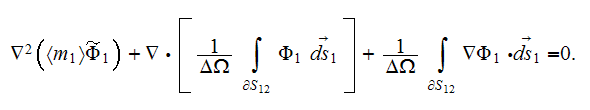
The steady-state equation in the phase one in terms of potential flux

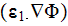 when
when

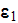 is a constant looks like
is a constant looks like
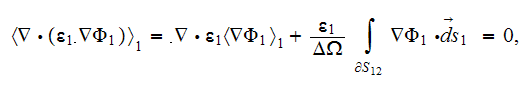
and in the second phase the same kind of potential equation
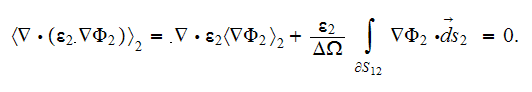
Observing these equations one can assume that the effective permittivity
coefficient in a medium should come from the equation of sum of the previous
equations for each phase which can be reduced consecutively accounting for the
conservation of displacement field at the interface

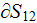
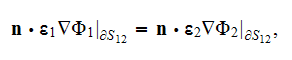
then we can summarize
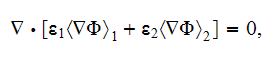
or
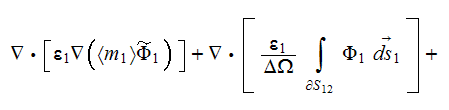
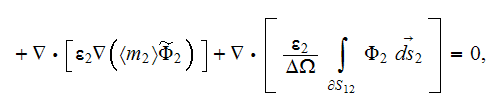
which results in
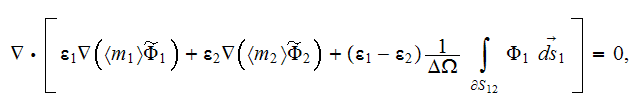
because

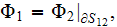 and
and

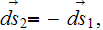 also the same kind of expression can be obtained
also the same kind of expression can be obtained
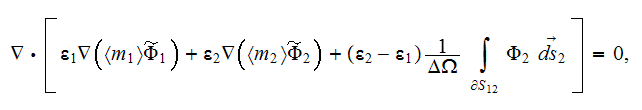
assuming that the phase two is the globular inclusions phase. Standard
definition for effective (macroscopic) permittivity (or conductivity) tensor
determines from the following equation
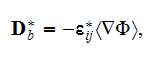
in which assumed that the displacement field vector can be presented as
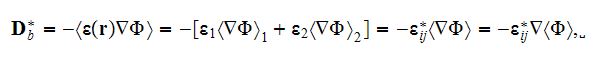
as soon as for the standard BC
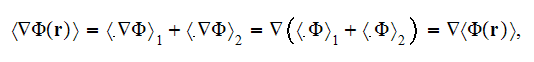
because
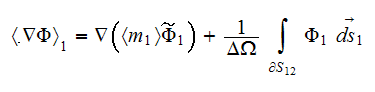
and
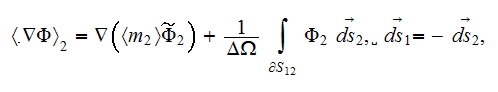
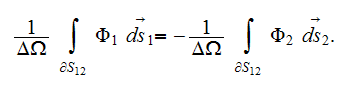
Further, we assume that
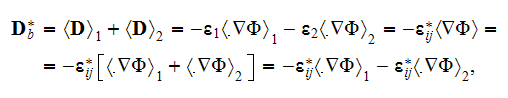
and, for the usually assumed at the interface

 physics the effective coefficient determines as
physics the effective coefficient determines as
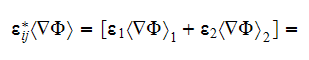
|  |
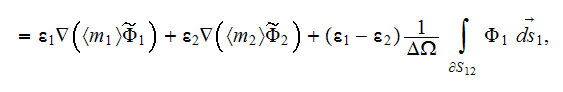 | (1) |
or
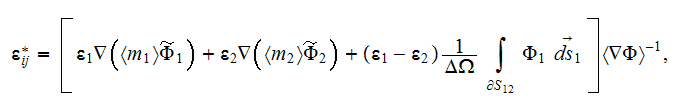
or
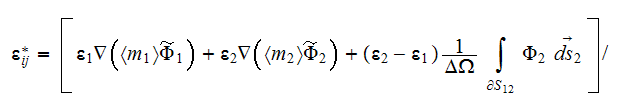
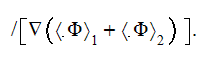
involving knowledge of the three different potential functions

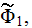

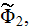 and
and

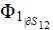 in the upper scale space consideration in the volume
in the upper scale space consideration in the volume

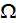 and at the
interface
and at the
interface
 This formula for the steady state effective permittivity can be shown is equal
to the known expression
This formula for the steady state effective permittivity can be shown is equal
to the known expression
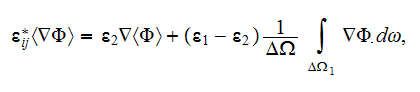
which means, when applied the WSAM theorem for averaging the operator

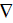 then
then

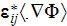 is equal to
is equal to
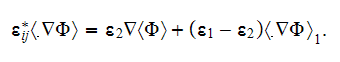
This is one of the evidences that for some (very few) instances there can be
drawn the direct analytical comparison of homogeneous and heterogeneous
formulae. For this particular above formula the comparison shows the
coincidence. We will demonstrate below for the layered medium one more example
of a complete inheritance and conjugation for homogeneous and heterogeneous
descriptions.
It is worth to note here that the known formulae for the effective dielectric
permittivity (or conductivity) of the layered medium
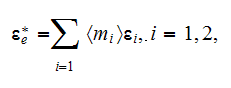
for electric field applied in parallel to interface of layers, and
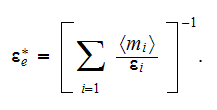
when an electric field is perpendicular (in-series) to the interface, can be
derived from the general expression (1) but only for linear medium (constant
coefficients).
The following is the analysis of outstanding work by one of the workers who
while having familiarity with the HSP-VAT had done the study with the wrong
application of the homogeneous GO theorem, regarding the effective coefficient
finding.
In his work Kushch (1997a) described in some misleading text pieces the
mathematical procedure for calculation of the effective coefficients of
conductivity (dielectric permittivity, diffusivity, etc.) in globular media. In pages 67 and 70 author
described few main points in assessment (simulation) of the thermal bulk effective
conductivity for the two-phase composite with spherical inclusions as a second
discontinuous phase.
Doing that, author firstly included in his text some elements of VAT, for
example, on page 70 is given the formula for the component of bulk thermal
flux
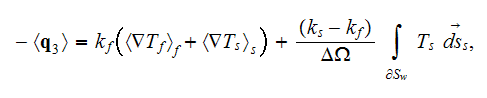
with the surface integral. This combination of the surface integral and
averaged temperature gradients in each of the phases could appear in the
formula only because of heterogeneous WSAM theorem. But not because of the use
of the homogeneous GO theorem. Author does not tell about this feature to a
reader.
Author intentionally avoiding using the VAT language, for example, in equation
(2.2)
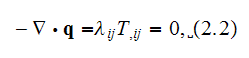
and while writing formulae (4.1), (4.2)
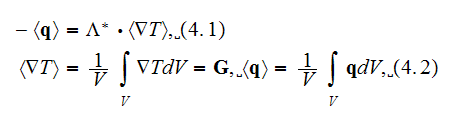
he does not tell that those two groups of definitions are from different
spaces. That is - his effective coefficient is applicable to the only
condition of a thermal equilibrium for both phases, when the steady-state
thermal circumstances have been established, see more explanation in Travkin
(1998, 2001a,b) (2001a - Travkin, V.S., "Discussion: "Alternative Models of
Turbulence in a Porous Medium, and Related Matters" (D. A. Nield, 2001, ASME
J. Fluids Eng., 123, pp. 928--931)," J. Fluids Eng.,
Vol. 123, pp. 931-934, (2001a)).
Author also does not tell to a reader - How the "average gradient"

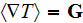 is described mathematically for the two-phase matter, while it is very
important for assessments and analysis of few "effective" coefficients
existing for this problem.
is described mathematically for the two-phase matter, while it is very
important for assessments and analysis of few "effective" coefficients
existing for this problem.
Starting with the volume integration of the heat flux as in
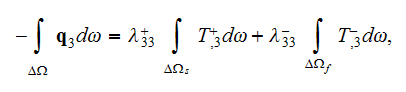
which is in VAT notations
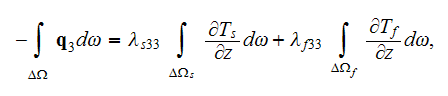
and using only the GO homogeneous medium theorem like
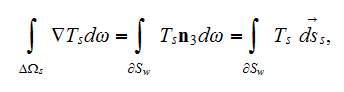
where the normal vector

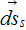 is directed outward from the solid-fluid (particle-matrix) phase interface
surface
is directed outward from the solid-fluid (particle-matrix) phase interface
surface

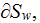 Kushch derived on page 70 for the regular globular inclusions composite using the declaration that
the formula for the effective coefficient of conductivity as for the one (in
z) direction has to be
Kushch derived on page 70 for the regular globular inclusions composite using the declaration that
the formula for the effective coefficient of conductivity as for the one (in
z) direction has to be
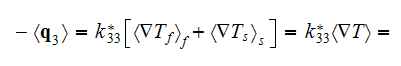
which according to equality of temperatures at the

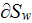

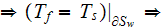

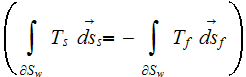
gives
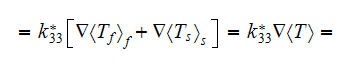
and further Kushch "obtains"
|  |
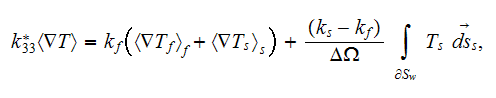 | (2) |
referring to the GO theorem when doing spatial integration over the particle (

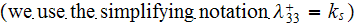 with the more often used in western literature notation for coefficient
of thermal conductivity
with the more often used in western literature notation for coefficient
of thermal conductivity

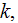 )
he gets
)
he gets
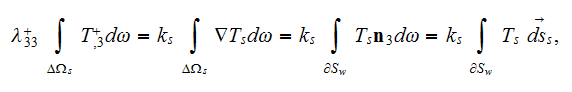
and what is the most interesting is the integration over the matrix (fluid)
phase sub-volume

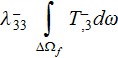 ;
with
;
with

 which is according to usual GO theorem should looks like
which is according to usual GO theorem should looks like
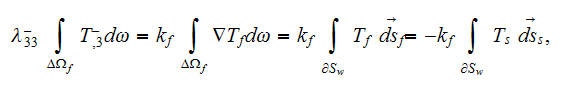
but which should be done according to WSAM theorem as
|  |
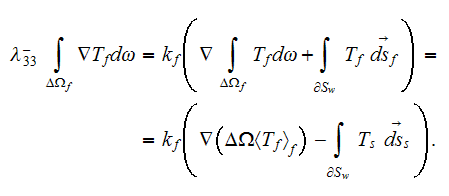 | (3) |
Now, let we try to obtain the same (2) from the initial fluxes integration equality
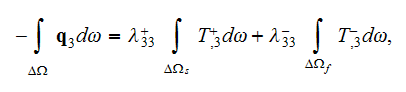
and following the derivation path recommended by Kushch. Then we get
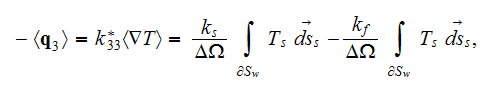
and which is obviously not going to coincide with the Kushch's (2) ?
To go to the real derivation path used by Kushch we need to use the (3) which
is using the WSAM theorem and getting
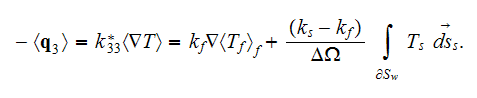
Meanwhile, this expression is still not the same as (2) ?
We need to go deeper into the mathematics hidden in the paper by Kushch
(1997) intentionally. Why he did that?
Because he did not want to show the HSP-VAT derivation path and averaging VAT notations, refer to the new to him at that time (94-96) VAT modeling and scaled averaging mathematics, thus doing gaps in the mathematics derivation and in the explanations of the resulting formulae.
Still, we need, first of all, the few explanations following the WSAM theorem's consequences.
The above derivations are possible because for the matrix phase as soon as
according to the GO theorem we have the equality
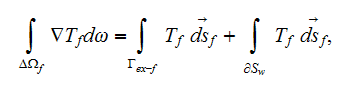
where

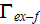 is the surface of entrance and exit for the phase-f at the boundary surface of
the REV suggested by Kushch
is the surface of entrance and exit for the phase-f at the boundary surface of
the REV suggested by Kushch

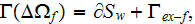 so further we have according to the WSAM theorem that the surface integral
over the input-output surface
so further we have according to the WSAM theorem that the surface integral
over the input-output surface

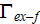 is equal
is equal
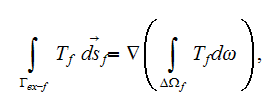
then, substituting this equality into the previous regular homogeneous GO
theorem based formula we have
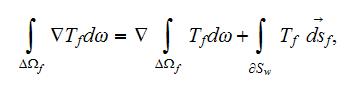
dividing this expression's both side parts by

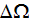 we get
we get
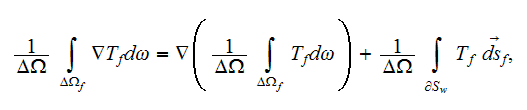
or
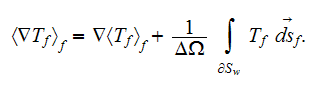
We need to show further that we can not get this equality (2)
using only the homogeneous medium GO theorem.
To show this, let we start from the general correct (with the
used WSAM theorem) formula for the effective conductivity coefficient in the
two-phase linear heterogeneous medium (constant properties)
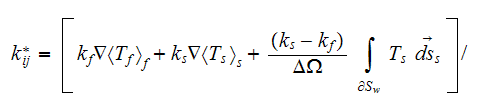
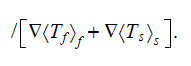
and realizing that the morphology of the medium and the REV does not connect
the solid phase to the bounding REV surface

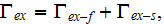 when that for the specifically carved in this work REV (on p. 70 - "For a
periodic composite the elementary structure cell, in the form of a
parallelepiped with sides
when that for the specifically carved in this work REV (on p. 70 - "For a
periodic composite the elementary structure cell, in the form of a
parallelepiped with sides

 containing one particle, can be chosen as the representative volume.")
containing one particle, can be chosen as the representative volume.")
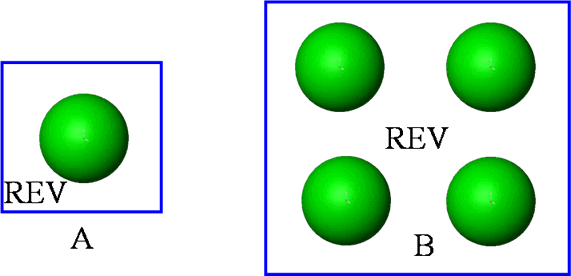
with the external particle-matrix interphase surface equal to zero

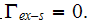
That means using the WSAM theorem and keeping in mind
that we have the only this arrangement for the REV we can write
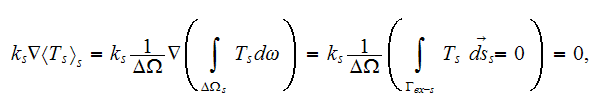
as soon as

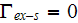 though we have that
though we have that
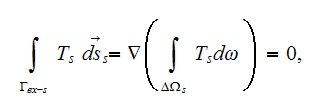
and that means - we can get right for this case, when the REV has the spatial location as it does not intersect with the solid phase - the spheres, the equality
which is
|  |
 | (4) |
So, these are the reasons why Kushch used the formula for the effective
conductivity in only such a form (2).
But it is unrealistic - to have only such a special
REV's locations, right ? This means - the case sensitive only partial solution
has been obtained.
And generally this is not the full formula for this
coefficient. As long as we can have the real general legitimate arrangements -
when the REV's

 would intersect the both phases -
would intersect the both phases -

Then, that means we need to use the general formula for the steady-state effective
conductivity coefficient followed from the WSAM theorem
and use the same algorithms as we used for the
superlattice coefficient !
This formula above (2) (by Kushch (1997a)) for the REV with the external surface

 going through the matrix (fluid) only (with the inclusions inside)
going through the matrix (fluid) only (with the inclusions inside)

still should be written
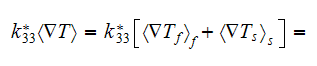
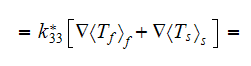
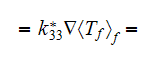
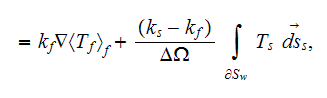
so - it can be written also as
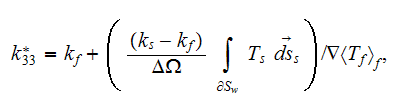
with the one differential term:

 at the r.h.s.!
at the r.h.s.!
This is the very important distinction from the formula by Kushch (2).
But Kushch did this because the part

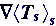 of
the sum (4) is equal to zero, and that gave him the ability to use the
generalized formulae for the effective coefficients, using the general
averaged gradient
of
the sum (4) is equal to zero, and that gave him the ability to use the
generalized formulae for the effective coefficients, using the general
averaged gradient

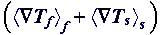 .
.
At the same time he explained nothing in the paper (Kushch, 1997a) about the WSAM theorems that only gave him a chance (comparing to his previous studies on the same
topic - Kushch, 1991, 1994, and other studies on composites elasticity and strength) to make this research possible !?
Still, with the wrong Effective Coefficient tables - because the final averaging formulae had been done incorrectly.
Summaries:
From this lengthy analysis we can get at least three useful conclusions.
1) First is that the all effective coefficients obtained for heterogeneous
media with mathematics based on the homogeneous GO theorem give incorrect
results!
This is the pretty strong message and I will use it with all my respect to the
authors of those incorrect studies and for a while. For example, the
excellent DMM-DNM study by Cheng and Torquato (1997) done for kinds of medium as
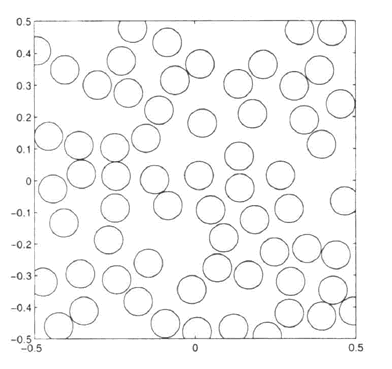
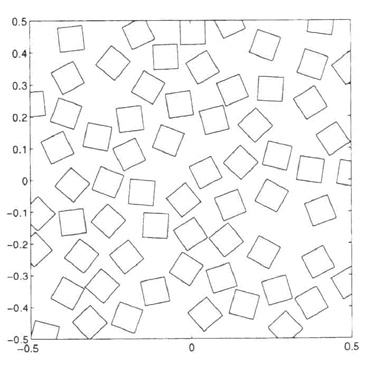
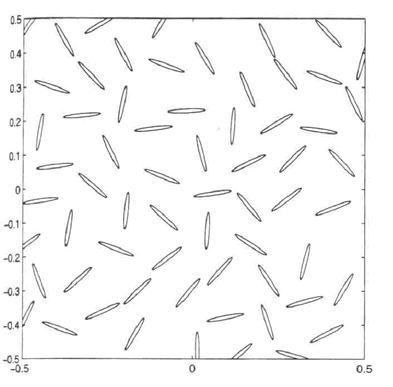
then, when the results of DMM-DNM of the Lower scale applied toward the obtaining
the effective coefficient the assessments would give incorrect outcome due to
the reasons we pointed to above.
2) The second conclusion is that even the usage of WSAM theorem, but
incorrectly, as done by Kushch (1997) brings out the incorrect effective
coefficients also !
3) What is the difference, the correction to the homogeneous Lower Scale "effective"
coefficients to get to the sought after the Heterogeneous Upper Scale effective coefficients?
This is the subject of each specific problem consideration and of the two scale solution.
References:
Bergman, D.J. and Dunn, K.-J., "Bulk Effective Dielectric Constant of a Composite
with a Periodic Microgeometry,"
Physical Rev. B, Vol. 45, No. 23, pp. 13262-271, (1992).
Bergman, D.J., Levy, O., and Stroud, L., "Theory of Optical Bistability in a
Weakly Nonlinear Composite Medium,"
Phys. Rev. B, Vol.49, No. 1, pp. 129-134, (1994).
Busch, K. and Soukoulis, C.M., "Transport Properties of Random Media: A New
Effective Medium Theory,"
Phys. Rev. Lett., Vol. 75, No. 19, pp. 3442-3445, (1995).
[8] Fokin, A.G. Macroscopic Conductivity of Random Inhomogeneous Media.
Calculation Methods//Physics - Uspekhi. 1996. V. 39, N. 10. P.1009-1032.
[11] Cheng, H. and Torquato, S. Electric-field Fluctuations in Random
Dielectric Composites//Phys. Rev. B. 1997. V. 56, N. 13. P. 8060-8068.
[50] Kushch, V.I., "Conductivity of a periodic particle composite with
transversely isotropic phases," Proc. R. Soc. Lond., A
453, pp. 65-76, (1997a).
Kushch, V.I. and Artemenko, O.G., "Determination of Temperature Field in a
Granular Layer," Doklady AN Ukr. SSR, No. 3, pp.74-77,
(1983), (in Ukrainian).
Kushch, V.I., "Stressed State and Elastic Moduli of a Periodic Composite
Reinforced By Coated Spherical Particles," Mechanics of
Composite Materials, Vol. 29, No. 6, pp. 816-822, (1993), (in Russian).
[51] Kushch, V.I., "Microstresses and Effective Elastic Moduli of a
Solid Reinforced by Periodically Distributed Spheroidal Particles'', Int. J.
Solids Structures, Vol. 34, No. 11, pp. 1353-1366, (1997b).
Kushch, V.I., "Heat Conduction in a Regular Composite With Transversely
Isotropic Matrix," Doklady AN Ukr. SSR, No.1,
pp.23-27, (1991), (in Ukrainian).
Kushch, V.I., "Thermal Conductivity of Composite Material Reinforced by
Periodically Distributed Spheroidal Particles," Engng.-Phys.
Journal, Vol. 66, 497, (1994), (in Russian).
Kushch, V.I., "Elastic Equilibrium of a Medium Containing Finite Number of
Aligned Spheroidal Inclusions," Int. J. Solids
Structures, Vol. 33, No. 8, pp.1175-1189, (1996).
Golovchan, V.T., Guz', A.N., Kokhanenko, Yu.V., and Kushch, V.I.,
Mechanics of Composites. T.1. Statics of Materials,
Kiev, Naukova Dumka, 1993, 455pgs, (in Russian).
Tao, R., Chen, Z., and Sheng, P., "First-Principles Fourier Approach for the Calculation
of the Effective Dielectric Constant of Periodoc Composites,"
Phys. Rev. B, Vol. 41, No. 4, pp. 2417-2420, (1990).
[33] Travkin, V.S. and Catton, I., "Porous Media Transport Descriptions - Non-Local, Linear and Non-linear Against Effective Thermal/Fluid Properties//
Advances in Colloid and Interface Science," Vol. 76-77, pp. 389-443, (1998).
Travkin, V.S., "Discussion: "Alternative Models of Turbulence in a Porous Medium, and Related Matters," (D.A. Nield, 2001, ASME J. Fluids Eng., 123, pp. 928-931),"
J. Fluids Eng., Vol. 123, pp. 931-934, (2001a).
Travkin, V.S. and Catton, I., "TRANSPORT PHENOMENA IN HETEROGENEOUS MEDIA BASED ON VOLUME AVERAGING THEORY",
in Advances in Heat Transfer, Vol. 34, pp. 1-144, (2001b).
Travkin, V. S. and Ponomarenko, A. T., "Electrodynamic Equations for Heterogeneous Media and Structures on the Length Scales of Their Constituents", Inorganic Materials, Vol. 40, Suppl. 2, pp. S128 - S144, (2004).
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 7-17, (2005).
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005).
Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005).
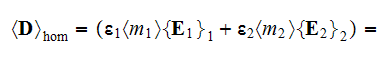
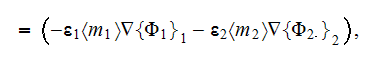

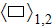 over the each phase
over the each phase

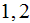 gradient operator acting on the potential function
gradient operator acting on the potential function

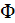 is equal to
is equal to
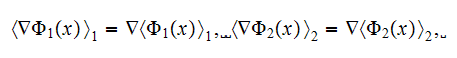
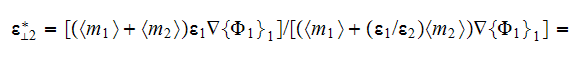
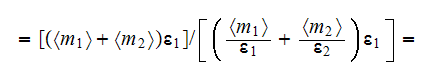
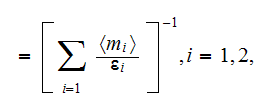

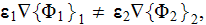 in spite that the homogeneous fields formula
in spite that the homogeneous fields formula

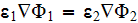 is correct.
is correct.


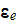 were often not better than those found by using the simple Clausius-Mossotti
or Maxwell-Garnett (MG) approximation, which ignores almost all the details of
the microgeometry."
were often not better than those found by using the simple Clausius-Mossotti
or Maxwell-Garnett (MG) approximation, which ignores almost all the details of
the microgeometry."

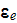 of such composites in the quasistatic regime. Our method also uses the Fourier
coefficients of
of such composites in the quasistatic regime. Our method also uses the Fourier
coefficients of

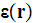 at reciprocal-lattice values of
at reciprocal-lattice values of

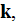 and is therefore applicable to quite general, periodic microgeometries. "
and is therefore applicable to quite general, periodic microgeometries. "