Many problems formulated for globular morphology serve as the test problems in physical disciplines. The globular morphology problems belong to the noble category of problems (as the plane layers problems) which used to obtain an exact solution or to verify or compare already known solutions when new ideas, method or theory appeared.
We used this kind of problems for the same purpose. When in 90-th the challenge was put before to show the practical purpose (purposes) 2 scale problems, which are of the general understanding and at the same time due to the nature of the two-scale statement should bring out the useful results that was believed can not be seen via the homogeneous one scale problem formulation, I had been tackling with problems in few fields. One of them was the globular morphology medium embedded in a matrix or in a surrounding laminar flow fluid (turbulent flow would involve many related complicated issues).
Another group of problems that was studied with details and thorough attention to features those would state questions regarding the closure procedures and about the two-scale simulations was the pretty many times problem probed by strong people - the conduction-diffusion-potential distribution of fields in the regular, and/or with defects, and/or with spatial properties change spherical particles two-phase medium.
Applications of these Globular Morphology test problems are everywhere, not only in Fluid Mechanics, Thermal Physics, Electrodynamics, etc. as traditionally can be sought. Many times more expensive while also principal are applications in biological sciences.
Again, as I said those problems were approached many times with different theories and models. My intention was not only to solve the problem on one of the scales - myself and my collaborator at that time Dr. V.I.Kushch had been looking for the solutions on the both scales, and for comparison with other known solutions for this class of problems. We need to remember, that the solution of the Two-Scale problem only over the one scale is defective either for one or another scale solution. The only good results obtained when the information for closure is known somehow from the another scale.
That is why the solution of the lower scale problem is in no way constitutes the all over knowledge for the Upper scale properties for those models. Meanwhile, people usually solve the lower scale problem just for the upper scale assessments!
I have the sincere desire to say that we had solved these problems with the best techniques available, and with the highest accuracy. Below I would discribe the mechanics for few of the solved problems.
These solutions mostly are not published up to these days due to variety of reasons.
These solutions are exact to the reasonable limit when one is doing simulations on a computer and using the reasonable time spent for the infinite series summation, are also the response to some aficionados of the exact solutions and to those who can not read the mathematics and like to see the curves. Unless the curves can prove more then the mathematics?
When we start to consider few spatial arrangements of averaging REVs as for the globular morphology samples as the following one -
we can ask, whether the next arrangement is good for Gauss-Ostrogradsky (GO) theorem application or not?
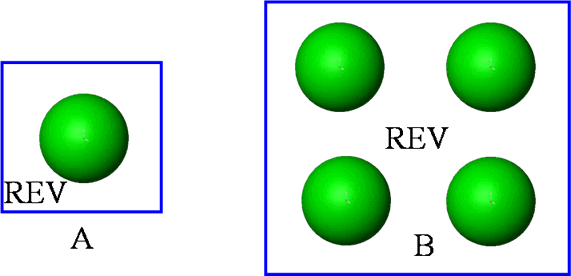
How about these 3 spatial averaging REVs? Is GO theorem applicable or not?
What about these 2 REVs? All these arrangements are legitimate and possible, or not ?
And how apply the averaging REV and make an integration ?
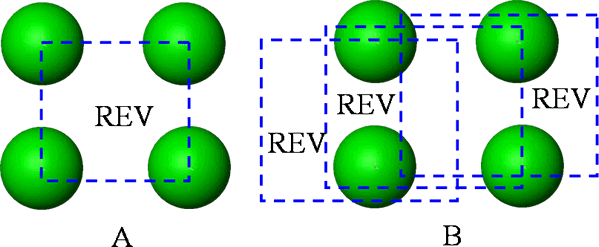
After all, we can have these REVs as possible as the others, depending on the morphology? How about the volumetric fraction value? Does it have in all of this any role ? What averaging theorem applied when the REV is as below ?
As we can guess that for the most of the above REVs the traditional homogeneous GO theorem is not applicable! So, what? One would ask.
O.K., the answer is - We need to use the Heterogeneous GO theorems - as the WSAM and their consequences. No other way so far known or invented.
Now, let's make an arrangement for the electric field applied as in the Figure below to the 3D regular medium of equal spherical particles in the matrix
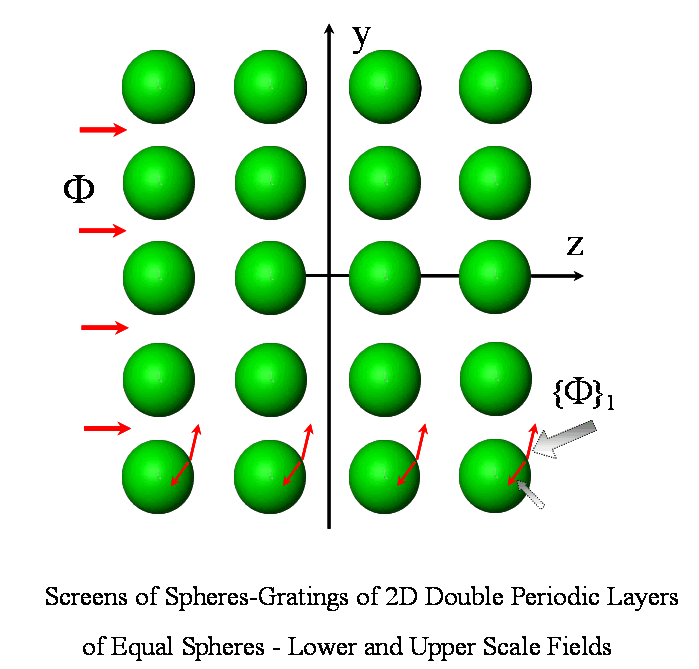
and for the inhomogeneous spatial media of the type researched and described in the following texts.
An infinite homogeneous and of inhomogeneous morphologies media containing a three-dimensional (3D) arrays of spherical particles are chosen for analysis as the globular morphology samples.
Let's consider a two-phase dielectric heterogeneous medium consisting of an
isotropic continuous (solid or fluid) matrix and an isotropic discontinuous
phase (spherical particles or pore spherical cavities). The volume fraction of
matrix, or 1st phase, is
,
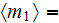
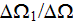the volume fraction of filler, or 2nd phase, is
,
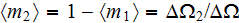where
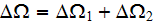is
the volume of the REV. The constant properties (phase dielectric
permittivities,
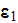and
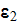), stationary (time-independent) electric potential field differential equations for
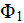and
,
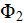the local (lower scale) phase potential variables are determined through the
3D equations, for the matrix phase in cartesian coordinates
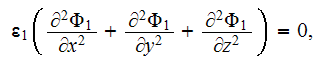(1)
and for the globular phase potential in spherical coordinates for each particle
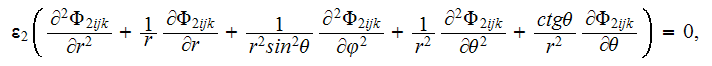(2)
where indexes
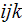designate the specific spherical particle, with the conjugate IV-th kind of
interfacial (1 - 2) potential boundary conditions between the phases
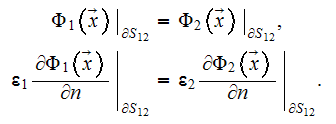(3)
No internal charges (including surficial charges) are present inside the composite medium so that the electric field is determined by the boundary conditions at the external surfaces of the sample's medium. After correct formulation of these conditions, the problem is completely stated and has a unique solution on the lower scale. It also has the the unique solution on the upper scale for the VAT upper scale equations, as long as we have solved the first scale problem. We except here the Bottom-Up sequence of scales.
The particles are arranged so that their centers lie at the nodes of a simple
cubic lattice with period
.
The potential field in this heterogeneous medium is caused by a constant
electric field
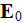prescribed
at the sample boundaries, which, due to the absence of internal sources, leads
to the equality of averaged internal electrical field
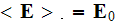(the sample boundary surface
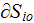cuts only through the matrix phase, Fig. 5).
When the particles have the same diameters, the result is the triple periodic structure used widely, beginning from Rayleigh's work, to evaluate the effective properties of particulate composites. We have been using that morphology for many purposes as well.
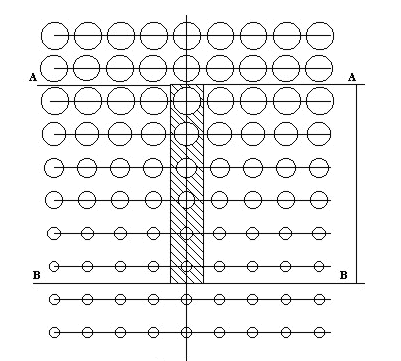
Figure 5: Model of the two-phase medium with variable volume fraction of particulate phase. Electrical field applied from the bottom.
But the most challenging morphology that was employed had the inhomogeneous spatial morphology distribution.
This model's composite medium consisted of the three regions shown in Fig.
5. The half-space lying above the A-A plane has a
volume content of the disperse phase
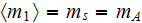and
for the half-space below the B-B plane
.
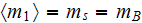To define the problem, let we have that
.
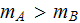The medium's third part is the composite layer between the plane boundaries
A-A and B-B containing N double periodic lattices of spheres (screens) with
changing diameters. The morphology with the changing volume fraction property
was chosen to obtain the theoretical and simulation specifics of the full
mathematical VAT statement on the upper scale.
The interface conditions (3) between both phases were used along with the external boundary condition at the B-B plane surface
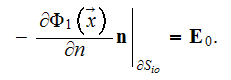
Among those available for the Upper scale non-local formulations for physical fields we had chosen to use the one with the fluctuation fields in integral terms.
The solution was sought for both scale equations. In the upper scale the problem has the only one coordinate - this is the 1D problem. The matrix phase Cartesian 1D upper scale problem was stated with the averaged (upper) scale equation
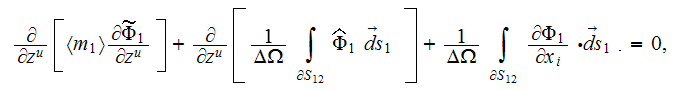(4)
which is one of the legitimate forms of the upper scale VAT equations [30,33],
plus the second (particulate) phase with constant
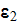upper scale equation yields the same form
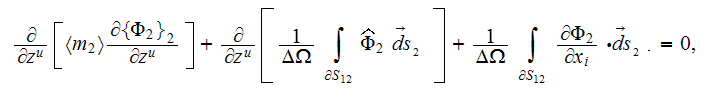(5)
where
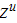is the upper scale space coordinate coinciding in direction with the lower
scale space z-axis.
The necessity of accounting for all three terms in the non-local formulation
of composite electrical bulk (mean) upper scale conductivity or permittivity
was clearly demonstrated earlier in our studies (in 90-th) while solving the
problem of heat conductivity in globular and other heterogeneous morphologies.
The exact solutions were obtained with help of complicated techniques for
solution of multi-body fields interaction (see [50,51] for globular
morphology, and [37, 46, 47, 53 ] for other morphologies with references
therein), and that is the analytical solution which was used to simulate the
numerical results of it. To demonstrate the full scale comparable input from
each of the equations three terms - the diffusive
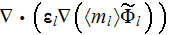term and of the two "morpho-terms"
and
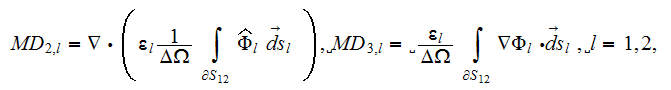
we formulate the exact two scale statement and solve the problem for the dielectric-dielectric composite medium with spherical inclusions of different diameters.
These terms are the basic source of misunderstanding and misjudgment in comparison with the classical homogeneous medium governing equations. The usual first question arises as: For what reason these additional terms should be evidently important and kept in the governing equations? Also -- How someone needs to treat these terms? And even more exact -- How to calculate these terms for a specific morphology?
Two ways to realize the solution of this problem were compared. The first is
the conventional way of replacing the actual composite medium by an equivalent
homogeneous medium with an effective dielectric permittivity coefficient,
,
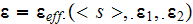assuming that one knows how to obtain or calculate it particularly. The exact
effective permittivity coefficient was obtained for this explicit lower scale
problem
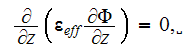
using the specifics of analytical solution for this problem.
We have to mention here that the effective coefficients directly calculated in [50,51] using the GO theorem and the straight DNM solutions based on the mathematical theory of globular morphology multiphase fields distribution developed by Kushch and other authors (see [50,51] and references therein) have the meaning for the REV's shapes and volumes that must be specifically carved, determined for homogeneous GO theorem conditions - when the only one phase is being intersected by the REV's outlined surface. That means, because of this shape and location of the REV special determination the effective coefficients calculated in [50,51] with this technique based on the Homogeneous GO theorem can not be considered as valid and are different from the real sought Upper scale effective coefficients, see the detailed explanation in -
One would to note also that the two phase lower scale exact solution for the potential does mean nothing less then that the same VAT lower scale solution in which this solution is used lately in a strictly defined mode to obtain the upper (second) scale solution of the VAT problem. The difference is that the proper Lower Scale solution averaging and data reduction give unreachable data mining and physical phenomena exposure for the one even exact solution. These effects we have already noticed in the example of the canonical superlattice problem exact solution above in -
The second way is to solve the problem using the upper scale VAT two-phase, three term integro-differential equations (4), (5). To evaluate and compare solutions of these equations with the DNM results, one needs to know the local solution characteristics, the averaged characteristics over the both phases and in this case, the additional morpho-surficial and interphase exchange terms (the second and third in the above VAT equations).
We have solved this two scale problem in both ways. This solution was obtained for the first time (in 1994-96) as for the two scale physical problem with globular morphology in these disciplines and with the accuracy unsurpassed up to these days. This accuracy is based on the analytical nature of the lower scale problems' solution.
Most of mathematics and simulation results are not published up to this time. Nevertheless, there were obtained knowledge of many outstanding problem's and the theory features.
One of the components of the second VAT equation the term
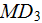is depicted in the Fig. 19b, when
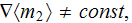
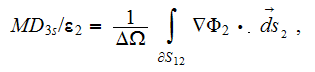
The typical behavior of the calculated according to analytical solution values
of
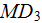is presented in Fig. 19b for
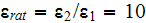and
.
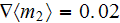It is seen from the plots that these curves calculated as the local values
oscillate periodically which is expected.
Figure 19b: The local sliding REV values of the third VAT term in the upper scale VAT equation for the particular phase in the two-scale spherical particles morphology potential problem.
The figure demonstrates behavior of this term's part that appears in the
expression for
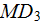(all functions are the periodic functions of the lower scale coordinate
).
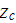Here the dashed and dot-dashed lines represent contribution of each separate
particle, solid line shows the net result. All plots are obtained with
resolution 100 points per one cell or larger.
The normalized solution of the both models (VAT and DNM) for the case of
linearly changing particulate phase fractions between A-A and B-B and with the
effective permittivity coefficients
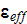and
=
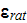0, 0.2, 1, 10, and 10,000, respectively showed (Fig. 22), practically
negligible difference (less than
)
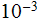supposedly because of numerical errors accumulation [50,51]). The simulation
of this problem had been done on a regular power PC in 1994-95. The coincidence
of the results of the exact calculation of two phase two equations three terms
potential VAT model (4), (5) with the exact DNM solution and with the
one-potential effective coefficient model (equation) for the heterogeneous
media with the non-constant spatial morphology clearly demonstrates the need
for using all the terms in the VAT equations. The need for the morpho-specific
terms in the upper scale equations are further demonstrated by noting that
their magnitudes are all of the same order.
,
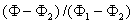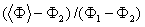
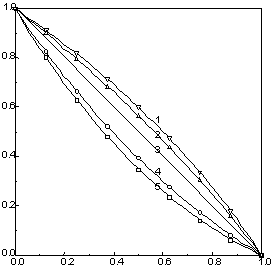
Figure 22: Comparison of the VAT three term equation particle potential, symbols, with the exact analytical solution based on the effective permittivity coefficient calculated with high accuracy.
Thus, the second term values in the VAT potential equation for the globular
phase had been found, for example, for the two sets
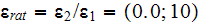of ratios of permittivity coefficients, the solution for
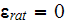calculated with
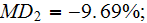and for
the value of the
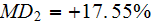of the total equation balance. The third - the morpho-exchange term
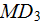constituted the
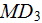values accordingly for
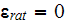the
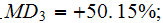and for
the value is
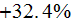as the balance portion of the upper scale VAT equation.
This picture is interesting enough because the last 2 "morpho-" terms in the
VAT equations (4,5) represent the interphase surficial transport
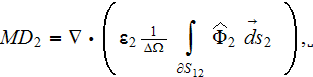and
the phase exchange potential influence -
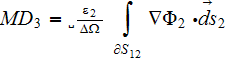on the total electrical field distribution.
Note, that these kinds of phenomena are actually known, but unreachable to simulate together directly via the homogeneous one scale models.
We need again to point out, to focus the attention of readers to this issue of ability of HSP-VAT to depict and directly involve the different physical scales and physics phenomena into the final simulating mathematical model. This feature alone should create a great deal of awareness around of this capacity which is unique at this time in mathematics, physics, and other sciences. In each and every field there are the countless problems and needs to combine and bring together the phenomena that in other ways just are being described separately, in different disciplines even, when everyone knows that those are of the same or related nature, process, etc. etc.
As, in biological and medical sciences everyone knows, speaks and study the phenomena on the surfaces of objects, cells, bacteria, (viruses !), has the intention to combine the surficial, membrane nature of phenomena on the surface, inside of the cell (bacteria, etc.), and of the bulk of the numerous colonies of cells, viruses, bacteria, etc. In Drug Delivery researchers teams used to develop the complicated physical and mathematical One Scale tools to pinpoint, to find out the place, time table and effects for unknown (or known partially) volumetrically, or molecularly delivered to the organ (tissue) drug. The surface conditions of cells, viruses, even proteins are of great importance -
And at the same time those great mathematical and software tools won't work for their intended needs as soon as the electrical fields (and other) phenomena on the surface of protein (cells), inside of the protein (cells) structure and for the huge number of closely located subjects (proteins) have being depicted (studied) with different one scale tools and models.
[1] Landauer, R. Electrical Conductivity in Inhomogeneous Media // Electrical Transport and Optical Properties of Inhomogeneous Media, edited by J.C. Garland and D.B. Tanner (New York, AIP Conf. Proc. 1978). V.40. P.2-45.
[2] Milton, G.W. Correlation of the Electromagnetic and Elastic Properties of Composites and Microgeometries Corresponding with Effective Medium Approximations//Physics and Chemistry of Porous Media, edited by D.L. Johnson and P.N. Sen (New York, AIP Conf. Proc., 1984). V.107. P.66-77.
[3] Bergman, DJ. Dielectric constant of a composite materials - problem in classical physics//Phys. Rep. 1978. V.43, N. 9. P.378-407.
[4] Meredith, R.E. and Tobias, C.W. Conduction in Heterogeneous Systems//Advances in Electrochemistry and Electrochemical Engineering V.2, edited by C.W. Tobias (New York, Intescience, 1962). P.15-47.
[5] McLachlan, D.S., Blaszkiewicz, M., and Newnham, R.E. Electrical Resistivity of Composites//J. Am. Ceram. Soc. 1990. V.73. P.2187-2203.
[6] Isichenko, M.B. Percolation, Statistical Topography, and Transport in Random Media//Rev. Mod. Physics. 1992. V. 64, N. 4. P.961-1043.
[7] Sahimi, M. Flow Phenomena in Rocks: from Continuum Models to Fractals, Percolation, Cellular Automata, and Simulated Annealing//Rev. Mod. Physics. 1993. V. 65, N. 4. P.1393-1534.
[8] Fokin, A.G. Macroscopic Conductivity of Random Inhomogeneous Media. Calculation Methods//Physics - Uspekhi. 1996. V. 39, N. 10. P.1009-1032.
[9] Dul'nev, G.N. and Zarichnyak, Yu.P. Thermal Conductivity of Mixtures and Composite Materials. Leningrad, Energiya, 1974. (in Russian).
[10] Dul'nev, G.N., Zarichnyak, Yu.P., and Novikov, V.V. Coefficients of Generalized Conductivity of Heterogeneous Systems with Chaotic Structure//Engng.-Phys. Journ. 1976. V. 31, N. 1. P.150-168 (in Russian).
[11] Cheng, H. and Torquato, S. Electric-field Fluctuations in Random Dielectric Composites//Phys. Rev. B. 1997. V. 56, N. 13. P. 8060-8068.
[12] Hilfer, R. Local porosity theory for flow in porous media//Phys. Rev. B. 1992. V. 45. P.7115-7124.
[13] Haslund, E., Hansen, B.D., Hilfer, R., and Nost, B. Measurement of local porosities and dielectric dispersion for a water-saturated porous medium//J.Appl.Phys. 1994. V.76, N. 1. P.5473-5480.
[14] L.I.Kheifets and A.V.Neimark, Multiphase Processes in Porous Media (Nadra, Moscow, 1982) (in Russian).
[25] Vinogradov, A.P. Electrodynamics of Composite Materials. (Moscow, Aditorial URSS, 2001).
[26] Vinogradov, A.P. On the Form of Constitutive Equations in Electrodynamics//Physics Uspekhi. 2002. V.172. P.363-370.
[27] Landau, L.D. and Lifshits, E.M. Electrodynamics of Continuous Media. (Oxford, Pergamon Press, 1960).
[30] Travkin, V.S. and Catton, I. Transport phenomena in heterogeneous media based on volume averaging theory// Advances in Heat Transfer. (New York, Academic Press, 2001. Vol. 34.). P.1-144.
[31] Avellaneda, M. and Torquato, S. Rigorous link between fluid permeability, electrical conductivity, and relaxation times for transport in porous media//Phys. Fluids A. 1991. V.3. P.2529-2540.
[32] Catton, I. and Travkin, V.S. Homogeneous and Non-Local Heterogeneous Transport Phenomena with VAT Application Analysis// Proc. 15th Symp. Energy Engin. Scs., Argonne National Laboratory, Conf. - 9705121, (Argonne NL, DOE, 1997). P. 48-55.
[33] Travkin, V.S. and Catton, I. Porous Media Transport Descriptions - Non-Local, Linear and Non-linear Against Effective Thermal/Fluid Properties//Advances in Colloid and Interface Science. 1998. V.76-77. P.389-443.
[34] Achdou, Y. and Avellaneda, M. Influence of pore roughness and pore-size dispersion in estimating the permeability of a porous medium from electrical measurements//Physics of Fluids A. 1992. V.4. P.2651-2673.
[35] Johnson, D.L., Koplik, J., and Dashen, R. Theory of Dynamic Permeability and Tortuosity in Fluid-Saturated Media//J. Fluid Mech. 1987. V.176. P.379-402.
[36] Sheng, P. and Zhou, M.Y. Dynamic Permeability in Porous Media//Phys. Rev. Lett. 1988. V.61. P.1591-1594.
[37] Travkin, V.S. and Catton, I. Nonlinear Effects in Multiple Regime Transport of Momentum in Longitudinal Capillary Porous Medium Morphology//J. Porous Media. 1999. V.2, N.3. P.277-294.
[46] Travkin, V.S. and Catton, I. Heat and Charge Conductivities in Superlattices - Two-Scale Measuring and Modeling//Proc. Intern. Mech. Engin. Cong. Expo. (IMECE'2001). (New York, IMECE/HTD-24260, 2001). P.1-12.
[47] Travkin, V.S., Hu, K., and Catton, I. Exact Closure of Hierarchical VAT Capillary Thermo-Convective Problem for Turbulent and Laminar Regimes//Proc. Intern. Mech. Engin. Cong. Expo. (IMECE'2001) (New York, IMECE/HTD-24261, 2001). P.1-12.
[48] Travkin, V.S., Catton, I., Hu, K., Ponomarenko, A.T., Shevchenko, V.G. Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis//Proc. ASME, AMD-233. 1999. V.233. P.21-31.
[50] Kushch, V.I. Conductivity of a Periodic Particle Composite with Transversely Isotropic Phases// Proc. R. Soc. Lond. A. 1997. V.453. P.65-76.
[51] Kushch, V.I. Microstresses and Effective Elastic Moduli of a Solid Reinforced by Periodically Distributed Spheroidal Particles//Int. J. Solids Structures. 1997. V.34, N.11. P.1353-1366.
[53] Hu, K., Travkin, V.S., and Catton, I. Two Scale Hierarchical Network Model of Heat and Momentum Transport in Porous Media//Proc. 35th Nat. Heat Trans. Conf. (2001 NHTC01-11921). (Anaheim, ASME, 2001).
[55] Zhang, X. and Stroud, D. Numerical Studies of the Nonlinear Properties of Composites//Phys. Rev. B. 1994. V.49, N.2. P.944-955.
[56] Levy, O., Bergman, D.J., and Stroud, D.G. Harmonic Generation, Induced Nonlinearity, and Optical Bistability in Nonlinear Composites//Phys. Rev. E. 1995. V.52, N.3. P.3184-3194.