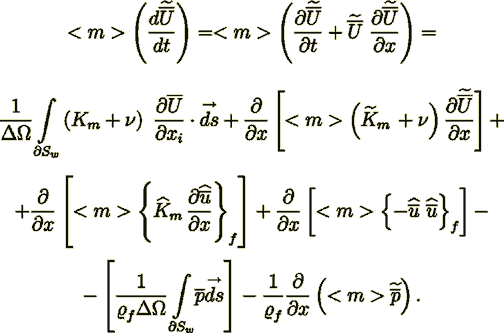One thing is obvious when effective coefficients problem arising for heterogeneous medium. Because the effective coefficients search is the problem of the Upper scale medium consideration, there is no other way to go around the VAT governing equations for formulation of the effective coefficient models.

May be the oldest problem in Fluid Mechanics is the problem of determination of the flow resistance in porous media. This is as that old task as the construction as the craft and industry exists. At the same time, the "state of the art" in here is like defending some experimental data obtained while data reduction was made with the Gauss-Ostrogradsky Theorem (GOT) used as the background tool !

Meanwhile, porous media are Heterogeneous media and by using the HSH-VAT the Momentum 1D equation in the midst of the porous medium filled channel for turbulent (as well as with nonlinear viscosity) flow of incompressible fluid based on the K-theory can be depicted in the form (Shcherban et al., 1986; Travkin and Catton, 1992, 1995a,b)

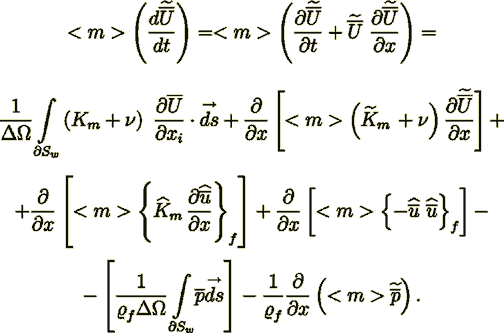(1)

A. Closure Modeling for the Integral Resistance Terms with the Simplified VAT and when the Boundary Effects are Taken as in Bulk or Neglected

The nonlocal Upper scale momentum transport equation in porous medium above has been solved so far for quite limited number of morphologies and is the subject of various simulation exercises. That is why the much simpler equations take the role.

So, believe or not, but these Arithmetical models below is the "State of the Art" in Fluid Mechanics up to now, when concerned about the practical application of flow in porous media knowledge. For near 150 years since Darcy publication of the linear dependency for pressure drop and velocity in a porous medium. There are number of models apart of HSP-VAT with differential equations for flow in porous media developed since then. Still, in practice the two or one-term r.h.s. dependency is used everywhere.

There are coefficients in the r.h.s. of these dependencies.

The matter is as usual with the proper coefficients - the flow resistance coefficients.

We did bring as like for already many years the integro-differential VAT governing equations for velocity in porous media to these simplified forms of flow resistance to connect, communicate the homogeneous Darcy and Darcy - Forchheimer dependencies to the simplified VAT equations. That was and is like making a compromise for better understanding and more introduction for usage of simplified, but still more accurate than conventional dependencies the VAT based Flow Resistance in Porous Media formulae.

Few models for momentum transport in porous media were analyzed by Travkin and Catton (1992, 1995a,b, etc.). Momentum equation for laminar regime given by Vafai and Kim (1989) for the middle part of the regenerator's layer can be written as

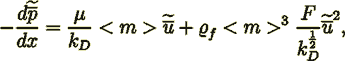(2)

while Poulikakos and Renken (1987) equation for turbulent regime looks like

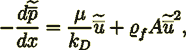(3)

as well as by Ergun (1952)

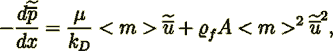(4)

and that simplified obtained using the VAT momentum equation (SVAT)

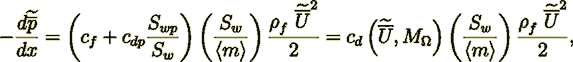(5)

where 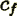is the friction factor and 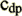the form drag, 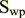is actually the cross flow form specific surface. The drag terms can be combined for simplicity into a single total drag coefficient to model the flow resistance terms in the general simplified momentum VAT equation

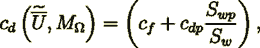(6)

where 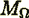is the set of porous medium morphological parameters or descriptive functions (see Shcherban et al., 1986; Travkin and Catton, 1992, 1995a). These correlations of drag resistance can be evaluated for homogeneous properties porous media by experimental relationships for pressure drop, for example, used for packed beds resistance correlations

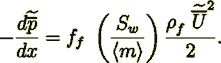(7)

The ideal one diameter parallel tubes morphology model yields the following Darcy friction coefficient models (see, for example, Schlichting, 1979)

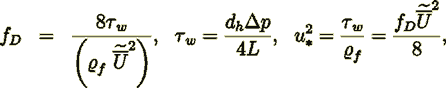(8)

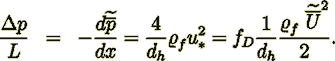(9)

In the above formulae taken that the mean velocity in a vessel (tube) where 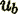is equal to the intrinsic value 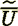averaged over the REV. A straight equal diameter tube morphology model yields the morphology function ,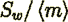

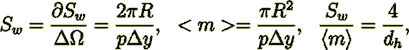(10)

or

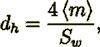(11)

and there results in the Darcy friction factor exact expression

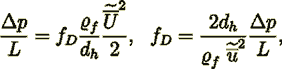(12)

from this one can easily get the Fanning friction factor for this specific morphology (using 10)

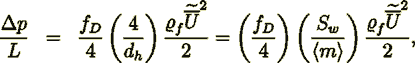(13)

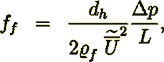(14)

from which one obtains for capillary morphology with prevailing skin friction coefficient (Travkin and Catton, 1995a)

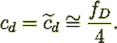(15)

This relation obviously means that the strict consecutive upscale development of porous medium capillary morphology momentum equation brings to the exact same equation (5) which was derived making "downscale" VAT analysis. The well-known friction factor for laminar flow regime in a pipe is

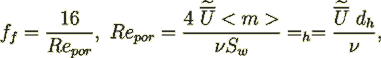(16)

while the Darcy coefficient is

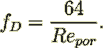(17)

It is quite relevant to compare the results of the SVAT 1D momentum equation derived directly from the general form VAT momentum equation with accounting of few simplifications to the equation derived by Blick (1966) for the straight pore with orifice medium morphology by using the conventional fluid mechanics bulk integration over the volume of interest. As one can write down the Blick's equation (5) without the two last terms which reflect the compressibility and mass force influence in the form

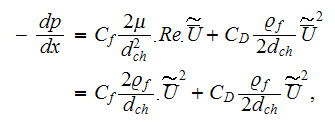(18)

where

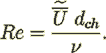
The first right hand term in this equation is exactly the Fanning friction factor for the smooth tube with diameter 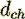written as

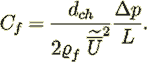
That means that the friction resistance term in the equation by Blick (1966) is exactly the term which reflects friction resistance for the like kind of morphology using the VAT equation closure procedure (Travkin and Catton 1992, 1995a,b) as given above. The friction resistance term in the SVAT equation is

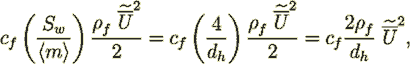(19)

so

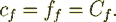
In the second form resistance term in the equation by Blick (18) the drag resistance coeffcient 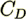is given by expression

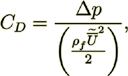(20)

which does not have any parameters describing the obstacle making that form resistance. Contrary, the VAT conventional closure suggests that this drag resistance coefficient be defined as that commonly used in fluid mechanics

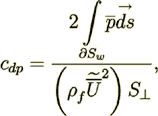(21)

with form resistance term written in the form

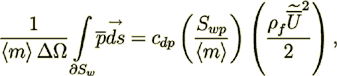(22a)

where

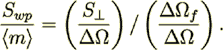(23)

The difference between both form resistance terms is merely due to interpretation of the drag resistance coefficient definition. It is easily can be shown that the morphological characteristics in the drag resistance VAT term (22a) written in the exact form for 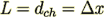(as assigned in the Blick's work)

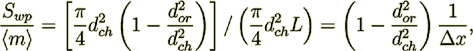(24)

where 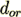is the orifice internal diameter. The last expression when the orifice internal diameter 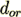is limiting to 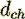, so roughness on the wall becomes vanishing when 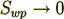, and the whole VAT form resistance term is going to zero. Meanwhile, the form resistance term derived by Blick (1966)

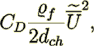(25)

should be assigned equals or close to zero, because it doesn't content any morphological parameters of obstacles, which could bring it to a zero value when physical situation is obviously trends to that value of form resistance. In another characteristic situation w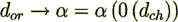hen then

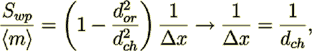
which means that the VAT drag resistance coefficient 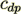and form resistance term are approaching the definition and value given in work by Blick (1966)

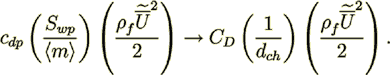(26)

The later means that an interpretation of flow resistance coefficient and term given by Blick (1966) is just the simplification that accommodate the form resistance of orifice without including of morphological characteristics of orifice itself.

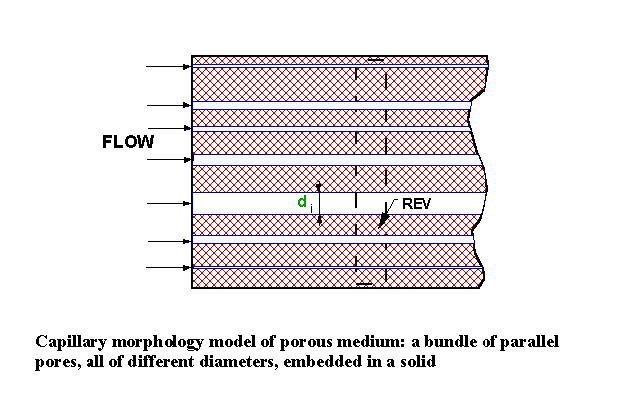
A model representing the slit morphology of a porous medium with the width equal H (and h = H/2) has defined the local friction factor 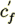on the slit wall

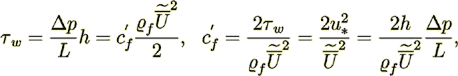(27)

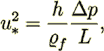(28)

where also for a regular one size slit the bulk velocity value is 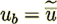The morphology ratio 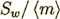for a porous medium morphology model of straight equal slits is

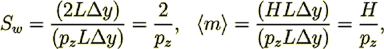(29)

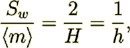(30)

where p_z is the pitch between slits in z direction.

One needs to remember that at the same time the hydraulic diameter for a slit equal

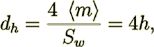(31)

but not the d_h =2h as adopted in many textbooks (Bird et al., 1960). The Fanning friction factor for this morphology yields factor as

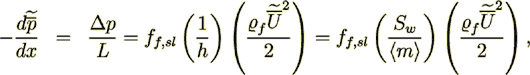
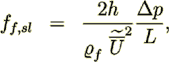(32)

identifying that for the smooth slit porous medium morphology

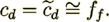(33)

Here in this subsection we should comment on the key trends and studies related to issues of effective momentum equation and effective coefficients in porous media.

As we have mentioned in our (Travkin and Catton, 1999) study the same character of our final dependencies for averaged effective momentum transport in the porous medium of Straight Parallel Pore Morphology (SPPM)

has with some of the results by Whitaker (1986). In our work the exact solution for different diameter pores medium allowed to exist the very nonlinear along with the linear and creeping flow regimes.

That does not mean that the exact effective resistance dependencies (

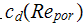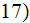
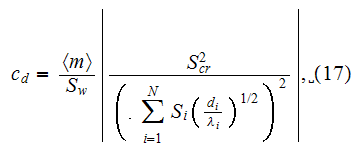
for the exact averaged (of Upper scale) momentum equation (2), (6)

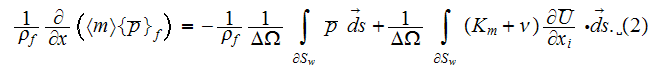
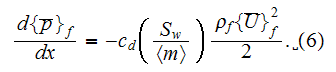
in Travkin and Catton, (1999) and the final equation for averaged pressure and velocity (C.12) (in Whitaker, 1986)

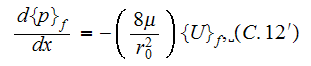
are obtained for describing the same kind of phenomena in the same kind of SPPM. The only situation with a single pore diameter in porous medium is allowed while the dependency (C.12) was derived based on linear dependencies for fluctuations of averaged variables. This condition fortunately happens in creeping flow regime.

Obviously, in the SPPM with the variety of diameters, the flow regimes and nonlinearities the linear closure methodology ascribed in work (Whitaker, 1986) is not able to solve either the Upper Scale momentum problem or to find out the effective resistance coefficients.

In the SPPM medium that had been shown in Travkin and Catton (1999)

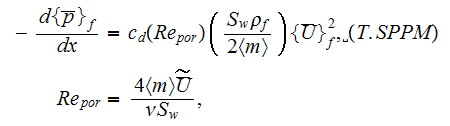
where 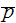and 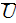- might be either of usual laminar (creeping) regime flow pattern or of turbulent regime functions. We note, that when the SPPM medium is taken as having only a single diameter pores (tubes) and only with the laminar flow then the second equation (T.SPPM) can be brought to the simplest case presented by equation

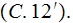
Citing here these two figures from the publication (Travkin and Catton, 1999)

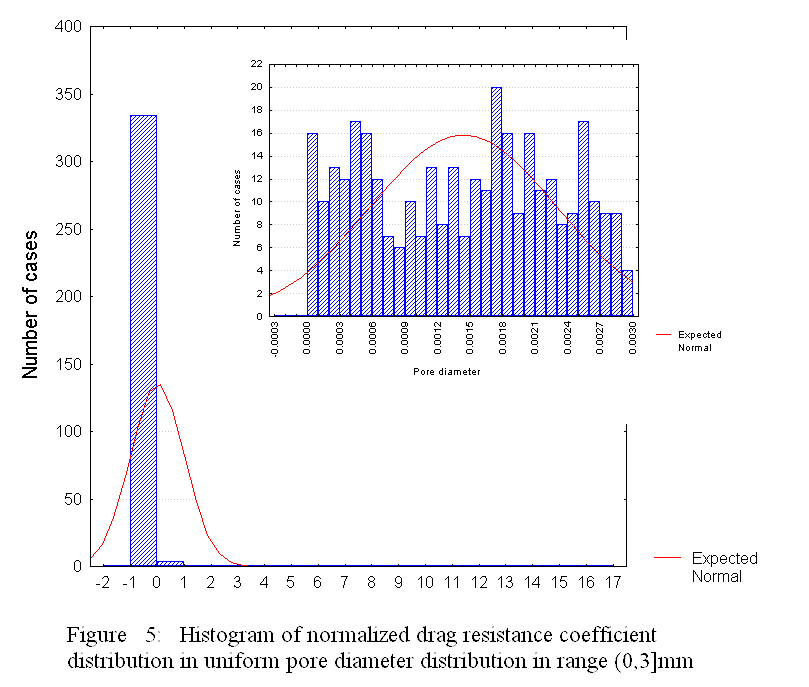
we would like to remind that no other theory or method were able to obtain this kind of effective coefficients. Coefficients that are actually exact in their Upper scale class definitions - because we have here the Upper scale exact solutions for flow in this kind of porous medium - the SPPM medium.

The second after Darcy equation in use and referring is the Forchheimer effective momentum equation for flow in porous media. In the very elaborative study by Whitaker (1996) we had got to notice the main outcome first -

is that for the exact solution of the closure problem one needs actually to solve the full scale Lower (initial homogeneous) scale mathematical statement (for laminar flow regime).

I am glad to confirm here that this statement exactly what we are saying with regard of the closure problem and not only for laminar, but other flow regimes as well, since 1980-th. Our description and basic arguments are just simpler and more straightforward then of Whitaker (1996) - we have been suggesting solving the various kinds of Lower (first) scale mathematical statement in any case, situation. After all - the both Scale Statements are directly tied, and one can not be solved without the other in the Bottom-Up sequence and in the Top-Down sequence often either.

The second issue in the study by Whitaker (1996) about the Forchheimer form of effective momentum equation is the validity of the "best" value Forchheimer coefficient.

In the page 52 we read: "The closure problem represented by Equations (4.3) has been solved by Snyder and Stewart (1966), Sorenson and Stewart (1974), Eidsath (1981), Sangani and Acrivos (1982), Zick and Homsy (1982), Edwards et al. (1991), Quintard and Whitaker (1995), and others for arrays of spheres and cylinders. For uniform arrays of spheres, the Darcy's law permeability tensor determined by Equation (4-3e) is isotropic, thus is a single distinct component that can be compared with Equation (5.6) arranged in the form

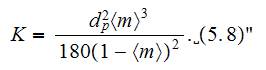
so, this is the constant permeability coefficient depending only on the morphology properties.

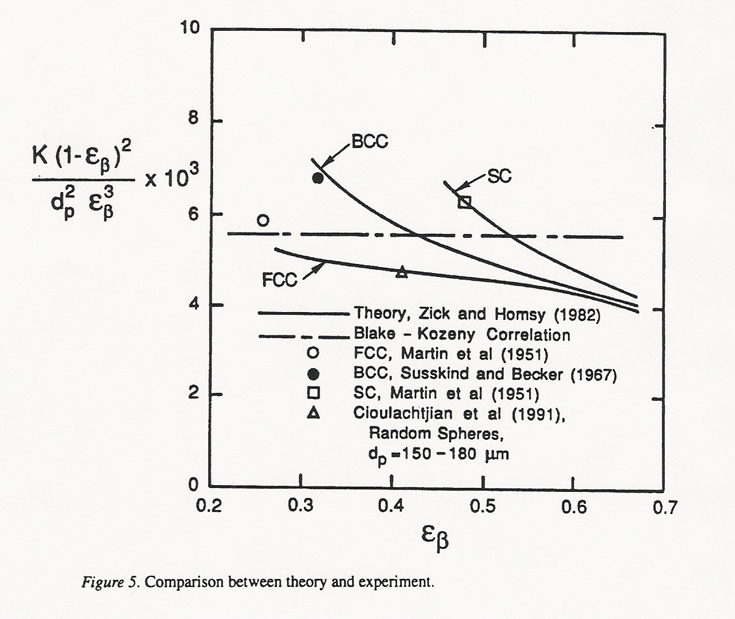
Meanwhile, we have shown in our (Travkin and Catton, 1999) that this coefficient is the function by purely solving the problem with SPPM medium. And even the nonlinear function in the case of three flow regimes or when just laminar and turbulent regimes are present in such a simple medium.

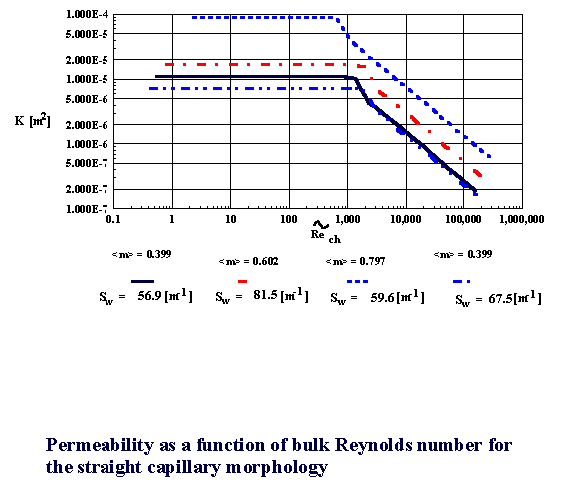
And what is more important that the experiments and modeling in mentioned studies were made with the homogeneous physics analysis and data reduction.

That alone makes the comparison the issue of verification of basic dependencies laying in the ground of corresponding theoretical studies, highly questionable.

The HSP-VAT scaling approach allowed in 90-th for the first time to get the generalized plots of flow resistance curves in which the different scale and method studies had been brought together for combined observation -

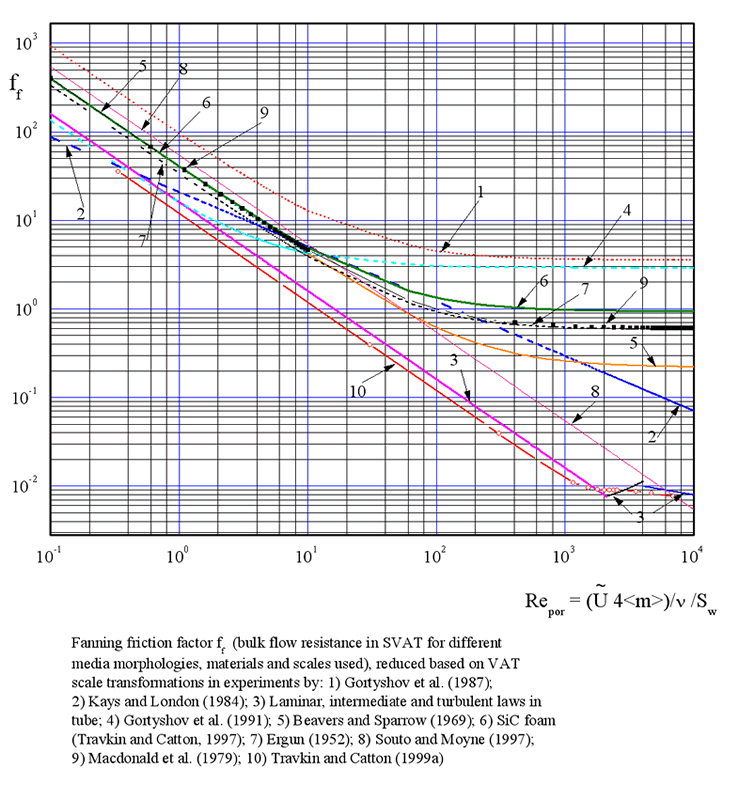
We need to say here that this kind of plots no other theory were able to produce so far for momentum transport in porous media.

Continue this topic on the Upper scale effective momentum transport coefficients we would like to say that the first case-study of initial attempt on providing the combined theoretical and experimental HSP-VAT two scale investigation of flow and heat transfer in the porous medium had been explained and has a certain level of detail in the following sub-section -