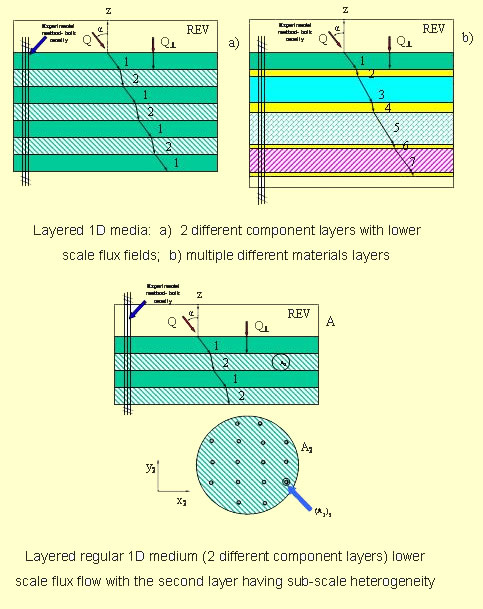
Taking the simplest combination of two phase composite of layered

or foamy, or using the foamy layers

structure, we have the averaged
temperature of that composite to be modeled as
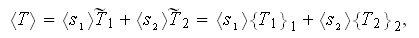
and mostly people expecting that the combined, bulk, average temperature
equation can be modeled as
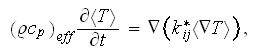
where the effective conductivity coefficient

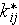 is to be found somehow based on the composite's data - as phase' properties,
morphology of composite arrangement, etc.
is to be found somehow based on the composite's data - as phase' properties,
morphology of composite arrangement, etc.
Combining the both temperature VAT equations ( if only two of phases are
present) for the simplest case of constant coefficients
(those are not such simple in a real protective shield
medium)
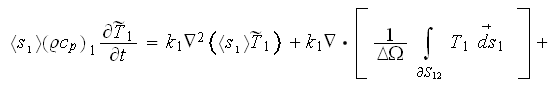
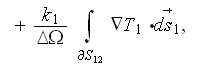
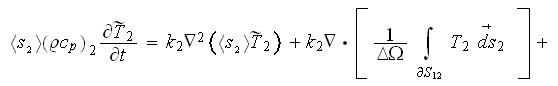
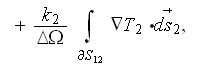
into one equation by adding one to another (when taking into account the
boundary condition of temperature fluxes equality at the interface surface -

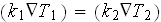 )
)
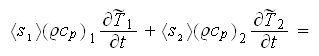
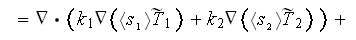
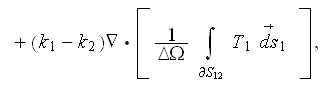
we get the strange equation which has the three different temperatures
-
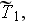

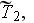 and
and

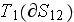 ?
?
Still our goal is not to solve this strange equation, but - to reduce the rate
of the heat flux (in another words, the overall amount of heat transported
through the wall) of the composite 1D structure - the heat transfer rate per
unit volume of protective wall per unit temperature difference

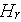
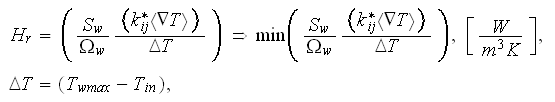
where

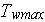 is the hot side wall temperature,
is the hot side wall temperature,

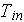 is the cold (other) side reference temperature, and of its intensity
is the cold (other) side reference temperature, and of its intensity

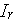
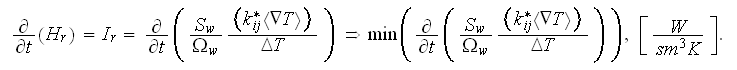
Unfortunately, we need to solve the both problems - the two-scale HSP-VAT heat conductivity problem via the composite protective wall, as well as the optimization (minimization) of the heat transfer rate problem. If we would now have the formulae for the Effective coefficient of conductivity, the both problem would be easier to solve.
That is not the case and because of this the optimization (minimization) of the heat transfer rate problem is continue to be the "UNSOLVED PROBLEM" now even for the constant coefficients statement. The few reasons for difficulties are:
a) this is the two-scale HSP-VAT problem, no matter what people ARE SOLVING AND SAYING RIGHT NOW;
b) this is the distributed parameters optimization problem with the aggravated mathematical statement of the Two-Scale problem, and not a single of these optimization problems was solved up to these days;
c) this is the problem with the Heterogeneous Transient two phase effective coefficients.
To find out the effective coefficient of conductivity for the composite
two-phase medium as for the phase constand coefficients
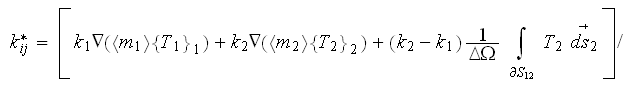
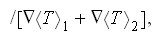
one still needs to solve the HSP-VAT two-scale problem first. The nonlinear heat conductivity HSP-VAT problem in a two-phase composite involves the definition for the effective coefficient of conductivity
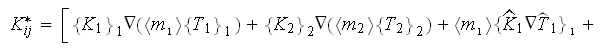
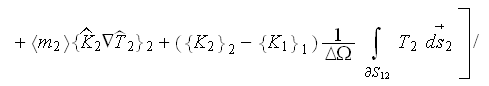
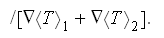
And by the way, in all these developments the transient effective coeficients
The problem is with the left hand side governing equation forms, they are not identical, they need to be matched one to another.
So, the heat transfer rate
As we have shown in the
- "When the 2x2 is not
going to be 4 - What to do?".
the problem which itself presents the basis for design of protective thermal
barrier and which was considered during at least the last 70-80 years as the one that had been solved finally and
completely, and in a linear form as being solved exactly analytically, but in
reality it was not.
It even can not be solved with the one scale homogeneous
physics mathematical statement, because
it has the discrepancy features those can not
be explained within the one scale mathematical statement, for example,
according to homogeneous statement the equality for heat fluxes in each of the
layers

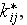

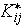 are still not exact match to the one temperature
are still not exact match to the one temperature 
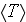 equation
equation
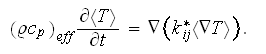

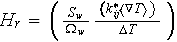 minimization brings in the complicated two-phase coefficient of conductivity
assessment. We have done this kind of assessment for the semiconductor heat
sink two-scale solution and optimization see in -
minimization brings in the complicated two-phase coefficient of conductivity
assessment. We have done this kind of assessment for the semiconductor heat
sink two-scale solution and optimization see in -
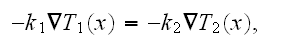
should be preserved with the temperature fields found in the solution for the averaged fluxes
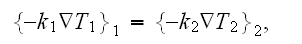
as soon as in homogeneous physics
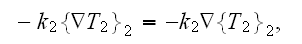
then should be
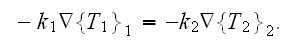
But this equality does not happen, so why? and What does it mean?
Recently this problem has been solved as the two-scale HSP-VAT mathematical formulation. What is interesting is that it can be solved for a linear case (with the constant phase coefficients) in the strict analytical form, giving no chances for conventional treatment of this problem.
This also means that the thermal barrier (shield) problem design - on the each scale level, can not be found in brackets of the one scale treatment. The one scale design of the two- or three scale problem is not a valid design!
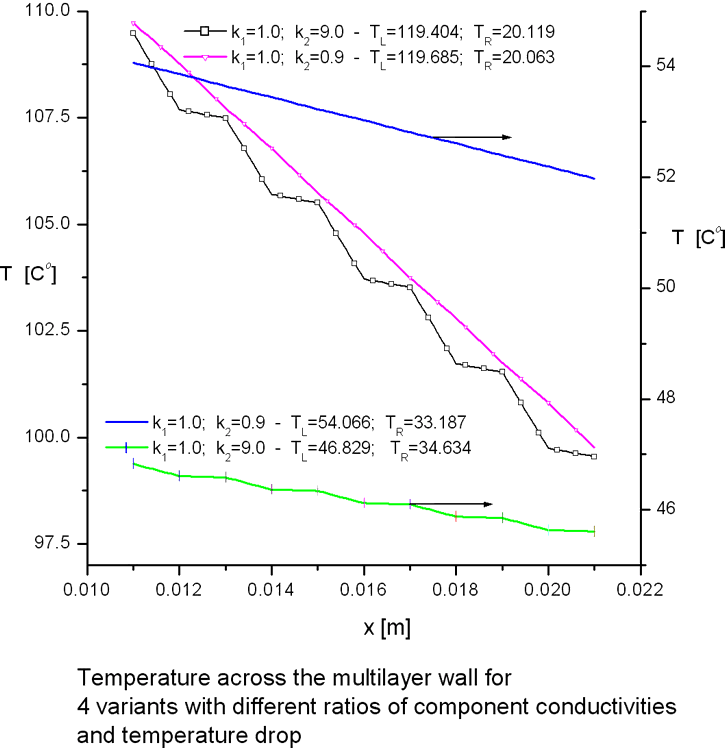
With this solution in mind it is interesting observing the properties of the found effective coefficient of conductivity.
If anyone asked himself (herself) - Why the problem with the starting
conductivity coefficients ratio as high as

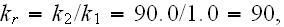 with the good intention to decrease the total effective wall's thermal
conductivity coefficient playing down the high value of one of the phase
involved
with the good intention to decrease the total effective wall's thermal
conductivity coefficient playing down the high value of one of the phase
involved

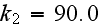 to
to

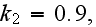 or for two orders of magnitude lower, and then still getting the result for the
effective wall coefficient decreasing to a value only less than a two times
smaller?
or for two orders of magnitude lower, and then still getting the result for the
effective wall coefficient decreasing to a value only less than a two times
smaller?
That's seems illogical ? What is the physical, and mathematical explanation of
this fact? The problem is the straightforward one, no nonlinearity, no hidden
difficulties in the solution, so why the final change for the

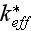 is so small? Or, better to say - Why the starting effective coefficient is so low?
is so small? Or, better to say - Why the starting effective coefficient is so low?
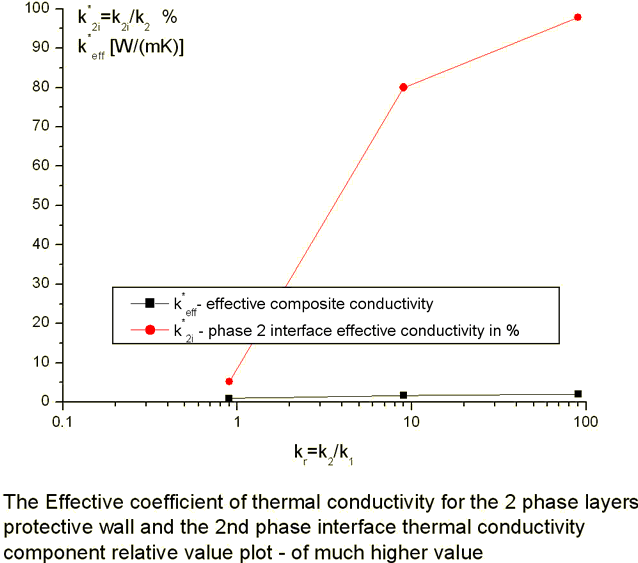
No answer to this question can be found in textbooks.
On the other hand - that is definitely more close to explanation when someone would watch the plots like this one
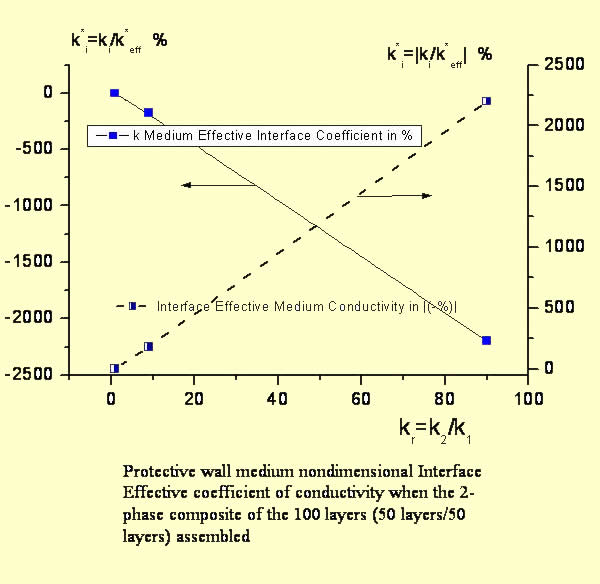
where based on HSP-VAT calculations the cause we have shown is of that as soon as there is some interface physical effect for the transport - which we call the interface effective (collective if you mind) conductivity coefficient which is actually going down and down in negative to balance in its specific way - by -177.8% of the final effective conductivity magnitude (for example, for the pair k2=9.0, k1=1.0), then the quantity of effective conductivity goes to the merely one quantity which is close to the lowest conductivity phase value.
See more explanations and detail in - "When the 2x2 is not going to be 4 - What to do?".

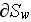 - internal surface in the REV
[
- internal surface in the REV
[
 ]
]

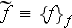 - averaged over
- averaged over

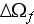 value
value

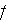 - intrinsic averaged variable
- intrinsic averaged variable

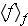 - value f, averaged over
- value f, averaged over

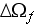 in a REV - phase averaged variable
in a REV - phase averaged variable

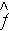 - morpho-fluctuation value of
- morpho-fluctuation value of

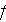 in a
in a

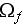

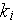 - thermal conductivity
[
- thermal conductivity
[
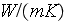 ]
]

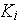 - nonlinear thermal conductivity
[
- nonlinear thermal conductivity
[
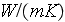 ]
]

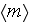 - averaged porosity [-]
- averaged porosity [-]

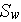 - specific interface surface of heterogeneous medium
- specific interface surface of heterogeneous medium

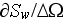 [
[
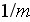 ]
]

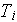 - phase temperature
- phase temperature

![$[K]$](design1com__50.png)

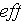 - effective
- effective

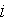 - component of vector variable; or species or pore type
- component of vector variable; or species or pore type

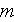 - scale value or medium
- scale value or medium

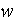 - wall
- wall

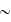 -
value in phase averaged over the REV
-
value in phase averaged over the REV

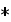 -equilibrium values at the assigned surface or complex conjugate variable
-equilibrium values at the assigned surface or complex conjugate variable

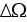 -
representative elementary volume (REV)
-
representative elementary volume (REV)

![$[m^{3}]$](design1com__58.png)

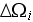 - phase volume in a REV
- phase volume in a REV

![$[m_{3}]$](design1com__60.png)

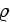 - density
[
- density
[
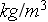 ];
also
];
also

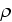 - electric charge density
[C/m
- electric charge density
[C/m
 ]
]
![]()