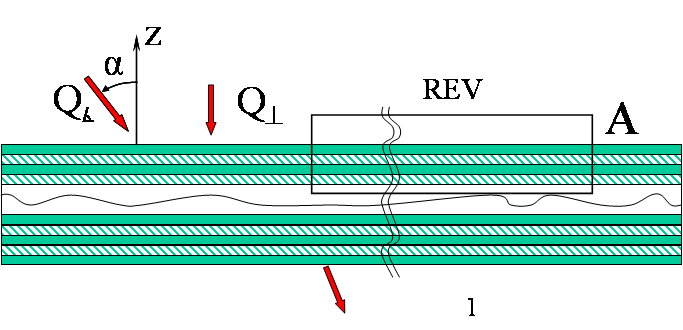
This is the well known in many physical sciences problem, and in acoustics definitely.

The homogeneous Lower scale solution and some one scale analysis of the problem has done in all the textbooks, while we will follow the text for this problem Lower scale solution - homogeneous media solution, given by Brekhovskikh. This book also is well known in English. There are few books in English on the topic by this author and his co-authors.
Telling that, we won't put a lot of introductory text for the lower scale homogeneous statement, because it is given in many books and papers and everybody familiar with the problem can refresh the conventional statement and solution looking into the one of available shelf books. We won't be able also to give much of the derivation procedures and mathematics regarding the Upper scale Ht Acoustics equations. Some exposition had taken place in the published pieces cited in the introductory subsection for Ht Electrodynamics -
Let we use the Figure 3.2 (from one of Brekhovskikh books) - where shown the (n-1) layers between the
half-spaces, starting as from below at

 (while could be and at any other height) and having the incidental acoustical
wave from above under the angle
(while could be and at any other height) and having the incidental acoustical
wave from above under the angle

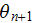
As usual in acoustics for many texts here

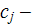 is the speed of the sound in each medium,
is the speed of the sound in each medium,

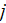 is the layer's ordinal number;
is the layer's ordinal number;

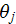 - is using for the angle of incidence of the sound wave in each layer ,
- is using for the angle of incidence of the sound wave in each layer ,

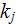 - is the wave number,
- is the wave number,

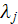 - is the wave length
- is the wave length
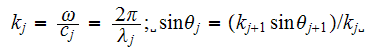
This is the often used and well accepted assumption about interface surface. For this particular problem and its statement it brings simplification into the both scales treatment.
The HSP-VAT upper scale acoustic equation in the phase one simplifies for the general 2D situation (y,z), here we took advantage of more
vivid compliance with the Cartesian 3D figure that we used to apply, to
the following one
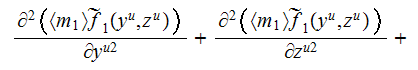
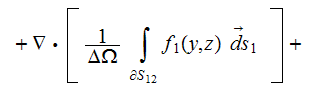
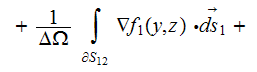
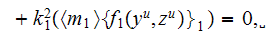
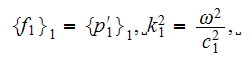
when the interface is completely rigid.
The Lower scale acoustics equation in the phase one is as
usually
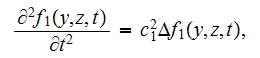
or in the harmonic form 2DL
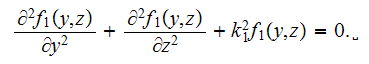
This equation, while a 2D incident field will impact the superlattice
at

 or at
or at

when used the statement set-up as in the Brekhovskikh's book, then it becomes in the Upper scale
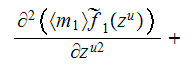
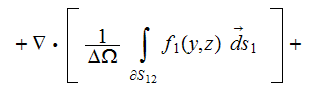
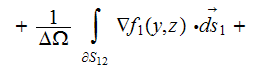
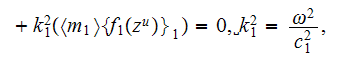
or when strictly vertical incident field applied then
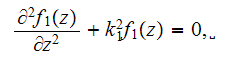
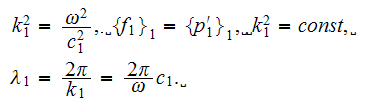
These above two averaged acoustics equations are the exact copies of the simple linear EM Upper Scale wave propagation equations from -
The difference is that for the EM fields equations used

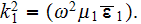
These equations have been studied without the last (source) term for the globular morphologies by me and V.Kushch in 94-96, and we get many results (most are unpublushed), as, for example:
1) Has been developed the Simulation Averaging Techniques (SAT) for the analytical solution for each term on the Upper Scale and numerical calculation of those terms on the Upper Scale.
2) Has been developed the mathematics of analytical averaging of the fields;
3) Has been solved "exactly" (as allowed the computer power at that time) - few two scales conductivity and laminar flow problems for the two phase heterogeneous and porous media with globular morphology fillers;
4) Has been developed the methodology for verification of the WSAM theorem by analytical modeling with then simulated problems using the DMM-DNM; etc.
See some outcomes also in the section on Ht Electrodynamics -
We would give here few outstanding features from the Two Scale solution for the conventional one scale known and studied by anyone involved in the field problem of acoustic wave incidental upon the multilayer medium consisting of two or more phases of alternating layers- the acoustic wave propagation in superlattices.
Actually, we have found more than one method of solving this famous problem as the two scale Heterogeneous Acoustics problem. One of the methods is completely analytical - and this is the second of generally known analytical methods for the two scale VAT problems for superlattices.
Another one was developed for the steady-state thermal (diffusion, electrical) conductivity problem for the superlattice in-cross distribution of fields -
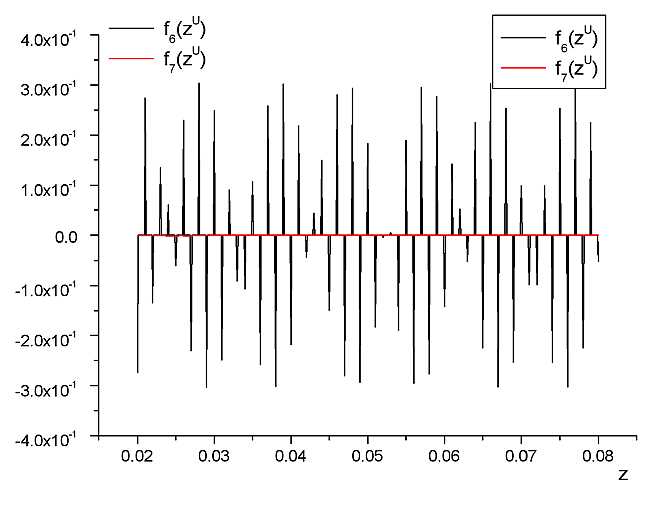
The Upper Non-Local scale solution of this problem would be nice to illustrate with the few figures related to the Upper scale functions.
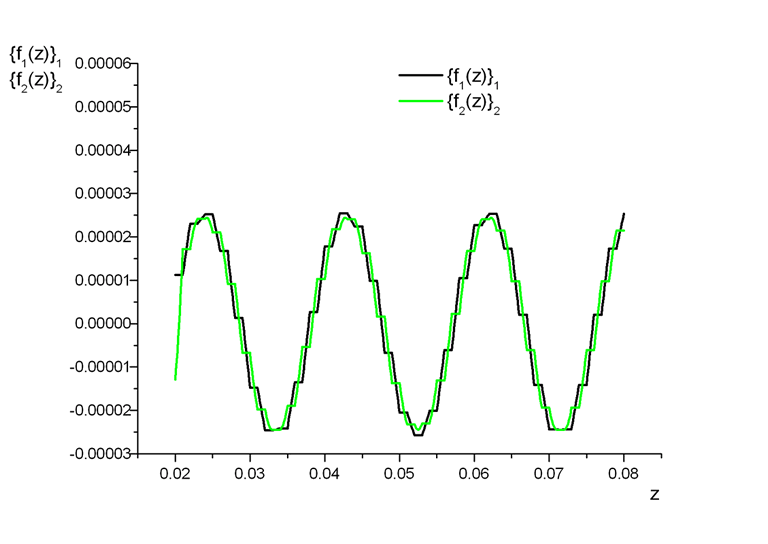
The Upper scale (averaged) wave-derived functions in both phases. The wave incident is from the right (top in the problem's Figure 3.2 above).
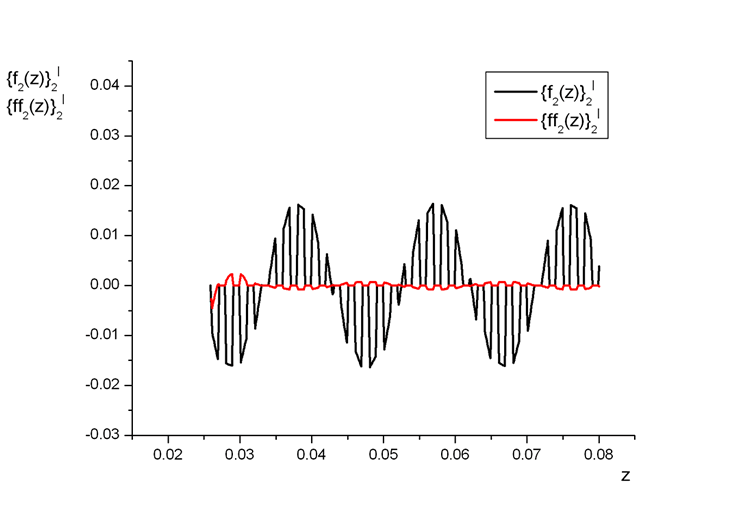
Derivatives of the two wave-derived functions in phase two on the Upper Scale.
The plots of function in the presented on the following two figures are pretty much common when the wave length gets in the range comparable to the width of the separate layer in the pack.
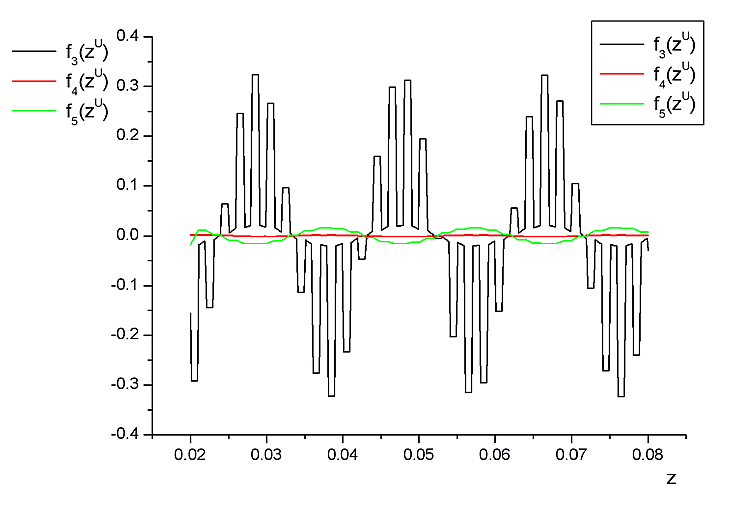
Few outstanding features that presented in these function plots have been used for the Upper scale acoustics equations solution for layered (superlattice) morphologies.
As long as this is the fundamental decent problem, problem that communicates with and has impact for many technologies - so far with published by other authors results pertaining to only the lower scale local aspects of homogeneous acoustic wave propagation (no matter what authors saying), we continue to study some aspects of it and will be uploading data and interesting summaries for education and comparison with the homogeneous acoustics outcomes.
Brekhovskikh, L.M., Waves in Layered Media, Moscow, Nauka, (1973), in Russian.
Brekhovskikh, L.M. and Godin, O.A., Acoustics of Layered Media I. Plane and Quasi-Plane Waves, Wave Phenomena, Vol. 5, Springer-Verlag, Berlin, (1990).