Accomplishments - Only the HSP-VAT Tools Have Made these Problems Solved
Will be updated for the time of 2002-2014 with the
Hierarchical Polyphase Polyscale Paradigm Concepts,
HSP that stands for Open End Physics
RESEARCH ACCOMPLISHMENTS IN THE DEVELOPMENT OF
HIERARCHICAL MULTI-SCALE PHYSICS VOLUME AVERAGING THEORY (HSP-VAT) AND ITS
APPLICATIONS IN PHYSICS AND TECHNOLOGIES (1979-2007)
Presented below the list of research and development accomplishments is the result of my studies and reflecting my collaborations with people from many countries. During the last twenty-something years focused primarily on the determination of fundamentals of scaled hierarchical theory in different physical disciplines. The reason for this is the ultimate role which plays in physics the mathematical theorems of Gauss-Ostrogradsky type. These theorems are used to lay the foundation for every physical field mathematical modeling capabilities. That is why the heterogeneous analogs of these theorems should be used for mathematical description of heterogeneous and hierarchical scaled media and phenomena in these media.
All of the results concerned and described below were obtained using the Hierarchical Scaled Physics-Volume Averaging Theory (HSP-VAT) and to be believed are hardly achievable or pointless when other theories applied.
THERMOPHYSICS AND MASS TRANSFER
Conductive and Convective Thermal Transport
Turbulent and non-linear transport of heat and mass mathematical models development was the major breakthrough in this field. Methods involving the strict analytical or statistical description of the morphological aspects of heterogeneous two- and three-phase media are employed in the theory. Essentially the influence of structural morphology is determined by utilizing various analytical (statistical), numerical methods for closure and solution. Models are developed, beginning at the pore-scale level. Boundary and interface conditions are incorporated at various scales leading to descriptions of transport in porous media.
Firstly solved the "classical" textbook presented conductive heat transport problems for layered (superlattice) problems on the two (2) physical scales. Shown incompleteness and insufficiency of the conventional one scale solutions.
Globular porous medium morphology (spherical particles) conductivity problem was solved exactly as the two scale problem for the first time.
Single-Phase Flow in Porous Media
Transport models for forced, single phase fluid nonlinear and turbulent convection were extended for non-uniformly and randomly structured highly porous media. Special attention was given to the evaluation of two-temperature energy and two-concentration solute transport models while emphasizing local solid phase morphology. The random characteristics of the porous medium were simulated by the use of regular and unspecified statistical, pre-assigned solid phase morphologies. Throughout the course of model development and evaluation, numerous issues consistently reappeared. These issues were the impact of medium morphology upon transport process characteristics, methods for the closure of the mathematical equations, the incorporation of specifics of turbulent mass, momentum and heat transfer process descriptions into the models, the expression of physically accurate boundary conditions, and coupled transport modes in highly porous media.
Has been solved the problem for the stochastic distribution straight pore porous medium laminar and turbulent flow and heat transfer on the two (2) scales exactly for the first time. This problem is given in each textbook on porous medium transport, but never was solved correctly even for laminar flow.
Has been solved exactly the few laminar problems for globular (spherical particles) porous medium morphologies on both scales.
Development of Second-Kind Turbulent Transport Models in Porous Media: Heat Transfer Studies
Special models that correctly account for the medium morphology characteristics were developed to describe turbulent flow and diffusion of admixtures and energy processes in a highly porous medium. Equation sets for turbulent filtration and two-temperature or two-concentration diffusion were obtained for non-isotropic porous media with interface exchange and microroughness based on second order turbulence models. The equations having been developed with an advanced averaging technique and a hierarchical modeling methodology involving fully turbulent models capable of accommodating Reynolds stresses and fluxes in the space of every pore. The equations for both developed flow and diffusive processes in a random, highly porous medium were obtained.
Additionally, the statistical and numerical methodology was developed both to close the equation set and to treat the fluctuation terms for various assigned random porous morphologies. The closure issue is important because the few authors who have correctly derived averaged governing equation set seven for laminar regime have not developed closure methods for the equations, except for the case of linear approximation for fluctuation variables.
The few turbulent heat and momentum transport problems have been solved for heterogeneous media exactly (developed the scaled closure and simulation).
The Influence of Medium Morphology on Transfer Process Characteristics
A nonlinear models for two-temperature heat and momentum turbulent transport require the evaluation of additional terms and transport coefficient models. This approach required that the coefficients in the equations, as well as the form of the equations themselves, be consistent to accurately model the processes and morphology of the porous medium. A first approximation for the coefficients, e.g. drag resistance or heat transfer, was obtained from experimentally determined coefficient correlations. Existing models for variable morphology functions such as porosity and specific surface, were used to obtain comparisons with other works in a relatively high Reynolds number range.
All the coefficient models used and discussed in the study were strictly connected to assumed (or admitted) porous medium morphology models, meaning that the coefficient values are determined in a manner consistent with the selected geometry. Comparison of modeling results occasionally posed difficulty not only because other models utilized different mathematical treatments, but also because results for such specific treatments of the medium morphology were rarely obtained by other authors.
The two-temperature models were compared with a one-temperature model using thermal diffusivity coefficients and effective coefficients from various authors. The calculated pressure drop showed very good agreement with experiment for a porous structure of spherical beads. The transport equations were sensitive to the types of morphology assumed and the descriptive ability of the transport coefficients used. It was shown for the case of the overall drag coefficient that morphology assumptions implicit in the coefficient models make themselves known by the regimes in which the models predict. A multiple contribution formulation for the overall drag coefficient resolved order of magnitude discrepancies among globular and capillary tube morphology models by modifying the morphology assumption to that of a bi-porous medium.
The form of the local thermal equilibrium statement used, however, proved somewhat insensitive to the effective conductivity model used and displayed excellent agreement with a weighted temperature from a two-temperature energy statement at high porosity, mediocre agreement at moderate void fraction. The effective thermal conductivity model presented shows minor sensitivity to fluid phase contributions while emphasizing those of the solid structure for the high conductivity solid phase (steel). Turbulent eddy conduction is observed to have increased impact within the two-temperature energy model at high void-fractions.
Numerical evaluations of the models show distinct differences in the overall drag coefficient among the straight capillary and globular models for both the regular and simple cubic morphologies. Unsurprisingly, the Nikuradze formulae (capillary models) were shown to predict overall drag coefficients approximately two orders of magnitude below the globular model values for identical local void fraction and specific surface in the considered cases.
Radiative Transport in Porous and Heterogeneous Media
The mathematical basis of radiative transport in heterogeneous media was rigorously formulated for the first time using methods of hierarchical VAT description. The interface phenomena become recognized and explored in this way which gives possibility of comprising an optical and energy transport in a more strict interacting mode. Terms used in present formulations some of those were intuitively introduces before are explained and made up the more general and correct description. It was shown why many attempts at generalization of the transport equations are inadequate. As a part of a new set of equations for electromagnetic and spectral intensity fields, the diffusion approximation was extended.
CLOSURE THEORIES IN HSP-VAT
Developed the hierarchical media governing equations exact closure and solution for the VAT specific situation of capillary and globular two-scale problems. Demonstrated its availability for important applications such as membrane transport, etc. It had been proven that the generalized momentum and scalar transport equations correctly involve additional terms which quantify the influence of the medium irregularity. Theoretical forms of these additional terms, derived from application of the closure methodology, were reviewed for both one- and two-dimensional cases in a porous medium morphology consisting of specified, stationary distributions of a polydisperse systems of straight, non-intersecting pores and for globular morphologies of equal and spatially changing globular diameters.
Outstanding features of these closure models for additional integral terms in the equations of flow and heat transfer were made obvious. It was shown that the approach taken to close the integral resistance terms in the momentum equation for a regular structure can be obtained in a way that allows the second order terms for the laminar and turbulent regimes to occur naturally. These terms were interpreted to be analogous to the Darcy or Forchheimer terms for different flow regimes.
Later on, the equations for developed flow and diffusive processes in a random, highly porous medium were revisited with the added complexity of the greatly needed statistical and numerical methodology to treat the fluctuation terms which arise for various assigned random porous morphologies. Once prescribed, the statistical nature of the capillary or globular porous medium morphology gives the basis for transforming the integro-differential transport equations into differential equations with probability density functions governing their stochastic coefficients and source terms.
Various descriptions of the porous medium's structural morphology determine the importance of these terms and the range of application of the closure schemes. Several different closure models for these terms for some uniform, nonuniform, non-isotropic and specifically random non-isotropic highly porous layers were reported. The numerical simulation includes several approaches to conditional closure modeling over the rough surfaces of pores and volume morpho-convectional dispersion and morpho-diffusive dispersion of momentum, substance or energy in a randomly nonhomogeneous medium.
The proper form of the governing equations has been a source of frequent discord among various researchers. The form of the Darcy term as well as the quadratic term was shown to depend directly on the assumed version of the convective and diffusion terms. More importantly, both diffusion (Brinkman) and drag resistance terms in the final forms of the flow equations were proven to be directly connected. These relations follow naturally from the closure process. The resulting necessity for transport coefficient models for forced, single phase fluid convection led to their development for non-uniformly and randomly structured highly porous media.
Though several different closure models for the source terms for uniform, non-uniform, non-isotropic and specifically random non-isotropic highly porous layers had been extensively developed and tested, the unique situations arising from attempting to describe processes occurring in irregular or random morphologies. It was suggested based on the VAT statements analysis that a medium's irregularities may be used to control and enhance the desired transport properties. A way to determine and control momentum transport through a capillary nonintersecting medium by altering its morphometric characteristics was given as an example of the process.
A common occurrence in porous media modeling is the inverse problem, requiring the calculation of many coefficients. As an approach to inverse problem solution for a fundamental morphology class, exact closure procedures were derived from a capillary type morphology description at the pore scale. The elementary macro-volume morphologies initially considered were systems of straight-equivalent channels with anisotropic features and random morphology fluctuations.
The differences among the modeling results, and their significance to the closure scheme, were increased by introducing specific kinds of nonregularity to the medium's morphology. In some cases, large deviations in the overall results were obtained by merely allowing small morphology nonregularities. Numerical simulation extracted important physical behavior from the morphology model by showing the influence of and by suggesting correlations for both weak and sufficiently large deviations on transport in porous medium morphologies. It was shown numerically that slight manipulations of the morphology descriptors can create large fluctuations in transport parameter values, signifying the potential for modeling errors if particular features of the morphology are neglected.
Important physical behavior was extracted from the morphology model by illustrating how hydrodynamic flow regime considerations also significantly effect the transport parameter values. A method for closure of the morpho-fluctuation terms in the governing transport equations is outlined by the use of ensemble averaging over potential configurations for the prescribed morphology. The outlined method allows either the determination of expected transport parameters given a description of the porous medium, and may also suggest qualities of the porous medium given description of the desired transport parameters.
Applying VAT to pore level transport in straight capillaries results in two sets of scale governing equations. One scale is the upper scale VAT equations which describe volumetric (ensemble) properties for flow and heat transfer in porous media. The other scale is lower scale laminar and turbulent transport equations which are for flow and heat transport in each straight pore capillary. There were exact calculations for demonstration how such a tremendous importance and unresolved in past issues as simultaneous stochastic orientation and diameter of the pores are incorporated in the upper scale experimental and simulation procedures. There were estimated the final statistics of VAT variables and connected those to experimentally measured bulk correlations for characteristics in porous layers and membranes.
FLUID MECHANICS
Basic governing equations for nonlinear and turbulent transport in porous media were developed. Developed - turbulent fluctuations simulation equations averaging; the multiscale hierarchical description of transport equations with nonlinear and turbulent regimes between two conjugate porous media. Were developed closure of VAT two scale problems via direct micro-modeling in the lower scale environment. First developed - methods of closure in globular morphology problems and developed method of verification of the averaging theorem using the direct micro-scale modeling.
New type of 1D momentum transport law in the porous medium resembling the Poiseuille's law was formulated. Non-Newtonian fluid flow in micropores and governing equations for these non-linear problems, like averaging, fine scale phenomena and pore roughness influence.
Among the many possible models for turbulent momentum in porous media, the so-called k-epsilon turbulence models are considered to be appropriate and taken as an example for the lowest level of hierarchical modeling. The fluctuations produced by the porous medium heterogeneity and wall roughness contribute to the overall transport processes and to the governing scalar fluctuation equations, the Reynolds stress equation, the turbulent kinetic energy (TKE) and the dissipation rate of TKE. These equations must be treated along with other phenomenological dependencies. In view of the theoretical importance to turbulent transport in porous media, incompressible turbulent flow within porous media was modeled using the proper averaging of the transport equations for the turbulent kinetic energy and its dissipation rate. The closures for more simple models of these equations were obtained for a few morphologies. The averaging of these equations is based on strict principles developed for application of volume averaging theory (VAT). A variety of closure alternatives were considered for application to the VAT turbulent kinetic energy and VAT dissipation rate of TKE resulting in a set of simulation equations.
Simulation of Turbulent Momentum, Heat and Mass Transfer in Rough Channels and over Rough Surfaces
A VAT approach was used to develop turbulent flow and heat transport models on the primary level of the hierarchy - on the pore scale level. It had been shown that the flow resistance and heat transfer in a rough channel or pipe, as well as a fully occupied medium, can be properly predicted using the technique of averaging the transport equations over the REV. Random characteristics of the porous medium were simulated by the use of regular and unspecified statistical, pre-assigned solid phase morphologies. An overall coefficient of drag resistance was determined by implementing a multiple-regime superposition approach. The superposition approach was tested for the case of a rough channel with included spherical obstructions. Coefficient models were evaluated using the governing averaged transport equations set and solved numerically.
The transport model and the similarity assumptions were verified with smooth wall calculations by showing that the computed friction factors and velocity profiles have excellent agreement with commonly accepted correlations. Reasonable predictions of friction factors for tubes roughened by rectangular and semi-circular ribs were made with the proposed drag resistance model for two-dimensional ribs that is based mainly on the effect of the local flow deflection in front of the rib. Insufficient experimental data were available for the verification of other geometries (triangular, trapezoid). It is postulated that the predictions for these geometries are also reasonable
because the model worked well for "extreme" geometries (rectangular and semi-circular).
Extreme Transitions in Porous Channel
It is the basic requirement for the transport models that the models' results converge to physical results for the extreme cases where the governing parameters approach to their limits. A mathematical model that predicts laminar and turbulent flow and heat transfer for plane two-dimensional channel flow filled with a regular porous medium in the limit as porosity approaches unity or zero was developed. For channel flow in porous media, independent of the model used, the model results should approach the theoretical solution of a regular channel in the limiting cases.
The development was carried out in two steps. The first is based on partial differential equations for momentum and energy conservation in the fluid and solid phases (two temperatures) in the channel derived from volume averaging theory (VAT) for a medium with a continuously changing of porosity and specific surface area. The second is to make changes to the porous layer morphology on the surfaces of the channel. After comparing with some prominent work presented in the literature and applying the closure model to some general morphology structures, it is proved that both the transport model and closure scheme are consistent when extremes of porosity were approached. Some numerical results that illustrate what occurs when the porosity approaches unity or the porosity approaches zero show that the features of momentum in the channel are smoothly converge to the transport characteristics of a plane channel.
OPTIMIZATION THEORY FOR HETEROGENEOUS FLUIDS MECHANICS AND HEAT TRANSPORT. OTHER DISCIPLINES
The hierarchical HSP-VAT governing equations for medium or material resulting from the VAT based analysis are mostly the parabolic partial integro-differential equations (PPDE), also they are nonlinear and have additional integral and integro-differential terms. Meanwhile, the great number of optimization problems for Heterogeneous and Scaled media as, for example, for diffusion or electrical transport can be formulated using VAT governing equations. The problems have attractive advantages having the physical as well as morphological (structural) requirements at the same time. This kind of models seems not addressed in research, because the type of HSP-VAT based models were not presented before and there were not need to study the problems. Models that are ordinary surfaced in the control and optimization theory are usually based on the technology requests which have mathematical formulation including problems that can be formulated in area of heterogeneous medium transport. However, the optimization problems involving VAT based formulations of design are more complex then traditional designs and require the new optimization simulation techniques and a complete research to be done for this class of equations, including analysis of necessary conditions and existence of optimal control, as well as developing computational methods for solving various optimal control problems.
There were firstly developed the main definitions and understanding of optimization problems in heterogeneous hierarchical media. Formulated the optimization problem statements for - 1) Heat Exchangers; 2) Semiconductor Chip Heat Sinks. There are a number of traditional techniques applied to the optimization of heat transfer devices such as heat sink enhanced surfaces or heat exchangers. There are, however, no methods or mathematical studies devoted to optimization of hierarchical heat transfer devices. Design optimization procedures for transport in porous structures and enhanced heat transfer surfaces are formulated and developed.
We firstly formulated the definitions of Class and Absolute Optimization in the hierarchical heterogeneous scaled medium. Were developed the methods of solution of distributed optimization problems in heterogeneous media. Has been developed heterogeneous two and three scale volume averaging theory (VAT) volumetric heat dissipation device (VHDD) models and mathematical methods with closure of heterogeneous terms in optimization governing equations. Simulated few canonical and test morphology designs on the lower level of the heat sink heat transport modeling. Volume averaging theory (VAT) was used to optimize heat transport and flow resistance within a specified heterogeneous hierarchical media with multiple scales. VAT Optimization has been advanced to the extent that a statement about
the absolute upper limit can be made and is being used in a practical application. Practical applications include heat generation in solid state devices and semiconductor chips. The work presents itself as a heterogeneous distributed parameters optimization problem.
Among few applications of hierarchical matter and media description the heat generation in solid state devices and semiconductor chips is addressed with the aim to reduce the rate of heat generation and optimize its dissipation.
Developed First Elements of Statistical Theory of Design of Experiments Optimization (DOE) Method for Hierarchical Transport Problems. Ran the simulation experiments and obtained preliminary results. Obtained the results which allow to support the statement about achievable the absolute upper limit of heat dissipation effectiveness on upper scale of VHDD in outlined morphological classes as, for example:
a) 2D longitudinal or transverse regular rib fins; or
b) 3D transversely (cross flow) streamlined regularly located circular cross section arbitrary in 2D( x,z) pin fins; or
c) 3D arbitrary shape regularly located pin fins; or
d) 3D random location circular cross section arbitrary in 2D pin fins; etc.
Mathematical formulation of a hypothetical heat transfer surface with a priori unknown heat transfer enhancing elements has been developed using a two scale description based on volume averaging theory. Second order turbulent model equation sets based on VAT are used to determine turbulent transport and two temperature diffusion in a non-isotropic porous media and inter-phase exchange at a rough wall. Though several different closure models for the source terms for spatial uniform, non-uniform, non-isotropic highly porous layers have been successfully developed, quite different situations arise when attempting to describe processes occurring in irregular, random or even unknown morphologies. After simplification by assuming regularity of the spatial morphology, this problem is still has a large number of optimization space dimensions. In a laminar heat transfer region, the problem is 6 to 8-D and in turbulent it is 8 to 9-D.
As an illustration was elaborated the method of hierarchical optimization of two- and three scale heat transport in a heterogeneous media of a semiconductor heat sink. It is shown how traditional governing equations developed using rigorous VAT methods can be used to optimize surface transport processes in support of heat transport technology. The difficulty in treating a multiparameter (more than 3 ) problem, even linear, known to be very difficult to overcome using a parameter sorting process. The combination of VAT based equations and the theory of statistical design was used to effectively begin treating 6D or 8D optimization volumes.
ACOUSTICS IN HETEROGENEOUS MEDIA
Firstly have been developed multiscale, hierarchical concepts, the approach describing the propagation of the acoustical waves in heterogeneous, scaled, and porous medium using correct scaled mathematical techniques and methods of HSP-VAT. Developed Two scale governing equations are different than widely used models based on Biot equations, other approaches/methods/theories imitating local-nonlocal scaled treatment of wave propagation. New equations of acoustics in heterogeneous and porous medium formulated for some canonical morphologies, as of Biot - straight pores in solid phase.
Developed the theoretical concept, mathematical governing equations and closure approaches (analogous to what had been done for the Volumetrical Heat Dissipating Device) for the Lined Silencer for aerospace industry - done as prospectus for the proposal with consulting company.
Developed the concepts and scaled governing equations for Acousto-Elasticity in porous media. Developed concepts and models for Acousto-Optical coupled phenomena in solid state based on scaled hierarchical description of phenomena.
Among problems in the HSP-VAT heterogeneous Acoustics those already have been solved as the hierarchical two-scale problems should be mentioned here the following:
1) the pretty much known classical problem for capillary medium first tackled as the one (lower) scale task by Biot see, for example in - Biot, M.A., "Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I Low Frequency Range", J. Acous. Soc. Am., Vol. 28, No. 2, pp. 168-178 (1956).
2) the most known and taught in each textbook another classical problem on Acoustical Wave propagation through the multilayer two-phase medium. See the one scale linear solution in - Brekhovskikh, L.M., "Waves in Layered Media," Nauka, Moscow, (1973).
Brekhovskikh, L.M. and Godin, O.A., Acoustics of Layered Media I. Plane and Quasi-Plane Waves, Wave Phenomena, Vol. 5, Springer-Verlag, Berlin, .
ELECTRODYNAMICS IN HETEROGENEOUS MEDIA
Firstly were developed theoretical concepts and theory of electrodynamics in heterogeneous scaled medium using the VAT WSAM theorems. This step allowed to obtain fundamentally different governing equations for electrodynamics in heterogeneous medium based on Maxwell equations and found that the result is not a Lorentz' set of material's electrodynamics equations (Travkin et al., 1999a,b; Travkin and Catton, 2001a; Travkin et al. 2001c;2002).
Developed the physical and mathematical models for multiscale heterogeneous electrodynamics. The physics of polarization and interface transport introduced into the upper scale electrodynamics-heat transfer governing equations. This movement presents the chance to simulate exact polarization processes in and around of matrix submerged objects altogether with the local-nonlocal electrodynamic fields.
Formulated the band-gap problem in photonic crystals as fundamental scaled problem of heterogeneous nature. Developed the VAT description of the non-local band-gap mathematical governing equations for the real heterogeneous media.
Effective scaled heat and charge conductivity were studied for a morphologically simple 1D layered heterostructure with the number of components. The problem is a two-scale media problem with the lower scale physics of energy and charge carriers being described by commonly used models. A continuum - continuum description of nano-microscale transport of electron - phonon energy fields, as well as the electromagnetic and temperature fields for the microscale coupled mathematical models are studied.
The fundamental peculiarities of interface transport and hierarchical mathematical coupling bring together issues that have never actually been addressed correctly. It is shown that accounting for scale interactions and, as is inevitable in scaled problems, application of fundamental VAT theorems to a scaled description of the Laplace and nabla operators bring to the upper scales completely different mathematical governing equations and models. Conducted some quantitative assessment of the differences between the static upper scale and transient nanoscale transport coefficients and show how the superlattice morphology and its irregularities influence the effective conductivities.
Among problems in HSP-VAT heterogeneous Electrodynamics those already have been solved as the hierarchical two-scale problems should be mentioned here the following:
1) The most known and taught, published in each textbook the classical problem on Electromagnetic Wave propagation through the multilayer two-phase (and multiphase) medium. See the one scale linear solution among many other books, for example, in - Brekhovskikh, L.M., "Waves in Layered Media," Nauka, Moscow, (1973) and published later books by this author.
The solution for the Upper scale statement of this problem with the linear Lower scale statement was obtained in few forms, one of them is the completely analytical form.
This is one of the few in HSP-VAT and the first in wave mechanics (some features given also for Ht Acoustics linear problem, which has the pretty much close formulation and solution, in this website) analytical solution for the two scale problem.
Some details are given in -
2) the globular media electrostatics problem when the potential field distributions are sought in regular and in inhomogeneous spatially heterogeneous two-phase media with spherical particle fillers, see in:
Few problems with this kind of morphology have been solved analytically, first of all in thermophysics and fluid mechanics.
3) another textbook's classical problem, which is about an electrostatic potential distribution in the two- (or more) phase superlattice.
Interesting enough, but this problem has been solved for constant coefficients also in a pure analytical (as well as in numerical for inhomogeneous and non-linear media) form
on both scales.
See the two-scale HSP-VAT solution and disappointing comparison with the one scale homogeneous statement solution in this subsection -
ATOMIC SCALE TRANSPORT
Among few applications of hierarchical matter and media description the heat generation in solid state devices and semiconductor chips is addressed with the aim to reduce the rate of heat generation and optimize its dissipation. Developed an approach to the description of the atomic scale - subcrystalline, nanoscale ( actually quantum in nature) electrodynamics through the multiphase spacial (VAT essentially) techniques using mathematical equations for the phenomena and then describing the phenomena for the collective (spatial and timely) behavior. Starting from a set of governing equations for a solid state electron plasma fluid the developed governing field equations are based on heterogeneous medium conservation equations using heterogeneous volume-surface theorems.
In these VAT governing equations the scattering and collision reflecting terms described usually by relaxation time terms are substituted by number of terms each of them reflecting interface specific phenomena including scattering and collision. At the subcrystalline scale energy transport considered the VAT description of crystal defects and impurities on phonon-phonon scattering, which is of substantial importance to understanding the thermal conductivity. At the crystal level, the second level of the hierarchy, the importance of thermal resistance (different models) due to various mechanisms - lattice unharmonic resistance and crystal boundaries defects, addressed. It was shown based on the VAT energy and electrical transport equations that these phenomena should have a great deal of influence on the transport characteristics in applications.
HIGH Tc SUPERCONDUCTIVITY
Developed formulation of the heat transport in a single HTSC crystal- based on the VAT description of subcrystalline (atomic scale) heat transport. Formulation of governing equations and model of HTSC composite as on the second scale - single filament (for example) in the HTSC tape level facilitated along with the coupled nonlinear electrodynamics scaled governing VAT equations in HTSC ceramics. The experimental method and the VAT equations for heat conductivity coefficients in HTSC as the heterogeneous medium have been formulated.
CONTINUUM MECHANICS, ELASTICITY, PLASTICITY, VISCOELASTICITY THEORIES
The unfortunate fact in the contemporary common knowledge continuum mechanics - The Homogeneous Continuum Mechanics (HCM), is that the treatment of the Heterogeneous Media, Matters being performed as those are being indistinguishable from the Homogeneous media treatment!
This failure of Homogeneous Mechanics through the last near 40 years to recognize the other then the accepted in HCM since ~50ths-60ths the mathematical modes (not the theories we can name) by Beran, Hashin, Hill, among others
and continued later in 70ths -- 2000ths by Mura, Nemat-Nasser and Hori, we name just few authors, with the substantial influence as seems throughout the publications of others.
The disastrous influence we can say as long as these and like works, studies have persistently stuck to the idea of using the only tool - the Homogeneous Gauss-Ostrogradsky Theorem (HGOT or GOT) even for the Heterogeneous media. While this is wrong and I think they know that this is wrong, but personal issues prevail mostly over everything in science.
The countless studies appeared in this mode and continue to fill out the literature on Continuum Mechanics published in scientific journals and in books.
We have opening in this website the section on basics of Heterogeneous (Ht) Continuum Mechanics (HtCM). This is good and only starting point in the long run for established HtCM which is also the Theoretical ground (should be at least) for many Heterogeneous and Hierarchical media physical sub-disciplines.
Until the theory of HtCM will be developed to some solid extention, in this section we can state that already the some foundations into the formulation of Elasticity theory, Plasticity, ViscoElasticity -- as the Heterogeneous Two-Scale VAT Governing Equations and models have been developed through the last 10-14 years. That is has been done along with the concepts of Heterogeneous media problems treatment specifically within these fields.
Provided that, we would be glad to publish in this site some analysis of commonly known tasks and their handling while applying the Homogeneous and Ht Elasticity, Ht Plasticity, Ht ViscoElasticity theories. We are talking about the various faces of Homogenization theory considered in HCM as the only possible way of solving the heterogeneous problems.
Among interesting problems we contemplate on the Elastic Solids (Heterogeneous) with Microcavities and Microcracks; Elastic Solids with the Inclusions -- with the second Phase; Elastic Solids with Periodic Microstructures, including the 1D Superlattices; etc.
As everyone knows that the conceptual approaches developed in Continuum Mechanics (we repeat here - within the Homogeneous CM) prevailing for many, many years over the approaches used or "allowed" to use in all the neighboring disciplines. Now we can say that the continued use of the Homogeneous CM for almost any important task formulated on Elasticity, Plasticity, or/and ViscoElasticity in industries is costing a lot not only in terms of financial loss, but with the loss of possibilities of obtaining a correct treatment or solution, or design of the device.
MATERIALS SCIENCE
The natural topics of interest for advancement of scaled phenomena description are those that naturally involve the smallest scales as, for example, from the nanoscale level. As such the nature of ferromagnetism calls for a method, mechanism which is capable to address the scaled subvolumes phenomena of micromagnetism and derive on that basis overall properties, characteristics for the ferromagnetic material. The advantages of hierarchical approach of volume averaging theory (VAT) in description of scaled phenomena with presence of grain morphology of medium or any kind of dividing interface are used for development of mathematical description of ferromagnetic heterogeneous materials electrodynamics.
Starting from magnetic domain process characterization as in the lower scale medium the description of upper scales as crystalline and polycrystalline ferromagnets was developed.
Following this need there have been developed the ferromagnetic heterogeneous materials diffusion, electrostatic and electrodynamics transport VAT three scale governing equations and models.
As it seems now that the better understanding and description of ferromagnetism at the nanoscale level would help in the revision of microscale theories of ferromagnetism. There was developed concept and VAT governing equations for the domain filled crystal, polycrystalline medium and porous ferromagnetic materials. An attempt was made to determine the average dielectric and magnetic properties of powder particles and of a porous medium of a certain BaFe group of ferrites from the material nanoscale characteristics and their models.
The measurements of dielectric and magnetic permittivities of several complex heterogeneous media as : 1) liquid phase, such as water, ethanol, water-ethanol mixtures and water solutions of organic and inorganic substances; 2) dry powders of ferrites; and 3) ferrite powders, saturated with different liquids were made with the aim to connect spatial and phase related structural properties to bulk coefficients.
There were also the technical issues of scaled experiments in porous ferrites which were studied to commence formulation of measurement techniques capable to sustain the basic requirements for scaled experiments.
BIOLOGY AND MEDICINE HETEROGENEOUS, MULTISCALE APPLICATIONS
As it is established in HSP-VAT the mathematical formulation, statements, and modeling of physical processes occurring in strongly heterogeneous media results on the whole in the necessity for the particular medium scaled characteristics development, and accordingly, for process governing equations. This is all applicable to the Heterogeneous Scaled nature of assignments within the Biology/Medicine disciplines.
Among major aims of the HSP-VAT application to Biological/Medicine issues/problems are the following:
1) Provide theoretical derivation of main sets of governing equations (GE) on each level of the hierarchy and estimate feasibility of closure developments.
2) Develop theoretical mechanisms and varieties of closure approaches for each specific biological or/and medicine system hierarchical level.
3) Estimate the feasibility of theoretical procedures for the development of numerical convergent algorithms for solution evaluations of the equations governing the process.
The formulation of Hierarchical Scaled Physics - Volume Averaging Theory (HSP-VAT) principles for polyphase, polyscale biomedia to function and model has been suggested by us firstly in 80s of XX century (Heterogenous biology). The studies since then mostly were made along the self-supported, self-financed path and all novelties appeared because we adhered to the new Heterogeneous polyscale polyphase (HPP) formulations for physical disciplines as acoustics, electrodynamics, nonlinear phenomena, elasticity in heterogeneous solids, wave mechanics, fluid dynamics, thermal physics, etc.
New, unknown to the Homogeneous biology physical phenomena are present and make a role in biological processes. Those can be accounted for in studies and developments of biological, medicine procedures, technologies and experimental methods.
These new techniques for inter-"phase" features proliferation in biomedia are valuable tools (methods) also for an optimization tasks. Processes of protein expression, drug development, drug delivery, and drug impact all have need for optimization of heterogeneous processes.
Some of these HPP physical effects might be guessed; some are new to professionals, as the intermedia surface impact, long-range interaction of proteins (that is known by now only as by qualitative model addition), motor-proteins, enzymes, organelles and continuum fields, cross-communication of different tissue components of two-three physics processes, etc.
All these features can be taken into consideration only via polyscale, poly-"phase" physics interactions.
Among other areas of interests for us in the Ht Biology/Medicine we have been treating the issues related to blood circulation in the variety of human tissues.
Since no single model exists at the present time that could account for multiscaling and consider the actual blood transport within the tissue or organ morphology, we have been working over the suggested earlier by us the development which treats the blood flow in at least four scale heterogeneous systems, including: 1- separate cells (red and white) and dispersed cell medium modeling as well as capillary and arteriole wall scale modeling; 2 - single blood vessel models including previous multiphase scale governing equation statements; 3 - single tissue sample capillary network scale modeling; 4 - finally the three phase blood transport modeling in the tissue morphological vessel networks in conjugation with the soft tissue's phases.
We would like to say that we have been in the stage of conceptual formulation and development of basics of Heterogeneous Scaled (HtS) Bacteriology and Virology as the sciences those utmost functionality are based on the acknowledgment of facts communicated to the existence of the multiscaled collective phenomena of not only the chemical and physical nature.
We would like to make a statement with connection to the nature of these phenomena is that there is the possibility of finding the outstandingly more complicated responses and in vivo behaviour by the facts communicated to the collective scaled nature of cultures and/or tissues existence.
We have been applying the known in HSP-VAT tools while formulating the basic mathematical concepts and models within tasks of/for (HtS) Bacteriology and Virology.
For many biological disciplines we advanced firstly the principles and concepts for HPP modeling of biomedia "in vivo": microbiology, cellular biology, tissue biology, virology, disease modeling, biotechnologies (filtration, biomimetics, etc.).
We developed HPP models for many cellular and tissue processes, bacteriology basic functions modeling for culture, infection progressing, virus invasion stages, etc.
We firstly formulated standard infection problems in bacteriology and virology as HPP mathematical problems - tests in a variety of environments.
Solution and calibration of these problems - tests give a tool for future rapid modeling bac-tests for changed environments or/and strains.
It is of great interest to us the questions related to the functionality and physical and mathematical formulation of the drug development all-together with the disease modeling in vivo. As long as this is profoundly the Heterogeneous Multiscaled Multiphysics and Multiphase task that is the area of only treatable character while with the HSP-VAT approach.
EXPERIMENTAL SCIENCE IN HETEROGENEOUS MEDIA
There was recognition that the experiments and their analysis for homogeneous and heterogeneous media should be modeled differently. The basic studies in the field of heterogeneous scaled energy transport brought the understandings of the theoretical basis for experimental set-ups for heterogeneous hierarchical media. It is well known that the scale of measurements and of the modeling must correspond one to another. This obvious and simple principle is violated when what is clearly a two scale physical problem is described on the upper (measurement) scale with the same kind homogeneous mathematics as is used for the lower scale. Substitution of effective coefficients into models of this type is the primary question that must be dealt with.
Analysis of the known methods of reduction of the experimental results for the heat and momentum transport experiments and development of the VAT based methodology for data reduction in porous media were made. Consistency of the experimental effort and the modeling of the process was emphasized. Common questions of applicability of the experimental data and experimental data reduction was stressed based on the new theoretical basis for modeling of experiments in heterogeneous media. Particularly much of study was done on pressure loss, heat exchange coefficients, and heat conductivity coefficients. Pressure loss and heat transfer experiment analysis procedure developed using VAT as the tool for model formulation and for porous media experimental data reduction.
Developed the fundamentals of Two-Scale Heterogeneous Experimental Technique for Parameters Measurements and Design the volumetric convection heat dissipation devices. This technique was used for semiconductor heat sinks evaluation and comparison purposes. Obtained the exact relationships and improvements to the widely used in industry parameters of heat exchange performance and shown their flaws in terms of assessment and comparison with physical laws.
In an effort to relate the scaled volume average theory (VAT) description and simulation of heat transfer devices (heat sinks) to experimental measurements, there were developed a process of coupling two scale Detailed Micro-Modeling - Direct Numerical Modeling (DMM-DNM) and their corresponding experimental results for few designs of heat sink. It is a problem to properly relate the available local measurements to VAT closure and to measurements within the volume of the heat exchanger (sink). The measurement methods were specified and used for the local and bulk variables data for simulation of the additional terms in the VAT upper scale governing equations.
Described in detail how, and for what reasons, the measured data are to be simulated or measured and represented in a way that allows design goals to be formulated primarily with averaged (or bulk) physical characteristics. Demonstrated why studies of only averaged local integrated variables are not enough. Five sample semiconductor heat sinks of three morphologies were studied by different techniques and models. There were changes in by-pass values, external heat flux and flow rate. Results were depicted using new parameters that better represent the needs of a design process for two-scale devices as well as the usual parameters used in the past. Characteristics reported for the first time are the heat transfer rate in solid phase, relative solid phase effectiveness, and influence of only morphology features among others.
The two scale VAT description equations applicable to the problem have four additional descriptive terms in the momentum equation (for the 1D turbulent equation), seven terms in the fluid temperature equation, and five additional terms in the solid phase (reflecting heat transport through ribs, pins) temperature equations. These additional terms provide far more information about the heat sink and its design than the usual homogeneous models. Most of the additional terms in the VAT equations are terms which based on effects of interface phenomena and field fluctuations acting in the phase. There is, however, a lack of experimental results and data reduction procedures particularly developed for the purpose of experimental closure or verification of VAT heat exchanger governing equations. Contrary to a numerical simulation experiment, the physical experiment is usually much more restrictive in terms of the number and location of local experimental points. There were provided the simulation using the commercial software packages along with the custom developed computational subroutines and user interface. The simulation results were in good comparison with experiments.
Developed Scaled Concepts to Address the Issues of Nanoscale Multiphysics Heat Conductivity Measurement Techniques in electronic materials. The two methods usually applied toward these tasks are made in terms of hierarchical scaled theory of VAT. It has been reported in a number of publications that measured values of superlattice thermal conductivities, for example, GaAs/AlAs, Si/Ge, InAs/AlSb, etc., do not compare well with expected or modeled values. There are questions about measurement techniques that are used and some improvements have been suggested for simulation of the process. One of the used techniques is the 3(omega) measurement of thermal conductivity of superlattices. Another is the Scanning Laser Thermoelectric Microscope (SLTM) technique used for measurement of thermal conductivity and diffusivity of thin films.
The full two-scale heat transport and electrodynamics governing equations were used to achieve understanding of the possible mechanisms that play a role in shaping the effective (measured) coefficients of thermal and electrical conductivities in superlattices. It is shown that the issues of simulation or measurement of the effective coefficients at the upper scale are essentially the same as simulation of the complete two-scale problem in its complexity. Some of these concerns have been dealt with and published in our work, some are in this website -
While also obtained after 2002 the analytical solutions of the following classical problems
that have not been solved for many decades by other methods, we have proven the interscale dependencies of these physical fields
The contribution into understanding of surficial and phase related transport and its inclusion into simulation procedures on the upper scale, and the problem of interaction of charge carriers transport and heat transport on both scales has been made.
AIR POLLUTION MODELING (1976-present)
Urban rough layer - is the layer which main distinguished feature is the actual existence of a two-phase medium in which turbulent transport meteoelements and pollutants occurs. The porous or roughness layer (RL) is the layer between the subsurface and a similar surface running close to the roughness peaks, which is approximately parallel to the subsurface. The structural properties of the roughness layer (obstacle layer) are classified as regular, uniformly rough, non-uniformly rough, randomly rough and highly porous.
Of ever-growing importance are transport processes resulting from of interactions of the atmospheric boundary layer with ground roughness elements. It is natural that problems of atmospheric diffusion and heat pollution in large urban settlements be formulated with an allowance for the interaction of the atmospheric turbulent boundary layer (ABL) with an underlying surface consisting of urban roughness layer (URL) obstacles.
In order to determine and choose a model for turbulent transfer in a URL medium and over it in an ABL, it is necessary to distinguish specific types of models. Depending upon time and space scale descriptions and the quantization of a modeling object, which concern the fields of meteorological elements and pollutants, pollution sources together with the morphologically determined region of their spreading, deterministic or stochastic models may be appropriate. In a city, the main features of an analysis are the nonhomogeneity of the distribution of pollution sources in space and the problem of description or parameterization of the underlying surface roughness.
If the rough surface is described by the function

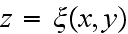 and the root-mean-square deviation of this function,
and the root-mean-square deviation of this function,

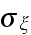 ,
is far greater than the characteristic viscous scale of the boundary layer,
,
is far greater than the characteristic viscous scale of the boundary layer,

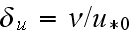 ,
where
,
where

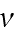 is the coefficient of kinematic viscosity and
is the coefficient of kinematic viscosity and

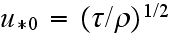 is the dynamic velocity, then the rough or porous subsurface layer properties
are determined by different probability function
is the dynamic velocity, then the rough or porous subsurface layer properties
are determined by different probability function

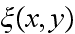 moments, by the viscous scale,
moments, by the viscous scale,

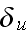 ,
and other morphological characteristics of this layer.
,
and other morphological characteristics of this layer.
An understanding of the ways the two- and three phase URL phenomena of transport have to be modeled with the HSP-VAT scaled approach, which originally was developed for vastly different scale and physical phenomena, was the opening point in development of turbulent transport scaled modeling in porous media and URL. As such the development and application of heterogeneous nonlinear and turbulent phenomena scaled description (HSP-VAT) began with these advancements in air pollution modeling in 1982-86.
Urban Roughness Layer Morphometric Analysis
A technique for obtaining a mathematical description of a surface with a randomly nonhomogeneous roughness layer has been elaborated in 1980-82. The technique is different from the few known methods and is based upon the analysis of morphometric characteristics obtained in the so-called elementary statistical volumes (ESV), into which the urban roughness layer is divided. Afterward the experimental morphometric data can be used in the URL volume averaging theory models.
The method is particularly suitable for roughness layers in which the profilograms are not simple convex or concave curves, but differ in disruptions of curvatures and derivatives, and which are characterized by repeated crossings of normals to the subsurface and by the fact that the vertical dimensions of the nonhomogeneities (obstacles) may be of the same order or greater than the horizontal ones. Morphometrical data in one of new built-up area in city of Kiev were analyzed with the aid of a specialized set of programs for morphometric processing and simulation of experimental data of the URL. Among the morphometric characteristics of the distribution densities to be calculated and evaluated were the distribution densities of surface and volume porosities, of distances between the obstacles and their granular composition, of heights and specific surface of obstacles.
The urban roughness layer turbulent transport VAT models offered not general, but strictly experimental allowance for the morphological characteristics of the randomly nonhomogeneous roughness layer of specific urban housing systems and phytocenosis and made it possible to assess their effect on the characteristics of the turbulent boundary layer and diffusion of harmful impurities in the urban roughness layer. Proceeding from the simulations results for the real urban morphology characteristics in one of local area in the city of Kiev arrived at the conclusion that, specifically, the arrays of experimental data on the harmful impurity concentrations obtained in the lower part of the URL are significantly affected by the morphometric characteristics of the URL properties. It was apparent that available models did not predict the increased levels of concentration of pollutants in the URL nor the atmospheric weather elements.
Later in 1986-1989 these results were used in assessment of ABL pollution problem for the very large oil deposit exploration project "Tengiz" in Kazakhstan, which is due to the presence of high sulfuric gases in oil deposits is not put into regular exploration until now and is the subject for international interest and
investments (including USA - Chevron).
SOIL AND GROUNDWATER CONTAMINATION SCIENCE (SGCS) (1984-present)
Over previous decades, numerous methods have been developed to predict transport and the fate of contaminants in the soil. However, these methods are mostly limited to homogenized one-, two- or, rarely, three-dimensional models and tend to require a high level professionals in order to prepare input data and analyze the results. Typical estimates for exposure and environmental transport currently use multimedia transport models that utilize compartmental models. These models account for the presence of and substance transport through various media in gaseous, liquid or solid phases but tend to obscure the physics of the transport processes both within individual phases and at interface boundaries. Hence, the results of compartmental models combined with uncertainties about the transport properties of specific substances provide, at the very best, an order of magnitude estimate.
A hierarchical physics VAT modeling approach to the solution of soil and groundwater contamination transport alleviates the added degrees of uncertainty by including, instead of marginalizing, the physics of the transport processes.
Theoretical developments in the area of porous-media-transport-processes-modeling, and in groundwater modeling allow one to develop more precise methods of tracing the fate of chemicals released into the soil. It is clear that the coefficient of permeability, K in Darcy law notation can not be used by itself as the influence of many physical mechanisms occurring in porous media fluid flow, even for one-structured morphology, is not contained in its variant models. Homogeneous equations for heat and mass transport in use at this time are only appropriate for small scale laboratory experiments with a simple single structure morphology porous medium (plus conventional approximation of an effective constant coefficients). Effective transport coefficient modeling would be satisfactory if provided on the basis of a specific soil type, the corresponding heterogeneous transport equations and closure modeling developments.
In the soil and groundwater hierarchical method developed, important features and characteristics that are typically omitted from the modeling can be included. Among the many possible extensions and improvements of existing models were consideration of specific soil types and specific morphology, lower level scale fluctuations of variables, cross-effects of different variable fluctuations, phase and interface variable fluctuations effects.
The new integro-differential HSP-VAT transport equations for a heterogeneous soil and groundwater media and applications of these non-classical types of equations is the topical issue. In many cases, quasi-homogeneous and quasi-stochastic methods are not sufficient for description of the physical process featured in the heterogeneous media.
The results of a study of the feasibility of modeling the transport phenomena in a multiscale soil and contaminated groundwater system were reported to DOD ARPA. The smallest scales for continuum phenomena and their modeling for soil and groundwater contamination systems are the cornerstone areas of interest in groundwater modeling. The primary elements of a physical models and new mathematical models for nonlinear transport in different morphological pore systems were developed
based on the HSP-VAT. Modeling at the smallest scale of continuum phenomena resulted in methods for including the effects of colloidal transport and nanoscale phenomena. New mathematical models for nonlinear transport in different morphological pore systems were developed and are described. Analysis of the impact of nonlinear and non-Newtonian viscosity models on flow in nano- and micron scale random pore distribution was made. Morphological analysis of the soil and mining layers and an uncertainty analysis were carried out and results were analyzed.
Software development commencement resulted in several computer based nonlinear transport codes. New results were obtained for the nonlinear transport equations. These numerical simulations show the importance of nonlinear and non-Newtonian transport at the lowest morphology level; pore surface, single pore, primary pore network, random pore size distribution morphology. A top down software design and its analysis were reported.
The methodology developed dealt with flow and solute modeling in a four scale soil systems. The procedure includes: 1- solid-liquid surface scale modeling; 2 - pore scale; 3 - third (small) scale homogeneous porous medium two phase and two-concentration modeling; and 4 - fourth (large) scale heterogeneous porous layer modeling. The modeling procedures suggested are believed to give more accurate results while considering the transport of constituents in each of the phases at each level of the hierarchy.
The study brought the range of results confirmed that morphometrical scaled soil characteristics should be an ingredient in local site assessment and used in the multiscaled soil and groundwater modeling methodology:
The theory of Hierarchical Scaled Physics and Volume Averaging (HSP-VAT) has been applied directly to develop five scales transport equations in soil and groundwater contamination system (SGCS).
In fine pores, it was found that due to polymorphism of the surface fluid layers the modeling should use the structured near surface film of liquids because it is different from that of the bulk liquid. The modified structure of contaminated water was shown to affect the filtration process and leads to inapplicability of the Darcy law.
A dual-porosity "near" pore model was developed featuring a random and irregular interface surfaces (random surface morphology), permeable solid phase model for transport of momentum, mass and heat with the correct boundary conditions on the pore (crack) surface.
Simulation of capillary networks consisting of nodes (various junctions) and pores to model function fluctuations and to use them in closure equations was accomplished. Two computer programs were produced. One simulates very low momentum transport while the other focuses on the non-linear analysis of a capillary network. This effort resulted in a different approach for flow resistance calculations.
A non-Newtonian fluid model has been introduced for use with the specific capillary morphology. Simulation results show the importance of non-Newtonian viscosity model in the modeling of bulk and local transport characteristics.
Analysis of closed forms of the porous medium transport equations developed in this work was accomplished. These equations usually incorporate two features: nonlinearities of different kinds and nonuniformity of porosity.
Analytical solutions and evaluation of some simplified transport equations yielded the tools for analysis of the influence of nonlinearity and nonuniformity of porosity.
Calculations of the flow rates on fine scale in models must take into account the dependence of viscosity on distance from the pore wall. Water boundary layers at nanoscale remoteness from solid phase are characterized by elevated viscosity and do not display a noticeable critical shear stress. Measurements of water flow velocity in capillaries at a number of radii ( ranging from 5x10-2 :m to 1 :m ) have been used to determine the Newton viscosity of water in proximity of a solid hydrophobic surface. The average velocity for variable viscosity was calculated and compared with the average velocity for the Poiseuille flow. For pores with R = 10-1 :m the effect was about 20 %.
Further, much of the previous research results were based on substitution of porous medium properties and functions using artificial network simulation capabilities without satisfying the initial equations. The concern here is that the physical problem, which is simulated with the help of network modeling, must still be modeled in such a way that its initial physical and mathematical statements are properly treated. The development of models of irregular and random networks of pores in the subsurface REV, with consequent substitution of closed morpho-convective and morpho-diffusive terms into the transport equations, was a part of the research.
The key elements in the design of groundwater network models are correct modeling of pore momentum, mass and heat transport and at the same time incorporating the present level of fluid mechanics knowledge about channel junction hydrodynamic resistance. The network model, the junction resistance calculation models are also included as ingredients in the overall hydrodynamic resistance presentation. The goal of network simulation was to close the morpho-convective and morpho-diffusive terms in averaged upper scale transport equations.
The quantitative results of non-Newtonian fluid modeling in porous media differentiate greatly from those for a Newtonian fluid (water) obtained in the groundwater contamination study. An analysis of statistical data modeled on exact solutions for assigned capillary morphology was provided. It showed the tremendous importance of the lowest size pore distribution phenomena. It was found that a negligible part of the overall momentum transport goes through the smallest pores, yet the heat and mass transport through these pores is a large fraction of the bulk transport due to their significant interface transport and enhanced transport peculiarities in fine pores.
Analysis of closed forms of the porous medium transport equations developed in the work was accomplished analytically. These equations usually incorporate two features: nonlinearities of different kinds and nonuniformity of porosity. The closed form of the steady state momentum equation in a porous channel was solved using a Weirstrass function with two invariants. The equation for fluctuating energy was reduced to Abel's equation and expressed in terms of elementary functions.
For relatively small nonlinearities, expansion of the fluid momentum equation solution into a power series allowed one to calculate the mutual influence of nonuniform porosity and nonlinearity. The first terms in the expansion show the influence of nonuniformity alone. For a regular porous structure of spherical packing, the velocity function is expressed in terms of modified Bessel functions. Analytical solutions and evaluation of some simplified transport equations yielded the tools for analysis of the influence of nonlinearity and nonuniformity of porosity.
The following important cases have been analyzed: the existence of simultaneous strong nonlinearity and slowly varying nonuniformity of porosity. If the change in porosity is characterized by a function f(x) with an assumed slow change on the scale of a typical pore radius a, the rescaling of the coordinate z is possible in a way that a new so-called slow variable Z= Lz was used.
Using the nonlinear solutions obtained in the work, a Ginsburg-Landau equation for slowly varying modulation of the equation solution was obtained. This equation is very well studied and its solutions are expressed in terms of Hermitian polynomials allowing one to get analytical solutions for studying many different morphologies.
Are there any other Methods and Theories available?

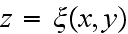 and the root-mean-square deviation of this function,
and the root-mean-square deviation of this function,

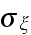 ,
is far greater than the characteristic viscous scale of the boundary layer,
,
is far greater than the characteristic viscous scale of the boundary layer,

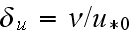 ,
where
,
where

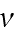 is the coefficient of kinematic viscosity and
is the coefficient of kinematic viscosity and

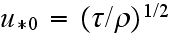 is the dynamic velocity, then the rough or porous subsurface layer properties
are determined by different probability function
is the dynamic velocity, then the rough or porous subsurface layer properties
are determined by different probability function

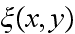 moments, by the viscous scale,
moments, by the viscous scale,

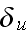 ,
and other morphological characteristics of this layer.
,
and other morphological characteristics of this layer.