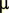 eff=1 for these samples. We will define the effective dielectric function of the inhomogeneous medium in
terms of volume-averaged fields."
eff=1 for these samples. We will define the effective dielectric function of the inhomogeneous medium in
terms of volume-averaged fields."
The Annals of Frontier and Exploratory Science
Vladi S. Travkin
Hierarchical Scaled Physics and Technologies (HSPT), Rheinbach, Germany, Denver, CO, USA
This physical discipline has no genuine features or like one can say the internal deep reasons (principal or just insurmountable) do not abide to the same mathematical theorems as it is known for other like more established fields. Nevertheless, in all but the few places the professionals just confused and respond eagerly with misunderstanding or just demonstrating ignorance with regard of this direction in physics reminding the famous rejection movements (as Luddism) from the past.
The one ground note is that in this section we mostly, but not only after 2010, concern with the classic
homogeneous electrodynamics as it accepts the so-called
Maxwell equations.
Those are not really of Maxwell's original or truncated sets of equations.
Meantime, we take out the original concepts and
governing equations sets as they were done in XIX century and as they
were intended for an aether filled space - homogeneous of course.
That is done with the full attention to the arguments and facts of basic
questionable issues regarding the appearance and formulation of the after
Maxwell-Lorentz (ML) equations.
Again, it is performed in conventional physics textbooks, monographs
as for the
Homogeneous, One Scale for All (OSFA) One Kind Equations for All (OKEFA)
matter and scales physical and
mathematical statements.
The "averaging" procedures accomplished for
Up-scaling of the electromagnetism phenomena in homogeneous physics from the sub-atomic to
mesoscale (macroscale) Continuum mechanics are of the pseudo-averaging
(incorrect) physics and mathematics that
we disclose in a few excerpts and sub-sections in this website.
Several topics we are discussing regarding the basis
for Maxwell-Heaviside-Lorentz (MHL) equations for homogeneous
description of electromagnetism
in a matter. They did not have physical tools and math that were created
later on in XX century.
It must be said here, use the great chance to state
that the conventional homogeneous physics,
which is the electrodynamics mostly, did not use and understand the methods of HSP-VAT widely
is that because of the great culprit and conspiracy (sub-conscious may be) that are hidden behind the
inability of conventional one scale physics to provide the up-scaling, the correct mathematical
averaging in atomic and particle physics since the beginning of XXth century.
They use far and wide the point-particles scheme instead.
While the whole body of orthodox physics stands on
the statement that - the averaging can be and
has been provided within this the one scale physics.
While that is not true, yeah, unfortunately this is a lie.
Nevertheless, they teach students in the way of false one-scale atomic physics
and then based on it the electrodynamics courses
well, for more than 90 years since the Lorentz time. At the beginning and middle of the XXth century
there were no appropriate scaling methods, tools in physics and math. But not after 1967, when they
started to appear. Now it is a lie to say to students - we are teaching at the
state of the art in this and that regarding averaging and what's beyond of it.
2011-2012 - As a result of our work
throughout the last few years we would like to announce the following field's advancements:
That those MHL governing equations - the governing equations that brought to the
present state of affairs in physics, well, not only these we can blame on, the governing
equations that people throughout the last century and at the beginning of this century discovered
many insufficiencies in - remember, that these equations WERE not Developed, they were suggested
as in accordance to the best experimental results of the XIXth century.
Then in a course of XXth century numerous prominent physicists worked hard to justify them and even tried to
"average" from the atomic to a continuum scale description:
These equations that were never correctly lifted -
Scaleported, from the atomic (the common agreement is/was that at atomic scale they work?) to
mesoscale Continuum matter statement,
these equations have been revisited, modified and Scaleported from the Sub-atomic
to the Continuum physics scales.
In several subsections in this section and some other sections
of this website - in
Back to ~2003-2005. We need to
spend here in this discipline some time and effort while returning to basics and argue about few things to address conventional
"wisdom" of old-timers. To do this we would have few comparisons and discuss the few issues down the road. We would like to start
with the few of excerpts from the reviews some physical journals and agencies obtained due to services of EXPERTS in electrodynamics.
One of them was writing:
"....Even more disturbing is the fact that the authors appear to be totally ignorant of the work on physical properties of
macroscopically heterogeneous media that has been going on during the last 20 years. Many of the questions vis-a-vis volume
averaging procedures, which they attempt to raise, were discussed before. They should find out about those earlier discussions and
put their own contribution in a proper context. Two review articles in this field are Isichenko, Rev. Mod. Phys., 64, 961 (1992),
and Bergman and Stroud, Sol. St. Phys., 46, 147 (1992)..."
It was actually a need and a pleasant action (in ~1999) to find some words to comment here
on these sentences. We familiar with these and many other works published on behalf
of "heterogeneous" electrodynamics.
First of all, we can not comment on the all or even many known old and often incorrect
developments in the heterogeneous medium electrodynamics. Simply because it is of low interest,
and because those comments about incorrect definition of word "Averaging" in many physical
disciplines were published for many times in literature on thermal physics, chemical engineering,
and fluid mechanics. This is happened still in the physical literature. There is no secret that
most of established in science people DO NOT READ papers and not interested in studies from
the neighboring physical sciences.
Secondly, we will show now what kind of reasoning applied usually in electrodynamics to the definition of averaging process. Among many others I would take this one.
The paper by Cummings, K.D., Garland, J.C., and Tanner, D.B. (1984), "Electromagnetic Propagation in Random Composite Materials",
in Physics and Chemistry of Porous Media, D.L. Johnson and P.N. Sen, eds., AIP Conf. Proc. 107, pp. 38-51, is the good
example of this kind of reasoning. The paper is well known and often cited.
In the page 40 we can find that:
"Although it may seem that the electric dipole term would specify fully the response of the particle to the applied
plane waves2, it turns out that in the far infrared region magnetic dipole (or eddy current) behavior is often even more
important. This effect, which causes the medium to have a nonzero magnetization even though the constituents are nonmagnetic,
has been discussed by Russel et al. 11, Carr et al. 12, and Stroud and Pan 8. For most of the
samples described in this paper, however, the metal concentration and the frequency of the light are large enough that the magnetic
dipole response has negligible effect on the calculated optical properties. Our model calculations show that we may safely
take 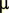 eff=1 for these samples. We will define the effective dielectric function of the inhomogeneous medium in
terms of volume-averaged fields."
eff=1 for these samples. We will define the effective dielectric function of the inhomogeneous medium in
terms of volume-averaged fields."
In their like volumetric averaging they use the definition of averaged fields as (in VAT notation)
 | (1) |
 | (2) |
where the most important thing is that the fields  and
and
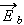 are not visibly averaged, they are taken as the point values, locally. So, the
left hand side of these definitions are non-local, while the right-hand side expressions are local? And this kind of averaging
definition is often taken as sinless?
are not visibly averaged, they are taken as the point values, locally. So, the
left hand side of these definitions are non-local, while the right-hand side expressions are local? And this kind of averaging
definition is often taken as sinless?
The effective dielectric function is defined by
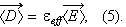 | (5) |
Combining above equations gives the Maxwell-Garnett expression for 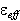 which we label as
which we label as
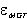
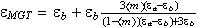
which is possible because acceptance of the formula
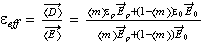
We can not get this formula if to have the non-local right-hand side variables in (1)-(2), because in this case we can not use the formula for one particle solution
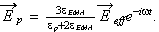
And this is not a unique paper in electrodynamics. This situation is so common for electrodynamics that the whole body of literature on composites is filled with this kind of "analysis".
Consider the typical work - for example, by Levy, O., Bergman, D.J., and Stroud, D.G., "Harmonic Generation, Induced Nonlinearity, and Optical Bistability in Nonlinear Composites", Phys. Rev. E, Vol. 52, No. 3, pp. 3184-3194, (1995).
Here is the paper by the group of well published authors where shown an another example of declared averaging of physical field - where the averaged and local variables are taken as they wanted to be - either local or nonlocal, proclaimed the nonlocal, etc., for example, on p. 3185 we read that - "The volume averaged, or externaly applied, electric field is in this case "
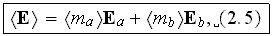
"where

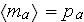 and
and

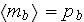 are the volume fractions of the components
are the volume fractions of the components

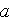 and
and

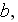 respectively, and
respectively, and

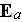 and
and

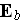 are the local" (outlined by us) "fields in
the two components. The volume averaged displacement field is
are the local" (outlined by us) "fields in
the two components. The volume averaged displacement field is
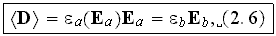
where we used the continuity condition on the normal component of

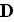 ."
."
Mixing the local relationship for normal components with the non-local
averaged values, as well as using the linear expression

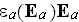 instead of nonlinear dependency for averaged variables is - out of
mathematical critique.
instead of nonlinear dependency for averaged variables is - out of
mathematical critique.
The instant mix of local and non-local variables does not even allow to track the spots where one variable substituted by another one.
Note also that in all these considerations - there is no place for EM governing equations, but the solution for the one particle in the diluted medium!
The solutions of the EM equations are completely separated from the averaging fields ! Well, it's supposed that the averaging is the way simple to obtain. Assuming that after the solution of the one scale conventional Maxwell's equations we just can do fields averaging as is. That's not true anymore after 1967.
Another "expert" wrote in his notes:
"Following that are some unsubstantiated claims that direct numerical modeling...": cannot be a self-sufficient description of heterogeneous media transport:" (It is hard to believe that a numerically exact solution to the exact geometry could have any problems, but that is what is being claimed :.")."
Yes, it is, to the unfortunate conventional one scale physics knowledge. The problem with this vision is - "one point of view, one scale, the basics of many known physics textbooks."
To what disaster this vision had brought in the university education we can see observing the two scale analysis of classical problem in
or watching the ~50+ years old stagnation in Continuum Mechanics
And of course, the disastrous influence of conventional one scale electrodynamics after Maxwell-Heaviside-Lorentz's the best effort, and then as the consequence of the MHL the SR and GR on everything in physics for many decades.
We are talking at different places of this website - that the "averaging" of the obtained via the DMM-DNM variables and "average"-based variables and other derived fields are incorrect when using the homogeneous mathematics and models, due to few reasons. One of them is that the spatial averaging done INCORRECTLY - based on a single volume, and that domain volume is cut and specified to the needs of researchers, not to the true physics and morphology of material or medium. The another reason for inadequacy is - that the Upper scale (averaged) characteristics can not be correctly modeled and simulated using the GO theorem - period, but I am talking about this everywhere. There are few other reasons as well.
Readers can find more explanations in -
FUNDAMENTALS OF SCALING HETEROGENEOUS SCIENCE.
Reading further from the same professional author (it was in ~1998-1999) we can find: "At no point have the authors established that the VAT leads either to a better (either simpler or more accurate) effective medium theory or that it leads to more accurate numerical results."
- The application of HSP-VAT to heterogeneous and scaled media problems leads just not to a "better," but simply to the CORRECT description and results.
We will thoroughly revisit below in this section-science the few "classical" problems with the conventional one scale modeling and applying the two scale HSP-VAT modeling and simulation.
It would be appropriate to give here few notes regarding the priority of the non-local, two-scale, electrodynamics and acoustics HSP-VAT governing equations and concepts developments. As well as on the first heterogeneous problem solutions in Ht Electrodynamics, the two scale solutions.
The first time conceptual solutions and governing equations for the heterogeneous media electrodynamics and acoustics HSP-VAT had been developed in 1997-98 when I was in affiliation with UCLA as a consultant. There was no funding support from government or other sources at UCLA for research in these disciplines (fields). My personal effort in this direction of research was supported at that time (two-three years) by my superior at the MAE department I.Catton solely.
Nevertheless, the theory developments, modeling, simulation, and later on (in 2002-2004) the solutions of the classical problems in Ht electrodynamics have been done without any affiliation to the MAE department, UCLA, whoever was with the UCLA.
There was no professional understanding at the MAE department of UCLA, as and with many other initiatives, by the way.
There were a number of conferences I spoke and presented those HSP-VAT electrodynamics and acoustics concepts, governing equations first in 1998-99:
1) Travkin, V.S., I.Catton, A.T.Ponomarenko, and I.A.Tchmutin, "A Hierarchical Description of Diffusion and Electrostatic Transport in Solid and Porous Composites and the Development of an Optimization Procedure", in ACerS PCR BSD Conf. Proc., p. 20, (1998)
2) Travkin, V.S. and I.Catton, "A Non-Local Hierarchical Model of Thermal Transport in HT Superconductors", in ACerS PCR BSD Conf. Proc., p. 49, (1998)
3) Travkin, V.S., Catton, I., Ponomarenko, A.T., and Gridnev, S.A., (1999), "Multiscale Non local Interactions of Acoustical and Optical Fields in Heterogeneous Materials. Possibilities for Design of New Materials", in Advances in Acousto-Optics'99, SIOF, Florence, pp. 31-32, (1999)
4) Travkin, V.S. and Catton, I., "Local and Nonlocal Thermal Transport in Superstructures - Modeling, Experiments and Combined Electrical - Thermal Conductivities Optimization," in Proc. 5th IUMRS-Int. Conf. Advanced Materials'99, Beijing, Vol. 2, p. 342, (1999)
5) Travkin, V.S., Catton, I., and Ponomarenko, A.T., "Three Scale Hierarchical Modeling of Electrostatics and Electrodynamics in Porous Ferrites; Effective Dielectric Properties and Experiments," in Proc. 5th IUMRS-Int. Conf. Advanced Materials'99, Beijing, Vol. 2, p. 684, (1999)
6) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin, Yu.E., "Few Examples of Improving our Understanding of Relaxation as Transient Physical Process", in Proc. Xxth Conf. RELAXATION PHENOMENA IN SOLIDS, Voronezh, pp. 31-32, (1999)
Then, the first publications with the HSP-VAT governing equations in these fields appeared in 1999:
7) Travkin, V.S., and I. Catton, "Radiation Heat Transport in Porous Media," in Proc. ASME, HTD-364-3, Vol. 3, pp. 31-40, (1999)
8) Travkin, V.S., I. Catton, K. Hu, A.T. Ponomarenko, and V.G. Shevchenko, (1999), "Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis", in Proc. ASME, AMD-233, Vol. 233, pp. 21-31, (1999)
9) Ponomarenko, A.T., Ryvkina, N.G., Kazantseva, N.E., Tchmutin, I.A., Shevchenko, V.G., Catton, I.,and Travkin, V.S., "Modeling of Electrodynamic Properties Control in Liquid-Impregnated Porous Ferrite Media", in Proc. SPIE Smart Structures and Materials 1999, Mathematics and Control in Smart Structures, V.V. Varadan, ed., Vol. 3667, pp. 785-796, (1999)
Following have been the publications and conference talks in 2000+ where I had chances to present more and more results on HSP-VAT electrodynamics and acoustics mathematical formulations and, which is the unique so far situation, the solutions of the two-scale problems in these physical disciplines:
10) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin, Yu.E., Darinskiy, B.M., (2000), "Electrodynamics and Electrostatics in Heterogeneous Media. Effective Properties and their Assessments," in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1028, (2000)
11) Travkin, V.S., Catton, I., Ponomarenko, A.T., Gridnev, S.A., Kalinin, Yu.E., Darinskiy, B.M., (2000), "Ferromagnetism in Scaled Hierarchical Materials. Wave Absorption on Micro- and Macroscale," in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1029, (2000)
12) Travkin, V.S. and Catton, I.., "Transport Phenomena in Heterogeneous Media Based on Volume Averaging Theory", Advances in Heat Transfer, Vol. 34, pp. 1-144, (2001)
13) Ponomarenko, A.T., Shevchenko, V.G., Ryvkina, N.G., Chmureva, V.V., Tchmutin, I.A., and Travkin, V.S., "Electrical Transport and Relaxation Processes in Polymeric Materials: Modeling and Experimental Results", Condensed Matter and Interfaces, Vol. 3, No. 1, pp.73-81 (in Russian), (2001)
14) Travkin, V.S. and Catton, I., "Heat and Charge Conductivities in Superlattices - Two-Scale Measuring and Modeling," in Proc. Intern. Mech. Engin. Congress and Exposition (IMECE'2001), IMECE/HTD-24260, pp.1-12, (2001)
15) Travkin, V.S. and Catton, I., "Analysis of Measuring Techniques for Superlattices Thermal Conductivity Measurements," in Proc. Intern. Mech. Engin. Congress and Exposition (IMECE'2001), IMECE/HTD-24348, pp.1-12, (2001)
16) Travkin, V.S., Catton, I., Ponomarenko, A.T., and Kalinin, Yu.E., "Bottom Up and Top Down, from Nano-Scale to Micro-Scale, Hierarchical Descriptions of Electrodynamic, Thermal and Magnetic Fields in Ferromagnets and HTSCs", in Proc. DOE 20th Symposium on Energy Engineering Sciences, Argonne National Laboratory, pp. 296-304, (2002)
With some level of satisfaction we have to announce here that the publication of the advanced through the years text on fundamentals of new Heterogeneous (Ht) Scaled Electrodynamics, which was prepared in 1998 and at first suggested to "Physical Review Letters" in 1999 (?) had successfully appeared in English in 2004 (!), (the paper was translated into Russian, but the Russian text has not been published) by Springer, see the abstract via this link -
http://www.springerlink.com/app/home/... - "Electrodynamic equations for heterogeneous media..." ,
17) Travkin, V.S. and Ponomarenko, A.T., "Electrodynamic Equations for Heterogeneous Media and Structures on the Length Scales of Their Constituents", Inorganic Materials, Vol. 40, Suppl. 2, pp. S128 - S144, (2004)
The analysis, two scale statements, solutions, as well as the experimental support for the electrostatics (meaning also the thermostatic and diffusion) problems for the three kind of medium morphology can be found in -
18) Travkin, V.S. and Ponomarenko, A.T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 7-17, (2005)
19) Travkin, V.S. and Ponomarenko, A.T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005)
20) Travkin, V.S. and Ponomarenko, A.T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005)
21) Travkin, V.S.
22) Travkin, V.S.
We are continuing to work in this part of physics and at appropriate time new texts will be published.
02/08/2012 - As it was recently brought to my attention - that people stating that there are sprinkled out some publications with the so-called VAT electrodynamics problems - meaning, somehow averaged Maxwell's EM governing equations appeared printed in a textual form. And without mentioning of our first published in 1990s papers referenced here above?
Which is the plagiarism. With this it would be also appropriate to state: that we will be persuing an idea of announcing those workers publishing without reference as the PLAGIATORS in the field, and publicly will continue to advertise this knowledge to their employers.
Back to ~ 2004-2005. The Nonlinear and Inhomogeneous problems are the solely seems my so far specialization, and no other worker correct publication is known to me up to now - . In the Nonlinear and Inhomogeneous Ht Electrodynamics HSP-VAT these advancements until further announcement are in the proprietary sector technology, and can be available based on contractual agreement.
Among problems in HSP-VAT heterogeneous Electrodynamics those already have been solved by us as the hierarchical two-scale problems should be mentioned here the following:
1) The most known and taught, published in each textbook the classical problem on Electromagnetic Wave propagation through the multilayer two-phase (and multiphase) medium. See the one scale linear solution among many other books, for example, in - Brekhovskikh, L.M., "Waves in Layered Media," Nauka, Moscow, (1973) and other published later books by this author. Every book on electrodynamics or acoustics basics has this problem solved as of the One scale.
The solution for the Upper scale statement of this problem with the linear Lower scale statement was obtained by us in a few forms, one of them is the completely analytical form.
This is one of the few in HSP-VAT and the first in wave mechanics (some features given also for Ht Acoustics linear problem, which has the pretty much close formulation and solution, in this website) analytical solution for the two scale problem.
Some details are given in -
2) the globular media electrostatics problem when the potential field distributions are sought in regular and in inhomogeneous spatially heterogeneous two-phase media with spherical particle fillers, see in:
Few problems with this kind of morphology have been solved analytically, first of all in thermophysics and fluid mechanics.
3) another textbook's classical problem, which is about an electrostatic potential distribution in the two- (or more) phase superlattice. Interesting enough, but this problem has been solved for constant coefficients also in a pure analytical (as well as in numerical for inhomogeneous and non-linear media) form on both scales. See the two-scale HSP-VAT solution and disappointing comparison with the one scale homogeneous statement solution in this subsection -
We will continue publishing in this section of the website some developments in HSP-VAT Electrodynamics, the results for educational purposes and for advertisement.
