Travkin HSPT, Thermal Physics

The Annals of Frontier and Exploratory Science

Heat Exchangers. It is the Hierarchical ↑↓ Technology

Among immediate HSP-VAT engineering applications we have been considering the heat exchange devices with volumetric (as well as of surficial) heat exchange features. This vision had been suggested by me in 90s when I was still affiliated with UCLA. Nevertheless, actually the idea was put forward and studied for modeling and design still from the 80s, when I researched the scaled modeling VAT theory applied to the chemical heat- and mass exchangers, chemical reactors.

Need to say here and there, it was completely my development and new in the USA in 90s, while I remember the hardship when was trying to implement this theoretical (at first that was the theory) communication of the two, at least, scale for the HEs modeling and design in the UCLA, MAE's lab in 1994-95s.

Never mind, but it is still used for and at the present time, that the compact heat exchanger (CHE) design is based primarily on utilization of known standard heat exchanger calculation procedures (see, for example, Kays and London, 1984). Typical analysis of heat exchanger designs depends on the simple heat balance equations, which are widely used in the heat design industry. Analytically based models are composed of a properly constructed set of formulae for a given spatial design of heat transfer separate elements that allow most of the existing heat transfer mechanisms to be accounted for.

That means even now after ~ 25-30 years of HSP-VAT promotion regarding the scaled character of heat, mass transfer in devices such as HEs and chemical reactors, at present, simplified theoretical models that are tuned by data that has undergone some statistical averaging process continue representing of heat transport in these apparatuses.

The major drawback of this widely used approach is that it does not give a researcher the ability to directly relate the spatial, morphological, and geometrical features, even when known, to particular phenomena. Often the equations obtained by one researcher using this method are initially different from another without consideration of the further simplifications each might make. This is not the case when the mathematical modeling is based on a rigorous application of the HSP-VAT mathematical approach.

It is an appropriate place in this sub-section for telling some of the story of HSP-VAT application to the HEs theory, modeling, and simulation. The matter is about the authorship and Intellectual Properties (IP) that had been gained outside of some employment (UCLA).

2011. Some Facts from the history of HSP-VAT Founding and HSP-VAT HEs Modeling 1981-2011

As the response to the keynote talk by I.Catton in 2010 - "Conjugate Heat Transfer Within a Heterogeneous Hierarchical Structure" title of his keynote lecture at (IHTC-14) International Heat Transfer Conference, August 8 - 13, 2010, Washington D.C., USA, (http://www.asmeconferences.org/IHTC14/Keynotes.cfm) we need to say some otherwise statements.

In his talk there are wordings - "In 1985, he began his work on Volume Averaging Theory (VAT) as a basis for dealing with transport in heterogeneous hierarchical media. This work culminated in a lengthy paper in Advances in Heat Transfer in 2001. This work has continued and now forms the basis for optimization of heat sinks and heat exchangers."

First of all - Prof. I.Catton could not start the VAT in 1985, as long as I came to the US in 1990, and that was me who named this discipline approximately in 1992-1994 as the VAT (Volume Averaging Theory). Sorry, but I need to disclose this, and this is not in a single case when people liked to get attention via using my IP and publications.

Before that nobody, neither professor S.Whitaker, nor Slattery, nor W.Gray, nor I.Catton ever used the mathematics, physical concepts for heterogeneous (two scale at least) description of physical problems as the scaled ones, two scale at least, for heterogeneous media, for nonlinear fields, for turbulence, biology, medicine, other sciences, etc., etc.

Not talking on the coining of the field as the VAT (HSP-VAT now).

Catton used to deal with the heat exchangers (HE) modeling for many years (and for Nuclear Power industry as well) before me, but never came to the ideas of connecting HE theory, modeling and design to the HSP-VAT, or VAT in the 90s.

Heat Exchangers are the two or more scale thermal and fluid mechanics physics devices.

That was me, who brought all of that on HEs and other fields to the MAE department of UCLA in 1991 and later on performed the theories, mathematical modeling and simulation specifically for HEs in 1998-2002. Using students and collaborators from many countries actually.

See on this in all my - "Fundamentals ......"

especially in "Fundamentals of Hierarchical Scaled Physics (HSP-VAT) Description of Transport and Phenomena in Heterogeneous and Scaled Media"

as well as in this "Heat Exchangers, and in a few other sub-sections.

Regarding the "start" in 1985 - that was the start of porous media research by I.Catton in a completely conventional orthodox way - the one scale homogeneous Darcy-Forchheimer type modeling governing equations, the papers on the topic Catton published with his active grad student J.Georgiadis in those few years before my arrival.

And only my active participation starting in 1991 (Georgiadis left to those days) turned table to the HSP-VAT agenda. I was writing during all the consecutive 11 years to the DOE and DOD, DARPA, corporate research quarters the proposals in the fields of Ht Fluid Mechanics, Ht Thermal Physics, that were the natural fields for the areas of interest at MAE, as well as for other physical sciences that only I had brought in as the Hierarchical, Heterogeneous (Hr, Ht) fields to the department, as the solid state, composites via HSP-VAT, electrodynamics, magnetism, acoustics, medicine, particle physics, nuclear fusion, etc., etc. Have copies of those texts and scripts, if anyone would like to look at.

I.Catton for nearly three years learned the basics to understand and participate in this new for him science. Before my work at MAE of UCLA, he spoke to Whitaker for a few occasions, and left the field unconvinced of its usefulness.

He told me himself on that - "too much of math and what is the goal, the purpose?"

It took, as I said, nearly 3 years before I.Catton had acquired the basics of VAT (HSP-VAT) and began believing in that science (HSP-VAT), and consecutively our program manager of that time at DOE (O.Manly).

And especially, this is my guess, as he witnessed through the years the first of this kind the 2 scale exact solutions in Ht Fluid Mechanics and Thermal Physics which I had developed.

Some even with collaborators from other countries - as Dr. V.Kushch, Dr. Y.Gordienko, Prof. E.Sergievsky, and other personalities, paying to them myself, not via or by UCLA in the 90s.

I.Catton knows about that.

Some of these developments are in the websites, this one - web-1:

http://travkin-hspt.com

and in Russian - web-3: "http://www.travkin-hspt.narod.ru"

And finally for this short history remark, that was me, who wrote the full text of chapter in the book - Travkin, V.S. and Catton, I. Transport phenomena in heterogeneous media based on volume averaging theory// Advances in Heat Transfer, New York, Academic Press, Vol. 34, pp.1-144, (2001). I.Catton was the minor contributor, co-author. He even rejected acceptance of the compensation from the Avademic Press publishing house, because he knew who was the author. We were in good relationship at that time 98-2000, so he gave me his half-part payment. And I'd acknowledged this.

At present times, it would be more modest of I.Catton and fair to write that he "had participated and supported the science of HSP-VAT," but not "started" or "invented," and that he was co-authoring the texts along the major contributor.

Establishment usually attributes all the benefits to themselves in similar situations. Well, with my state of affairs - I am too big fish for that kind of tricks with authorship. Nevertheless, we know the situation in general in the US universities, when the position determines the "major" contributor. This rule is not always truthful, specifically when the lower compensation person having done so many things in the field, that others can not compete.

It is true also, that I.Catton was following my advices in directions from the 90s - 2002, in the HSP-VAT Optimization of HEs, etc. We have many papers written by me. Yes, there are some grad students, other collaborators, but the theory, texts, ideology, mathematics, physical models all were developed by myself with their and I.Catton participations.

Many fields, along with solved problems in HSP-VAT have been done by me and my collaborators in the 80s, before arriving to the US and continue developing HSP-VAT (in physics and math) and its applications far beyond the mechanical engineering at MAE of UCLA as, for example, in meteorology, air pollution science, urban air pollution, chemical engineering, Heterogeneous mathematics, mathematical simulation of Heterogeneous physical problems, atomic, particle and nuclear physics, biology, medicine, for many technologies, etc. Along the area of Heat Exchangers scaled transport as well.

It is interesting - What S.Whitaker, a real one of pioneers since 60s, thinks now on that? In the 90s he told me - that nobody in his department of Chemical Engineering at UC, Davis even understood what he was suggesting and studying. And this is about the really good application field for HSP-VAT such as the chemical reactors modeling and design?

Now, as I wrote here in this website also in the place - "Global Financial Opportunities in Multiscale Technologies. Introduction", other sub-sections,

some people seems, who is somehow familiar with the science of HSP-VAT and publishing close to HSP-VAT, are declaring themselves as the "founders"! And it's a fun to read, but is not true.

Meanwhile, it was the acceptance of the two scales existence in the heat exchange device that was making possible the HSP-VAT approach.

The upper scale space is the space where the whole device or most of it volume is being considered as embedded into the next (upper) scale space with all of it's characteristics and space related properties.

In the below sub-sections the story is told technically and placed with the math and algorithms.

It is an astonishing picture of the heat - and mass exchanger can be seen by everyone visiting the Old Baths of Pompeii, while looking up to the ceiling of the hottest and and the most humid hall (caldarium) in the bath (thermae) complex.

This famous preserved artifacts picture to us is the evidence of highly skilled level of thermal physics understanding by ancient Romans - practical, achieved by hundreds of years of experience in bath construction in the Middle East environment.

It is obvious that the ceiling's picture (drawing) in Wikipedia - "http://en.wikipedia.org/wiki/Thermae", is not following the exact pattern in the morphology of ceiling's structure of Caldarium chamber (the hottest room in these particular baths) selected by ancient builders.

We can observe the presence of the Two-scale grooves all over the ceiling surface

Photo of the Ceiling_of_Caldarium of the Old Baths at Pompeii

Selected piece of the Ceiling_of_Caldarium of the Old Baths at Pompeii

but in the drawing of caldarium pictured in Wikipedia - "Roman Thermae",

Drawing of Caldarium of the Old Baths at Pompeii

and the same selected piece of this ceiling's drawing as we pictured above

drawing of ceiling_of_Caldarium-condenser-Pompeii

The same piece of ceiling in the drawing of Ceiling of Caldarium as in the photo above

shows that the morphology of grooves in the drawing is different.

Did Ancients know better ?

The ceiling as a condenser in the ancient Caldarium, the humid room that had the purpose with this morphology to increase the condensation rate of vapor on the ceiling's surface, to make the vapor condensed and latent heat released (partially) to the hall's volume.

By this Two-scale morphology of the ceiling condenser, the physical conditions in the room had more stimulus' to maintain the temperature in the hottest range, and the convection pattern keeps going from the bottom of the room from those wet and water surfaces to the it's colder ceiling.

Since those antique times already throughout ~XVI centuries after destruction of Roman Empire (Imperium), we could not raise our expectations, our science and experience to get up to the similar level of thermophysics understanding (the two-scale grooves (?), why is that? the presence of grooves in the baths at all?) and the bath culture.

The contemporary designs of Heat Exchangers have the common morphological features.

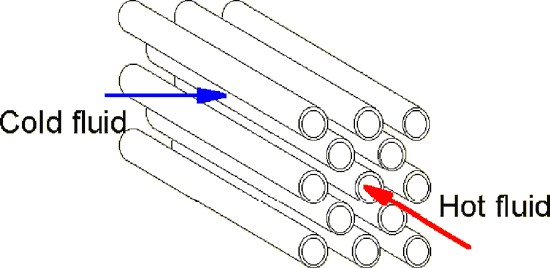
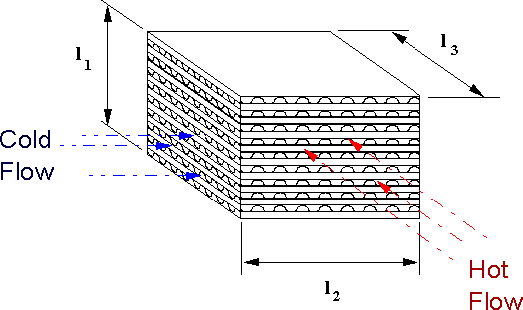
Typical tubular morphology of cross-flow heat exchangers

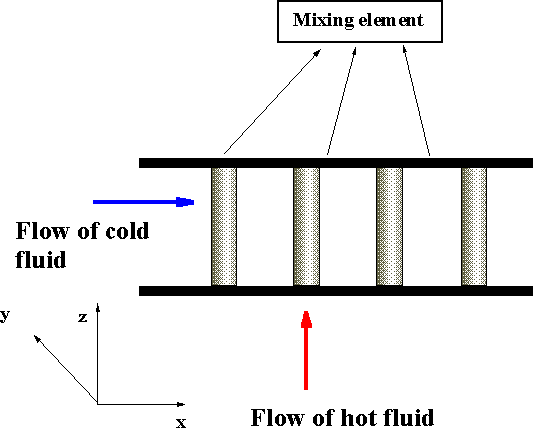
2-D tube heat exchanger unconsolidated morphology to investigate

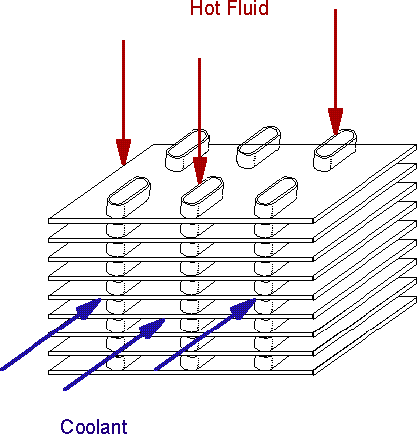
Compact heat exchanger (CHE) with contracted-tubelayer morphology for one of the fluids

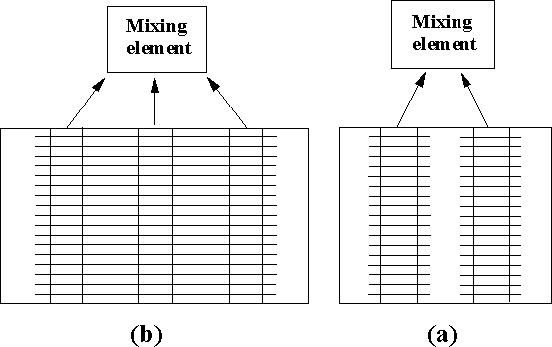
Three-phase unconsolidated - (a), and consolidated - (b), schematic morphology of finned tube heat exchanger

CHE morphology with separated subchannels for each of fluids

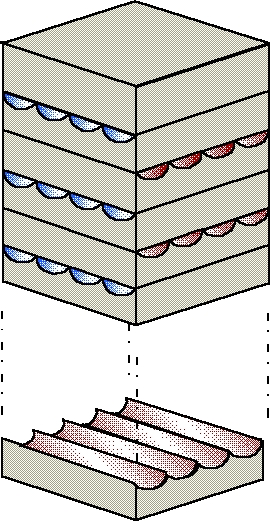
PCHE core zone of heat exchanger

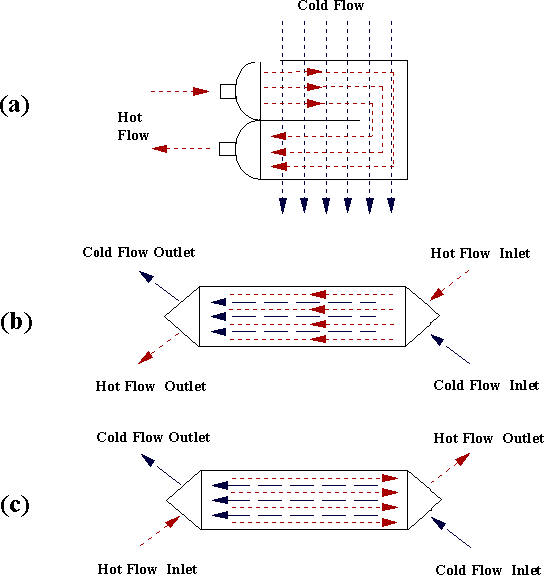
CHE flow arrangements - a) two-pass cross flow, b) co-current flow, and c) counter-current flow

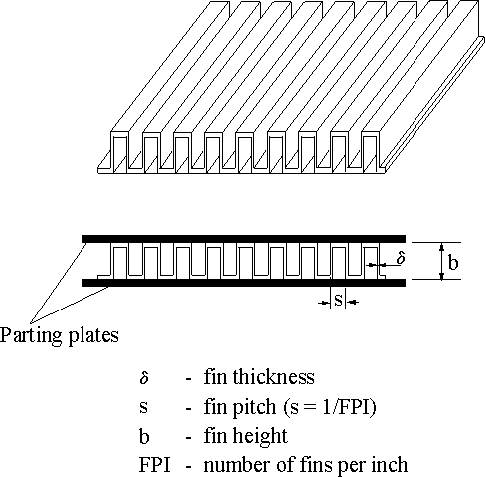
Plain fins geometry

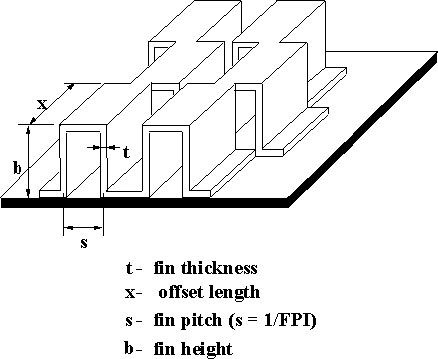
Offset (strip) fin geometry for CHE

Now we would like to turn to the super important issues regarding the Nuclear Reactors components modeling and design that also are of the multi-scale nature by physics and technology itself and by a design of them.

The photos and drawings below are small portion of figures that can be found in the internet and that are openly witnessing in the favor of polyscale and polyphase physics of the processes.

Again, we need to remember that the scale of the product of these devices, reactors function is the Upper scale, bulk in action. Meanwhile, the source of energy production is of so tiny scale that in the theories and mathematical models of these apparatuses the action is given to the one that is the Upper spatial scale (0(10^(-3)-10^(-2))m) mathematical description in a time. The simplified scaled description of these assemblies heat transfer requires at least 3 scales of physics to be accounted for.

Then, if the need is present, and it always exists, the another theory and model for another scale processes have been constructed in the middle of the XX century to justify the physics, mathematics, and "rigorous" approach to the facts, experimental data?

We understand, that those theories were, but not are, of the state of the "art" at that time. Not now, after ~ 1984.

Why of 1984? Because in that year were developed concepts and basics for Non-linear HSP-VAT mathematics and procedures. And nuclear physics and engineering processes are of highly non-linear character.

The start of the compact nuclear reactors design

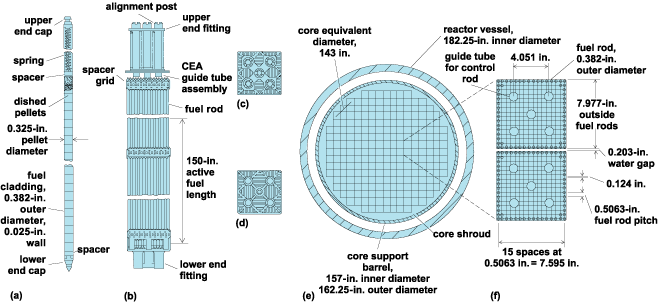
Magnox_reactor_schematic, see in - http://en.wikipedia.org/wiki/Magnox

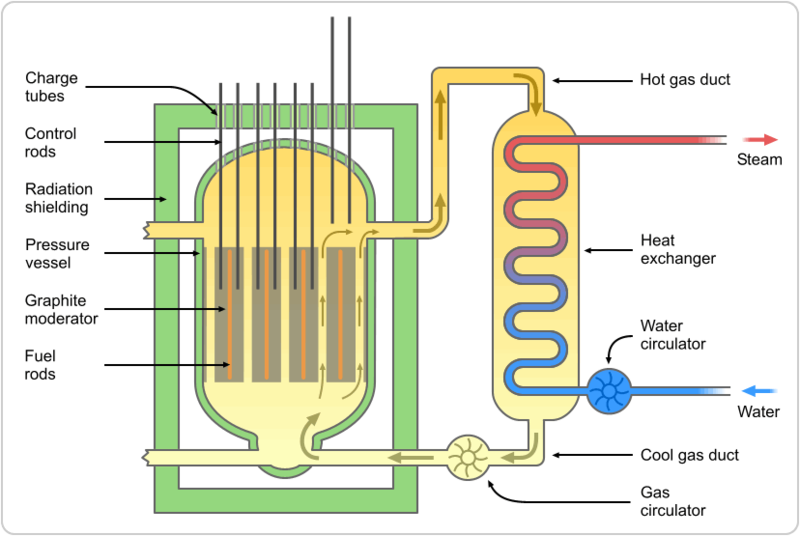
Kadak (2004, 2005)

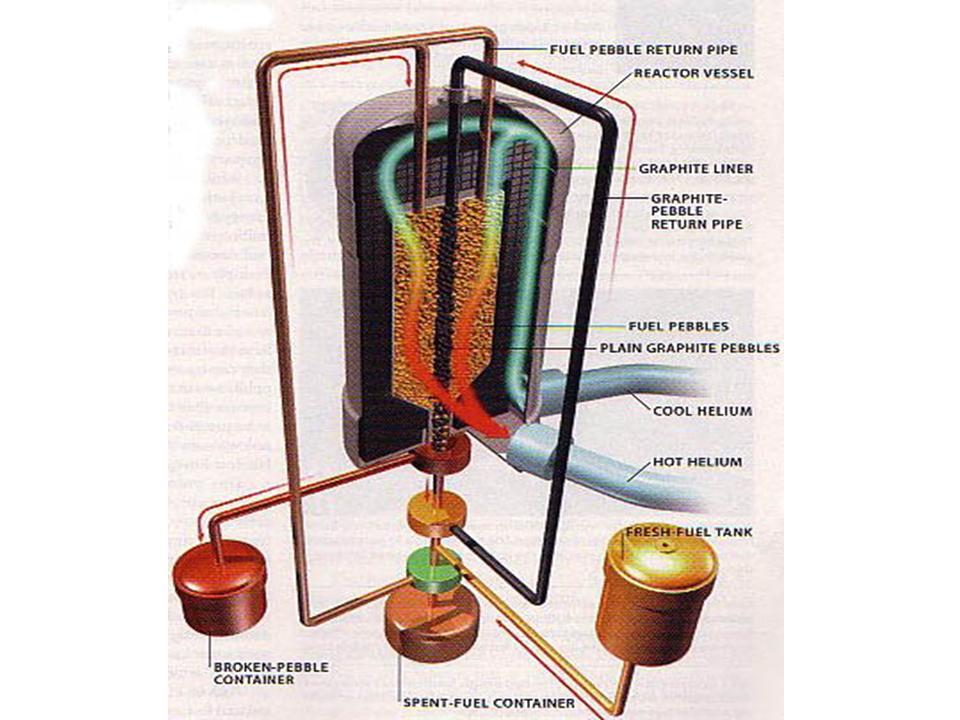
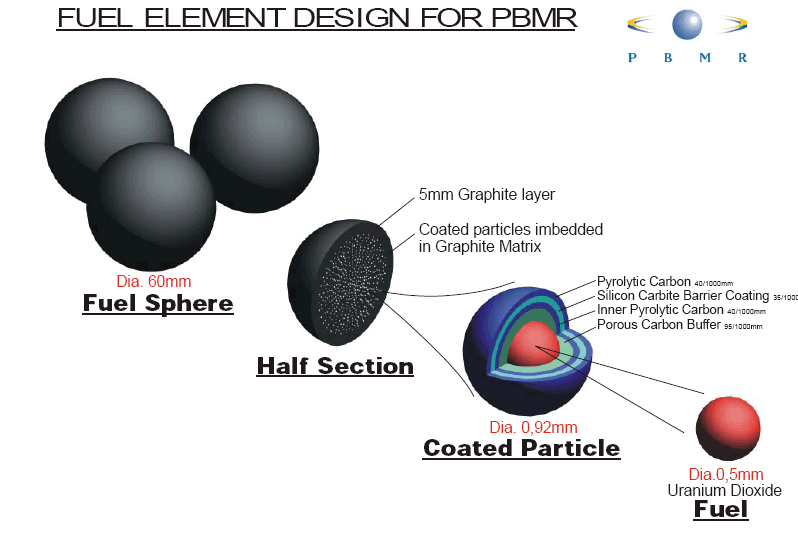
Pebble Bed Nuclear Reactor, Kadak (2005)

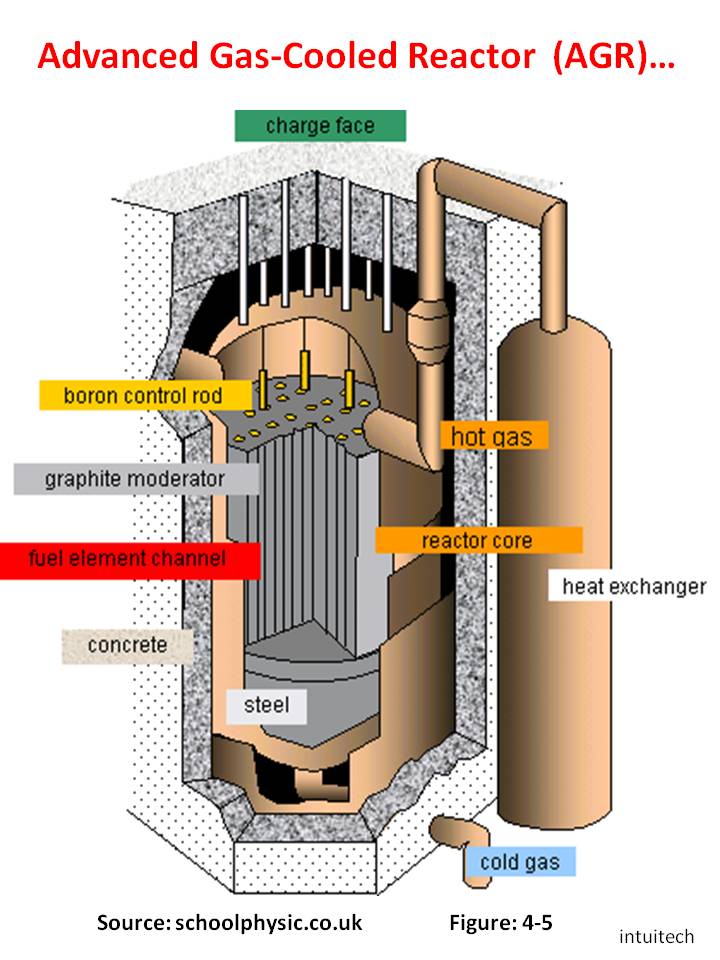
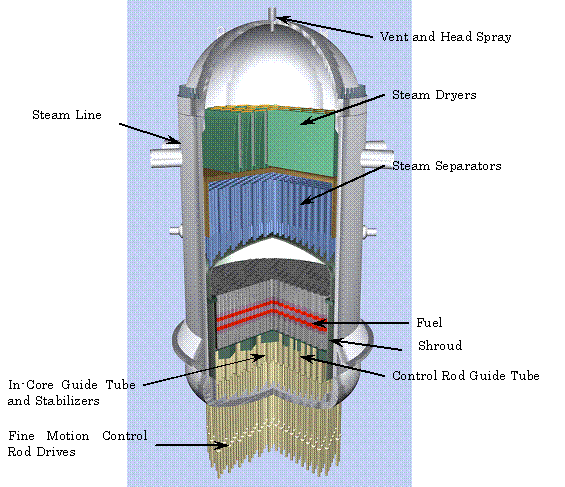
All the Nuclear Reactors' heat generation and exchange physics, structural, model's features are of the HSP-VAT nature - they are polyscale and polyphase. They need to be theorized, modeled and simulated as scaled phenomena in nuclear physics and engineering.

The convincing results of our previous work (and to some extent the studies by workers involved into the two scale research), make possible to apply the HSP-VAT, which is capable to addressing multiscaled as long as the hierarchical heat transport acceleration phenomena that happens to be is the volume with a scaled medium and process.

Some CHE structures have the real appearance and characteristics of a porous medium and can be studied by application of the developments for HSP-VAT porous media modeling. One particular microfoam SiC structure

manufactured by Ultramet http://www.ultramet.com

was used in our previous study to advance the understanding of the scaled approach in application for design the regenerative HE intended for usage in a special automotive application.

A theoretical basis for heat and momentum transport equations obtained with volume averaging theory was developed for modeling and design of heat exchangers. Using different regime transport models, equation sets obtained for momentum transport and two-temperature or three-temperature heat transfer in non-isotropic heterogeneous CHE media that account for interphase exchange and micro-roughness are developed.

This leads to correct mathematical equations for heat exchanger modeling and for optimization by relying on the general field equations rather than on the balance equations. The derived general transport equations for a single-phase fluid in a CHE medium have many more integral and differential terms than the homogenized or classical continuum mechanics equations. Various descriptions of the porous media structural morphology determine the importance of these terms and the range of application of closure schemes. These model equations highlight the various morphological contributors to friction loss and heat transfer lending themselves to optimization of a CHE.

A few outstanding features of the closure models needed to treat the additional integral terms in the equations of flow and heat transfer were described for non-uniformly and randomly structured highly porous media. One-temperature and two-temperature, effective thermal diffusivity models were developed while emphasizing the solid phase micro-scale morphology using different techniques. Additionally, few models were mathematically outlined for various coefficients of drag resistance by implementing a VAT multiple-term superposition approach. Special attention was also given to the evaluation of the heat transfer coefficient dependence upon medium structure in a two-temperature energy models (Gratton et al., 1994, 1995, Travkin and Catton, 1994, 1995, 1998).

Our estimations allowed us to draw the clear line distinguishing the ways to state and approach the hierarchical and consecutive multiscaled heat removal in the high power devices, particularly using a heat sinks for a known or unknown base heat flux. Few main ideas regarding estimation of heterogeneous coefficients and effective coefficients in heterogeneous media as well as the Upper scale HSP-VAT heterogeneous models for heat exchangers were surfaced in few publications, for example, in
Heat Transfer-pgs41-60 (1.0M)
Heat Transfer-pgs61-75 (1.0M)

Some of modeling for design of Compact Heat Exchangers and Semiconductor Heat Sinks (SHS) were done when using the simplified HSP-VAT models with the only one (Upper) scale simulation. These models' closure greatly depends on the availability of experimental data. When the closure models are selected, then the models can be used applying the rather robust numerical simulation schemes developed for the similar kind of HSP-VAT statements as for conjugated heat transport in porous channels -
Numerical Simulation of Conjugate Porous Channels .... (202K)

In some of our works were shown the extension to which the two methodology - Homogeneous One Scale and Heterogeneous Two- and more Scales HSP-VAT, and simplified HSP-VAT can be unified, compared and integrated.

As an example, and one of the most applicable areas we have been considering and studying during many years is a special area of HE - the interesting and urgent topics related to Semiconductor Heat Sinks (SHS) -
Semiconductor Coolers .

Also the fields of Nuclear Physics and Engineering energy generation, heat- and mass exchange devices have found some HSP-VAT development in the section -
"Nuclear Energy, Polyscale Polyphase Structure of Heat Generation and HEx in LWR and HGCR. HtHr Modeling" .

References:

Kadak, A.C., "High Temperature Gas Reactors," MIT Presentation, Briefing to Digital Power Capital, (2005 ?)

Kadak, A.C., "High Temperature Gas Reactors," MIT Presentation, (2004 ?)

Dugan, E.T., "Interim Report on Neutronic Analysis of Hauck Gas Core Reactors for Terrestrial Power Applications," University of Florida, (2009)

http://intuitech.biz/?p=9579 (Chapter 08: Generation IV Advanced Nuclear Reactors)

Heat Exchangers. It is the Hierarchical ↑↓ Technology

2011. Some Facts from the history of HSP-VAT Founding and HSP-VAT HEs Modeling 1981-2011

References:

TO BE ADDED UP