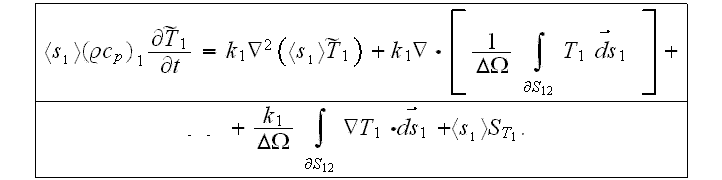
The project "Hydrogen Detectors" has features those involving many phenomena in multilayer materials making the transport of gaseous and fluid substanses through the insulation the two scales, at least, multiphysics problem. Researchers admit among many physical aspects having place in the Electro-Vacuum Thermal Insulation (EVTI) the few physical mechanisms-processes we have been studying because they have the nature of scaled phenomena.
The general structure of EVTI is the multilayer composite material with at least three distinctive scale of physical nature. There are many layers of permeable metal films on the mostly polymeric substrates, separated in turn each from another one by the low heat conductivity porous layers. Roughly it can be considered as the 3 kind of layers (materials) each with different physical and heterogeneous (morphological) characterisitics located in a periodical lattice. The three also major physical fields acting in the composites are the main concerns for modeling and optimization of the structure. These are the heat- and mass, and momentum transport throughout the structure, with addition of electrical or EM fields distribution and the radiation transport happens to be across the EVTI. Pretty much complicated physics, and as such the 3-phase, triple physics, and three-scale system had never been addressed as the VAT based modeling for itself.
The great number of facts evidence in a favor of interface physical processes and are being the important components of a process or transport. There is also evident the need to understand the physics and to model the local, non-local and multiscale characteristics in heterogeneous media.
It is again worthwhile to remind that among the important features of VAT are that it allows specific medium types and morphologies, lower-scale fluctuations of variables, cross-effects of different variable fluctuations, and interface variable fluctuations transport and effects, etc. to be considered. It is not possible to include all of these characteristics in current models using conventional theoretical approaches based on homogeneous Gauss-Ostrogradsky (GO) theorem.
We are working to make some aspects of physics and fields distribution understood better, and modeled as for the three-scale medium. We've been working with the all three major physics fields more or less for many years to have the VAT scaled physics phenomena developed, understood, and applied.
I will repeat below some of the main introductory factual material to lay down the ground as for the three-scale transport approach for the EVTI modeling.
In previous years we have been succeeded in developing the rigorous theory for addressing multi-scale, multi-phase transport phenomena problems in electrodynamics has been proposed on the basis of heterogeneous volume-surface Gauss-Ostrogradsky theorems to treat various aspects of electrical along with thermophysical transport in these media. Heat, mass and electrical transfer models have been developed for media that take into account at least two scales and three phases of the chosen material.
The new scaled Maxwell's field equations have been developed for description of phenomena in heterogeneous media.
The resulting integro-differential equations posses additional ''morpho-'' integral, and ''morpho-'' diffusive terms that are the main issues in the modeling and optimization method development.
Accurate evaluation of various kinds of medium morphology irregularities results from the modeling methodology once a heterogeneous medium morphology is chosen. An attempt was made to classify morphology irregularities associated with different specific kinds of scale morphology and to quantify the impact of irregularities on the mathematical forms of the electrostatic and magnetization governing equations in addition to the impact on the modeling results.
Developed Scaled Concepts to Address the Issues of Nanoscale Multiphysics Heat Conductivity Measurement Techniques in Electronic Materials. The two methods usually applied toward these tasks are made in terms of hierarchical scaled theory of VAT.
It has been reported in a number of publications that measured values of superlattice thermal conductivities, for example, GaAs/AlAs, Si/Ge, InAs/AlSb, etc., do not compare well with expected or modeled values. There are questions about measurement techniques that are used and some improvements have been suggested for simulation of the process. One of the used techniques is the 3(omega) measurement of thermal conductivity of superlattices.
It is well known that the scale of measurements and of the modeling must correspond one to another. This obvious and simple principle is violated when what is clearly a two scale physical problem is described on the upper (measurement) scale with the same kind homogeneous mathematics as is used for the lower scale. Substitution of effective coefficients into models of this type is the primary question that must be dealt with.
Effective coefficient models as thermal and electric conductivities, dielectric permittivity, and reflection coefficent are done at present time on the basis of homogeneous medium governing equations. The models for coefficients constructed on the basis of homogeneous medium provisions do not reflect the most influencial and dominant physical phenomena in the heterogeneous media, as - polarizations, microscale heterogeneities, interface microfields, interplay of different effects, etc. Those described features are the part of the VAT physical and mathematical formulations of problem.
The full two-scale heat transport and electrodynamics governing equations were used to achieve understanding of the possible mechanisms that play a role in shaping the effective (measured) coefficients of thermal and electrical conductivities, and dielectric permittivities in superlattices. It is shown that the issues of simulation or measurement of the effective coefficients at the upper scale are essentially the same as simulation of the complete two-scale problem in its complexity. Some of these concerns have been dealt with elsewhere. We have solved few VAT two-scale problems for superlattice transport contributed to understanding of surficial transport and its inclusion into simulation procedures on the upper scale, and the problem of interaction of charge carriers transport and heat transport on both scales.
Has been developed heterogeneous two and three scale volume averaging theory (VAT) Volumetric Heat Transport Device (VHTD) models and mathematical methods for closure of heterogeneous terms in optimization governing equations. Simulated few canonical and test morphology designs on the lower level of heat transport modeling.
The Method of hierarchical optimization of two- and three scale heat transport in a heterogeneous media of a semiconductor heat sink was formulated and developed for the purpose of hierarchical heat sink design. It is shown how traditional governing equations developed using rigorous VAT methods can be used to optimize surface transport processes in support of heat transport technology. Methods for the optimization of transport characteristics were developed and demonstrated by preliminary results for samples of the fundamental morphologies considered.
They were strictly derived for canonical morphologies. A common occurrence in porous media modeling is the inverse problem requiring the calculation of many coefficients. To obtain the coefficients for a fundamental morphology class, exact closure procedures were derived for layered, capillary, and globular type morphology descriptions at the lowest level scale.
These technical tools, developed and demonstrated, can be used to derive optimization methods for vastly more complex morphologies for VHTDs than those considered before (semiconductor heat sinks).
For the first time, the potential to control transport properties by means of recognizing and manipulating the strict dependencies between the control functions, transport properties and medium morphology (surface system as well) was made available just for heterogneous transport processes.
The same methodology we have been applying to the transport optimization for such devices as the EVTIs. Experience in hierarchical upscale modeling and experimental data reduction techniques for heat transfer and flow in porous and heterogeneous media will be a critical component in the suggested nano- microscale phenomena modeling.
This goal will be achieved using the techniques developed for describing the connection and intercommunication of the phase - interface - phase media properties between the neighboring phases and scales and will include the thermal, electrical phase and effective three-scale coefficients.
We are using one of the generalized forms of two-temperature second upper scale non-local VAT governing equations in heterogeneous medium of EVTI. Based on these forms as will be shown later the whole class of governing equations on micro- and nanoscale levels can be the subject of investigation and treated accordingly.
The solid phase of one of the EVTI layers, for example, averaged equation of heat transfer can be written for the second scale in the form for constant conductivity coefficient
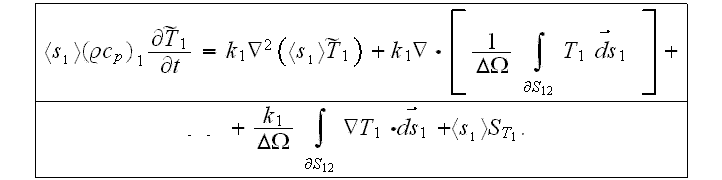
At the same time nonlinear parabolic VAT heat conduction equation in one of the phases of the superlattice EVTI structure is
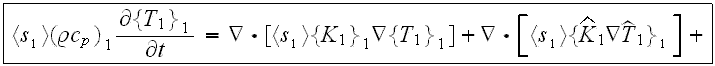
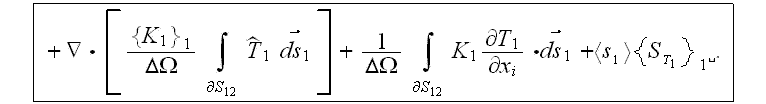
At the same time, as this area is the region of highly diverse methods and techniques the VAT presents itself the indispensable tool for purposes of evaluation and bringing together different methods and quite useful as the most valid basis for comparative validation of techniques using theory and experiment (Travkin et al., 2001a). Equation of second scale heat transport in the second, and third phase would be the same and one can obtains the three-phase temperature model which means actually the hyperbolic types of governing equations (Travkin et al., 2001a).
In our work we will include the interphase boundary thermal resistance into the VAT heat conductivity model in media with three phase morphology. We intend to simulate interface resistance using the integral additional terms in the upper scale VAT governing equations. The influence of these interphase additional terms can be sufficiently high (Catton and Travkin, 1997; Travkin and Catton, 1998).
The main idea in considering the interface zone as the physical object with a finite but very thin thickness helps in understanding why it is different from mathematically assigned surface. This construction allows to manipulate with the transport processes in grain boundaries media as in surficial entities. Meantime, it is the entity which still can be considered as the 3rd medium between known and considered two phases of the composite which can be described as
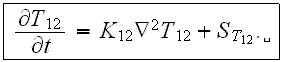
If physical evidencies are good enough to consider the interface in solid
composite medium as the primarily 2D entity (with negligeble thickness ) -
then equation of property transport

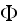 is
is
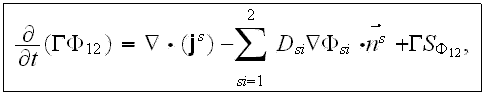
where

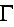 is the surface density or mass per unit area
(
is the surface density or mass per unit area
(
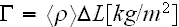 ,
,

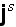 is the property flux within the surface
is the property flux within the surface

 (along this surface). We've developed few surficial models for transport of
mass, energy and EM wave propagation in interfaces (some of the results were
presented at conferences - Travkin et al., 1998a,b; Travkin et al., 1999b,c).
We would like to extend the surficial transport modeling capability in the
current EVTI research applied toward electrodynamics and energy transport
models.
(along this surface). We've developed few surficial models for transport of
mass, energy and EM wave propagation in interfaces (some of the results were
presented at conferences - Travkin et al., 1998a,b; Travkin et al., 1999b,c).
We would like to extend the surficial transport modeling capability in the
current EVTI research applied toward electrodynamics and energy transport
models.
The VAT based 1-D momentum equation for laminar or turbulent flow in void media of each kind of layer's material number 1 is depicted as following
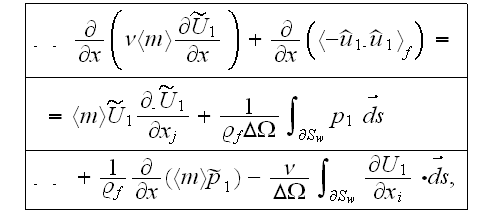
where

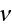 is
the gas kinematic viscosity.
is
the gas kinematic viscosity.
For laminar porous medium flow, the two-temperature energy equation can be
simplified to
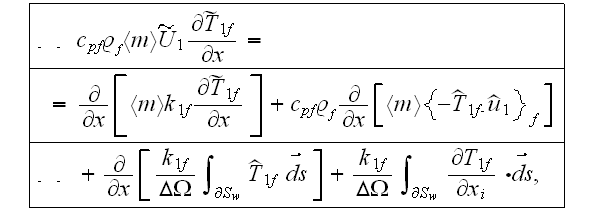 while
in the neighboring solid phase of the same layer, the corresponding equation
is
while
in the neighboring solid phase of the same layer, the corresponding equation
is
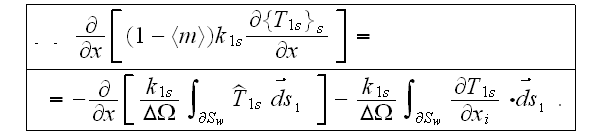
Meanwhile, when coefficient of conductivity (or dielectric permittivity) in the phase one is a constant value then the VAT second scale equation for potential in this phase has the form
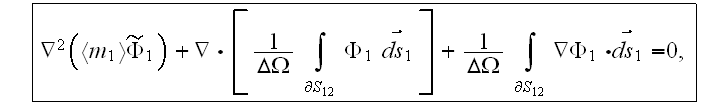
while in the second phase of the same layer
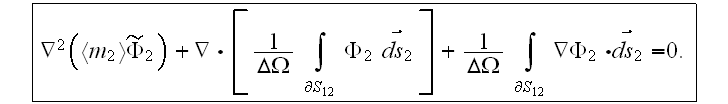
With account for the conservation of current

 at the interface
at the interface

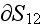
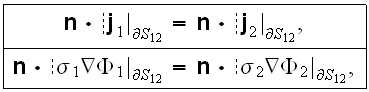
the effective conductivity coefficient determined as
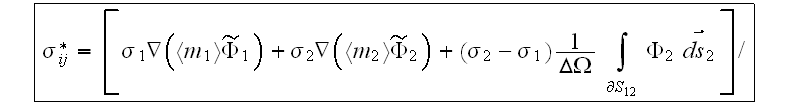
It is worth to note here that the known formula for the effective dielectric permittivity and conductivity of the layered medium is equal

when the electrical field is perpendicular to the interface, is easily (but wrongly) can be derived from the general expression above.
Let's just make an example of the three-phase layered morphology effective
conductivity (permittivity) coefficient (assuming that all three phases are
conductive (dielectric), although it is not really restrictive assumpltion),
then to find out the effective

 for perpendicular electric field, one needs to have at least the lower scale
(second) potential fields solved that allows finally having
for perpendicular electric field, one needs to have at least the lower scale
(second) potential fields solved that allows finally having
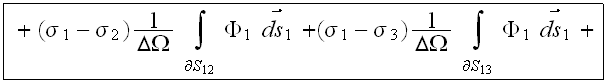
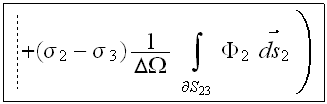
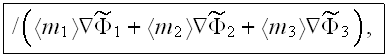 which
seems points out on the quality which first makes impact on the coefficient value, and that is
the relative locations of the layers. Here is the direct connection
between the relative location of the layer and its impact onto the effective coefficient via the temperature distribution within the layer and with its bounding surfaces temperatures.
which
seems points out on the quality which first makes impact on the coefficient value, and that is
the relative locations of the layers. Here is the direct connection
between the relative location of the layer and its impact onto the effective coefficient via the temperature distribution within the layer and with its bounding surfaces temperatures.
The one part of the problem reviewed here with only the two-phase superlattice composite has been evaluated and discussed in this website another subsection -
with the thorough solution given for the electric fields (potentials) (which is valid and for the temperature steady-state distribution) and explanations layed out with the smallest detail in -

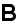 - magnetic flux density
[Wb/m
- magnetic flux density
[Wb/m
 ]
]

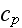 - specific heat
[
- specific heat
[
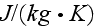 ]
]

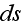 - interface differential area in porous medium
[
- interface differential area in porous medium
[
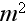 ]
]

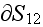 - internal surface in the REV
[
- internal surface in the REV
[
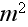 ]
]

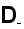 -
electric flux
density [C/m
-
electric flux
density [C/m
 ]
]

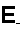 -
electric field [V/m]
-
electric field [V/m]

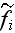



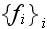 -
VAT intrinsic phase averaged over
-
VAT intrinsic phase averaged over

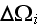 value
value

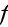

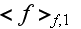 - VAT phase averaged value
- VAT phase averaged value

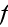 ,
averaged over
,
averaged over

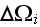 in a REV
in a REV

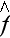 - VAT morpho-fluctuation value of
- VAT morpho-fluctuation value of

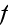 in a
in a

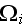

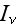 - radiation intensity
[W/(m
- radiation intensity
[W/(m
 sr Hz)]
sr Hz)]

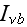 - spectral blackbody intensity
[W/(m
- spectral blackbody intensity
[W/(m
 sr Hz)]
sr Hz)]

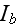 - total blackbody radiation intensity
[W/(m
- total blackbody radiation intensity
[W/(m
 sr)]
sr)]

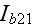 - blackbody specific surface radiation intensity
[W/(m
- blackbody specific surface radiation intensity
[W/(m
 )]
)]

 - current density
[A/m
- current density
[A/m
 ]
]

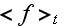 - time averaged value
- time averaged value

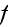

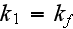 - phase 1 or fluid phase thermal conductivity
[
- phase 1 or fluid phase thermal conductivity
[
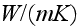 ]
]

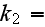 homogeneous thermal conductivity of one of the solid phases
[
homogeneous thermal conductivity of one of the solid phases
[
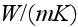 ]
]

 - magnetic field [A/m]
- magnetic field [A/m]

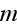 - porosity [-]
- porosity [-]

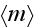 - averaged porosity [-]
- averaged porosity [-]

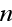 - refraction index [-]
- refraction index [-]

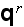 - radiation flux
[
- radiation flux
[
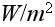 ]
]

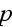 - phase function [-]
- phase function [-]

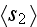 - solid phase 2 volumetric fraction [-]
- solid phase 2 volumetric fraction [-]

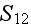 - specific surface of a porous medium in the REV
- specific surface of a porous medium in the REV

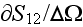 [
[
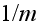 ]
]

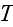 - temperature
- temperature

![$[K]$](/hidro/pic/vacscreen__79.gif)

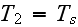 - solid phase temperature
- solid phase temperature

![$[K]$](/hidro/pic/vacscreen__81.gif)

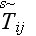 - interface surface temperature when
- interface surface temperature when

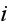 is in upward direction
is in upward direction

![$[K]$](/hidro/pic/vacscreen__84.gif)

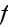

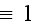 - phase
- phase

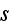

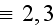 - phase's number
- phase's number

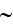 -
value in phase averaged over the
-
value in phase averaged over the

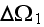

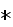 - complex conjugate variable
- complex conjugate variable

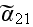 - averaged heat transfer coefficient over
- averaged heat transfer coefficient over


![$[W/(m^{2}K)]$](/hidro/pic/vacscreen__94.gif)

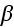 - total extinction coefficient
- total extinction coefficient

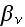 - extinction coefficient [1/m]
- extinction coefficient [1/m]

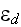

 dielectric permittivity [Fr/m]
dielectric permittivity [Fr/m]

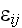 - radiative hemispherical emissivity from phase
- radiative hemispherical emissivity from phase

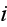 to phase
to phase

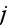 with phase
with phase

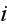 being up into the direction
being up into the direction



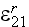 - total radiative hemispherical emissivity from phase
- total radiative hemispherical emissivity from phase

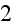 to phase
to phase

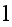 in the REV
in the REV

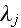 - prescribed Markovian transition length in medium
- prescribed Markovian transition length in medium

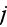 [m]
[m]

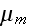 - magnetic permeability [H/m]
- magnetic permeability [H/m]

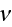 - frequency [Hz]
- frequency [Hz]

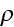 - electric charge density
[C/m
- electric charge density
[C/m
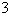 ]
]

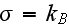 - Stephan-Boltzmann constant
[W/(m
- Stephan-Boltzmann constant
[W/(m
 K
K
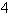 )]
)]

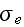 - medium specific electric conductivity [A/V/m]
- medium specific electric conductivity [A/V/m]

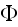 - electric scalar potential [V]
- electric scalar potential [V]

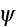 - particle intensity per unit energy (frequency)
- particle intensity per unit energy (frequency)

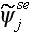 - interface ensemble-averaged value of
- interface ensemble-averaged value of

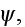 with phase
with phase

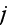 being to the left
being to the left

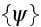 - ensemble-averaged value of
- ensemble-averaged value of

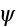

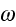 - angular frequency [rad/s]
- angular frequency [rad/s]

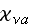 =
=

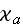 - absorption coefficient [1/m]
- absorption coefficient [1/m]

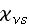 =
=

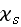 - scattering coefficient [1/m]
- scattering coefficient [1/m]

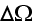 -
representative elementary volume (REV)
-
representative elementary volume (REV)

![$[m^{3}]$](/hidro/pic/vacscreen__130.gif)

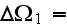

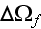 - phase 1 or pore volume in a REV
- phase 1 or pore volume in a REV

![$[m_{3}]$](/hidro/pic/vacscreen__133.gif)

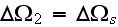 -
solid phase 2 volume in a REV
-
solid phase 2 volume in a REV

![$[m_{3}]$](/hidro/pic/vacscreen__135.gif)
Bakhvalov, N.S. and Panasenko, G.P., Homogenization: Averaging Processes in Periodoc Media. Mathematical Problems in the Mechanics of Composite Materials, Kluwer Acad. Publishers, Dordrecht, 1989.
Barabanenkov, Yu.N., Kravtsov, Yu.A., Ozrin, V.D., and Saichev, A.I., "Enhanced Backscattering in Optics," chap. 2 in Progress in Optics, Vol. XXIX, E.Wolf, ed., Elsevier Science Publ., Amsterdam, pp. 64-197, 1991.
Bergman, D.J., Dielectric constant of a composite materials - problem in classical physics, Phys.Rep., vol. 43, 378-407, 1978.
Bergman, D.J., Dielectric constant of a two-component granular composite: a practical scheme for calculating the pole spectrum, Phys.Rev. B, vol. 19, 2359-2368, 1979.
Busch, K. and Soukoulis, C.M., (1995), " Transport Properties of Random Media: A New Effective Medium Theory," Phys. Rev. Lett., Vol. 75, No. 19, pp. 3442-3445.
Cahill, D.G., Fischer, H.E., Klitsner, T., Swartz, E.T., and Pohl, R.O., (1989), "Thermal Conductivity of Thin Films: Measurement and Understanding," J. Vacuum Scienc and Technology A, Vol. 7, pp. 1259-1269.
Cahill, D.G., (1990), ''Thermal Conductivity Measurement From 30-K to 750-K -
The
3
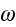 Method,''
Method,''
Rev. Sci. Instrum., Vol. 61, pp. 802-808.
Cahill, D.G., Waston, S.K., and Pohl, R.O., (1992), ''Lower Limit to the Thermal Conductivity of Disordered Crystals,'' Physical Review B, Vol. 46, pp. 6131-6140.
Cheng, H. and Torquato, S. (1997). Electric-field fluctuations in random dielectric composites. Physical Review B 56, 8060-8068.
Fushinobu, K., Majumdar, A., and Hijikata, K. (1995), "Heat Generation and Transport in Submicron Semiconductor Devices", J. Heat Transfer, Vol. 117, pp. 25-31.
Flik, M.I., Choi, B.I., and Goodson, K.E., (1992), ''Heat Transfer Regimes in Microstructures'', J. Heat Transfer, Vol. 114, pp. 666-674.
Jensen P., Barabasi A.-L., Larralde H., Halvin S., Stanley H.E., "Deposition, diffusion and aggregation of atoms on surfases: A model for nanostructure growth," Phys. Rev. B.,1994., V. 50, N20, pp. 15316-15329.
Goodson, K.E., (1996), "Thermal Conduction in Nonhomogeneous CVD Diamond Layers in Electronic Microstructures," J. Heat Tarnsfer, Vol. 118, pp. 279-286.
Gray, W.G. and Hassanizadeh, S.M. (1989). Averaging theorems and averaged equations for transport of interface properties in multiphase systems. Int. J. Multiphase Flow 15, 81-95.
Gubernatis, J.E. (1978), "Scattering Theory and Effective Medium Approximations to Heterogeneous Materials", in Electrical Transport and Optical Properties of Inhomogeneous Media, J.C. Garland and D.B. Tanner, eds., AIP Conf. Proc. No. 40, New York, pp. 84-98.
Gusev, A.L., " Квазиконденсаторный" эффект в криогенно-вакуумных объектах с экранно-вакуумной теплоизоляцией (ЭВТИ)," in Вопросы атомной науки и техники серия (вакуум, чистые материалы, сверхпроводники) вып. [4(5), 5(6)]. - 1998, с.129, (in Russian).
Gusev, A.L., "Низкотемпературная регенерация криоадсорбционных устройств в теплоизоляционной полости водородного криогенного резервуара.// Вопросы Атомной Науки и Техники. Сер. Вакуум, чистые материалы, сверхпроводники. Харьков. ННЦ «Харьковский Физико-технический Институт», 1999, вып. 1(9), стр.19-27, (in Russian).
Landauer, R. (1978), "Electrical Conductivity in Inhomogeneous Media", in Electrical Transport and Optical Properties of Inhomogeneous Media, J.C. Garland and D.B. Tanner, eds., AIP Conf. Proc. No. 40, New York, pp. 2-45.
Levy, O. and Stroud, D., Maxwell Garnett theory for mixtures of anisotropic inclusions: Application to conducting polymers, Phys. Rev. B, Vol. 56, 8035-8046, 1997.
Михальченко Р.С., Першин Н.П., Клипач Л.В., "Экспериментальное исследование пропускной способности слоисто-вакуумных изоляций," in Гидродинамика и теплообмен в криогенных системах, Киев, 1977, с.79-86 (in Russian).
Михальченко Р.С., Гетманец В.Ф., Клипач Л.В., Юрченко П.Н., "Экспериментальное исследование газопроницаемости ЭВТИ на основе перфорированных экранов," ИФЖ, №1, Vol.53, 1987.
Ponomarenko, A.T., Ryvkina, N.G., Kazantseva, N.E., Tchmutin, I.A., Shevchenko, V.G., Catton, I.,and Travkin, V.S., (1999), "Modeling of Electrodynamic Properties Control in Liquid-Impregnated Porous Ferrite Media", in Proc. SPIE Smart Structures and Materials 1999, Mathematics and Control in Smart Structures, V.V. Varadan, ed., Vol. 3667, pp. 785-796.
Ponomarenko, A.T., Shevchenko, V.G., Ryvkina, N.G., Tchmutin, I.A., and
Travkin, V.S., (1999), ''Electrical Transport and Relaxation Processes in
Polymeric Materials: Modeling and Experimental Results'', in
Proc.

 RELAXATION
PHENOMENA IN SOLIDS, October 19 - 22, Voronezh, RUSSIA, pp. 9-10.
RELAXATION
PHENOMENA IN SOLIDS, October 19 - 22, Voronezh, RUSSIA, pp. 9-10.
Rizzi, M., Canino, M., Hu, K., Jones, S., Travkin, V. S., Catton, I., ''Experimental Investigation of Pin Fin Heat Sink Effectiveness'', Proceedings of NHTC'01 35th National Heat Transfer Conference, Anaheim, California, June 10-12, 2001.
Ryvkina, N.G., Ponomarenko, A.T., Tchmutin, I.A., and Travkin, V.S., (1998), ''Electrical and Magnetic Properties of Liquid Dielectric Impregnated Porous Ferrite Media,'' in Proc. XIV-th International Conference on Gyromagnetic Electronics and Electrodynamics, Microwave Ferrites, ICMF'98, Section Spin-Electronics, Vol. 2, pp.236-249.
Ryvkina, N.G., Ponomarenko, A.T., Tchmutin, I.A., Travkin, V.S., and V.G.Shevchenko, (1999), ''Liquid-Impregnated Porous Media: Structure, Physical Phenomena, Electrical Properties'', Materials, Technologies, Tools, Vol. 4, No. 1, pp. 27-41, (in Russian).
Rytov, S.M. (1955), "Electromagnetic properties of a Finely Layered Medium", Zh. Eksp. Teor. Phys. (Sov. Phys. JETP), Vol. 29, pp. 605-615.
Sarychev, A.K. and Vinogradov, A.P. (1983), "Effective Medium Theory for the Magnetoconductivity Tensor of Disordered Materials", Physica Status Solidi, B, Vol. 117, No. 2, pp. K113-K118.
Scurlock, R.G, Saull B., "Development of Multilayer Insulations With Thermal Conductivities Below 0.1," Cryogenics, 16, 303, 1976.
Shalaev, V.M. and Sarychev, A.K., (1998), "Nonlinear Optics of Random Metal-Dielectric Films", Phys. Rev. B, Vol. 57, No. 20, pp. 13265-13288.
Travkin, V.S. and Catton, I., "Porous media transport descriptions - non-local, linear and nonlinear against effective thermal/fluid properties", in Advances in Colloid and Interface Science, Vol. 76-77, pp. 389-443, 1998a.
Travkin, V.S. and Catton, I., ''A Non-Local Hierarchical Model of Thermal Transport in HT Superconductors'', in ACerS PCR & BSD Conf. Proc., p. 49, 1998b.
Travkin, V.S., Catton, I., Ponomarenko, A.T., and Tchmutin, I.A., ''A Hierarchical Description of Diffusion and Electrostatic Transport in Solid and Porous Composites and the Development of an Optimization Procedure'', in ACerS PCR & BSD Conf. Proc., p. 20, 1998c.
Travkin, V.S., Catton, I., Ponomarenko, A.T., and Gridnev, S.A. (1999a), "Multiscale Non-local Interactions of Acoustical and Optical Fields in Heterogeneous Materials. Possibilities for Design of New Materials", in Advances in Acousto-Optics'99, abstracts, SIOF, Florence, pp. 31-32.
Travkin, V.S. and Catton, I. (1999b), "Local and Nonlocal Thermal Transport in Superstructures - Modeling, Experiments and Combined Electrical - Thermal Conductivities Optimization," in Proc. 5th IUMRS-Int. Conf. Advansed Materials'99, abstracts, Beijing, Vol. 2, p. 342.
Travkin, V.S., Catton, I., and Ponomarenko, A.T. (1999c), "Three Scale Hierarchical Modeling of Electrostatics and Electrodynamics in Porous Ferrites; Effective Dielectric Properties and Experiments,"
in Proc. 5th IUMRS-Int. Conf. Advansed Materials'99, abstracts, Beijing, Vol. 2, p. 684.
Travkin V.S., Catton, I., A.T.Ponomarenko, A.T., Gridnev, S.A., Yu.E. Kalinin,
Yu.E., (1999d), "Few Examples of Improving our Understanding of Relaxation as
Transient Physical Process", in Proc.

 RELAXATION
PHENOMENA IN SOLIDS, pp. 31-32.
RELAXATION
PHENOMENA IN SOLIDS, pp. 31-32.
Travkin, V.S., Catton, I., Hu, K., Ponomarenko, A.T., and Shevchenko, V.G., (1999e), ''Transport Phenomena in Heterogeneous Media: Experimental Data Reduction and Analysis'', in Proc. ASME, AMD-233, Vol. 233, pp. 21-31.
Travkin, V.S. and Catton, I., (1999f), ''Nonlinear Effects in Multiple Regime Transport of Momentum in Longitudinal Capillary Porous Medium Morphology'', J. Porous Media, Vol. 2, No.3, pp. 277-294.
Travkin V.S., Catton, I., A.T.Ponomarenko, A.T., Gridnev, S.A., Yu.E. Kalinin, Yu.E., B.M. Darinskiy, B.M., (2000a), ''Electrodynamics and Electrostatics in Heterogeneous Media. Effective Properties and their Assessments,'' in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1028.
Travkin V.S., Catton, I., A.T.Ponomarenko, A.T., Gridnev, S.A., Yu.E. Kalinin, Yu.E., B.M. Darinskiy, B.M., (2000b), ''Ferromagnetism in Scaled Hierarchical Materials. Wave Absorption on Micro- and Macroscale,'' in Proc. PIERS'2000: Progress in Electromagnetics Res. Symp., p. 1029.
V.S.Travkin, V.S. and Catton, I., (2001a), "Transport Phenomena in Heterogeneous Media Based on Volume Averaging Theory", in Advances in Heat Transfer, Vol. 34, pp.1-144.
Travkin, V.S., Hu, K., Rizzi, M., Canino, M., and Catton, I., (2001b), ''Revising the Goals and Means for the Base-to-Air Cooling Stage for Semiconductor Heat Removal - Experiments and Their Results,'' in Proc. 17th IEEE SEMI-THERM Symp., pp. 85-94.
Travkin, V. S., Hu, K., and Catton, I. (2001c), ''Multi-variant Optimization in Heat Sink Design'', Proceedings of NHTC'01 35th National Heat Transfer Conference (2001 NHTC).
Travkin, V.S. and Catton, I., (2001d), "Heat and Charge Conductivities in Superlattices - Two-Scale Measuring and Modeling," IMECE'2001.
Travkin, V.S. and Catton, I. (2001e), "Analysis of Measuring Techniques for Superlattices Heat Conductivity Measurements," IMECE'2001.
Travkin, V. S. (2001), "Relating the Semiconductor Heat Sink Local and Non-Local Experimental and Simulation Data to Upper Scale Design Goals", IMECE'2001.
Rizzi, M., K. Hu, E. Huckle, S. Jones, V.S. Travkin, I. Catton, (2001), "Experimental Investigation of Pin Fin Heat Sink Effectiveness," in 35th ASME National Heat Transfer Conference, 2001
Uher, C., "Thermal conductivity of
high-T
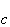 superconductors,". J. Superconductivity, Vol.
3, pp.337-389, 1990.
superconductors,". J. Superconductivity, Vol.
3, pp.337-389, 1990.
Zolotarev, P.P. and Radushkevich, L.V., "The Equations for Dynamic Sorption in an Undeformed Porous Medium, Doklady Physical Chemistry," Vol. 182, pp. 643-646, 1968, (in Russian).
![]()