Two Scale Two-Phase Straight Bars (Capillaries) Electrostatic Exact Solution

This is the next problem from a classical list we liked to explore to find out the possibilities for the observable understandable solution for the problem within the mutual HSP-VAT content. And at the same time this problem also has been passing to a worker the challenge to figure out - What is the difference between the conductivity in a medium with just one conductive bar in a dielectric matrix and a conductivity coefficient when a bunch of bars distributed in the same dielectric? For the diluted bar distribution we have the long ago known mathematical formulation.

The difference also would be due to the mode (way) formulating the solution as for the bulk medium conductivity. We state that this is the same kind of the two scale problem which needs to be formulated for the both scales, not just for the lower one.

Here is the problem, which for some statements can be solved analytically as well. Few features remind the solution of the Upper scale momentum transport in the three regime capillary porous medium with the straight capillaries in the study by

Travkin, V.S. and Catton, I., "Nonlinear Effects in Multiple Regime Transport of Momentum in Longitudinal Capillary Porous Medium Morphology", J. Porous Media, Vol. 2, No.3, pp. 277-294, 1999. We will try to make parallels between mathematical statements for both problems and between the two scale solutions.

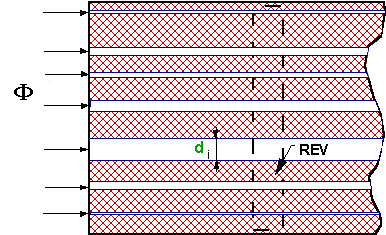
Straight bars or capillaries crossing through the dielectric layer.

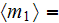
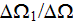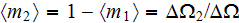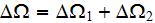Let's consider a two-phase heterogeneous medium consisting of an isotropic dielectric continuous (solid) matrix and an isotropic discontinuous phase (bars or capillaries). The volume fraction of matrix, or 1st phase, is , the volume fraction of filler, or 2nd phase, is , where is the volume of the REV. The constant properties (phase conductivities, 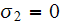and 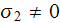) control the stationary (time-independent) electric potential field differential equations for 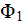and .

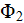If one regards a problem of the electrical potential distribution in a separate single conductive capillary or tube of circular cross-section in a bundle of capillaries, when on the one side of the tube is the absolute conductor with the potential given as 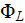and on another side of the tube the potential of the cross-section is 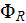and when 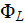> 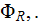with the difference of potentials is 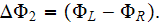Then the electrostatic potential field 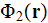( 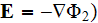inside of the capillary will comply to the Laplace equation

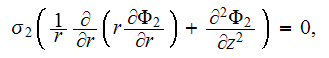
inside of the second phase volume 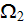with the usual simplified boundary conditions

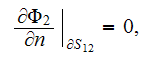	(1)

where 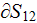is the wall surface of the capillary, and

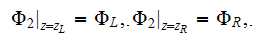	(2)

where 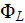and 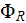are the potentials on both sides of medium slab applied that the unit voltage drop corresponds to the unit length in the primary z-direction described by unit vector

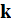
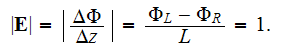
If there are many capillaries in the slab and they are all directed in z-direction, then the potential drop and the pressure drop if the fluid is moving inside of capillaries are all of the same values

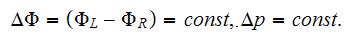
We can treat the model of parallel capillaries or tubes with random diameters. If capillaries are aligned in the direction of unit vector 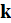which is the unit vector along of z-coordinate, then the upper scale VAT conductivity equation for the conductive medium (second phase) of capillaries

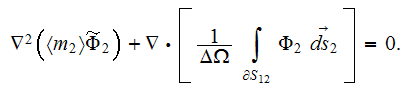	(3)

which is for one dimension (with constant 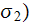upper scale equation yields the form

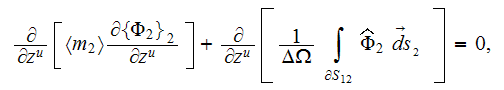
where is the upper scale space coordinate coinciding in direction with the lower scale space z-axis.

Due to 1D spatial character of the upper scale VAT potential function equation it will take the following form in cartesian coordinates of the problem's upper scale space

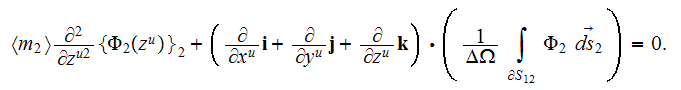
Adopted boundary conditions (1), (2) bring the lower first scale potential equation to

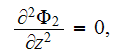
which is the single attractive feature of this simplified first scale (conventional) model. The solution for the potential inside of the 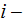th capillary will be

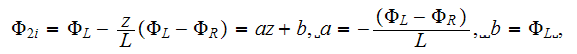
with the current

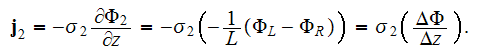
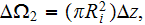
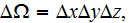
Note, that there is no participation of the second phase potential, because the problem stated as the non-conjugated one. After taking 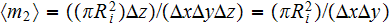for each capillary, one can calculate the average potential variable for variable one diameter capillary morphology (taking the point 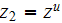of the lower scale coordinate system as the representative point in the upper scale coordinate system, which has no principal difference for the result)

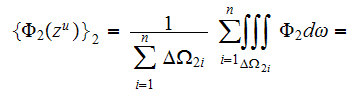
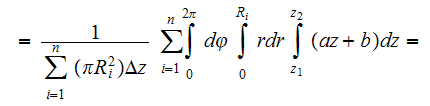
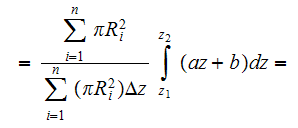
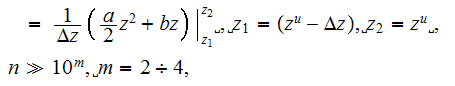
or

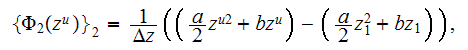
which results in calculation of the first term in equation (3)

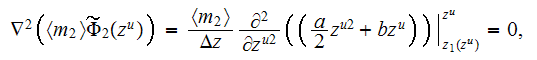
note that

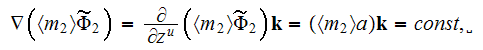
while the second term in equation (3) also comes to zero (for easier demonstration take the cylindrical REV 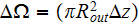for the one separate 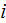-th capillary, that does not have difference for final result)

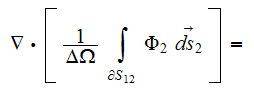
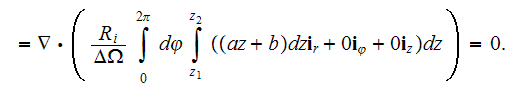
That means the upper scale VAT equation for the capillaries medium is satisfied for the regions inside of the layer's boundaries by the function

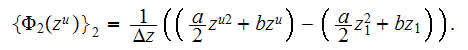
Obviously, this simple model having the closed analytical solution is of no technological interest. The effective conductivity coefficient for this one-phase medium is

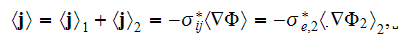
going further one gets using the homogeneous GO theorem (as for the one scale effective conductivity) on the left hand side of this equation

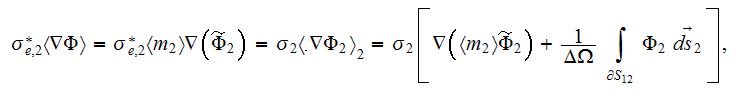
or after rewriting the operators the effective coefficient is equal

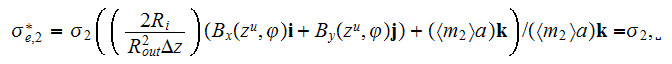
where

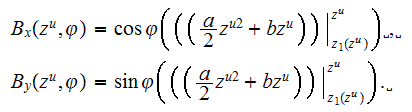
The result should not be unexpected as long as the physical conditions for the problem were simplified greatly - taken the diluted medium with no presence of the first phase (matrix) phenomena, allowing in this way the single phase modeling and the separate capillaries consideration. The homogeneous coefficient of conductivity and the morphology of the conductive phase secured the conditions well above a percolation threshold.

We might note, that this simplified example has an educational sense as to purportedly demonstrate the connection between scale's supposed problems solutions.

We believe that the complete analytical solution for the lower scale conjugate media electrostatics problem possible for this kind of morphologies (diluted capillaries), as it was done in thermal physics field.

Much more interesting the two-phase congugate problems were considered in works [37,47,53,54] see in -