Shortly it is this - Majumdar et al. (1995) produced microphotographs of thermal images that show the grain structure, visible in the topographical (morphology) image, and notes that "the grain boundaries appear hotter than within the grain. It is at present not clear why this occurs. - - The hot electrons collides with the lattice and transfer energy by the emission of phonons." The governing equations for non-magnetic medium they used to study the process were the one of conservation of electrons,

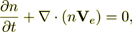    (1)

also the conservation of electron momentum,

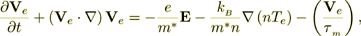    (2)

where the last term "is the collision and scattering term analogous to the Darcy term in porous media flow", conservation of electron energy,

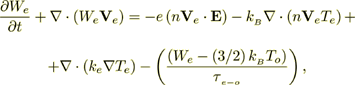    (3)

conservation of lattice optical phonon energy

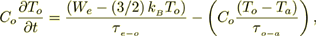    (4)

and conservation of acoustical energy

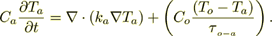    (5)

The last four equations have terms, the last term on the right hand side, that qualitatively reflect the collision and scattering rates in each process.

Here 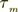is the electron momentum relaxation time, 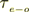is the electron optical relaxation time, 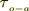is the optical acoustical relaxation time and 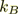is the Boltzmann's constant. In those equations assumed a scalar effective mass for the electrons m*.

The electric field is determined using the Gauss law equation written in terms of electric potential .

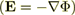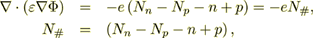    (6)

where is the dielectric constant of Si, N_n is the n-doping concentration, N_p is the p-doping concentration, p is the hole number density.

Here is the question, which might already asked by some disturbing students - "O.K. And what about having in this last equation also the kind of right hand side term which would reflect the effects of, well, "collision and scattering rates in each process?"

Seriously - Why not having the same kind of term(s) and in the electrostatics GE?

There was the need to maintain the approach to this set of equations, based on hydrodynamic interpretation of QM, as to the one which is the reasonable and recognizable in the physics related communities. Other note is that this could be an example of atomic scale governing equations set which is being understood as the descriptive for the particular atomic scale. Hearing from everywhere about that the scaling is the task for everyone we had liked to develop the two scale example being based on the firm mathematical ground of the scaling heterogeneous Ostrogradsky-Gauss kind theorems - the WSAM set of theorems for the governing equations for the upper scale heterogeneous media.

The advantage we have is that the rules have been set-up and that the governing equations obtained throughout this way are not as frivolous as by the using a "free-drive" approach.

We will construct the business of the second - the upper scale governing equations using the said above hydrodynamic plasma set of equations.

Non-Local Electrodynamics and Heat Transport in Superstructures as via the Hydrodynamic Interpretation of QM in Condensed Media

As we try to demonstrate here at this web site that the any reasonably formulated physical discipline governing equations can and may be the subject of the second (upper) or even greater scale strict physical and mathematical treatment, the following set of Upper Scale equations are applicable to the micrometer or hundred of micrometers scale material or device consideration.

As experimentalists know that the perfect crystalline structures exist mostly in the models, though the goal is to have some insight to situations when the medium can not be considered as homogeneous at any scale including the microscale level. For these circumstances, the governing field equations should be based on conservation equations for a heterogeneous medium, e.g. the HSP-VAT governing equations.

For particular reasons we skip here the few details of the derivation. Nevertheless, it can be a substantial journey from start to finish.

The HSP-VAT governing equations for heterostructures in a condensed medium will be found starting from the set of governing equations for a solid state electron plasma fluid. Phase averaging of the electron conservation equation (1) yields

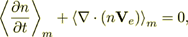    (7)

where <> m means averaging over the major phase of the material. The HSP-VAT final form for this equation is

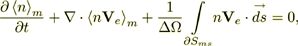    (8)

or

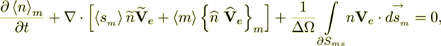    (9)

where 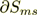is the "interface" (real or imaginable) of phases and scatterers.

It will be assumed that only immobile scatterers produce phase separation. This is not an essential restriction and is only taken to simplify the appearance of the equations and streamline the development.We recognize that defects and other scattering objects where processes are also occurring like non-major phases occur, but are not interested in them at this time because their volumetric fractions are very small and their importance is decreased by scattering of the fields in a major phase.

The electron fluid momentum transport equation can be written in two forms and the form influences the final appearance of the VAT equations. The first is

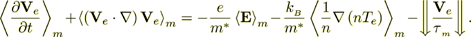    (10)

Using the transformation

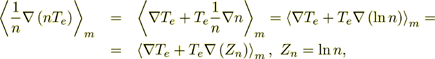    (11)

it can be written as

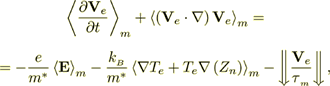    (12)

where the brackets 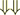define the problem uncertainty in the treatment of this relaxation term. Strictly speaking, this term should not be in this form and may not exist.

The same equation written in conservative form became

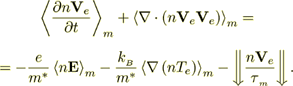    (13)

Using

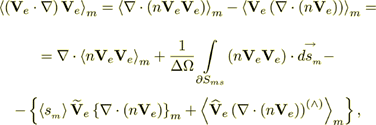    (14)

equation (12) can be written in the upper scale HSP-VAT form as

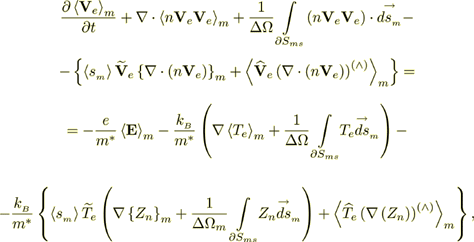    (15)

where the last term on the right hand side of (12), the scattering and collision reflection term, has been replaced by a number of terms, each reflecting interface specific phenomena including scattering and collision. Some manipulation of the convection terms of the conservative form of the momentum equation has been done to combine the forms of the equations of mass and momentum.

The second conservative form of the momentum equation is derived in the form

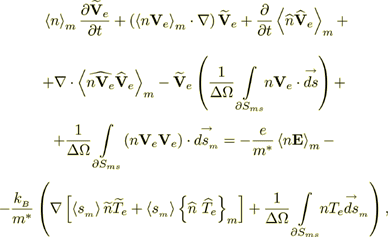    (16)

where a number of the integral terms are scattering and collision terms. There are other possible forms of the left hand side of the momentum equation - HSP-VAT equations that will not be pursued at this time.

The homogeneous volume averaged electron gas energy equation for a heterogeneous polycrystalline becomes

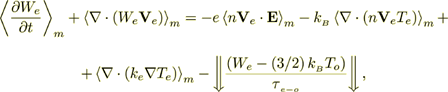    (17)

or

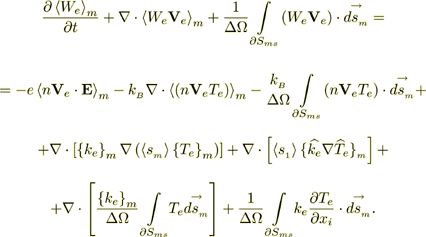    (18)

The integral terms again reflect scattering and collision that appear as a result of the heterogeneous media transport description.

The equation for longitudinal phonon temperature is

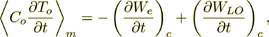    (19)

or

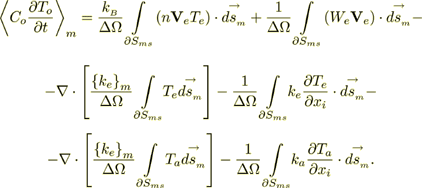    (20)

The equation of acoustical phonon energy is

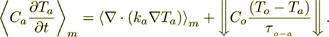    (21)

or

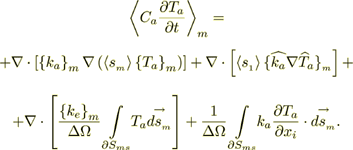    (22)

Describing phonon scattering and collision as an unsolved problem and as noted by Peterson (1994) "the complexity of this aspect of the problem precludes the relatively simple solution used in simulating rarefied gas flows."

Another kind of single phase equation for momentum transport of electronic fluid results for magnetized materials

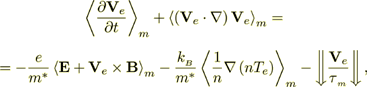    (23)

The VAT form of this equation is

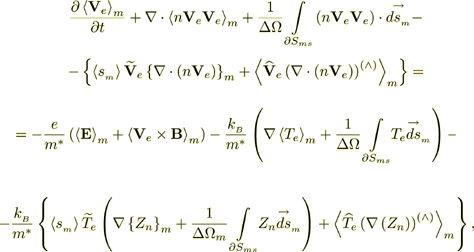    (24)

Now we will add here for the completeness of the picture the averaged nonlinear equation for the electric potential

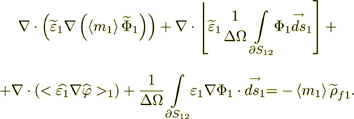    (25)

Here is the answer to that question above - Why not having the same kind of term and in the electrostatics GE? Yes, this should be also the term(s) reflecting the collective processes of local-non-local atomic scale electrodynamics with the "nano-micro-electrodynamics" of the lattice etc., etc.

The following remark is worth to read up as soon as we need to point out that - the second (Upper) scale governing averaged equations in this above set of HSP-VAT heterogeneous solid state plasma are only good if we know that the starting, the Lower scale equations were also correct. This we can not say about those above lower scale solid state plasma equations taken mostly following the paper by Majumdar et al. (1995). In these equations all the variables and the equations themselves are supposed to be as the already "averaged" ones, but they are not.

To have the more correct solid multicrystalline state HSP-VAT scaled mathematical model we have to accept the idea of AT LEAST the three scales taken into consideration. The Lower is the scale of really sub-atomic, inter-atomic size range, then the second (Intermediate) scale model that is within the single crystal (even imperfect crystal) and then the Upper (third) scale with the modeling equations for the solid state piece as it is assumed to be taken for continuum description.

See on the above remark in the subsection -

some more starting information for the scaled hierarchical physics for the solid (condensed) state theories and modeling are given in the below references.

We demonstrate here at this website in other section-sciences in any possible way that these kind of equations in spite of their horrible appearance are actually solvable, because of the due process. That any important term in the above equations can be closed and because of this closure the path opens to the calculation algorithms, as soon as the nanostructure (microstructure, molecular structure, etc.) of the medium is either known due to a research process or became assigned in accordance to the best knowledge of material's morphology (using any available microscope and morphology analyses tools), and cross-connection features of the supported two (or more) scale model.

References:

Travkin, V.S., "What Classical Mechanics of XVIII Provided in XX Has Done Wrong to the Base of Mechanical Science Including the Classical Mechanics of Continuum Particles and Conventional Orthodox Homogeneous Particle Physics", http://travkin-hspt.com/rottors/classmechwrong/classmechwrong.htm, (2014)

Travkin, V.S.,"The Major Forces Have Been Missing From Governing Equations for Dynamics of Sub-atomic and Continuum Particles, Bodies in XVIII - XX ", http://travkin-hspt.com/rottors/forcemissing/forcemissing.htm, (2014)

Travkin, V. S., "Electrodynamics 2 - Elements 3P (Polyphase-Polyscale-Polyphysics)," http://travkin-hspt.com/eldyn2/index.htm

Travkin, V. S., "What's Going on in Particle Physics with Homogeneous Approach? How we Can Up-scale from the Sub-Atomic to the Continuum Mechanics? By MD it is the False Method (via the Homogeneous MD) and Even a False Math." http://travkin-hspt.com/parphys/right.htm

Travkin, V. S., "Particle Physics - Heterogeneous Polyscale Collectively Interactive," http://travkin-hspt.com/parphys/index.htm

Travkin, V. S., "Quantum Mechanics-Why Not? What's Wrong? Some of the History," http://travkin-hspt.com/parphys/qmnot1/qmnot1.htm

Travkin, V. S., "Quantum Mechanics Other Theories (de Broglie--Bohm Theory, etc.) - Why Not 2? What's Wrong?," http://travkin-hspt.com/parphys/qmnot2/qmnot2.htm

Travkin, V. S., "Particle Physics 2 - Elements 2P," http://travkin-hspt.com/parphys2/index.htm

Travkin, V. S., "Magnetism. Ferromagnetism," "http://travkin-hspt.com/fermag/index.htm;"

Majumdar, A., Lai, J., Luo, K., and Shi, Z., "Thermal Imaging and Modeling of Sub-Micrometer Silicon Devices", in Proc. Symposium om Thermal Science and Engin. in Honor of Chancellor Chang-Lin Tien, pp. 137-144, (1995).

Peterson, R.B., "Direct Simulation of Phonon-Mediated Heat Transfer in a Debye Crystal", J. Heat Transfer, Vol. 116, No. 4, pp. 815-822, (1994).

Travkin, V.S. and Catton, I. Porous Media Transport Descriptions - Non-Local, Linear and Non-linear Against Effective Thermal/Fluid Properties//Advances in Colloid and Interface Science. 1998. V.76-77. P.389-443.

Travkin, V.S. and Catton, I. Transport phenomena in heterogeneous media based on volume averaging theory// Advances in Heat Transfer. (New York, Academic Press, 2001. Vol. 34.). P.1-144.

Travkin, V. S. and Ponomarenko, A. T., "Electrodynamic Equations for Heterogeneous Media and Structures on the Length Scales of Their Constituents", Inorganic Materials, Vol. 40, Suppl. 2, pp. S128 - S144, (2004).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications -1," Journal of Alternative Energy and Ecology, No. 3, pp. 9-19, (2005).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 2," Journal of Alternative Energy and Ecology, No. 4, pp. 9-22, (2005).

Travkin, V. S. and Ponomarenko, A. T., "The Non-local Formulation of Electrostatic Problems for Sensors Heterogeneous Two- or Three Phase Media, the Two-Scale Solutions and Measurement Applications - 3," Journal of Alternative Energy and Ecology, No. 5, pp. 34-44, (2005).

Travkin, V.S., Nanotechnologies - General Concept for Pretty Large Amount of Pretty Small Gadgets Embedded Into Something and Consequences for Design and Manufacturing, http://travkin-hspt.com/nanotech/index.htm, (2006)

Travkin, V.S., Electrodynamics 2 - Elements 3P (Polyphase-Polyscale-Polyphysics), http://travkin-hspt.com/eldyn2/index.htm, (2013)

Travkin, V.S. and Bolotina, N.N., "The Classical and Sub-Atomic Physics are the Same Physics," http://travkin-hspt.com/parphys/pdf/51_PrAtEd-QM-Ref-2HSPT.pdf, (2013)

Travkin, V.S., Particle Physics - Heterogeneous Polyscale Collectively Interactive, http://travkin-hspt.com/parphys/index.htm, (2011)

Travkin, V.S., Particle Physics (Particle Physics 2). Fundamentals, http://travkin-hspt.com/parphys2/index.htm, (2013)

Travkin, V.S., Nuclear Physics Structured. Introduction, http://travkin-hspt.com/nuc/index.htm, (2006-2013)

Travkin, V.S., What's Wrong with the Pseudo-Averaging Used in Textbooks on Atomic Physics and Electrodynamics for Maxwell-Heaviside-Lorentz Electromagnetism Equations, http://travkin-hspt.com/eldyn/maxdown/maxdown.htm, (2009)

Travkin, V.S., Incompatibility of Maxwell-Lorentz Electrodynamics Equations at Atomic and Continuum Scales, http://travkin-hspt.com/eldyn/incompat/incompat.htm, (2009)

Travkin, V.S., Experimental Science in Heterogeneous Media, http://travkin-hspt.com/exscience/index.htm, (2005)

Travkin, V.S., Statistical Mechanics Homogeneous for Point Particles. What Objects it Articulates? http://travkin-hspt.com/statmech/index.htm, (2014)

Travkin, V.S., Solid State Polyscale Physics. Fundamentals, http://travkin-hspt.com/solphys/index.htm, (2014)

Travkin, V.S., "Two-Scale Three-Phase Regular and Irregular Shape Charged Particles (Electrons, Photons) Movement in MHL Electromagnetic Fields in a Vacuum0 (Aether)," http://travkin-hspt.com/http://travkin-hspt.com/parphys2/abstracts/twoparticlesshort-ab.htm

Travkin, V.S. and Bolotina, N.N., "Two-Scale Two-Phase Formation of Charged 3D Continuum Particles - Sphere and Cube From Electrons in a Vacuum0 (Aether). An Example of Scaleportation of Charge from the Sub-Atomic to Continuum Charged Particles, Conventional MD Cannot be Applied," http://travkin-hspt.com/http://travkin-hspt.com/parphys2/abstracts/subtocontin-ab.htm

Travkin, V.S. and Bolotina, N.N., "One Structured Electron in an Aether (Vacuum0) Electrodynamics, Many Electrons in an Aether Fixed in Space - the Upper Scale Galilean Electrodynamics ," http://travkin-hspt.com/http://travkin-hspt.com/parphys/abstracts/stillelectrons-ab.htm

Travkin, V.S. and Bolotina, N.N., "Electrons and CMBR (Cosmic Microwave Background Radiation) Flux of Photons in a Vacuum0 (Aether) - Two-Scale Galilean Theory ," http://travkin-hspt.com/parphys/abstracts/elcmbr-ab.htm

and in publications mentioned above.