For any acoustical problem the one of initial questions arises is - What are the medium characteristics this problem is considered for?
We present and discuss this issue for many times in the different pages of this web site. Nevertheless, for each time for a new (actually just different) physical science, discipline, this is still an unavoidable question. If the medium is solidly homogeneous - that is the area for conventional textbooks acoustics.
Another situation if the medium has features, properties of heterogeneity - like, multy-phaseness, interphase transitions, physico-chemical peculiarities at the interfaces, etc. then we need honestly try to face the whole new situation. Just few aspects among great number are given here
in this website in the section -
If the medium, which is being set-up for an acoustical problem, known as being heterogeneous, or dependent from the lower (smaller) or larger scale physical phenomena,
then its physical and mathematical descriptions need to be considered and constructed in a way incorporating the interdependence of higher (larger) scale descriptions and mathematical modeling into the lower and vice versa. Also, we need to remember that the acoustics as a field is not in any regard something outstandingly different then other physical disciplines.
Acoustic wave propagation in heterogeneous media and specifically in porous media has been an evolving field since the
pioneering work of Rayleigh (1907). The absence of good physical and mathematical theories is the reason that much of today's
research is still following the direction outlined by Rayleigh. Present research seems to be following one of three paths. One of
them is represented by experimental studies of available materials subject to incident acoustic fields. Among this work is that
of Delany and Bazley (1970), Attenborough (1985), and Voronina (1997) just to name randomly few of the relevant studies.
The second path is the one where the theoretical basis of experimental data reduction is insufficient, leading to the use of
simplistic physical models and models developed with a narrow focus on modeling some features of the phenomena and to represent
only the more evident characteristics. This path is represented, for example, in studies by Allard and Champoux (1992), Morse and Ingard
(1968), Johnson et al. (1987), and Wilson (1993, 1997). The need for a model describing thermal and momentum transport with
acoustic wave propagation was recognized many years ago in number of papers (Johnson et al., 1987; Wilson, 1993, 1997, Biot, 1956a,b; Allard, 1993, etc.).
Still, the models for these processes are constructed based on the present homogeneous media kind of thinking, see for example, the work by Buckingham (1997)
that is based on the equation
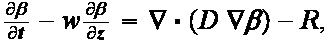
where 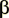 is the bubble concentration and
is the bubble concentration and 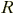 is the
net rate of loss of gas fraction in the sea water.
is the
net rate of loss of gas fraction in the sea water.
It is now more than 10 years from 1998 when the HSP-VAT concepts, methodology, and mathematics for the acoustics modeling in heterogeneous
media have been developed and told about at few meetings in the US, Italy, other countries based on our studies in fluid mechanics, heat transport and other fields. For the linear and nonlinear acoustical wave propagation in heterogeneous and porous media and for the problem with the two media - for example,
when propagation happens to be in a core of channel which is the void area and with the some specified morphology, as well as for the open morphology layers on the wall.
Improvements to the widely used experimental correlations of Delany and Bazley (1970), and models by Biot (1956a,b)
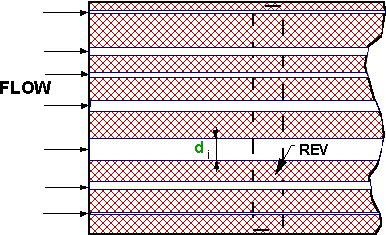
Capillary morphology model of porous medium: a bundle of
parallel pores, all of different diameters - Straight Parallel Pores Morphology (SPPM), embedded in a solid
Allard (1993), and Takahashi (1989) can be demonstrated using the results of the Hierarchical Scaled Physics - Volume Averaging Theory (HSP-VAT) based studies for acoustics transport phenomena in heterogeneous media.
It would be appropriate to spell out here few words on the priority of the non-local, two-scale, linear acoustics and electrodynamics HSP-VAT governing equations and concepts developments. The first time conceptual solutions and governing equations for heterogeneous media acoustics and electrodynamics
HSP-VAT had been developed in 1997-98, and some information was shared with few companies, including NASA and Naval Postgraduate School (Monterey, CA). See more details on priority of these advancements in "Electrodynamics" section of this website -
We would like to state here what is said many times in public at presentations and lectures that there is - No way to solve or analyze correctly the
Heterogeneous Acoustics problems if Homogeneous Acoustics Tools Applied, because:
1) You can not find (calculate) the sought after Upper Scale bulk
characteristics such as - neither the reflection and absorption coefficients
nor the effective density
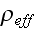 and bulk modulus
and bulk modulus
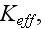 etc.
etc.
2) You can not solve the phase specific and phase averaged acoustic problem
correctly.
3) You can not solve this one of the simplest problems - the SPP morphology (SPPM)
for the Upper (averaged fields) scale even when it is the one pore diameter
medium - solutions by Biot, Allard, etc. are for the Lower scale characteristics only.
If only one diameter of pores (channels) is different from others or varying one
from another and along the single coordinate of axis of pores then the problem
is untreatable in Homogeneous acoustics.
Not for the fluid (air) phase wave propagation nor, of course, for the
two-phase problem stated.
4) You can not solve a one HtA problem where (when) the physics on the
boundary surfaces is taken as for the homogeneous media - because there are
the different BC should be applied for heterogeneous problems. At the
meantime, the homogeneous acoustics does not know - How to define and
introduce those BC.
For example, when a silencer (liner) design is being considered - the only
tools they continue to rely upon is the experimental work-studies with the
data reduction models as for a "Luna orbiter"?
There exists no one more or less realistic heterogeneous conceptual, modeling, technical approach to
this problem,
but used right now the one scale homogeneous models.
From time to time we will publish in this section of the website some interesting Heterogeneous Acoustics (HtA) results for educational purposes and for advertisement.
REFERENCES
These references below by no means should be considered as the most important or valuable?
No way - these are the samples of the wrongdoing in Heterogeneous Acoustics, nothing more.
But Biot, Brekhovskikh, Morse, and Ingard works are of well known respect although anyway of homogeneous physics.
Allard, J.-F. and Champoux, Y. , "New Empirical Equations for Sound Propagation in Rigid
Frame Fibrous Materials", J. Acoust. Soc. Am., Vol. 91, pp. 3346-3353, (1992)
Allard, J.-F., Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials,
edited by Elsevier Applied Science, Elsevier Science, London, (1993)
Attenborough, K. , "Acoustical Characteristics of Rigid Fibrous Absorbents and Granular Materials",
J. Acoust. Soc. Am., Vol. 73, No.3, pp. 785-799, (1983)
Attenborough, K. , "Acoustical Impedance Models for Outdoor Ground Surfaces", J. Sound Vibr.,
Vol. 99, pp. 521-544, (1985)
Biot, M.A., "Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid.
I Low Frequency Range", J. Acous. Soc. Am., Vol. 28, No. 2, pp. 168-178, (1956a)
Biot, M.A., "Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid.
II Higher Frequency Range", J. Acous. Soc. Am., Vol. 28, No. 2, pp. 179-191, (1956b)
Brekhovskikh, L.M., "Waves in Layered Media," Moscow, Nauka, (1973)
Brekhovskikh, L.M., "Waves in Layered Media," New York, Academic press, (1960)
Brekhovskikh, L.M. and Goncharov, V., Mechanics of Continua and Wave Dynamics, Wave Phenomena, Vol. 1, Springer-Verlag, Berlin, 1994, (1998)
Brekhovskikh, L.M. and Godin, O.A., Acoustics of Layered Media I. Plane and Quasi-Plane Waves, Wave Phenomena, Vol. 5, Springer-Verlag, Berlin, (1990)
Brekhovskikh, L.M. and Godin, O.A., Acoustics of Layered Media II. Point Source and Bounded Beams, Wave Phenomena, Vol. 10, Springer-Verlag, Berlin, (1999)
Brekhovskikh, L.M. and Lysanov, Yu.P., Fundamentals of Ocean Acoustics. 2nd Ed., Wave Phenomena, Vol. 8, Springer-Verlag, Berlin, (2003)
Buckingham, M.J. , "Sound Speed and Void Fraction Profiles in the Sea Surface Bubble Layer", Appl. Acoust., Vol. 51, No.3, pp. 225-250, (1997)
Champoux, Y. and Stinson, M.R., "On Acoustical Models for Sound Propagation in Rigid Frame Poros Materials and the Influence of Shape Factors", J. Acoust. Soc. Am., Vol. 92, No.2, pp. 1120-1131, (1992)
Delany, M.A. and Bazley, E.N., "Acoustic Properties of Fibrous Absorbent Materials", Appl. Acoust., Vol. 3, pp. 105-116, (1970)
Johnson, D.L., Koplik, J., and Dashen, R., "Theory of Dynamic Permeability and Tortuosity in Fluid-Saturated Porous Media", J. Fluid Mech., Vol. 176, pp. 379-401, (1987)
Kim, J.-H., "Stochastic Turning Point Problem in a One-Dimensional Refractive Random Multilayer", SIAM J. Appl. Math., Vol. 56, No. 4, pp. 1164-1180, (1996)
Lahey, R.T., Jr., Park, J-W., and Drew, D.A., "The Analysis of Void Waves in Two-Phase Flow",
Nucl. Eng. Des., Vol. 141, pp. 203-224, (1993)
Morse, P.M. and Ingard, K.U., Theoretical Acoustics, McGraw-Hill, Princeton, NJ, (1968)
Rayleigh, J.W.S., "On the Dynamical Theory of Gratings", Proc. Royal Soc. London, A79, pp. 399-416, (1907)
Stinson, M.R., "The Propagation of Plane Sound Waves in Narrow and Wide Circular Tubes, and Generalization to Uniform Tubes of Arbitrary Cross-Sectional Shape", J. Acoust. Soc. Am., Vol. 89, No.2, pp. 550-558, (1991)
Takahashi, D., "Excess Sound Absorption due to Periodically Arranged Absorptive Materials", J. Acoust. Soc. Am., Vol. 86, pp. 2215-2222, (1989)
Voronina, N., "An Empirical Model for Rigid Frame Porous Materials withHigh Porosity", Appl. Acoust., Vol. 51, No. 2, pp. 181-198, (1997)
Wilson, D.K., "Relaxation-Matched Modeling of Propagation through Media, Including Fractal Pore Straucture", J. Acoust. Soc. Am., Vol. 94, No.2, pp. 1136-1145, (1993)
Wilson, D.K., "Simple, Relaxational Models for the Acoustical Properties of Porous Media", Appl. Acoust., Vol. 50, No. 3, pp. 171-188, (1997).
Yamamoto, T., "Acoustic Propagation in the Ocean with a Poro-Elasric Bottom", J. Acoust. Soc. Am., Vol. 73, No.5, pp. 1587-1596, (1983)
Yamamoto, T. and Turgut, A., "Acoustic Wave Propagation through Porous Media with
Arbitrary Pore Size Distributions", J. Acoust. Soc. Am., Vol. 83, No.5, pp. 1744-1751, (1988)
Zwikker, C. and Kosten, C.W., Sound Absorbing Materials, Elsevier, New York, (1949)
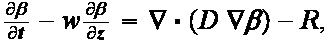
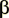 is the bubble concentration and
is the bubble concentration and 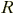 is the
net rate of loss of gas fraction in the sea water.
is the
net rate of loss of gas fraction in the sea water.

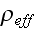 and bulk modulus
and bulk modulus
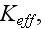 etc.
etc.