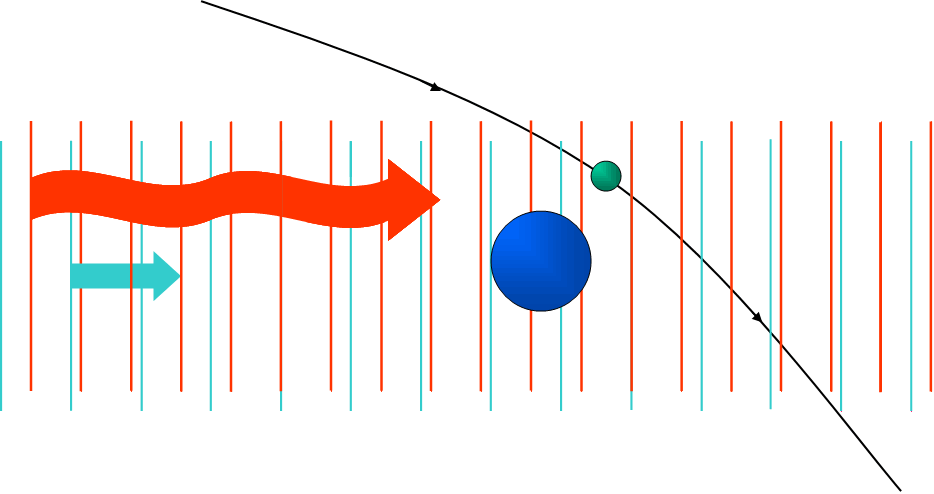
Enhancement and Absorption of Two Electromagnetic Waves During Single Electron Scattering on the Nucleus
(concise version of the study)
Tsibulnik V.A.
(translation by N.N. Bolotina)
It is well known that light going through the matter (glass, water, air and etc.) is weakening. Most of us don't know and don't even think why it is so, but this is an experimental fact, which is difficult to have any doubt about. However, it turned out that under certain circumstances there is a possibility of amplification of the electromagnetic waves when they are going through the matter due to the energy of this matter! To be more specific, laser radiation, going through the plasma, where the processes of the dispersion of the electrons on the nuclei are going, may intensify!
The theory of strong electromagnetic radiation is dealing with this problem. This theory has been widely developed in some recent years due to the creation of the lasers and their quick progress in power increase. In last few years it became possible to check a lots of theories and formulae by experimenting as a result of creation of compact high-power lasers.
It should be mentioned that quantum-electrodynamic processes in the field of the plane monochromatic electromagnetic wave, which presents the laser radiation, have been studied by such famous scientists as Volkov, Delone, Krainov, Fedorov and etc. for quite a long time. As early as in 70-80s Borisov, Zhykovskiy, Karapetyan, Fedorov, Krainov, Roshchupkin and oher scientists studied the processes of spontaneous and enforced (stimulated) collision radiation during the dispersion of the electron on the nucleous in the field of the plane electromagnetic wave in different particular cases of energies of the electron and intensities of the wave. However, lately scientists are more interested in studying elementary quantum processes in superposition of several laser fields, for example forced collision radiation and absorption during dispersion of the electron on the nucleous with the two plane electromagnetic waves. While studying this process Roshchupkin S.P. found out a new interference effect connected to the correlated radiation and absorption of the electron for the equal number of photons of both waves. More solid research of this effect shows that light waves when going through the matter may be intensified!
In a strong field of radiation effects connected with absorption or releasing into a wave of several quantum at once that play a vital role. Using the so-called Volkov's solution for wave functions, describing the state of real particles, it's possible to calculate the probabilities of different processes in the field of the wave. The mentioned method of calculation of interaction with the intensive field of the wave is used in many researches, as it allows to get general solution's formulae correctly, when there are arbitrary intensions of the wave. This mehod of examination of processes in the intensive electromagnetic field is a half-classic - the falling wave is considered as a classic field, and all the rest of the particles (electron, absorbed and radiated quantum) are considered as via the quantum-mechanical notions. Such description is justified as the radiation of the really acting sources is practically always corresponding to a large number of photons.

While studying the process of enforced (stimulated) collision radiation in the field of the
external light waves, it's essential to differentiate the spontaneous and
forced radiation. In spite of the commonness of the nature, the spontaneous
radiation may occur on different frequencies and in different directions,
whereas the forced radiation (absorption) occurs only at the frequency of the
external electromagnetic wave. The differential cross-section of the process
for the forced radiation of the photons to the external field while occurs we
will take as the

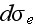 (emission) and the differential cross-section for which the force absorption
of the photons out of the external wave occurs - as the
(emission) and the differential cross-section for which the force absorption
of the photons out of the external wave occurs - as the

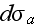 absorption. It makes sense to take such a concept as the total differential
cross-section
absorption. It makes sense to take such a concept as the total differential
cross-section

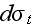 (total)
if we are interested only in increase or decrease of the number of photons:
(total)
if we are interested only in increase or decrease of the number of photons:
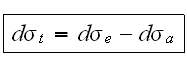
The total differential cross-section is connected to the change of the number of photons of the external wave, i.e. with its amplification or attenuation.
------------
We will write down the Dirac's equation in the field of the plane wave for
finding differential cross-sections of radiation and absorption:
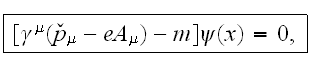 where
where

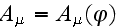 ,
,

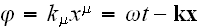 .
.
This equation was first solved by D. Volkov in 1937 and was widely adopted at the beginning of 60s due to the creation of the laser technology, as Volkov's solution models the field of the laser. At present time there is a whole part in physics - the laser physics, which studying the interaction of the laser radiation with a matter using both experimental and theoretical options.
Let's write down this solution briefly.
We can multiply the Dirac's equation by

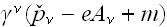 :
:
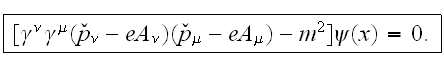
And should consider that
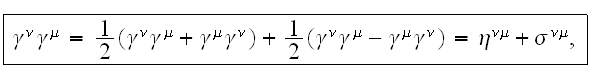 then after the transformations
then after the transformations
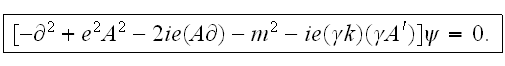
Thus, the Dirac's equation transforms to the differential equation of the
second order. We should mention that this equation has an excess solution. The
solution we search in the form of
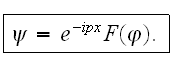 We can substitute this expression into the differential equation and after
transformations we get:
We can substitute this expression into the differential equation and after
transformations we get:
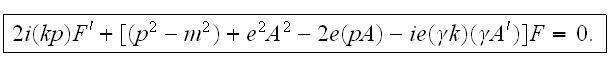
In this solution the 4-vector

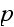 is polysemantic and we can assign an additional condition for it, for example
is polysemantic and we can assign an additional condition for it, for example

From this it follows that while turning off the external field 4-vector has a
physical sense of the 4-impulse of a free electron
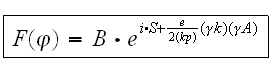
where
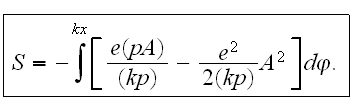 We take the constant as
We take the constant as
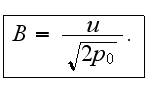 All the degrees of
All the degrees of

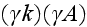 those higher than one are equal to zero as soos as
those higher than one are equal to zero as soos as
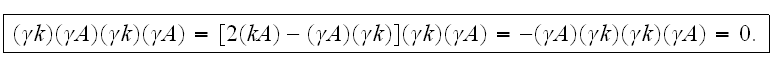 According to that we can replace
According to that we can replace
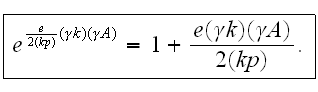 The final Volkov's solution is:
The final Volkov's solution is:
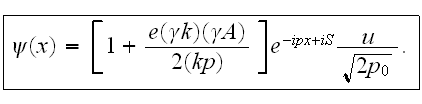 Note, that while turning off the external field the Volkov's function
transforms into the solution of Dirac's equation for a free electron. From
this it follows that
Note, that while turning off the external field the Volkov's function
transforms into the solution of Dirac's equation for a free electron. From
this it follows that

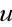 - is the byspin of the free electron and we can put the condition of
normalization on it
- is the byspin of the free electron and we can put the condition of
normalization on it
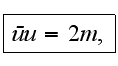
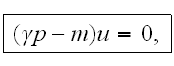
which allows to avoid the excess solution.
In this way we've got an expression for Volkov's function which is the solution of Dirac's equation in the field of the plane electromagnetic field. This expression will allow us to find the differential radiations of the processes of forced (stimulated) radiation and absorption of the photons.
---------------------
At first we examine the passing of the process in the field of one elliptically polarized wave for which 4-potential of the electromagnetic wave is:
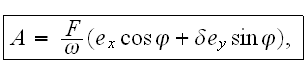
where

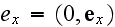 ,
,

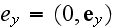 -- the 4-vectors of wave polarization,
-- the 4-vectors of wave polarization,

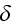 -- the parameter of wave ellipticity, and
-- the parameter of wave ellipticity, and

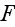 and
and

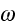 -- are the voltage and the frequency of a wave; the
argument
-- are the voltage and the frequency of a wave; the
argument 
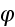 has an expresion
has an expresion

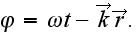
Expanding the solution of Dirac's equation into the Fourier series we get:
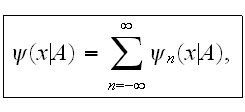
where partial wave functions

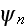 ,
responding to various processes of forced radiation and absorption of the
electron wave
,
responding to various processes of forced radiation and absorption of the
electron wave

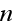 photons look like:
photons look like:
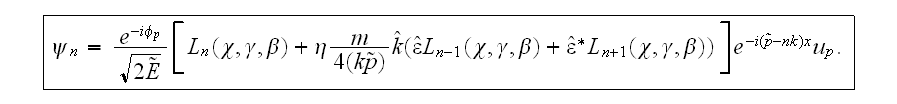
Here

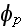 -- the phase, which is independant of summation index,
-- the phase, which is independant of summation index,

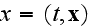 -- the 4-vector,
-- the 4-vector,

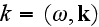 -- the 4-impulse of the external field photon,
-- the 4-impulse of the external field photon,

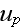 -- the Dirac's byspin, where the expression with roofs mean scalar products of
Dirac's matrixes
-- the Dirac's byspin, where the expression with roofs mean scalar products of
Dirac's matrixes

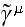 (
(
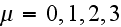 )
with corresponding 4-vectors
(
)
with corresponding 4-vectors
(
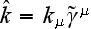 ),
4-vector
),
4-vector

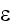 and the 4-quasi-impulse
and the 4-quasi-impulse

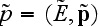 are accordingly equal
are accordingly equal
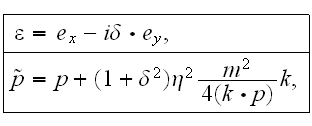
where the relativist-invariant parameter

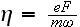 is numerically equal to the ratio of the field's work on the wave length to
the electron's ground energy and characterizes the wave intensity.
is numerically equal to the ratio of the field's work on the wave length to
the electron's ground energy and characterizes the wave intensity.
The function

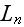 depends on three relativist-invariant parameters
depends on three relativist-invariant parameters

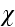 ,
,

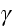 ,
,

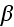 and has the following appearance:
and has the following appearance:
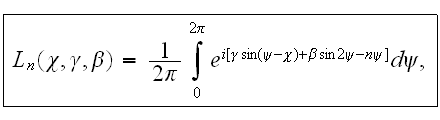
where
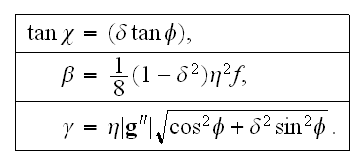
Here

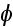 -- is the angle between
-- is the angle between

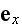 and parallel to the plane surface
and parallel to the plane surface

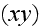 component
component

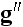 of the vector
of the vector

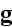 ,
and the 4-vector
,
and the 4-vector

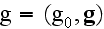 and the relativist-invariant function
and the relativist-invariant function

 have the following appearance:
have the following appearance:
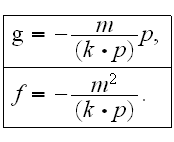
We should mention, that these functions

 may be developed using Bessel's functions of integer-valued order
may be developed using Bessel's functions of integer-valued order

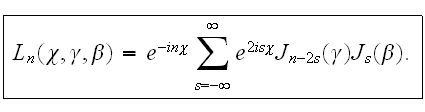
Out of this integral presentation

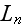 we see that this function is the Fourier
we see that this function is the Fourier

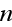 -coefficient
for
-coefficient
for
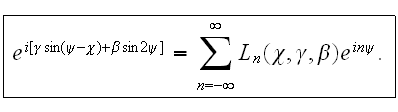
It's essential to stress out that these functions

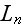 determine the probability of multiphoton processes in the field of one plane
electromagnetic wave.
determine the probability of multiphoton processes in the field of one plane
electromagnetic wave.
---------------
And now we complicate the task and choose the 4-potential of the external
electromagnetic field as a sum of two plane waves propagating along the axis

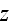 :
:
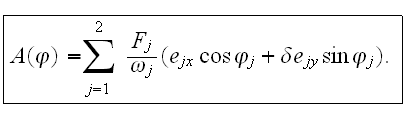
We expand Volkov's solution in this field in a double Fourier series:
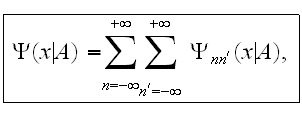
where partial wave functions

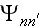 ,
corresponding to various processes of enforced radiation and absorption by the
electron the
,
corresponding to various processes of enforced radiation and absorption by the
electron the

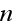 photons of the first wave and
photons of the first wave and

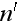 photons of the second wave have the apperance of:
photons of the second wave have the apperance of:
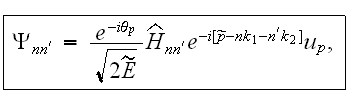 where
where
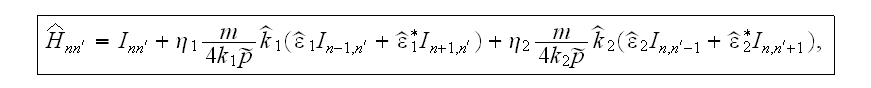
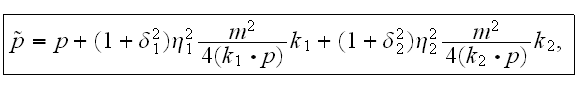
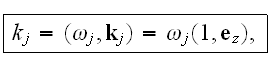
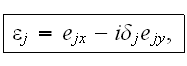
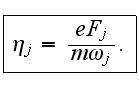
Here

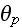 -- the phase independant of summation index,
-- the phase independant of summation index,

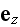 -- the single vector along the direction of both waves movements.
-- the single vector along the direction of both waves movements.
The function

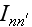 depends on the ten relativist-invariant parameters:
depends on the ten relativist-invariant parameters:
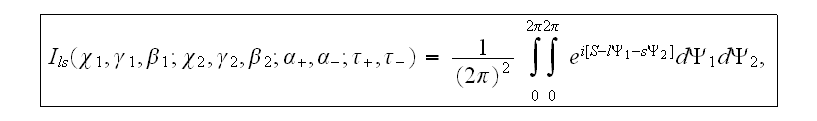
where

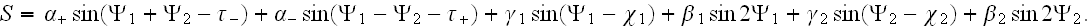
Here the parameters of two waves

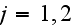 were taken in the following way:
were taken in the following way:
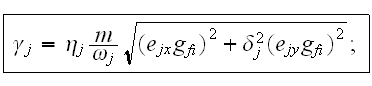
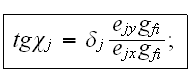
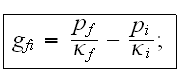
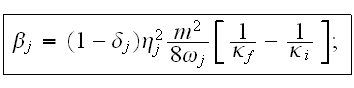
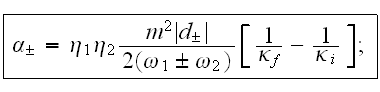
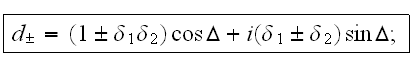
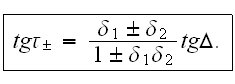
Here

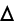 -- - the angle between
-- - the angle between

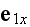 and
and

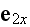 ,
,

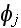 -- the angle between
-- the angle between

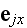 and the parallel to the plane
and the parallel to the plane

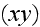 of vector component
of vector component

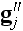 of the vector
of the vector

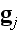 .
The 4-vector
.
The 4-vector

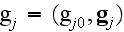 and relativist-invariant functions
and relativist-invariant functions

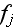 и
и

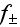 have the appearance
have the appearance
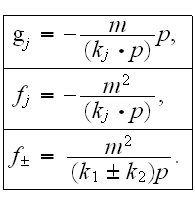
Out of this integral presentation we see that the functions

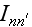 are coefficients of Fourier function
are coefficients of Fourier function
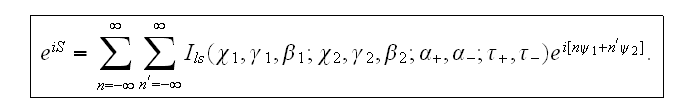
It's essential to mention that these functions

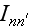 determine the probability of multiphoton processes in the field of two plane
electromagnetic waves.
determine the probability of multiphoton processes in the field of two plane
electromagnetic waves.
-----------------
Now with the help of the obtained dependencies we can find the differential cross-section of the enforced collision radiation while the dispersion of the electron on the nucleous in the field of these two electromagnetic waves in the following way:
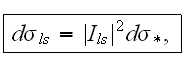
where the differential Mott section

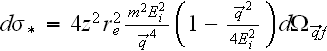 ,
and determined that
,
and determined that

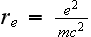 ,
,

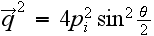 .
.
And as follow we have the opportunity to find numerically the total
differential cross-section normalized by the Mott cross-section for various
intensities

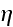 ,
frequencies
,
frequencies

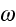 and polarizations
and polarizations

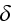 of the waves.
of the waves.
We come back to finding the total differential cross-sections of radiation and absorption:
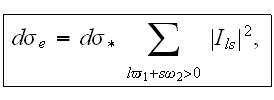
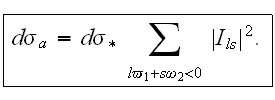
We've studied the average cross-section over the angles of incoming electron:
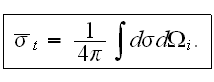
The so-called interference and non-interference areas were studied separately. Interference area is considered as an area where the dispersion occurs in the plane formed by the impulse of the initial electron and the wave vector. At the same time azimuth direction angles of the electron movement in the initial and final states are equal and polar - are in the ratio:
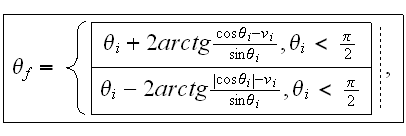
where

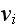 - the initial speed of the electron.
- the initial speed of the electron.
Some results of calculations we can show in the form of the following basic diagrams:
1) the dependence of the average total differential cross-section

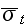 on the initial speed of the electron in the non-interference area:
on the initial speed of the electron in the non-interference area:
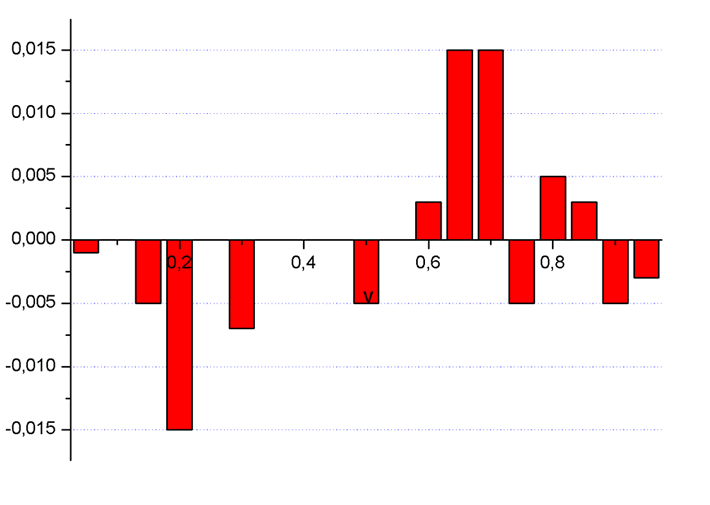
and 2) the dependence of the average total differential cross-section on the initial speed of the electron in the interference area:
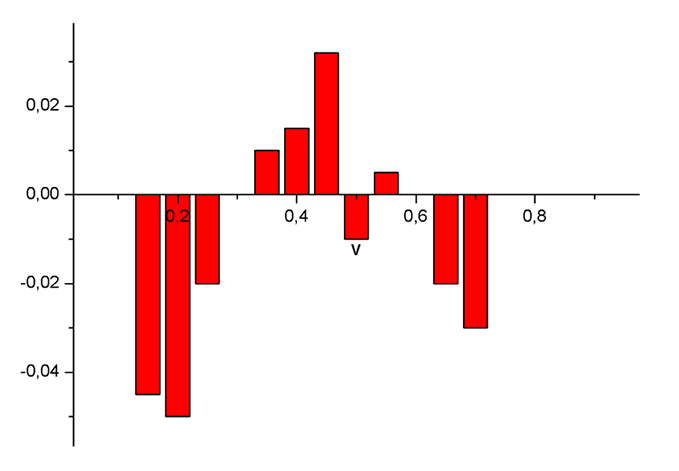
We see that both in the interference and non-interference areas absorption in general predominates over radiation as the radiation weakens, however there exist the certain areas of the initial speeds of the electron where radiation predominates over absorption and as follows the light intensifies. Comparison of absolute quantities of the total cross-section in the interference and non-interference areas shows that amplification of the electromagnetic waves usually occurs in the interference area and probability of that event almost 3 times higher than the corresponding probability in the non-interference area.
Thus, our aim is achieved - we have shown that for certain conditions the laser rays going through the matter can amplify! This is a completely new result opening a new direction of research in physics of interaction of intensive electromagnetic radiation with matter. And undoubtedly, this result will open new horizons of application the examined effects in technology and engineering.
References - are placed at the end of the Russian text
the Russian language text of the same study
Enhancement and Absorption of Two Electromagnetic Waves During Single Electron Scattering on the Nucleus (in Russian)
Tsibulnik V.A.
Всем извесно, что свет, проходя через вещество (стекло, вода, воздух и т.п.), ослабляется. Многие из нас не знают и даже не задумываются, почему это так, но это экспериментальный факт, который трудно подвергать сомнению. Однако оказывается, что при определённых условиях существует возможность усиления световых волн при прохождении через вещество за счёт энергии этого вещества! Если говорить более конкретно, то лазерное излучение, проходя через плазму, где идут процессы рассеяния электронов на ядрах, может усиливаться!
Этой проблемой занимается теория взаимодействия интенсивного электромагнитного излучения с электронами, которая получила в последние годы широкое развитие в связи с созданием лазеров и значительным и быстрым прогрессом в увеличении их мощности. В последние несколько лет появилась возможность проверки многих теорий и формул экспериментально, в связи с созданием компактных лазеров высокой мощности. Например, серия экспериментов по проверке квантовой электродинамики проводится группой МакДональда на лазере SLAC.
Следует отметить, что квантово-электродинамические процессы в поле плоской монохроматической электромагнитной волны, которой является лазерное излучение, изучаются достаточно давно такими известными учёными, как Волков, Делоне, Крайнов, Фёдоров и др. Ещё в 70-80 гг. Борисов, Жуковский, Карапетян, Фёдоров, Крайнов, Рощупкин и другие учёные изучали процессы спонтанного и вынужденного тормозного излучения при рассеянии электрона на ядре в поле плоской электромагнитной волны в различных частных случаях энергий электрона и интенсивностей волны. Однако в последнее время всё больше вызывает интерес изучение элементарных квантовых процессов в суперпозиции нескольких лазерных полей, например вынужденное тормозное излучение и поглощение при рассеянии электрона на ядре в присутствии двух плоских электромагнитных волн. При изучении этого процесса Рощупкиным С.П. был обнаружен новый интерференционный эффект, связанный с коррелированныи излучением и поглощением электроном равного числа фотонов обеих волн. Более глубокое исследование этого эффекта и приводит нас к возможности усиления световых волн при прохождении через вещество!
В сильном поле излучения существенную роль играют эффекты, связанные с поглощением из волны или испусканием в волну сразу нескольких квантов. Используя так называемое решение Волкова в качестве волновых функций, описывающих состояние реальных частиц, можно вычислить вероятности различных процессов в поле волны. Указанный метод учета взаимодействия с интенсивным полем волны применяется во многих работах, т.к. позволяет получить общие формулы, справедливые при произвольных интенсивностях волны. Данный метод рассмотрения процессов в интенсивном электромагнитном поле является полуклассическим --- падающая волна рассматривается как классическое поле, а все остальные частицы (электрон, поглощенные и излученные кванты) рассматриваются квантовомеханически. Такое описание оправдано,так как излучение реально действующих источников практически всегда соответствует большому числу фотонов.

При
рассмотрении
процесса
вынужденного
тормозного
излучения в
поле внешних
световых
волн,
необходимо
различать
спонтанное и
вынужденное
излучение.
Несмотря на
общность
природы,
спонтанное
излучение
может
происходить
на различных
частотах и в
различных
направлениях,
в то время
как
вынужденное
излучение
(поглощение)
происходит
только на
частоте
внешней
электромагнитной
волны.
Дифференциальное
сечение
процесса,
при котором
происходит
вынужденное
излучение
фотонов во
внешнее поле
обозначим

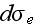 (emission),
а
дифференциальное
сечение, при
котором
происходит
вынужденное
поглощение
фотонов из
внешней
волны ---
(emission),
а
дифференциальное
сечение, при
котором
происходит
вынужденное
поглощение
фотонов из
внешней
волны ---

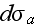 (absorption).
Если
интересоваться
только
увеличением
или
уменьшением
числа
фотонов, то
имеет смысл
ввести
понятие
полное
дифференциальное
сечение
процесса
(absorption).
Если
интересоваться
только
увеличением
или
уменьшением
числа
фотонов, то
имеет смысл
ввести
понятие
полное
дифференциальное
сечение
процесса

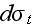 (total):
(total):
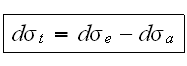
Полное дифференциальное сечение связано с изменением числа фотонов внешней волны, т.е. с ее усилением или ослаблением.
------------
Для
нахождения
дифференциальные
сечения
излучения и
поглощения
запишем
уравнение
Дирака в
поле плоской
волны:
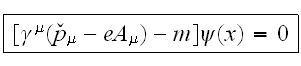
где

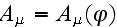 ,
,

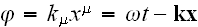 .
.
Решение этого уравнения впервые получено Д.Волковым в 1937 г. и широко стало использоваться в начале 60-хх всвязи с созданием лазера, т. к. решение Влокова моделирует поле лазера. В настоящее время существует целый раздел физики --- лазерная физика, изучающий взаимодействие лазерного излучения с веществом как экспериментально, так и теоретически. Повторим кратко это решение.
Домножим
уравнение
Дирака на

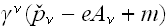 :
:
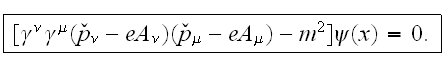
Учтем то, что
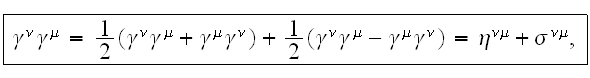
тогда после
преобразований: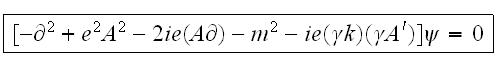
Итак,
уравнение
Дирака
преобразуется
к
дифференциальному
уравнению
второго
порядка.
Отметим, что
это
уравнение
содержит
лишнее
решение.
Решение
будем искать
в
виде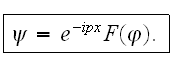
Подставим
это
выражение в
дифференциальное
уравнение и
после
преобразований
получим:
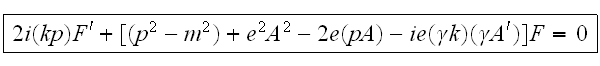
В этом
решении
4-вектор

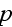 определен
неоднозначно
и на него
можно
наложить
дополнительное
условие,
например
определен
неоднозначно
и на него
можно
наложить
дополнительное
условие,
например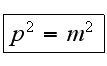
Отсюда
следует, что
при
выключении
внешнего
поля 4-вектор

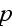 имеет
физический
смысл
4-импульса
свободного
электрона.
имеет
физический
смысл
4-импульса
свободного
электрона.
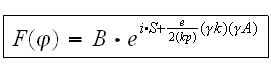
где
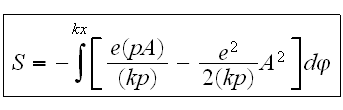
Константу
положим
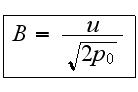
Все степени

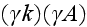 выше первой
равны нулю,
поскольку
выше первой
равны нулю,
поскольку
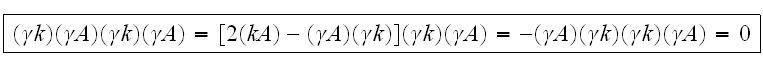
В силу этого
можно
заменить
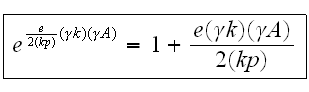
Окончательно
решение
Волкова
имеет вид:
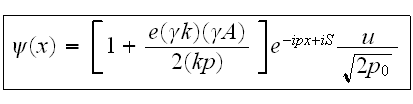
При
выключении
внещнего
поля функция
Волкова
переходит в
решение
уравнения
Дирака для
свободного
электрона.
Отсюда
видно, что

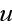 -- биспинор
свободного
электрона и
на него
можно
наложить
условие
нормировки
-- биспинор
свободного
электрона и
на него
можно
наложить
условие
нормировки
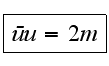
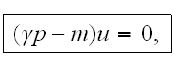
которое и отбрасывает лишнее решение.
Такм образом, у нас есть выражение для Волковской функции, являющейся решением уравнения Дирака в поле плоской электромагнитной волны. Это выражение и позволит нам найти дифференциальные излучения процесоов вынужденного излучения и погложения фотонов.
------------
Рассмотрим
сначала
протекание
процесса в
поле одной
эллиптически
поляризованной
волны, для
которой
4-потенциал
электромагнитного
поля имеет
вид:
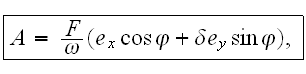
где

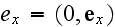 ,
,

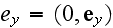 -- 4-векторы
поляризации
волны,
-- 4-векторы
поляризации
волны,

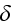 -- параметр
элиптичности
волны,
-- параметр
элиптичности
волны,

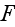 и
и

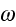 --
напряженность
и частота
волны,
аргумент
--
напряженность
и частота
волны,
аргумент

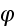 имеет вид
имеет вид

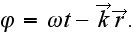
Разлагая
решение
уравнения
Дирака в ряд
Фурье
получим:
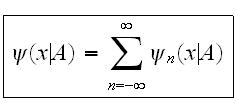
где
парциальные
волновые
функции

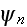 ,
отвечающие
всевозможным
процессам
вынужденного
излучения и
поглощения
электроном
,
отвечающие
всевозможным
процессам
вынужденного
излучения и
поглощения
электроном

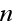 фотонов
волны, имеют
вид:
фотонов
волны, имеют
вид:
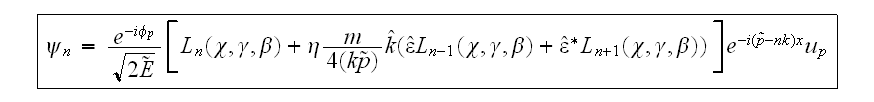
Здесь

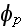 -- фаза, не
зависящая от
индекса
суммирования,
-- фаза, не
зависящая от
индекса
суммирования,

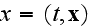 -- 4-вектор,
-- 4-вектор,

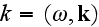 -- 4-импульс
фотона
внешнего
поля,
-- 4-импульс
фотона
внешнего
поля,

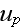 -- биспинор
Дирака,
выражение со
шляпками
обозначают
скалярные
произведения
матриц
Дирака
-- биспинор
Дирака,
выражение со
шляпками
обозначают
скалярные
произведения
матриц
Дирака

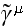 (
(
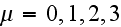 )
с
соответствующими
4-векторами
(
)
с
соответствующими
4-векторами
(
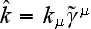 ),
4-вектор
),
4-вектор

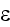 и
4-квазиимпульс
и
4-квазиимпульс

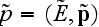 соответственно
равны
соответственно
равны
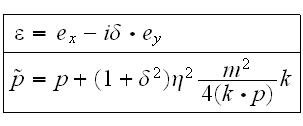
где
релятивистски
инвариантный
параметр

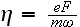 численно
равен
отношению
работы поля
на длине
волны к
энергии
покоя
электрона и
характеризует
интенсивность
волны.
численно
равен
отношению
работы поля
на длине
волны к
энергии
покоя
электрона и
характеризует
интенсивность
волны.
Функция

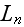 зависит от
трёх
релятивистски
инвариантных
параметров
зависит от
трёх
релятивистски
инвариантных
параметров

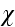 ,
,

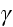 ,
,

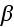 и имеет
следующий
вид::
и имеет
следующий
вид::
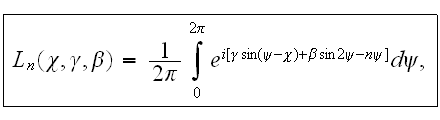
где
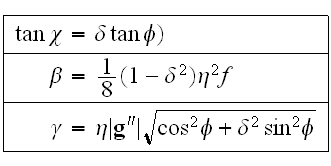
Здесь

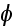 -- угол между
-- угол между

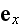 и
параллельной
плоскости
и
параллельной
плоскости

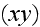 компонентой
компонентой

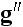 вектора
вектора

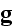 ,
а 4-вектор
,
а 4-вектор

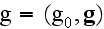 и
релятивистски
инвариантная
функция
и
релятивистски
инвариантная
функция

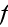 имеют
следующий
вид:
имеют
следующий
вид:
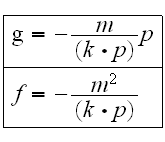
Отметим, что
функции

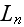 можно
разложить в
ряд по
функциям
Бесселя
целочисленного
порядка
можно
разложить в
ряд по
функциям
Бесселя
целочисленного
порядка

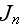
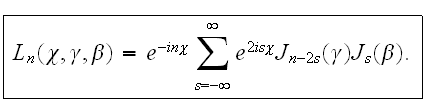
Из
интегрального
представления

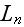 видно,
что эта
функция
является
видно,
что эта
функция
является

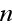 -коэффициентом
фурье для
-коэффициентом
фурье для
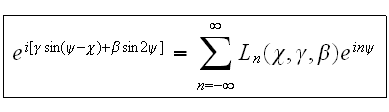
Существенно
подчеркнуть,
что функции

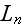 определяют
вероятность
многофотонных
процессов в
поле одной
плоской
электромагнитной
волны.
определяют
вероятность
многофотонных
процессов в
поле одной
плоской
электромагнитной
волны.
------------
Теперь
усложним
задачу и
выберем
4-потенциал
внешнего
электромагнитного
поля в виде
суммы двух
плоских
волн,
распространяющихся
вдоль оси

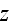 :
:
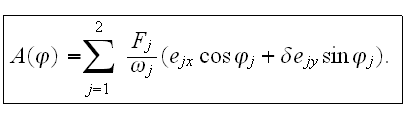
Разлагаем
решение
Волкова в
таком поле в
двойной ряд
Фурье:
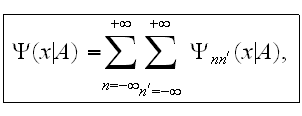
где
парциальные
волновые
функции

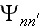 ,
отвечающие
всевозможным
процессам
вынужденного
излучения и
поглощения
электроном
,
отвечающие
всевозможным
процессам
вынужденного
излучения и
поглощения
электроном

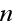 фотонов
первой волны
и
фотонов
первой волны
и

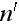 фотонов
второй
волны, имеют
вид:
фотонов
второй
волны, имеют
вид:
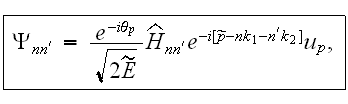
где
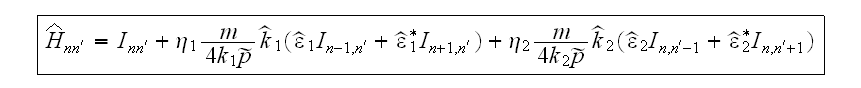
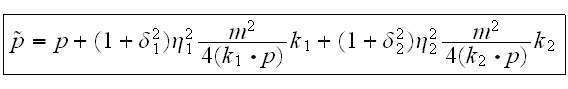
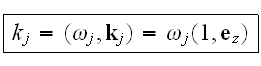
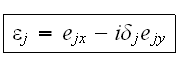
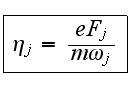
Здесь

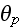 -- фаза, не
зависящая от
индекса
суммирования,
-- фаза, не
зависящая от
индекса
суммирования,

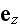 -- единичный
вектор вдоль
направления
движения
обеих волн.
-- единичный
вектор вдоль
направления
движения
обеих волн.
Функция

 зависит от
десяти
релятивистски
инвариантных
параметров:
зависит от
десяти
релятивистски
инвариантных
параметров:
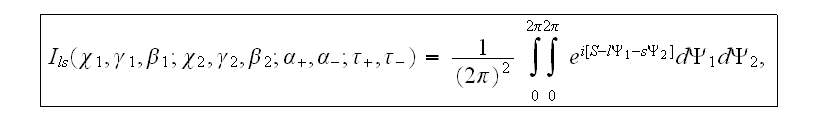
где

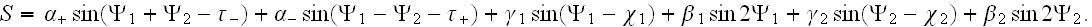
Здесь
параметры
двух волн

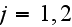 были введены
следующим
образом:
были введены
следующим
образом:
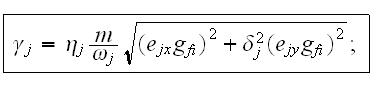
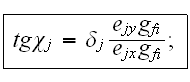
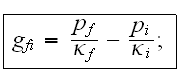
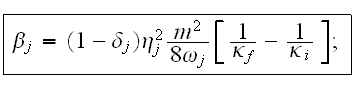
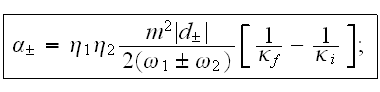
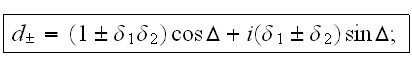
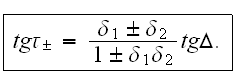
Здесь

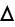 -- угол между
-- угол между

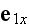 и
и

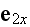 ,
,

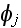 -- угол между
-- угол между

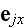 и
параллельной
плоскости
и
параллельной
плоскости

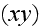 компонентой
компонентой

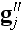 вектора
вектора

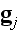 .
4-вектор
.
4-вектор

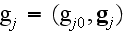 и
релятивистски
инвариантные
функции
и
релятивистски
инвариантные
функции

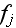 и
и

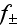 имеют вид
имеют вид
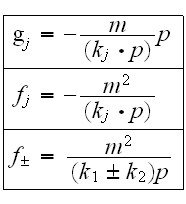
Из
интегрального
представления
видно, что
функции

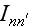 являются
коэффициентами
Фурье
функции
являются
коэффициентами
Фурье
функции
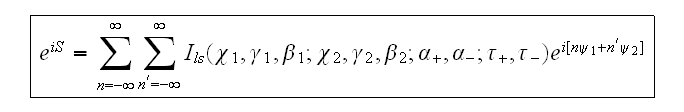
Существенно
подчеркнуть,
что функции

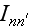 определяют
вероятность
многофотонных
процессов в
поле двух
плоских
электромагнитных
волн.
определяют
вероятность
многофотонных
процессов в
поле двух
плоских
электромагнитных
волн.
-----------
С помощью полученных соотношений мы можем теперь найти дифференциальное сечение вынужденного тормозного излучения при рассеянии электрона на ядре в поле этих двух электромагнитных волн следующим образом:
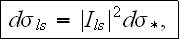
дифференциальное
сечение
Мотта
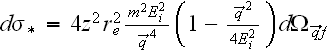 где
обозначено
где
обозначено

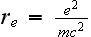 ,
,

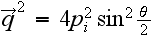 .
.
Т.о. имеем
возможность
для
различных
интенсивностей

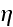 ,
частот
,
частот

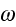 и
поляризаций
и
поляризаций

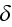 волн
численно
найти полное
дифференциальное
сечение,
нормированное
на сечение
Мотта.
волн
численно
найти полное
дифференциальное
сечение,
нормированное
на сечение
Мотта.
Возвращаемся
к нахождению
полных
дифференциальных
сечений
излучения и
поглощения:
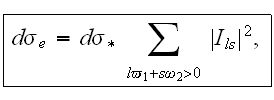
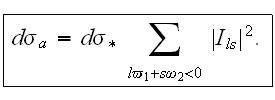
Исследовалось
среднее по
углам влёта
электрона
сечение:
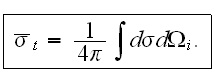
Отдельно
исследовались
так
называемые
интерференционная
и
неинтерференционная
области.
Интерференционной
считается
область, в
которой
рассеяние
происходит в
плоскости,
образованной
импульсом
начального
электрона и
волновым
вектором,
причём
азимутальные
углы
направлений
движения
электрона в
начальном и
конечном
состояниях
равны, а
полярные
связаны
соотношением:
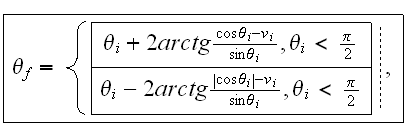
где

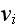 - начальная
скорость
электрона.
- начальная
скорость
электрона.
Результаты вычислений покажем в виде следующих основных графиков:
1)
зависимость
среднего
полного
дифференциального
сечения

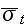 от начальной
скорости
электрона в
неинтерференционной
области:
от начальной
скорости
электрона в
неинтерференционной
области:

2)
зависимость
среднего
полного
дифференциального
сечения

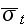 от начальной
скорости
электрона в
интерференционной
области:
от начальной
скорости
электрона в
интерференционной
области:

Видим, что как в интерференционной, так и в неинтерференционной областях поглощение в основном преобладает над излучением, т.е. излучение ослабляется, однако существуют определённые области начальных скоростей электрона, в которых излучение преобладает над поглощением, т.е. имеет место усиление света. Сравнение абсолютных величин полного сечения в неинтерференционной и интерференционной областях показывает, что усиление электромагнитных волн в основном имеет место в интерференционной области и вероятность этого почти в 3 раза превышает соответствующую вероятность в неинтерференционной области.
Таким образом, наша цель достигнута - мы показали, что при определённых условиях лазерные лучи, проходящие через вещество, могут усиливаться! Это совершенно новый результат, открывающий новое направление исследований в физике взаимодействия интенсивного электромагнитного излучения с вешеством и новые горизонты применения рассмотреных эффектов в технике.
References
1. Волков Д. М. Электрон в поле плоских неполяризованных электромагнитных волн с точки зрения уравнения Дирака, 1937, ЖЕТФ т.7, с.1286.
2. Kotseroglou T., Bamber C., Boege S. et. al. PICOSECOND TIMING of TERAWATT LASER PULSES with the SLAC 46 GEV ELECTRON BEAM. SLAC-PUB 7130. 1996. Princeton Rochester, SLAC, Tennessee collaboration.
3. Делоне Н.Б. Взаимодействие лазерного излучения с веществом. Москва.: Наука, 1989.
4. Рапопорт Л.П., Зон Б.А., Манаков Н.Л. Теория многофотонных процессов в атомах. Москва.: Атомиздат, 1978.
5. Лебедев И.В., 1970, Оптика и спектроскопия 19, с.948.
6. Делоне Н.Б., Крайнов В.П. Атом в сильном световом поле . Москва.: Энергоиздат, 1984.
7. Делоне Н.Б., Крайнов В.П. Многофотонная ионизация атомов: новые эффекты.// УФН, 1989. Т.158. Вып. 2. С. 215-253.
8. Фёдоров М.В. Электрон в сильном световом поле. Москва.: Наука, 1991.
9. Иванов Г.К., Голубков Г.В. 1991, ЖЕТФ т.99, с.1404.
10. Никишов А.И., Ритус В.И. Квантовая электродинамика явлений в интенсивном поле. Труды ФИАН. Т. 111. Москва.: Наука, 1979. (Никишов А. И., Ритус В. И., 1979, Труды ФИАН, 111.)
11. Олейник В.П., Белоусов И.В., 1983, Проблемы квантовой электродинамики вакуума, диспергирующих сред и сильных полей. Кишинев.
12. Лебедев И.В. Генерация гармоник при торможении электрона в присутствии интенсивной световой волны, 1972, Оптика и спектроскопия т.32, с.120.
13. Борисов А.В., Жуковский В.Ч. Тормозное излучение электрона на ядре в поле плоской электромагнитной волны, 1976, ЖЭТФ т.70, с.477.
14. Карапетян Р.В., Федоров М.В. Спонтанное тормозное излучение электрона в поле интенсивной электромагнитной волны, 1978, ЖЭТФ т.75, с.816.
15. Борисов А.В., Жуковский В.Ч., Эминов П.А. Резонансное тормозное излучение электрона на электроне в поле электромагнитной волны, 1980, ЖЭТФ 78, с.530.
16. Крайнов В.П., Рощупкин С.П. Тормозное излучение медленного электрона на кулоновском центре во внешнем электромагнитном поле, 1983, ЖЭТФ т.84, с.1302.
17. Рощупкин С.П. Спонтанный тормозной эффект при рассеянии электронов в поле плоской электромагнитной волны, 1983, Известия вузов, Физика вып.4, с.18.
18. Рощупкин С.П. Тормозное излучение релятивистского электрона на ядре в сильном электромагнитном поле, 1985, Ядерная физика т.41, с.1244.
19. Карапетян Р.В., Федоров М.В. Влияние интенсивной электромагнитной волны на процесс вынужденного тормозного излучения электронов, 1977, Квантовая электроника т.4, с.2203.
20. Gorodinskii R.L. and Roshchupkin S.P. Induced Bremsstrahlung Process for a Relativistic Electron Colliding with a Nucleus in a Field of Two Electromagnetic Waves of Arbitrary Intensities and Frequencies, 1992, Laser Physics 2, с.602.
21. Рощупкин С.П., 1994, ЖЭТФ 106, с.102.
22. Рощупкин С.П., 1996, ЖЭТФ 109, с.337.
23. Roshchupkin S.P. and Voroshilo A.I., 1997, Laser Physics 7, с.873.
24. Рощупкин С.П., Лысенко О.Б. Спонтанный интерференционный тормозной эффект при рассеянии релятивистского электрона на ядре в поле двух световых волн, 1999, ЖЭТФ 116, с.1210.
25. Roshchupkin S.P., Tsibulnik V.A., Chmiryov A.N. The Probability of Multiphoton Processes in Quantum-Electrodynamic Phenomena in a Strong Light Field, 2000, Laser Physics 10, p.1256.
26. Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П., 1980, Квантовая электродинамика, Наука, Москва.
27. Scwinger J. On Gauge Invariance and Vacuum Polarization, 1951, Phys. Rev. 82, p.664.
28. Brown L.S., Kibble T.W.B. Interactin of Intense Laser Beams With Electrons, 1964, Phys. Rev. 133, A705.
29. Никишов А. И., Ритус В. И., 1964, ЖЭТФ 47, 1130.
30. Бункин Ф.В., Федоров М.В., 1965, ЖЭТФ 49, 1215.
31. Reiss H.R., Eberly J.H., 1966, Phys. Rev. 151, 1058.
32. Яковлев В.П., 1966, ЖЭТФ 51, 617.
33. Никишов А.И., Ритус В.И., 1967, ЖЭТФ 52, 1707.
34. Денисов М.М., Федоров М.В., 1967, ЖЭТФ 53, 1340.
35. Олейник В.П. 1967, ЖЭТФ 52, 1049.
36. Олейник В.П. 1967, ЖЭТФ 53, 1997.
37. Тернов И.М., Багров В.Г., Клименко Ю.И., 1968, Известия вузов, Физика 2, 50.
38. Бункин Ф.В., Казаков А.Е., Федоров М.В., 1972, УФН 107, 559.
39. Bos J., Brock W., Mitter H., Schott Th., 1979, J. Phys. A12, 715.
40. Bos J., Brock W., Mitter H., Schott Th., 1979, J. Phys. A12, 2573.
41. Reiss H.H., 1980, Phys. Rev. A 22, 1786.
42. Bergou J., Varro S., Fedorov M.V., 1981, J. Phys. A14, 2305.
43. Клименко Ю.И., Кулиш В.В., Худомьясов А.И., 1974, Известия вузов, Физика 2, 50.
44. Клименко Ю.И., Кулиш В.В., Федосов И.И., Худомьясов А.И., 1976, Известия вузов, Физика 4, 136.
45. Радионов В.И., 1981, ЖЭТФ 81, 187.
46. Рощупкин С.П., 1983, Известия вузов, Физика 4, 18.
47. Рощупкин С.П., 1983, Известия вузов, Физика 8, 12.
48. Рощупкин С.П., 1984, Оптика и спектроскопия 56, 36.
49. Fedorov M.V., Roshchupkin S.P. , 1984, J. Phys.A: Math. Gen.17, 3143.
50. Лысенко А.В., Рощупкин С.П., 1991, Украинский физический журнал 36, 7.
51. Рощупкин С.П., 1991, Украинский физический журнал 36, 967.
52. Roshchupkin S.P., 1993, Laser Physics 3, 414.
53. Denisenko O.I., Roshchupkin S.P., 1993, Laser Physics 3, 903.
54. Roshchupkin S.P., 1994, Laser Physics 4, 139.
55. Denisenko O.I and Roshchupkin S.P., 1994, Physika Scripta 50, 339.
56. Roshchupkin S.P., 1996, Laser Physics 6, 837.
57. Voroshilo A.I. and Roshchupkin S.P., 1997, Laser Physics 7, 466.
58. Рощупкин С.П., Ворошило А.И., 1997, Вiсник Сумського держунiверситету 1(7), 126.
59. Рощупкин С.П., Лысенко О.Б., 1998, Вiсник Сумського держунiверситету 1(9), 24.
60. Ворошило А.I., Рощупкiн С.П., 1999, Украiнський фiзичний журнал 44, 446.
61. Roshchupkin S.P. and Lysenko O.B., 1999, Laser Physics 9, 494.
62. Denisenko O.I. and Roshchupkin S.P., 1999, Laser Physics 9, 1108.