
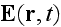 is applied to a material, the response of the material through the
polarization
is applied to a material, the response of the material through the
polarization

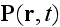 (i.e. the induced dipole moment per unit volume) described as
(i.e. the induced dipole moment per unit volume) described as
This is the fascinating physical field for the multiscale description, modeling and design of new solid state devices. We have been only making the first steps toward the theory of VA optics multiscale nonlinear formulations and mathematics. There are some first theoretical texts and solutions we had been produced anyway.
Meanwhile, some interesting facts, the theoretical (based on the published one scale solutions) as well as experimental findings have been already put into the NRIM (Negative Refractive Index Materials) subsection, please, look below. Those experimental facts are many more, albeit the explanations sought in the one scale arena. Still, the NRIM is such a straight experimental prove of the two-scaled composites optical behavior.
Also, in the Laser Optics subsection people would find some techniques researchers are using right now, and this can be the very nice multiatomic problems formulation for the Laser Optics when the scaling HSP-VAT methods, tools will be used. People in Laser Optics don't know (well, they used to think that they operate the proper techniques of averaging, nonlocality mathematics, but those are not correct ones) how to approach the collective behavior problems. This problem lasts since the first half of XXth century when all particles, especially photons, were accepted as the point-mass objects (what is the volumeless object with a mass? who knows?) and when the mathematics was of a one scale. There have been published firstly in this website the Russian and the English texts of a good piece of work as the preliminary study for the two-scale description.
In Nonlinear Optics there is already exists the nonlocal description models when raising from the nanoscale (even atomic scale) description to the larger scale. The one which consists of the main set of governing equations which is the base of "pseudo-nonlocal" description, for example of polarization field. That is being modeled mostly (and here, only as an example) as the lump sum mechanism - which is not, as readers know.
When an electromagnetic field

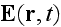 is applied to a material, the response of the material through the
polarization
is applied to a material, the response of the material through the
polarization

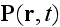 (i.e. the induced dipole moment per unit volume) described as
(i.e. the induced dipole moment per unit volume) described as
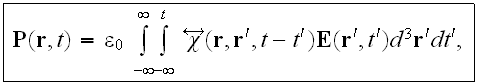
where

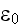 is the vacuum permittivity and
is the vacuum permittivity and

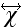 is the susceptibility tensor of the material.
is the susceptibility tensor of the material.
Often the local response approximations applied (i.e. the
response

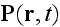 is considered to depend only on the field
is considered to depend only on the field

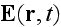 at the space coordinate
at the space coordinate

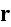 ).
In this case we can write
).
In this case we can write
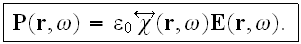
If the material is nonlinear then the usual method to apply is that the susceptibility

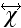 can be expanded in powers of the electric field and the polarization field can
be written
can be expanded in powers of the electric field and the polarization field can
be written
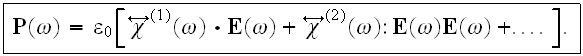
and then used in the Maxwell's equations and numerous coupled modes can be formulated and studied.
The response of a material (the polarization) then used in the Maxwell's equations and numerous coupled modes can be formulated and studied. In case of second order nonlinearities three waves are mixed by the coupled nonlinear wave equations. This so-called three wave mixing is responsible for the usual second order effects like the second harmonic generation, etc. The basic equations starting with are Maxwell's equations for non-magnetic materials
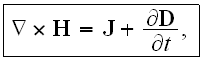
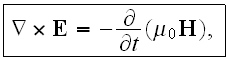
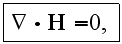
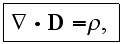
and the material equations
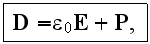
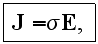
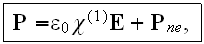
where

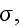 the specific conductivity, and where
the specific conductivity, and where

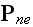 is the nonlinear part of the polarization field.
Following Yariv (1975) and Yariv and Yeh (1984) the polarization is often
written in the following form
is the nonlinear part of the polarization field.
Following Yariv (1975) and Yariv and Yeh (1984) the polarization is often
written in the following form
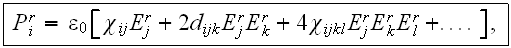
using only the term for nonlinear polarization input as
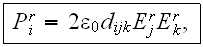
where

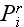 and
and

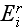 are the i-th components of the field, and where summation over repeated
indices is assumed. The superscript
are the i-th components of the field, and where summation over repeated
indices is assumed. The superscript

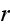 indicates that these fields are real fields that can be expressed in terms of
their complex amplitudes
indicates that these fields are real fields that can be expressed in terms of
their complex amplitudes
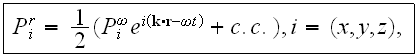
where c.c. means the complex conjugate.
Consider the two fields at frequencies

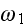 and
and

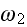
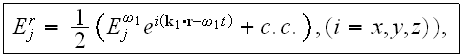
and
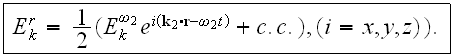
Taking only the frequency

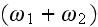 terms the polarization becomes
terms the polarization becomes
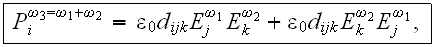
where it is assumed that
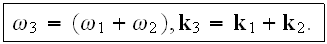
For case of second harmonic generation where

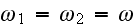 the field components
the field components

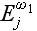 and
and

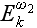 are the components of the same field, then
are the components of the same field, then
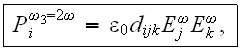
with summation over repeated indices. Anyway, the second order effect is given by
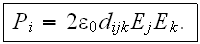
Then the usual wave equation for the electric field can be seen as
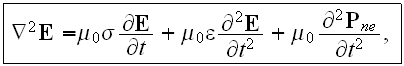
where
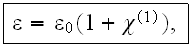
is the linear part of the dielectric constant of the material.
Introducing the complex amplitudes and considering for simplicity a scalar
approximation the real field amplitude is given
by

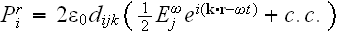
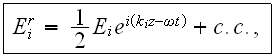
then, after multiple assumptions the wave equation can be written as (Skettrup, 1990)
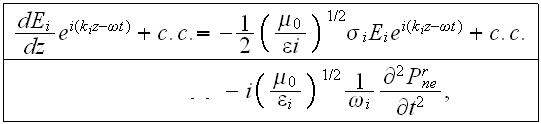
where
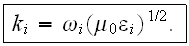
We see here that with this interpretation of the nonlinear Maxwell's equations
- the

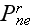 - term acts as a source term in the electric field.
- term acts as a source term in the electric field.
The obvious cause of the generation via the Second Harmonic involvement appears to be the natural mechanisms delivering models for composite, irregular, simply ordinary media with defects, including also interfaces. "The second harmonic (SH) signal is generated because of the discontinuities occurring at the surface"... - Coutaz (1990).
For the metal with plane surface the incident strong EM field causes the expression for the NL polarization inside the metal close to its surface (Coutaz, (1990)

where

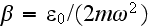 and
and

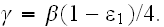
Other numerous features, for example, like regarding the modes in Optical Fibers which have the self-prepared SHG - "since in theory all such second-order nonlinear optical processes are disallowed" (Weinberger, 1990; p. 162) are interesting for study in terms of the Heterogeneous Polarization and the interscale communication.
some CONCLUSIONSWe have here noticed only a few features among the non-linear Optics phenomena described with mixing of scales. We will be adding from time to time interesting developments or/and comments related to multiscale phenomena description in HSP-VAT Heterogeneous Hierarchical/Scaled Optics, as we have done so in some below subsections.
References:
Flytzanis, C., Hache, F., Klein, M.C., Ricard, D., and Roussignol, Ph., (1991), "Nonlinear Optics in Composite Materials. 1. Semiconductors and Metal Crystallites in Dielectrics," Chap. V in Progress in Optics, Vol. XXIX, E.Wolf, ed., Elsevier Science Publ., Amsterdam, pp. 321-411.
Frisch, U., Wave Propagation in Random Media. II. Multiple Scattering by n Bodies, Institut d'Astrophysique, Paris, 1965.
Harper, P.G. and Wherret, B.S., (Eds.), Nonlinear Optics, Academic Press, London, 1977.
Keller, O., ed., Nonlinear Optics in Solids, Springer-Verlag, Berlin, 1990.
Rytov, S.M., Kravtsov, Yu.A., and Tatarskii, V.I., Principles of Statistical Radiophysics, Vol. 3, Random Fields, Springer, Berlin, Heidelberg, 1989.
Rytov, S.M., Kravtsov, Yu.A., and Tatarskii, V.I., Principles of Statistical Radiophysics, Vol. 4, Wave Propagation Through Random Media, Springer, Berlin, Heidelberg, 1989.
Shen, Y.R., The principles of Nonlinear Optics, John Wiley & Sons, New York, 1984.
Skettrup, T., "Second Order Nonlinear Optical Effects," in Nonlinear Optics in Solids, Springer-Verlag, Berlin, pp. 8-23, 1990.
Soukoulis, C.M., ed., (1993), Photonic Band Gaps and Localization, Plenum, New York.
Soukoulis, C.M., ed., (1996), Photonic Band Gap Materials, Kluwer Academic Publishers, Dordrecht. 729 p.
Weinberger, D.-A., "Second Harmonic Generation in optical Fibers," in Nonlinear Optics in Solids, Springer-Verlag, Berlin, pp. 162-184, 1990.
Ufimtsev, P.Ya., The Method of Edge Waves in the Physical Theory of Diffraction, US Air Forse, Wright-Patterson AFB, OH, 1971.
Yariv, A., Quantum Electronics, John Wiley & Sons, New York, 1975.
Yariv, A. and Yeh, P., Optical Waves in Crystals, John Wiley & Sons, New York, 1984.
