We would like to say some notes regarding the definitions of these concepts, those taken as being granted. When the problem, the physics of the problem demanding and has the features of different scale physics, then we need to do something about it. The easiest way is just to ignore this and say for a particular problem - that "these are the respected scale features." As it is done with, for example, the Molecular Dynamics (MD) simulations. After simulation of the huge amount of atoms or molecules in the box, then the whole box properties are declared as the specified material's properties. The trick is that in MD also used the numerous atomic scale physics approximations and assumptions, and still the results can be driven to a reasonable proximity to experiment, or vice versa. After all, the experiment is also the single scale homogeneous one.
The reason to distinguish the point defined local and the non-local field's values at the same coordinate system is following the same famous theorems we are discussing here in this website - the Ostrogradsky-Gauss (OG) (or Gauss-Ostrogradsky - GO) theorem or the Heterogeneous Whitaker-Slattery-Anderson-Marle (WSAM) kinds of theorem. The reason why in some languages - in Russian particular, is taken lead to Ostrogradsky in the naming of this theorem, is that because Gauss actually did not formally discover and did not prove this theorem. He used the mathematical formulation of it, he was sure, intuitively perhaps, that the mathematical statement is correct. The OG theorem was proven and studied in the early 19-th century by famous Russian mathematician Ostrogradsky.
Note, this is not only the professional scientific website - but the educational as well, therefore some notes from the history are available.
So, we know that each and every mathematical physics governing equation started from the use of the OG theorem. That means, we already included implicitly in the development of these equations the definitions of the two spaces and the two coordinate systems at each of the spaces agreed for consideration ! Right ?
The lower scale (actually the same scale, but non-local) physics variables and properties then silently declared as irrelevant, unimportant - hereby we do not use, mention and mean that the point in our mathematical homogeneous formulation is actually the volume used in the OG theorem to obtain the current equation of interest. This approach is justified as soon as the matter assumed as of a homogeneous nature, because there are the mathematical theorems showing that the limit transitions when the size of a spatial domain collapses to an infinitely small one are presenting the properties of this domain in the selected internal point into which it collapses.
There are also the non-local homogeneous media properties. Those also use the basis of integration, or averaging. Integration is taken as for the continuous functions.
This legitimate base allows us to approach the variety of media, materials, but only the Homogeneous ones. For Heterogeneous media and materials there are the WSAM kind of theorems exist. And the reason for the definitions of at least two scale spaces and physics became the pivotal one.
This, in turn brings the problem of definitions for the point-like Lower and the point-like Upper scale physical fields. Consecutively, we need to define the non-local, averaged fields for stated Heterogeneous problems at their corresponding scales.
We should obey to this original set up done two centuries ago in Physics and in Mathematics for the homogeneous media and translate it onto the heterogeneous, scaled media.
The great issue in all of this is the connection, communication between the physics and properties of each of the two spaces.
While for the homogeneous medium this question is never surfaces and discus's, for Heterogeneous media we need to specify these definitions with the greater detail.
After all, this is in the heart of scaling heterogeneous physics as it must work.
Thus, we start with the definition of a point, a dot used in the mathematical formulation of physical problems (not a strict one, which definition we leave for a more appropriate situation with the mathematics discussed).
- At the known and assigned previously system of coordinate the point is the object with no dimension in any of the three coordinates, and this object has the descriptive features, which determine the location of that point in the assigned system of coordinates. The point located physical property has this spatial point determined value.
DEFINITION
Following the OG theorem we now know that - if at any point with the coordinates inside of the problem's domain is known the functional dependency for a physical field, which in the most of physical sciences right now is the partial differential or just differential equation(s), then we imply that the domain which served for the derivation of this equation via the OG theorem was the domain of the Lower subspace - because in that theorem we start doing an integration over the finite volume and the finite surface(s).
Now - why not apply the same concept to the heterogeneous media, which means - that after the averaging provided according to the one of the WSAM theorems - we get the mathematical equation (dependency) of the higher (another) space. With the corresponding spatial dependencies and the topology of the physical spatial fields.
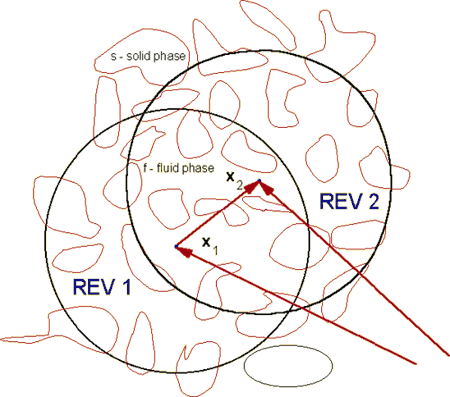
With the one substantial different feature - we can not infinitely reduce the size, the volume of this domain -
because we want to keep the most of descriptive features of the both (or more) phases inside of our spatial domain.
- The Upper Space point when connected to the Lower Scale Domain REV (Representative Elementary Volume) might reflect, determine, and establish the features of communications between the both space physics. These features can be of different physical description in accordance to their respected space physics definitions. And vise versa - the Higher Space point physics might control, govern, reflect, and determine in some ways the properties of the Lower Scale physical Domain.
DEFINITION 2
-
It is easier to discuss and argue in favor of these definitions right now - after the number of problems were solved in the said mode - when the Lower and Upper scale HSP-VAT governing equations were connected Directly before and during their respected solutions.
The brightest example for viewing the situation as the said above is the transition from the atomic (atomistic if you want that) spatial scale dependencies - dependencies described by atomic physics discipline, to the continuum physics laws and dependencies.
Most of the people do not see this as a problem while doing a description? But it is, the situation probably took everybody interested in it to become so tired that this is just agreed to accept - that from the atomic physics the jump to the continuum description would be as we just become agreed!? That's it !
Most of the people do not know what kind of heated discussions went on this issue at the turn of the 20-th century.
Making an example from the Lorentz theory of dielectric materials - we go from the atomic scale description just onto the continuum scale description - and in the Conventional Orthodox Homogeneous Physics (COHP) mode.
We will see that there is no real mathematics of spatial averaging was attached to this theory as is. That was and is an example of what is taught to students in the universities as for the spatial "averaging" as granted.
Let we pass through and discuss some of the major rules of this theory.
The Lorentz model was meant for linear dispersive media describing
the dielectric-type media as a collection of neutral atoms with electrons bound to
the nucleus as like with the "elastic forces" (called as a collection
of Lorentz
oscillators). When the electromagnetic field applied into the vicinity of this
atom, the equation of motion of this bound

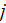 -type
electron is given as
-type
electron is given as
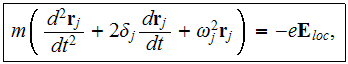
where

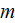 is the mass of this electron and
is the mass of this electron and

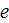 is the value of the electronic charge,
is the value of the electronic charge,

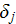 is the phenomenological damping constant for this oscillator,
is the phenomenological damping constant for this oscillator,

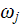 is the undamped resonance frequency of the oscillator. The applied field
is the undamped resonance frequency of the oscillator. The applied field

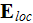 is the LOCAL microscopic electric field.
is the LOCAL microscopic electric field.
Having this field as the monochromatic one with the fixed regular frequency

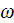 or
or

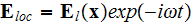 one would get the solution for the equation of motion in the form
one would get the solution for the equation of motion in the form
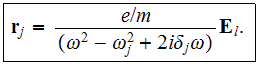
The Local dipole moment induced by this electron becomes
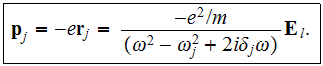
For the each array of these

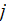 -type
oscillators in a unit volume the Macroscopic polarization
-type
oscillators in a unit volume the Macroscopic polarization

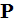 of the dielectric medium considered after using the SUMMATION
(as the spatial Averaging method) over the all
types of electrons present in this unit volume using the number density
of the dielectric medium considered after using the SUMMATION
(as the spatial Averaging method) over the all
types of electrons present in this unit volume using the number density

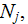 or
or
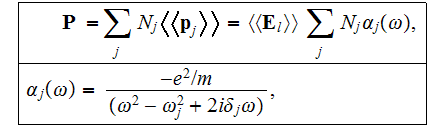
where the double angle brackets

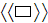 mean a Spatial Average over the considered number of Atomic Sites !
mean a Spatial Average over the considered number of Atomic Sites !
It is not the spatial integration-averaged variable. The value of Atomic
Polarizability of the Lorentz oscillator for each electron

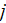 -type
is the
-type
is the

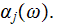 The overall number of arrays of
The overall number of arrays of

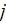 -types
electrons is
-types
electrons is
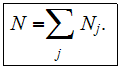
Another important formula connects the same value of the Macroscopic
polarization

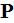 to the susceptibility
to the susceptibility

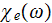 and to the variable of Macroscopic electric field
and to the variable of Macroscopic electric field

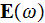 via
via
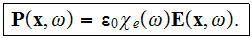
It is strange, but in reality is the accepted thing when the following equality says
that the really averaged value of Macroscopic electric field

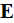 and the atomic sites averaged
and the atomic sites averaged

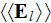 are usually being taken as
are usually being taken as
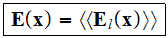
so, just proclaimed as being averaged.
Students - notice, that up to our times - hundred years later, no
real averaging of electron arrays COHP cannot provide neither
in a real good mathematics nor in imaginable conjectures.
Then
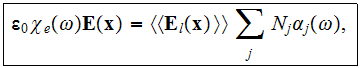
or
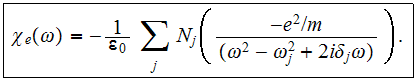
In this way of doing Macroscopic variables

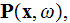

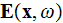 (those are averaged by nature and by experimental techniques) and the sites
"Averaged" variable
(those are averaged by nature and by experimental techniques) and the sites
"Averaged" variable

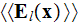 one should draw the conclusion that the variable of susceptibility
one should draw the conclusion that the variable of susceptibility

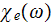 is the "effective" coefficient. And the method of assessment of this
coefficient is also to some extend the frivolous one (obsolete, that was good
for the turn of 20th century, not now) whatever one may say.
is the "effective" coefficient. And the method of assessment of this
coefficient is also to some extend the frivolous one (obsolete, that was good
for the turn of 20th century, not now) whatever one may say.
All of the above makes communication to the important arguments brought forward by Jeffries (1992, 1994) regarding the issue -
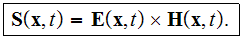
After all, we need to understand that the shrinkage of the Finite Volume during the derivation of the Poynting theorem is ONLY Imaginably can go to the point, collapses to the point. And those definitions of the Macroscopic, "Averaged" fields are incorrect, strictly speaking.
Remember - the point is the subject without the length and volume, meanwhile inside the volume for derivation of the Poynting theorem - we have the much larger objects as atoms, molecules and sub-atomic particles - those are countless number with still their dimensions ! What to do to have all of that being accounted ?
We are doing this in our sections on Heterogeneous Maxwell-Heaviside-Lorentz Electrodynamics as well as for the Galilean electrodynamics well outlined by Ja.G.Klyushin using the scaled communications and the Force-to-Field (FTF) equation.
Jeffries, C., "A New Conservation Law for Classical Electrodynamics," SIAM Review, Vol. 34, No. 4, pp. 386-405 (1992).
Jeffries, C., "Response to Commentary by F.N.H. Robinson," SIAM Review, Vol. 36, No. 4, pp. 638-641 (1994).
Robinson, F.N.H., "Poynting's Vector: Comments on a Recent Paper by Clark Jeffries," SIAM Review, Vol. 36, No. 4, pp. 633-637 (1994).