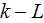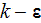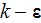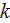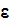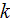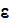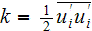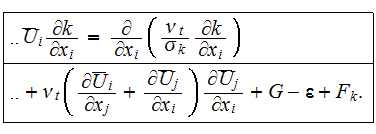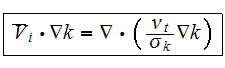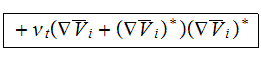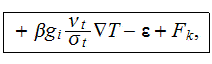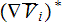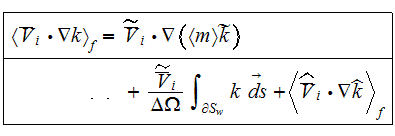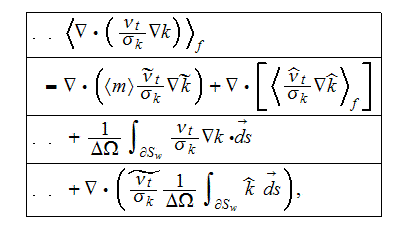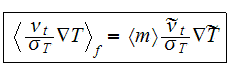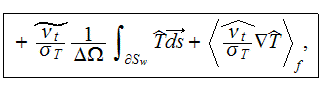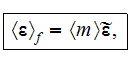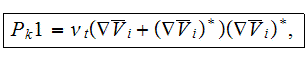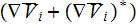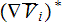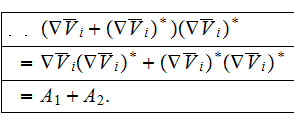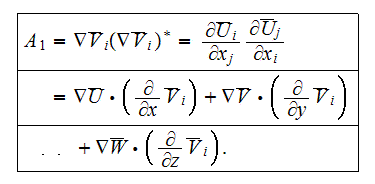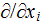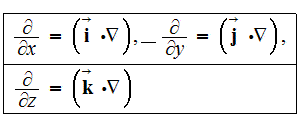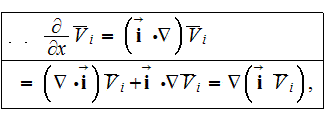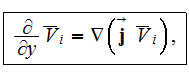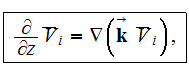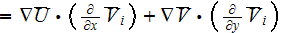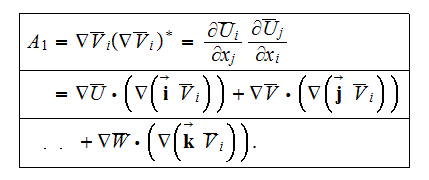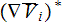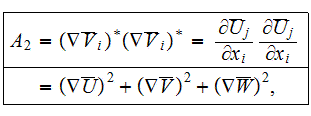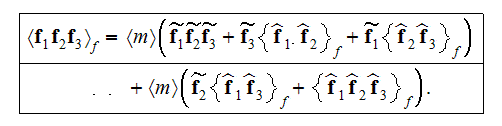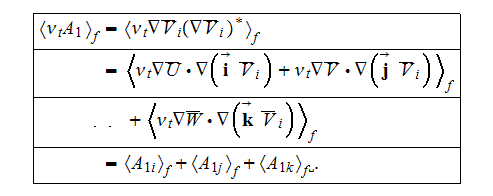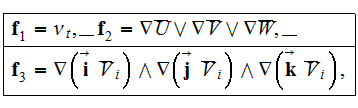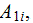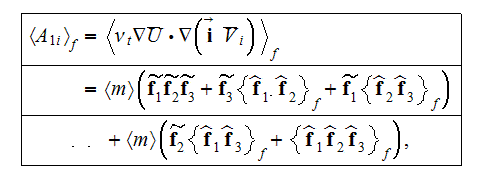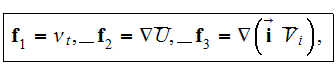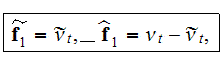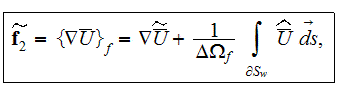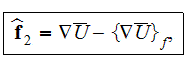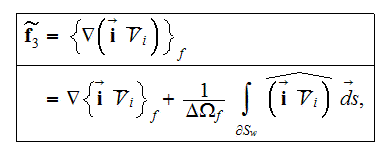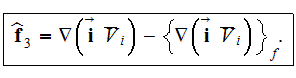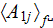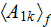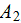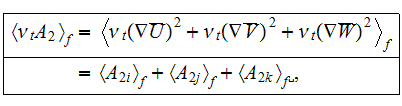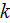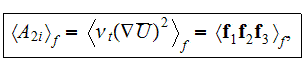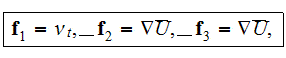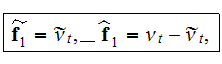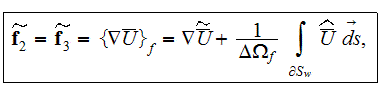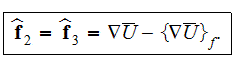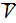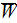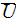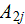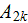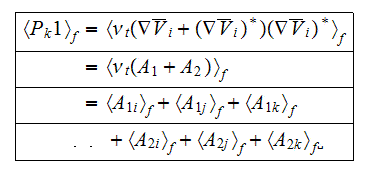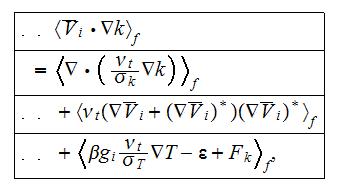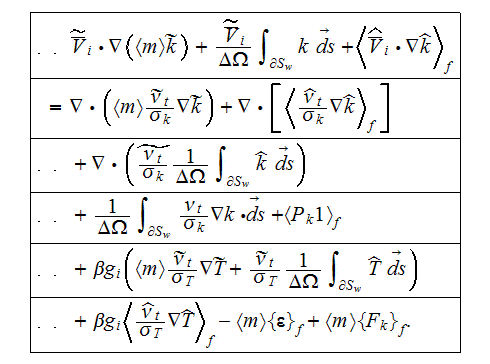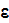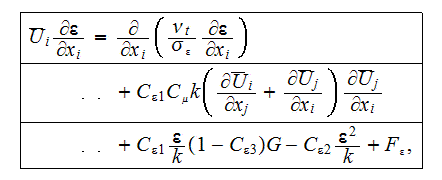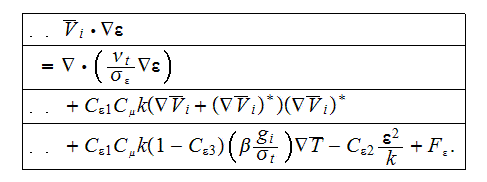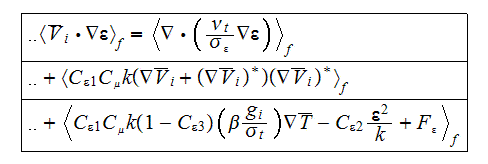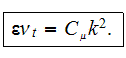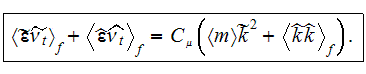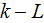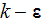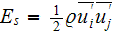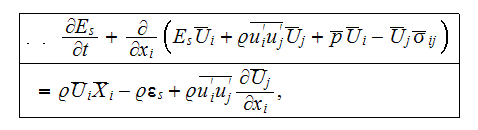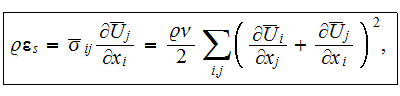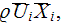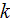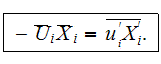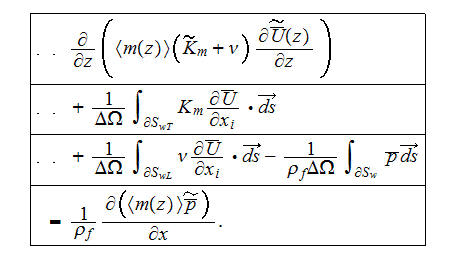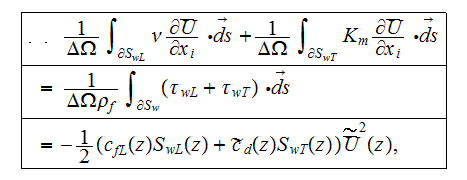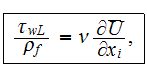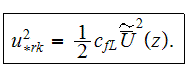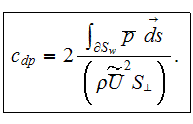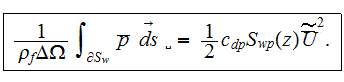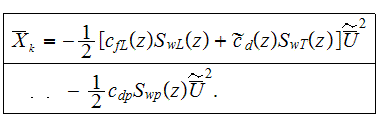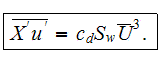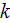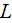The whole field of treating the lower scale turbulent closure equations when the Upper scale VAT averaged fields are
sought is made of the issues of averaging the additional expressions and closure equations
used to be in turbulent science to support a variety of homogeneous fluid turbulent flow theories.
One of them is - "To Average or Not to Average? And What are the consequences?"
And how to do "if to make" the averaging of those highly nonlinear equations? We mentioned in few places of this website, that the very critical, important
methodology of nonlinear terms VAT averaging is the complicated one.
Here is the text with the paper presented at the 3rd ASME/JSME Fluids Engineering Conference,
San Francisco - Travkin, V. S., Hu, K., and Catton, I. (1999). Turbulent kinetic energy and
dissipation rate equation models for momentum transport in porous media. In
Proc. 3rd ASME/JSME Fluids Engineering Conf. - FEDSM99-7275.
Due to restriction on the size of presented for the
3-rd ASME/JSME(1999) conference papers
this text was presented only using the 6 printed pages.
It is really short, and I can'not extend it here with the all supportive, research and technical questions described.
This paper should be viewed as the consistent study to seek the
upper (second) scale kinetic energy and dissipation rate equations averaged mathematical formulations,
those are
the result of strict application of the theorems developed in VAT for linear and non-linear
mathematical expressions.
And at the same time, this paper is of no means suggesting that I am in a favor of using these
exactly forms of said above equations. I have some work and studies, also used the simplified
forms of these equations, and can here to make some sort of ascertaining that this problem is
standing alone and up for future investigations.
Turbulent
Kinetic Energy and Dissipation Rate Equation Models for Momentum Transport in
Porous Media
V. S. Travkin, K. Hu and I. Catton
Department of Mechanical & Aerospace
Engineering
University of California, Los Angeles, CA 90095
Abstract
Among the many possible models for turbulent momentum in porous media, the
so-called
k-
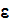 turbulence models are considered to be appropriate for the lowest level of
hierarchical modeling. The fluctuations produced by the porous medium
heterogeneity and wall roughness contribute to the overall transport processes
and to the governing scalar fluctuation equations, the Reynolds stress
equation, the turbulent kinetic energy (TKE) and the dissipation rate of TKE.
These equations must be treated along with other phenomenological
dependencies. In view of the theoretical importance to turbulent transport in
porous media, incompressible turbulent flow within porous media is modeled
using the proper averaging of the transport equations for the turbulent
kinetic energy
(
turbulence models are considered to be appropriate for the lowest level of
hierarchical modeling. The fluctuations produced by the porous medium
heterogeneity and wall roughness contribute to the overall transport processes
and to the governing scalar fluctuation equations, the Reynolds stress
equation, the turbulent kinetic energy (TKE) and the dissipation rate of TKE.
These equations must be treated along with other phenomenological
dependencies. In view of the theoretical importance to turbulent transport in
porous media, incompressible turbulent flow within porous media is modeled
using the proper averaging of the transport equations for the turbulent
kinetic energy
(
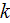 )
and its dissipation rate
(
)
and its dissipation rate
(
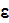 ).The
closures of these model equations are obtained for a few morphologies. The
averaging of these equations is based on strict principles developed for
application of volume averaging theory (VAT). A variety of closure
alternatives are considered for application to the VAT turbulent kinetic
energy and VAT dissipation rate of TKE resulting in a set of simulation
equations. An analysis of other equations used in heterogeneous transport
theories is given for comparison.
).The
closures of these model equations are obtained for a few morphologies. The
averaging of these equations is based on strict principles developed for
application of volume averaging theory (VAT). A variety of closure
alternatives are considered for application to the VAT turbulent kinetic
energy and VAT dissipation rate of TKE resulting in a set of simulation
equations. An analysis of other equations used in heterogeneous transport
theories is given for comparison.
Nomenclature
  |
- |
mean skin friction coefficient over the turbulent area of
  [-]
[-] |
  |
- |
mean drag resistance coefficient in the REV [-] |
  |
- |
mean form resistance coefficient in the REV [-] |
  |
- |
mean skin friction coefficient over the laminar region inside of the REV
[-] |
  |
- |
dimensionless coefficients |
  |
- |
interface differential area in the REV
[  ] ] |
  |
- |
form drag |
  |
- |
friction factor |
  |
- |
averaged value
  over
over
  |
  |
- |
value
  ,
averaged over ,
averaged over
  in a REV
in a REV
  |
  |
- |
value f morpho-fluctuation in a
  |
  |
- |
gravity
 ![$[m/s^{2}]$](99fluid_5_webfor__24.gif) |
  |
- |
buoyant production / destruction |
  |
- |
turbulent kinetic energy
 ![$[m^{2}/s^{2}]$](99fluid_5_webfor__27.gif) |
  |
- |
fluid thermal conductivity
[  ] ] |
  |
- |
averaged turbulent eddy viscosity
[  ] ] |
  |
- |
integral length scale of turbulence |
  |
- |
porosity [-] |
  |
- |
pressure
[  ] ] |
  |
- |
specific surface of a porous medium
  |
  |
- |
  |
  |
- |
cross flow projected area of obstacles
[  ] ] |
  |
- |
internal surface in the REV
[  ] ] |
  |
- |
temperature
 ![$[K]$](99fluid_5_webfor__47.gif) |
  |
- |
velocity in x-direction
 ![$[m/s]$](99fluid_5_webfor__49.gif) |
  |
- |
square friction velocity at the interface surface
 ![$[m^{2}/s^{2}]$](99fluid_5_webfor__51.gif) |
  |
- |
mean velocity
 ![$[m/s]$](99fluid_5_webfor__53.gif) |
  |
- |
velocity in z-direction
 ![$[m/s]$](99fluid_5_webfor__55.gif) |
  |
- |
space coordinate
 ![$[m]$](99fluid_5_webfor__57.gif) |
Subscripts
  |
- |
fluid phase |
  |
- |
component of turbulent vector variable |
  |
- |
laminar |
  |
- |
solid phase |
  |
- |
turbulent |
Superscripts
  |
- |
value in fluid phase averaged over the REV |
  |
- |
mean turbulent quantity |
  |
- |
fluctuation turbulent quantity |
Greek letters
  |
- |
averaged heat transfer coefficient over
 
 ![$[W/(m^{2}K)]$](99fluid_5_webfor__68.gif) |
  |
- |
thermal coefficient of volume expansion
 ![$[K^{-1}]$](99fluid_5_webfor__70.gif) |
  |
- |
representative elementary volume (REV)
 ![$[m^{3}]$](99fluid_5_webfor__72.gif) |
  |
- |
pore volume in a REV
 ![$[m^{3}]$](99fluid_5_webfor__74.gif) |
  |
- |
solid phase volume in a REV
 ![$[m^{3}]$](99fluid_5_webfor__76.gif) |
  |
- |
turbulent coefficient exchange ratio
  [-]
[-] |
  |
- |
turbulent coefficient exchange ratio
  [-]
[-] |
  |
- |
kinematic viscosity
 ![$[m^{2}/s]$](99fluid_5_webfor__82.gif) |
  |
- |
density
 ![$[kg/m^{3}]$](99fluid_5_webfor__84.gif) |
  |
- |
dissipation rate of turbulent kinetic energy |
  |
- |
wall shear stress
 ![$[N/m^{2}]$](99fluid_5_webfor__87.gif) |
1. Introduction
Turbulence modeling, a part of computational fluid dynamics, emerged as a
distinct discipline and in conjunction with suitable numerical methods, became
one of the more widely employed predictive tools in fluid mechanics and in
heat and mass transfer. Using turbulent models to predict turbulent flow and
related heat transfer in porous media is still in its infancy. Lee and Howell
(1987) proposed a

 model for flow through porous media with high porosity using the same eddy
viscosity for the porous media as one which is commonly used for a pure fluid.
Turbulent transport equations for porous media were developed by Primak et al.
(1986), Shcherban et al. (1986) and Travkin and Catton (1992, 1993, 1995)
based on the generalized Volume Averaging Theory (VAT) for highly porous media
along with the statistical and numerical methodology needed for their
solution. Simplified
model for flow through porous media with high porosity using the same eddy
viscosity for the porous media as one which is commonly used for a pure fluid.
Turbulent transport equations for porous media were developed by Primak et al.
(1986), Shcherban et al. (1986) and Travkin and Catton (1992, 1993, 1995)
based on the generalized Volume Averaging Theory (VAT) for highly porous media
along with the statistical and numerical methodology needed for their
solution. Simplified

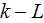 models based on approaches taken in meteorology and agro-science were used in
these works. Antohe and Lage (1997) presented a two - equation
models based on approaches taken in meteorology and agro-science were used in
these works. Antohe and Lage (1997) presented a two - equation

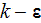 turbulence model for incompressible flow within a fluid saturated and rigid
porous medium that is the result of incorrect procedures. Masuoka and Takatsu
(1996) proposed a 0 - equation model for the turbulent flow through porous
media consisting of packed spheres.
turbulence model for incompressible flow within a fluid saturated and rigid
porous medium that is the result of incorrect procedures. Masuoka and Takatsu
(1996) proposed a 0 - equation model for the turbulent flow through porous
media consisting of packed spheres.
In spite of many achievements in mathematical modeling of turbulent flow in
porous media, there are still some physical effects that are not well modeled
leaving the porous media research community without satisfactory tools. The
motivation of this paper is to develop a more complete and rigorous model for
the

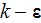 equations in porous media based on the VAT methods (see Travkin and Catton,
1998; and Whitaker, 1997).
equations in porous media based on the VAT methods (see Travkin and Catton,
1998; and Whitaker, 1997).
2. Incompressible flow

 -
-

 model in Porous Media
model in Porous Media
Three types of turbulence models can be identified as approximate engineering
methods or models. They are the two-equation Eddy-Viscosity Models (EVMs), the
differential Re-stress equation model (DSM) and intermediate (truncated) and
''hybrid'' models. Among the above possible models for turbulent momentum in
porous media, two - equation EVMs in their rudimentary forms have a major
advantage in their simplicity and practical usability. We will try to maintain
the blend of simplicity and acceptable predictive ability of popular models
such as the

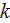 -
-
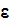 models and employ them for the computation and predictions of turbulent flows,
heat and mass transfer and associated transport phenomena in porous media. The
existing closure equations for the
models and employ them for the computation and predictions of turbulent flows,
heat and mass transfer and associated transport phenomena in porous media. The
existing closure equations for the

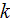 -
-
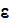 equations will be our starting point. For steady state incompressible flow,
the transport equation determining the distribution of turbulent kinetic
energy (TKE)
equations will be our starting point. For steady state incompressible flow,
the transport equation determining the distribution of turbulent kinetic
energy (TKE)

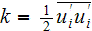 derived
by Rodi (1984) reads
derived
by Rodi (1984) reads
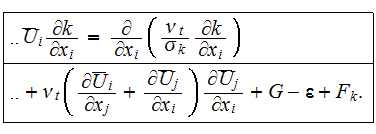
It can also be written in the form
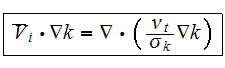
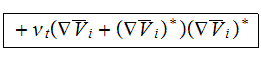
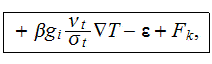
where

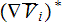 is the transposed dyadic.
is the transposed dyadic.
Following the averaging scheme presented by Travkin and Catton (1992), the
averaged forms of the two factor terms in the turbulent kinetic energy
equation are
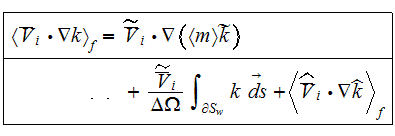
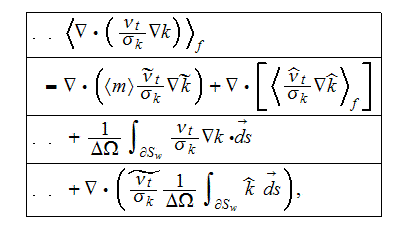
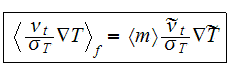
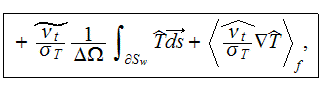
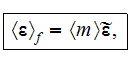
The term with the triple factor-operator product is
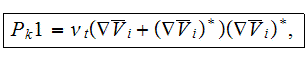
which is the kinetic energy production term. In order to derive the averaged
form of this term, first simplify the product of tensors

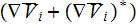 and
and

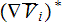
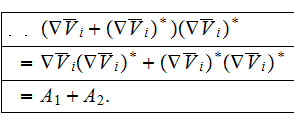
where
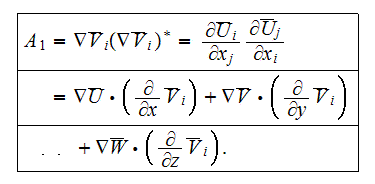
As long as the partial derivatives

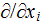 can be presented as
can be presented as
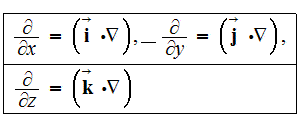
which in turn transforms the partial derivatives
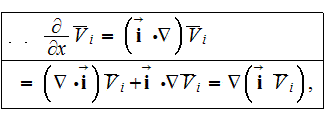
where

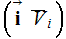 is the dyadic. Similarly, the other two vectorial variables take the form as
is the dyadic. Similarly, the other two vectorial variables take the form as
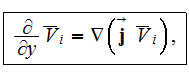
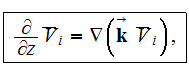
then Eqn.( ) can be expressed as

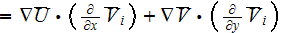
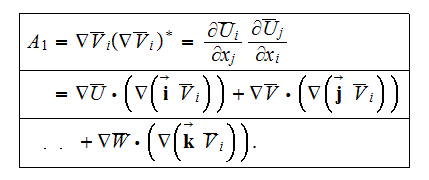
The second term

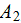 in Eqn.() is a product of tensors
in Eqn.() is a product of tensors

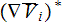 and will be of the form
and will be of the form
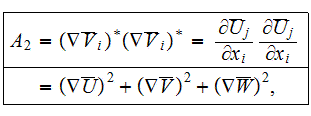
Averaging of the above operators involves averaging the triple
product-operator terms . The general triple product decomposition averaging is
formulated as
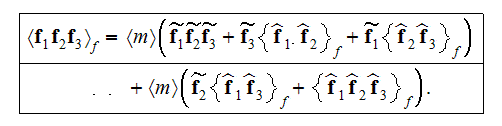
With this as guidance, the needed averaged terms can be obtained. For example,
for the additive term
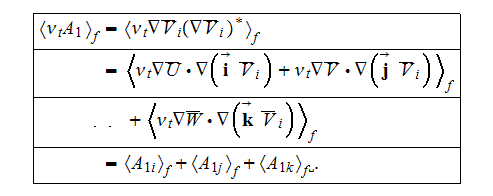
is derived by assigning
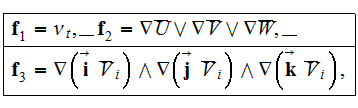
For the term

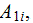 one obtains
one obtains
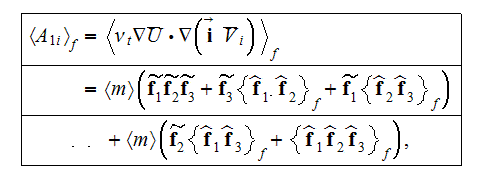
where
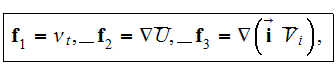
with averaged and fluctuation variables
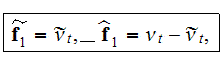
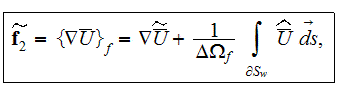
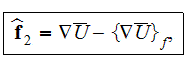
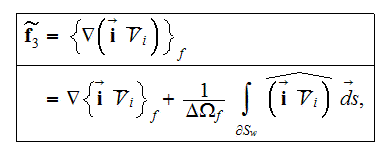
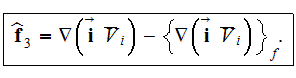
The same process is applied to the averaged operators

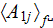 and
and

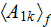 .
Applying this technique to the averaging of term
.
Applying this technique to the averaging of term

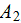 yields the following formulae
yields the following formulae
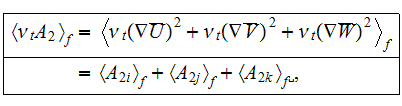
where similar averaging procedures give three more scalar triple operand terms
in the averaged

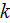 equation
equation
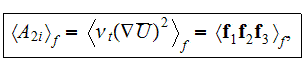
where
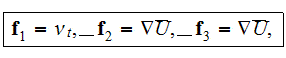
with averaged and fluctuation variables
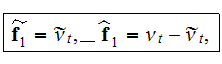
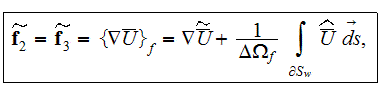
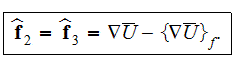
Substitution of

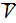 and
and

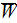 for
for

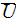 when averaging
when averaging

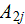 and
and

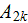 in the above formulae substitution is the only difference between these terms.
By combining all six terms that describe averaged production terms in the
equation for turbulent kinetic energy transport in porous media, one can write
in the above formulae substitution is the only difference between these terms.
By combining all six terms that describe averaged production terms in the
equation for turbulent kinetic energy transport in porous media, one can write
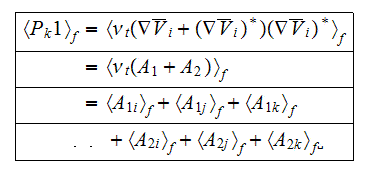
The averaged turbulent kinetic energy transport equation will be
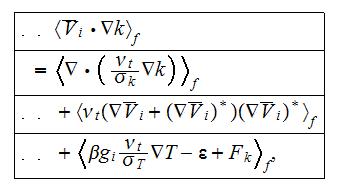
or
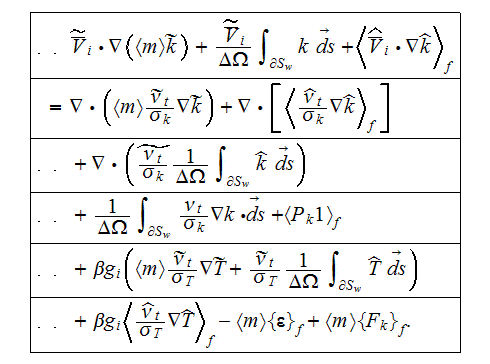
A similar transformation can be justified for the steady state

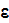 equation
equation
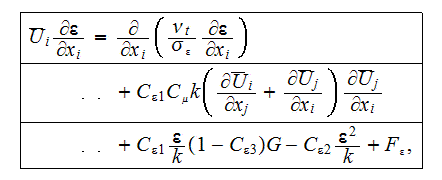
or
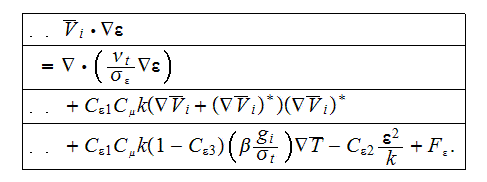
Following the same averaging procedures outlined above leads to the final form
of the averaged dissipation rate equation,
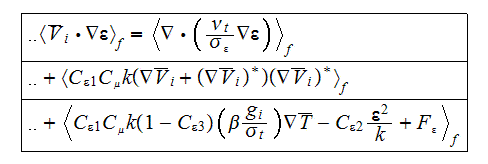
or

A reasonable assumption to take the equality for the turbulent viscosity as
for the averaging procedure
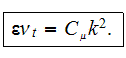
which after averaging becomes
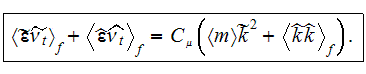
3. Turbulent

 -
-

 Model for Porous Media
Model for Porous Media
Closure is needed for practical application of the equations presented in the
previous section. The closure scheme given below for the

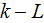 model equations may serve as guidance for finding closure for the
model equations may serve as guidance for finding closure for the

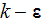 model equations.
model equations.
According to Monin and Yaglom (1975), the transport equation for the kinetic
energy of the mean motion

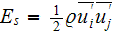 is
is
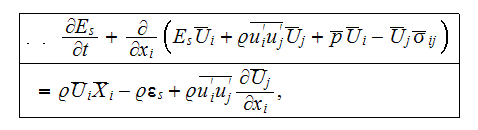
where
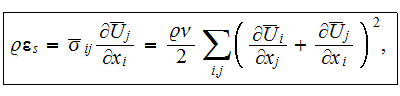
denotes the rate of dissipation of energy of the mean motion under the action
of molecular viscosity. The first term on the right hand side,

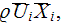 the loss of the kinetic energy due to interaction with the obstacles in the
mean stream, can be accounted for by complete transformation to fluctuation
kinetic energy
the loss of the kinetic energy due to interaction with the obstacles in the
mean stream, can be accounted for by complete transformation to fluctuation
kinetic energy

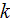 because there are no other sources or sinks for the fluctuation motion kinetic
energy. Thus
because there are no other sources or sinks for the fluctuation motion kinetic
energy. Thus
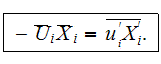
The one-dimensional equation for momentum flux in a flat channel filled with
regular porous medium, under steady-state conditions and certain other
simplifications, with no flow penetration through

 ,
has the following form for a horizontally homogeneous stream (Travkin and
Catton, 1992, 1995)
,
has the following form for a horizontally homogeneous stream (Travkin and
Catton, 1992, 1995)
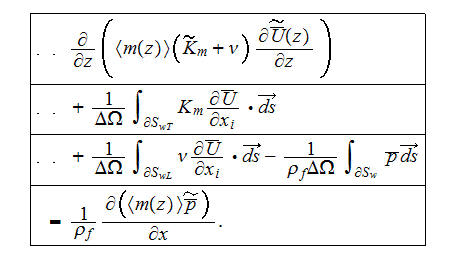
The integral friction resistance terms in momentum equation are
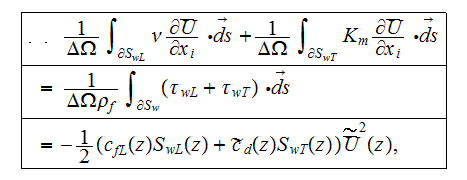
where
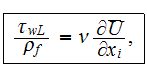
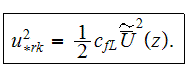
The pressure drag resistance integral term is closed in a manner similar to
that for a one component pressure resistance coefficient over a single
obstacle,
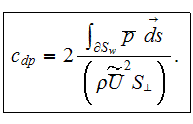
The result is
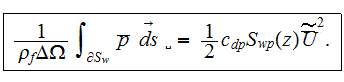
The general volume force is represented by
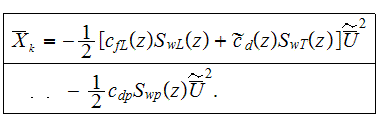
The influence of the volume drag resistance forces within the porous media on
the turbulent fluctuation energy balance is taken into consideration by
considering the contribution of pulse type drag forces. Assuming that most of
the mean motion kinetic energy lost due to interaction of the flow with the
porous medium solid obstacles translates into increasing of the turbulent
fluctuation energy ( Monin and Yaglom, 1975; Menzhulin, 1970) brings one to
the conclusion that
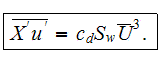
A term like this in the kinetic energy equation accounts for the influence of
additional volume momentum resistance forces.
4. Conclusions
Mathematical models for modeling momentum transport in a porous media are
developed using volume averaging theory (VAT) methods. These models use

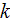 -
-

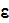 and
and

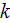 -
-

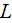 fluctuation equations at the lowest level for closure of the subdomain
homogeneous turbulent transport description. Averaging procedures performed
over highly nonlinear components of those equations leads to the complicated
final forms of the equations. Comparison with previous work and closure
examples are given. Not withstanding the complicated appearance of kinetic
energy and dissipation rate equations in porous media, the variables involved
are completely described with known averaged variables and their variations.
Subsequent work will use the derived equations in porous media momentum
transport modeling.
fluctuation equations at the lowest level for closure of the subdomain
homogeneous turbulent transport description. Averaging procedures performed
over highly nonlinear components of those equations leads to the complicated
final forms of the equations. Comparison with previous work and closure
examples are given. Not withstanding the complicated appearance of kinetic
energy and dissipation rate equations in porous media, the variables involved
are completely described with known averaged variables and their variations.
Subsequent work will use the derived equations in porous media momentum
transport modeling.
Acknowledgment
This work was partly sponsored by the Department of Energy, Office of Basic
Energy Sciences through the grant DE-FG03-89ER14033 A002.
References
Antohe, B. V. and Lage, J. L., (1997), A General Two-Equation Macroscopic
Turbulence Model for Incompressible Flow in Porous Media,
Int. J. Heat Mass Transfer, Vol. 40, No. 13,
pp. 3013-3024
Lee, K. and Howell, J. R. (1987), Forced Convective and Radiative Transfer
within a Highly Porous Layer Exposed to a Turbulent External Flow Field,
Proc. 2nd ASME/JSME Thermal Engineering Joint Conf
., Vol. 2, pp.377-386.
Masuoka, T. and Takatsu, Y. (1996), Turbulence Model for Flow through Porous
Media, Int. J. Heat Mass Transfer, Vol. 39, No.
13, pp.
2803-2809.
Menzhulin, G. V., (1970), The Method of Calculating the Meteorological Regimes
in the Vegetation Cover, Meteorology and Hydrology,
No. 2, pp. 92-99.
Monin, A. S. and Yaglom, A. M. (1975), Statistical Fluid
Mechanics, J. Lumley (ed.). MIT Press, Cambridge, MA.
Primak, A.V., Shcherban, A.N. and Travkin, V.S., (1986), Turbulent Transfer in
Urban Agglomerations on the Basis of Experimental Statistical Models of
Roughness Layer Morphological Properties, Trans. World
Meteorological Organization Conf. Air Pollution Modelling Application,
Geneva, Vol. 2, pp. 259-266.
Rodi, W. (1984). Turbulence Models and Their Applications in Hydraulics - a
State of the Art Review, International Association for
Hydraulic Research.
Shcherban, A.N., Primak, A.V., and Travkin, V.S. (1986), Mathematical Models
of Flow and Mass Transfer in Urban Roughness Layer,''
Problemy Kontrolya i Zaschita Atmosfery ot
Zagryazneniya, No. 12, pp. 3-10 (in Russian).
Travkin V. S. and Catton, I., (1992), Models of Turbulent Thermal Diffusivity
and Transfer Coefficients for a Regular Packed Bed of Spheres,
Procs., 28th National Heat Transfer Conference, San
Diego, CA, ASME, HTD-Vol. 193, pp. 15-23.
Travkin, V. S., Catton, I., and Gratton, L., (1993), Single Phase Turbulent
Transport in Prescribed Non- isotropic and Stochastic Porous Media,
Heat Transfer In Porous Media, ASME,
HTD Vol. 240, pp. 43- 48.
Travkin V. S. and Catton, I., (1995), A Two Temperature Model for Turbulent
Flow and Heat Transfer in a Porous Layer, Journal of Fluid
Engineering, Vol. 117, pp. 181-188.
Travkin, V.S. and Catton, I., (1998), ''Porous Media Transport
Descriptions-Non-Local, Linear and Non-Linear against Effective Thermal/Fluid
Properties'', Advances in Colloid and Interface Science,
Vol. 76-77, pp.
389-443.
Whitaker, S. (1997), ''Volume Averaging of Transport Equations'', Chap. 1, in
Fluid Transport in Porous Media, Computational
Mechanics Publications, Southampton, UK, 1997.
Copyright © 2001...Thursday, 03-Jul-2025 09:05:12 GMT V.S.Travkin, Hierarchical Scaled Physics and Technologies™

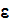 turbulence models are considered to be appropriate for the lowest level of
hierarchical modeling. The fluctuations produced by the porous medium
heterogeneity and wall roughness contribute to the overall transport processes
and to the governing scalar fluctuation equations, the Reynolds stress
equation, the turbulent kinetic energy (TKE) and the dissipation rate of TKE.
These equations must be treated along with other phenomenological
dependencies. In view of the theoretical importance to turbulent transport in
porous media, incompressible turbulent flow within porous media is modeled
using the proper averaging of the transport equations for the turbulent
kinetic energy
(
turbulence models are considered to be appropriate for the lowest level of
hierarchical modeling. The fluctuations produced by the porous medium
heterogeneity and wall roughness contribute to the overall transport processes
and to the governing scalar fluctuation equations, the Reynolds stress
equation, the turbulent kinetic energy (TKE) and the dissipation rate of TKE.
These equations must be treated along with other phenomenological
dependencies. In view of the theoretical importance to turbulent transport in
porous media, incompressible turbulent flow within porous media is modeled
using the proper averaging of the transport equations for the turbulent
kinetic energy
(
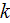 )
and its dissipation rate
(
)
and its dissipation rate
(
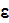 ).The
closures of these model equations are obtained for a few morphologies. The
averaging of these equations is based on strict principles developed for
application of volume averaging theory (VAT). A variety of closure
alternatives are considered for application to the VAT turbulent kinetic
energy and VAT dissipation rate of TKE resulting in a set of simulation
equations. An analysis of other equations used in heterogeneous transport
theories is given for comparison.
).The
closures of these model equations are obtained for a few morphologies. The
averaging of these equations is based on strict principles developed for
application of volume averaging theory (VAT). A variety of closure
alternatives are considered for application to the VAT turbulent kinetic
energy and VAT dissipation rate of TKE resulting in a set of simulation
equations. An analysis of other equations used in heterogeneous transport
theories is given for comparison.




















![$[m/s^{2}]$](99fluid_5_webfor__24.gif)


![$[m^{2}/s^{2}]$](99fluid_5_webfor__27.gif)

















![$[K]$](99fluid_5_webfor__47.gif)

![$[m/s]$](99fluid_5_webfor__49.gif)

![$[m^{2}/s^{2}]$](99fluid_5_webfor__51.gif)

![$[m/s]$](99fluid_5_webfor__53.gif)

![$[m/s]$](99fluid_5_webfor__55.gif)

![$[m]$](99fluid_5_webfor__57.gif)










![$[W/(m^{2}K)]$](99fluid_5_webfor__68.gif)

![$[K^{-1}]$](99fluid_5_webfor__70.gif)

![$[m^{3}]$](99fluid_5_webfor__72.gif)

![$[m^{3}]$](99fluid_5_webfor__74.gif)

![$[m^{3}]$](99fluid_5_webfor__76.gif)





![$[m^{2}/s]$](99fluid_5_webfor__82.gif)

![$[kg/m^{3}]$](99fluid_5_webfor__84.gif)


![$[N/m^{2}]$](99fluid_5_webfor__87.gif)