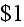investment in such an asset over the time interval
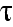grows to
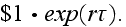Alternatively, if
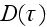is the date
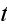price of a discount bond maturing at date
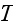with face value
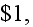then for
![$t\in \lbrack 0,T]$](/finhet/pic/OverAsses__8.gif)
the bond price dynamics are given by
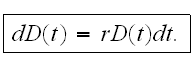
As everyone knows - there is no free lunch, or the cheese is free only in the mouse trap. So to say, we need to talk about the deficiences in the analysis by Black-Scholes and Merton. There were few assumptions put into the basis of the Black-Scholes model and equation.
Those are:
A1) There are no market imperfections, e.g., taxes, transactions costs, shortsales constraints, and trading is continuous and frictionless.
Yes, this is the GREAT assumption.
A2) There is unlimited riskless borrowing and lending at the
continuously compounded rate of return r; hence a
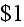investment in such an asset over the time interval
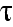grows to
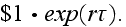Alternatively, if
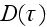is the date
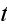price of a discount bond maturing at date
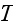with face value
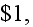then for
the bond price dynamics are given by
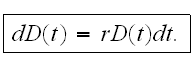
A3) The stock price dynamics is given by a geometric Brownian
motion, with the solution to the following Ito stochastic differential
equation on
![$t\in \lbrack 0,T]$](/finhet/pic/OverAsses__10.gif)
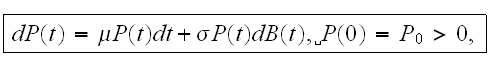
where
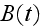is a standard Brownian motion, and at least one investor observes
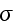without an error.
A4) There is no arbitrage.
