The Science of Coefficients is About the Thing for Which the Most of Experimental Effort Undertaken

Do We Really Care About of How the Experiments are Being Brought Down to Results, Plots, and Conclusions?

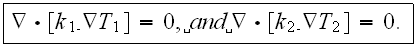
Let's just make a Quick Example:

If we consider the conductivity heat transport in heterogeneous medium, say a composite with the steady-state conduction.

Then we can explore the two basic modes:

1) is the Bottom-Up consideration (experimental set-up and modeling with data reduction). This is the most used mode of calculation of Effective parameters, coefficients. For the two-phase medium we would write the modeling equations for the Lower scale

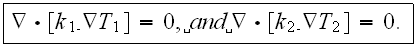
Then we would use the VAT Upper scale averaged variables equations

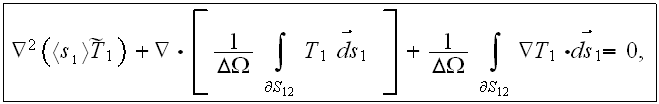
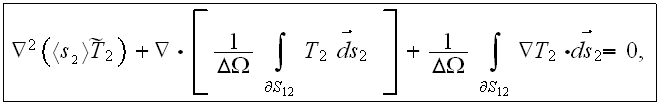
along with the Upper scale effective coefficient statement - IF WE NEED THAT, which is actually the homogeneous medium (Upper scale) equation

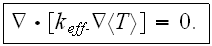
2) Still, probably the most often workers need to address the another direction of values connected - and that is when the Top-Down point of view prevails. Here we have some apriori known or established or experimentally obtained values of characteristics on the Upper spatial scale, and we would like to know which mechanism input's been done into this value while accordingly make the design of experiment. At this time we know approximately or exactly the components of Lower scale process.

If we think at this moment that the lower scale theoretical description of process

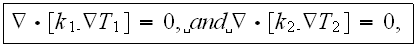
is the same as on the Upper scale

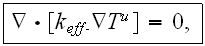
then we have nothing specifically correct to distinguish for Heterogeneous Media. And this is the connection, communication as it has been viewed by most of experimentalists now, especially in chemistry and materials science.

Sometimes this called as a Multiscaling !?

Quite the contrary will be the situation when we know something about the difference of scaled models for heterogeneous media, then we use for the lower scale the two pairs of equations:
a)

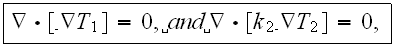
b) and the VAT equations

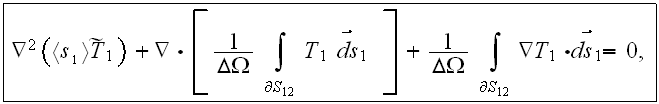
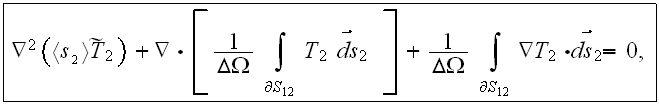
to find out - What is the connection and the quantitative values of characteristics on both scales. This time around we need to understand - What we actually Are measuring?

The Upper scale characteristic or the Lower one still?

Now the problem is to be much more descriptive and can have a numerous aims, than just writing the formula for the "effective conductivity" as

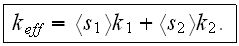
Considering the effective coefficient problem as the cornerstone issue in the heterogeneous media transport, one needs to accommodate the reasoning that the absolute majority of problems stated and studies include the following assumptions:

1) a composite, for example, is a two-phase media consisting of a continuous matrix phase and embedded inclusions of disperse phase;

2) phase materials are homogeneous and isotropic, their properties are temperature-independent;

3) disperse phase consists of the equally sized spherical particles, uniformly distributed within a matrix phase. As a result, the composite is assumed to be macroscopically isotropic;

4) interfaces have the conditions of conventional boundary transport laws, for example, the perfect thermal contact is supposed to exists:

5) there is no way that the specifics of morphology would be used directly in experiment or simulation. Yes, mostly people handling this issue by Artificial hands-on connection between both, but based on the convenient one scale physics model.

Authors of work (Sposito, Jury, and Gupta, 1986) clearly made the distinction between the laboratory columns experimental results and real field physical problems. By analyzing the stochastic convection-dispersion equation (SCDE) statements authors concluded about significanse of number of open questions remained when using SCDE in relatevely simple conditions of non-reactive dissolved solutes.

Many of these questions conjugate with the "scale" challenges involved with these groundwater contamination problems.

Page 77 - from abstract: "It is shown that even the best-developed stochastic CDE models involve physical approximations and mathematical assumptions which stand in need of more rigorous theoretical study and detailed field experimentation. The stochastic convection-dispersion model does not yet resolve clearly the mathematical conditions necessary in order to relate the mean solute concentration calculated with a field scale stochastic CDE to measured values of the solute concentration determined in a single field experiment."

Page 78 - "Experiments on the transport of relatively non-reactive dissolved solutes (e.g., halides) through soil and aquifer materials have been modeled for many years by the partial differential equations [Biggar and Nielsen, 1967; Bear, 1972]:

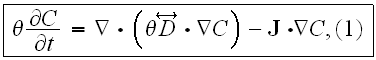
where is the concentration of solute in an aqueous solution whose volumetric content in a porous medium is 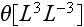and whose volumetric flux density through the medium is 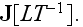The elements of the second-rank tensor 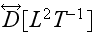are known as solute dispersion coefficients and (1) is called the convection-dispersion equation.

The rigorous derivation of (1) from microscpic or molecular physical principles remains an open research problem......" ??

On page 82 they wrote: "Specifically, if 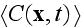at large times satisfies the Fickian approximation, then it can be expressed as a solution of the following classical CDE:

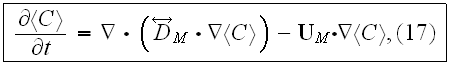
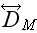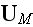where and are uniform, constant, nonrandom parameters for solute transport at the field scale."

Sposito, G., Jury, W.A. and Gupta, V.K., "Fundamental Problems in the Stochastic Convection-Dispersion Model of Solute Transport in Aquifers and Field Soils", Water Resour. Res., Vol. 22, No. 1, pp. 77-88, (1986).