ARPA 1994-95 Project - "Two-phase Contaminant Transport Simulation in Five-Scale Saturated Soil Systems"
ABSTRACT
The project is aimed to find the real physically grounded way to model and simulate the transport of contaminated groundwater and nonconservative solute in saturated soil systems (SSS). Since that no one model exists at present time that could accounting on multiscaled morphology consideration, the suggested development will deal with flow and solute modeling in five scale soil systems, including : 1- solid-liquid surface scale modeling; 2 - pore scale; 3 - first (small) scale homogeneous porous medium two phase and two-concentration modeling; 4 - second (large) scale heterogeneous porous layer modeling; 5 - finally transport modeling in multiple layer confined or unconfined SSS. To obtain that kind of models must be used and significantly improved multiscale morphological modeling approach that has been developing by one of the principal key personnel. Modeling procedures is believed will make the more accurate and physical model's output while considering the transport of constituents in each of the phase on each of the level of hierarchy. After being developed this kind of models would be advantageous in comparisons with existing models by its close ties and dependence of given site the soil and multiscale morphology. This should bring the soil and groundwater modeling science on the next level of development.


The Final report's texts are given here with omissions due to length of the document, some parts
are more cumbersome and not obvious to a reader, also SOME PARTS ARE UNSURPASSED UP TO NOW.
TABLE OF CONTENTS
ABSTRACT......................................................................... ................................................. i
LIST OF FIGURES........................................................................... .................................... iv
LIST OF TABLES............................................................................ .................................... vii
SYMBOLS AND ABBREVIATIONS........................................................ .......................... viii
SUMMARY OF THE PHASE 1 RESULTS................................................... ...................... 13
INTRODUCTION..................................................................... ............................................ 17
1. ANALYSIS AND MODELING OF VARIOUS LEVEL GROUNDWATER
TRANSPORT PHENOMENA ............................................................................ ............ 19
1.1 SOIL STRUCTURE STATISTICS ........................ .......................................................................... 19
1.2 SOIL MORPHOMETRICAL ANALYSIS ...................................................... ............................... 24
1.3 COLLOIDAL TRANSPORT.... ........................................................................ ............................... 32
1.4 NANO- AND MICROSCALE PHENOMENA........................................................ ...................... 34
1.4.1 INFLUENCE OF BOUNDARY LAYER OF THE LIQUIDS ON MASS
TRANSPORT IN FINE PORES ......................................................................... ..............34
1.4.2 FLOW IN CURVED PORES ........................................................................ ................. 40
1.5 INTERFACIAL SURFACE SORPTION .................................................. ........................................ 46
1.6 NONLINEAR TRANSPORT ON PORE LEVEL.... ......................................... ............................... 51
1.7 NONLINEAR TRANSPORT EQUATIONS ............................................ ........................................ 60
1.7.1 LINEAR AND SEMILINEAR AVERAGED LAMINAR REGIME TRANSPORT
EQUATIONS IN POROUS MEDIA ...................................................................... .........60
1.7.1.1 CREEPING FLOW ...... ......................................................................... ....... 60
1.7.1.2 LAMINAR FLOW WITH CONSTANT COEFFICIENTS .......................... 81
1.7.2 NONLINEAR FLUID MEDIUM TRANSPORT EQUATIONS IN LAMINAR
FLOW....................... ........................................... ............................................................. 89
1.8 FOURTH LEVEL APPROACH. HEAT AND MASS TRANSFER BOUNDARY
CONDITIONS BETWEEN TWO MEDIA... .................................................................................... 97
1.9 FIFTH LEVEL LOCAL FIELD MODELING............................................... ................................... 101
2. PROJECT FEASIBILITY MODELING....................................................... ..................... 103
2.1 INTRODUCTION................................................................... ........................................................... 103
2.2 RESEARCH DATABASE DEVELOPMENT ................................................. ................................ 103
2.3 SINGLE PORE TRANSPORT MODELING ................................................ ...................................108
2.3.1 INTENSE AND TURBULENT TRANSPORT IN ROUGH PORE ........ .................... 108
2.3.2 LAMINAR REGIME ROUGH PORE TRANSPORT ................................................... 127
2.4 MICROSCALE NETWORK MODELING ...................................................................................... 137
2.5 STRAIGHT PORE MORPHOLOGY MATHEMATICAL MODEL DEVELOPMENT ............... 144
2.6 RANDOM DISTRIBUTION PORE SIZE MORPHOLOGY .......................................................... 149
2.6.1 NEWTONIAN GROUNDWATER VISCOSITY MODELING .................................... 152
2.6.2 NON-NEWTONIAN CONTAMINATED FLUID TRANSPORT ................................ 161
2.7 THEORETICAL ANALYSIS OF FLOW AND TWO-TEMPERATURE POROUS MEDIUM
MODELING EQUATIONS................................................................................................................ 169
2.7.1 NONLINEAR UNIFORM POROSITY EQUATIONS ................................................. 169
2.7.2 WEAKLY NONLINEAR EQUATIONS FOR NONUNIFORM POROSITY .............170
2.7.3 STRONG NONLINEARITY AND SLOWLY VARYING NONUNIFORMITY IN
POROSITY........................................................................................................................ 171
2.8 UNCERTAINTY ANALYSIS ........................................................................................................... 173
2.9 SOFTWARE SYSTEM DESIGN........................................................................................................178
3. CONCLUSIONS ............................................................................................................... 184
4. REFERENCES ................................................................................................................. 188
5. PHASE II PROSPECTUS ................................................................................................. 201
SUMMARY OF THE PHASE 1 RESULTS
The feasibility study was carried out in two parts. First, various aspects of groundwater phenomena were addressed. The second part of the study dealt with feasibility. A number of results were obtained. These results are summarized for each part of the study.
The following analysis results confirmed that morphometrical soil characteristics should be an ingredient in local site assessment and used in the multiscaled modeling methodology:
M In fine pores, it was found that due to polymorphism of the surface fluid layers the modeling should use the structured near surface film of liquids because it is different from that of the bulk liquid. The modified structure of contaminated water was shown to affect the filtration process and leads to inapplicability of the Darcy law.
M Analysis revealed that calculations of the flow rates must account for the dependence of viscosity on distance from the pore wall. As long as the water boundary layers at nanoscale distances from the solid phase are characterized by elevated viscosity and do not display a noticeable critical shear stress, they are important.
M For circumstances where sorption from contaminated groundwater to the solid surfaces of soil and minerals plays the major role in the distribution and fate of organic pollutants in the soil and groundwater contamination system (SGCS), reasonable phenomenological descriptions of adsorption using the specifics of the current approach were achieved.
M The theory of volume averaging (VAT) has been applied directly to develop second and third level transport equations.
M A dual-porosity "near" pore model was developed featuring a random and irregular interface surfaces (random surface morphology), permeable solid phase model for transport of momentum, mass and heat with the correct boundary conditions on the pore (crack) surface.
Part II. Modeling
The goal of this part of the study was to develop the different research modeling elements. The specific results are the following:
M A computer code for rough crack (or large pore) momentum and heat transport has been produced and transport processes in a rough pore with different morphological types of roughness were simulated.
M A second code for rough pore modeling of the laminar momentum transport regime has been developed. The results of a numerical simulation were obtained and analyzed for both regimes.
M The development of a prototype network momentum computer code has been completed and preliminary results have been obtained. This is the initial step in modeling of a groundwater network at the 3d level. We plan to use these results in our implementation of the next level of the transport equations. Several network morphologies at millimeter scale were studied by computer simulation.
M Simulation of capillary networks consisting of nodes (various junctions) and pores to model function fluctuations and to use them in closure equations was accomplished. Two computer programs were produced. One simulates very low momentum transport while the other focuses on the non-linear analysis of a capillary network. This effort resulted in a different approach for flow resistance calculations.
M Formulation of equations and mathematical models for straight pore morphologies in the 1D was accomplished using capillary closure solutions for research purposes.
M A random pore diameter morphology model was developed and implemented in a computer code. The objective of this modeling was to determine the impact of a random pore distribution on averaged and fluctuation values of momentum and heat transfer.
M A non-Newtonian fluid model has been introduced for use with the specific capillary morphology. Simulation results show the importance of non-Newtonian viscosity model in the modeling of bulk and local transport characteristics.
M Analysis of closed forms of the porous medium transport equations developed in this work was accomplished. These equations usually incorporate two features: nonlinearities of different kinds and nonuniformity of porosity.
M Analytical solutions and evaluation of some simplified transport equations yielded the tools for analysis of the influence of nonlinearity and nonuniformity of porosity.
M The most sensitive parameters in the equations of slow flow of contaminated groundwater in the soil were identified. A sensitivity analysis allowed us to identify the parameters with the highest impact on the final results.
M The design of the Model Software System (MSS) was developed based on a Top-Down design methodology.
INTRODUCTION
Analysis of scale phenomena, formulation of principles and the development of a basic set of equations for transport modeling at the lowest levels of a Soil and Groundwater Contamination System (SGCS) were accomplished during the feasibility study. The focus of the current project was to create the modeling capabilities needed to deal with many of ignored phenomena and to develop new multilevel models for the needed SGCS. As a result, the theoretical approach did not focus on overcoming the principal difficulties of modeling fine scale SGCS phenomena, such as physics of colloid transport or solid-liquid physico-chemical interface phenomena.
The time allotted to the Phase I effort limited the investigation of the different areas pertinent to this project to various degrees of thoroughness. In some areas, however, completely new results were obtained, e.g.: 1) rough pores transport modeling; 2) nonlinear models development; 3) mathematical study of transport processes new equations; 4) nano - and microscale model development including the using of new polar liquids viscosity model; 5) random capillary morphologies and 2D network morphologies modeling; 6) uncertainty approach to the present theory mathematical statements.
The complete of mathematical derivations are not presented elsewhere in this report. Some of the theoretical developments were recently published, some are too lengthy and detailed, while others are not essential. Modeling of the key elements of the current theory like pore level structures, nonlinear effects and morphological closure revealed many features that were not known before and the need the more detailed study. In spite of the known existence of other approaches to rough channel transport modeling e.g. particular FEA application, it is worth noting that there is no meaningful method for describing random, stochastic distributions of roughness elements parameters other than that developed in this (and prior) VAT work.
The first part of the Phase I project final report contains the soil morphological analysis, some treatment of nano- and microscale physical phenomena, theoretical modeling at the pore level, and development of the averaged nonlinear transport equations for the first three levels of the SGCS. Part II of the report contains the project feasibility modeling. Here a number of different aspects of modeling of groundwater transport phenomena are addressed. First, a database was constructed in a way it could be kept on a PC. Second, a series of the necessary elements of a model are treated. Third, the equations necessary for analysis of flow in a two-temperature porous media are developed and analyzed. Then an uncertainty analysis is carried out and finally the design of the software system is described.
1. ANALYSIS AND MODELING OF VARIOUS LEVEL GROUNDWATER TRANSPORT PHENOMENA
The first part of the Phase I final report primarily describes the accomplishments having been made while developing the theoretical basis of the suggested approach. Each task led to the accomplishment of goals described in the following chapters.
1.1 SOIL STRUCTURE STATISTICS
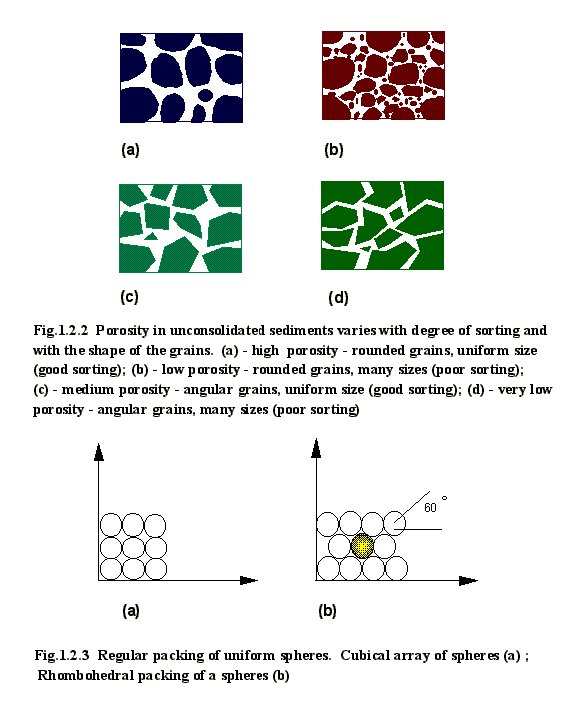
This six orders of magnitude in the effective particle diameters emphasizes the inappropriateness of modeling subsurface soil systems as a homogeneous one - structured ( dispersed ) medium.
The classification criteria developed by Dubinin (see Kheifets and Nejmark, 1979) includes macropores having pores with an effective radius of 100 nm, mezopores having pores with the radius between 15 nm and 100 nm and micropores having pores with a radius less than 1 nm. This classification is strongly tied to the sorption theory point of view because sorption processes on micropore bodies have some outstanding features that will impact the solution process (Gregg and Sing, 1982).
1.2 SOIL MORPHOMETRICAL ANALYSIS
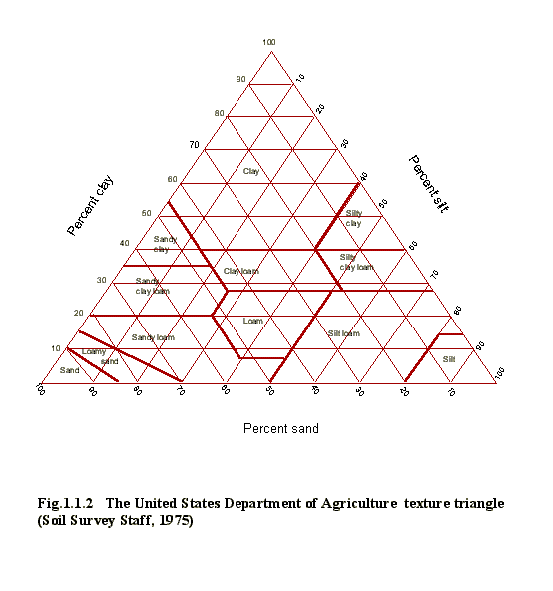
Few of the conclusions of this part of study are:
a) The pore size distribution does not follow the particle size distribution, it is bimodal with the large pore mode depending on the silt or sand fraction, and the small pore mode depending on the clay fraction;
b) The large pore mode depends on the mean particle size and on the clay structure. The small pore mode depends only on the clay particle size;
c) The amplitude of the modal points depends on the clay and sand ( or silt) contents;
d) The width of the distribution about the pick points depends on the PSD and the clay structure.

RECOMMENDATIONS AND CONCLUSIONS
The recommendations and conclusions resulting from the analysis and modeling of groundwater transport phenomena are the following.
1) Basic subsurface soil types and their physico-chemical characteristics should be incorporated into a database to be used as a supplemental modeling tool. Conceptual decision making procedures are being designed for each level of the model hierarchy. We will assume for our purposes that soil characteristics such as saturated hydraulic conductivity, clay content, bulk density, available soil water content be admitted as classification criteria. These and others parameters of the mining layer will serve as a characterization vector in model selection and for model tuning procedures.
2) It is possible the USDA classification and database to divide a ground water aquifer into homogeneous hydrogeological and hydrochemical zones. The USDA classification and database are basis for investigation underground water flow at a local scale. Though it does not avoid the necessity for studying the hydrogeological information about a region.
3) At the pore size scale, particle size distribution (PSD) of the soil samples should be used. This information is always available or can be obtained. For a clay-sand or clay-silt mixture with more than 10% clay, pore size distribution curves will be bimodal and it is possible use PSD to estimate this distribution.
4) For the well-sorted sand or silt with round grains, a model of ideal packing for the spheres or model of slit with rounded obstacles will be useful. Such a model can represent alluvial sedimentation, rock or dune sand. For a rock having angular grains, gravel or angular coarse sand, a model based on a slit with angular obstacles is recommended. The fluid velocity in gravel and coarse sand can reach relatively high values and intense or turbulent flow in such rock is possible.
1.3 COLLOIDAL
TRANSPORT
One of the reasons why colloidal transport should be included in the present modeling effort is the large enhancement of colloidal sedimentation transport in a porous media. This effect has experimental confirmation and should be of great interest. It is worth noting that the convenient non-Newtonian effective viscosity models do not cover the more complex and cumbersome effects of bacteria transport in aquifers.
1.4 NANO- AND MICROSCALE PHENOMENA
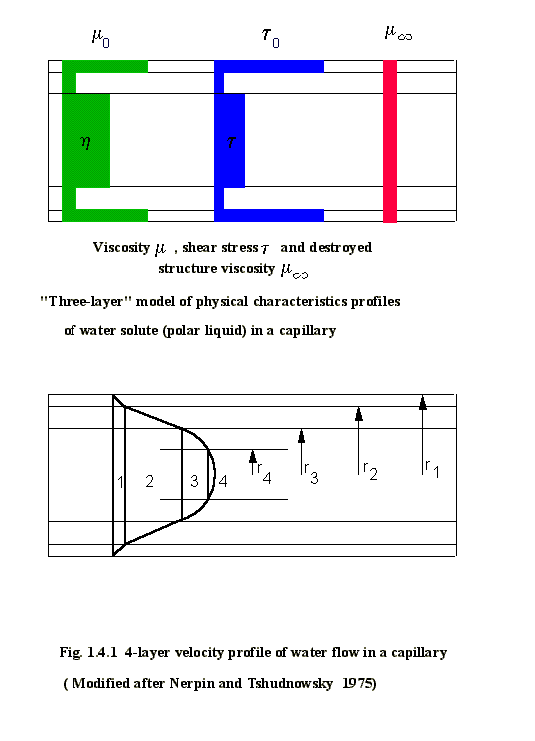
CONCLUSIONS
1) Analysis has confirmed that even for the finest pores (fractions of angstroms), the length scale of the groundwater flow is large compared to the molecular mean-free path. As a result, the fluid can be treated as a continuum in the smallest volumes between the elements of the roughness layer of the pore. However, it should be emphasized, that in fine pores, the structure of liquids is different from that of the bulk liquid due to polymorphism of the surface fluid layers.
2) The modified structure of contaminated water affects the filtration process and leads to inapplicability of the Darcy law. Concerning the applicability of the different forms of the governing equations in irregular curved pores, the first stage of analysis revealed that for pores with curvature the governing equations have two parameters which characterize the flow. The first, the Dean number is equal to the ratio of the square root of the product of the inertia and centrifugal forces to the viscous force. The second parameter is the ratio of the pore radius to its radius of curvature.
3) It is shown that the main effect of curvature is to reduce the momentum flux along the pore. The influence of curvature on flow is evaluated in terms of these two parameters and in most cases this curvature effect could be neglected. Further, the flow in a curved pore is much more stable than in a straight pore. So, while the critical Reynolds number for the latter typically could be about 2000, in a curved pore, of even small curvature, it may be larger by a factor of two or more. It shown that for velocities under consideration the effect of curvature is less than 0.1%. The effect of pore roughness on the transition number is rather uncertain.
4)
Calculations of the flow rates in our models must take into account the
dependence of viscosity on distance from the pore wall. Water boundary layers
at nanoscale remoteness from solid phase are characterized by elevated
viscosity and do not display a noticeable critical shear stress. Measurements
of water flow velocity in capillaries at a number of radii (
ranging from 5x10-2 :m
to 1 :m
) have been used to determine the
1.5 INTERFACIAL SURFACE SORPTION
CONCLUSIONS
1) As long as sorption from contaminated groundwater to a solid surface of soil and minerals plays the major role in the distribution and fate of organic pollutants in the SGCS, work must be devoted to developing reasonable phenomenological descriptions of adsorption. The specifics of the mineral and pollutants composition prescribe the possibility for attaining a sorption equilibrium.
2) The type of sorption of organic compounds depends greatly on the soil (mineral) organic matter content and ion-exchange for some mineral compositions. Computation of equilibrium compositions for simple aqueous solutions - solid phase interfaces should be the goal of a separate software development program if known codes (for example, MINEQL, MINTEQ etc.) are found not applicable.
3) When the interfacial surface morphology is rough and the surface is energetically heterogeneous, the diffusion and adsorption processes become more and more complex. This condition is a common situation at many scales, from nanometer up to millimeter and even centimeter sizes of the surface inhomogeneity.
1.6 NONLINEAR TRANSPORT ON PORE LEVEL
CONCLUDING REMARKS
1) The theory of volume averaging (VAT) has been applied directly to the development of second level transport equations. Spatial scales for the channel's hydraulic diameter must be in the range from 10-9 m to 10-3 m if the flow regime studied is to be in the creeping or laminar regimes. The result is a low-Reynolds number turbulent specific modeling system for flow in a cracked soil, often describes a dual-porosity material with the main channel sizes being on the order 10-3 - 10-2 m. In one of the versions of the model, the solid phase has an impermeable random surface.
2) Another model allows the solid phase to be a porous medium with completely different morphological and transport features. This kind of medium will give us a new benchmark test model to study transport in a dual-porosity medium. Such a dual-porosity modeling is not completely unknown, however, but for the most part they have been implemented with incorrect mathematical statements.
3) The research goal was to develop a dual-porosity "near" pore model and computer code featuring a random and irregular interface surface (random surface morphology), permeable solid phase model for transport of momentum, mass and heat with the correct boundary conditions on the pore (crack) surface. This goal was achieved.
1.7 NONLINEAR TRANSPORT EQUATIONS
The
averaged equations of porous media transport with different kinds of
nonlinearities have been developed in this chapter.
1.7.1 LINEAR
AND SEMILINEAR AVERAGED LAMINAR REGIME TRANSPORT EQUATIONS IN POROUS MEDIA
Creeping
flow momentum transport Stokes equations with permeable interface surface and
two phase mass - and heat convective transport equations were originated.
....................
..........................................................
......................................................
1.7.2 NONLINEAR FLUID MEDIUM EQUATIONS
IN LAMINAR FLOW
To properly account for Newtonian fluid flow phenomena
within a porous media in a general way, modeling should begin with the Navier-Stokes equations for variable fluid properties,
rather than the constant viscosity
Navier-Stokes equations. ............................
CONCLUSION
The
equations for the nonlinear creeping and laminar flow regimes have been
developed for the second and third levels of the SGCS. The permeability of the
two conjugated porous media was fully taken into account. Hierarchial
VAT methods lead to three sets of governing equations for momentum, mass and
heat equations for each morphologically different subdomain.
The permeability of the interfaces arises as long as
it is necessary to treat nonlinear equation forms in mastering the needs of the current
project research and certain commercial goals.
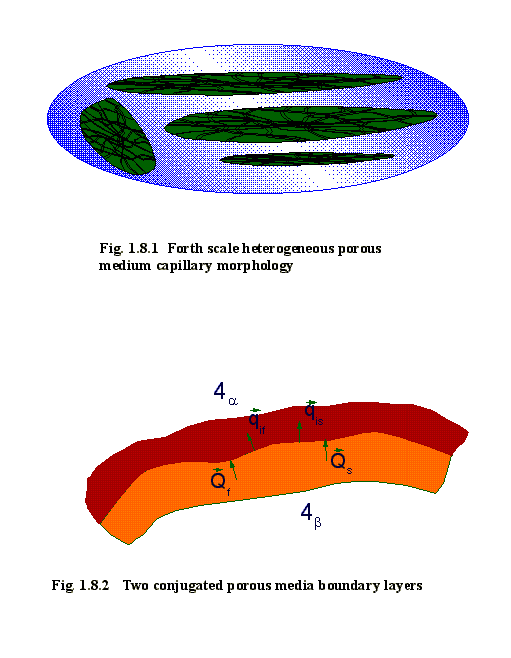
1.8 FOURTH
LEVEL APPROACH. HEAT AND MASS TRANSFER BOUNDARY
CONDITIONS BETWEEN TWO MEDIA
One
of effective closure procedures in the fourth level of the model (Fig.1.8.1) is
to present ("close") all diffusive terms under differential sign in
corresponding transport equations so equivalent effective coefficients in
corresponding 4th level equations yield, by the overall representation of
diffusive and "diffusion-like" terms, for example, in momentum
equation of the 4th level effective diffusion gradient component might be
evaluated through the expression
For problems with a non-fluctuating bulk viscosity
coefficient (Km = constant) the second term in this relation
vanishes and the whole problem essentially reduces to evaluating the influence
of dispersion by irregularities in the soil medium on the momentum. .......
The
above expression is obtained by allowing Ti = averaged variable,
meaning that the temperature of the skeleton on the boundary z = 0 coincides
with the temperature of the interface at the given horizontal (x)
position. It has been shown that for
large Reynolds numbers, where the thickness of the viscous boundary layer does
not exceed the pore size, heat transfer from the wall to the fluid in passages
near the wall is practically equal to the heat transfer from the skeleton
particles to the fluid (Travkin and Catton, 1995b).
1.9 FIFTH
LEVEL LOCAL FIELD MODELING
The
model hierarchy and it ability to treat the details of the soil morphology are
the present model features that determine the model algorithmic and decision
making methodology. The morphology of the fifth level (Fig. 1.9.1) underground
environment determines the applicability of a specific mathematical equation as
well as their closure techniques and numerical solution methods. The number and
characteristics of the soil layers should greatly affect the treatment pass
algorithms. Each layer can be treated as a different heterogeneous medium with
its own modeling equations. The junction of the layer description will be made
using FEA methodology. A new feature in this development is that the FEA is
used with the quite different governing equations. ......................

2. PROJECT FEASIBILITY MODELING
2.1 INTRODUCTION
We have been making emphasis on the real numerical
simulation of different scale problems of a Soil and Groundwater Contamination
System (SGCS) and model design during the Phase I. The codes have been
developed and the numerical simulation of the pore level model, regular network
flow model simulation, random sized 1D straight pore medium modeling,
non-Newtonian fluid (with power law viscosity) random distribution 1D pore
model numerical simulation, theoretical analysis of nonlinearities in the 2D
transport equations, the problem uncertainty preliminary analysis and the
overall software system preliminary design have been accomplished and presented
in the second part of the Phase I final report.
2.2 RESEARCH DATABASE DEVELOPMENT
Numerical modeling of turbulent and laminar flow in a slit with rough walls was performed
as a simulation procedure for the 2nd level modeling. The input data were
collected and classified in
the corresponding tables - Table 2.2.1
and Table 2.2.2 a,b. The tables were work out in Microsoft Excel,
like all the results of calculations, and stored in Microsoft Excel format as
the database.
The
data in the tables are
that necessary for understanding the process - physical parameters, boundary
conditions and slit's size (width). This data was not changed for all variants of calculation.
The numerical work
was conducted to determine
the influence of slit wall
roughness morphology on the transport characteristics. The kind
of roughness elements (obstacles), their
size and distance between them were the main parameters studied during the numerical
study. These three elements of the morphology and a code as
designator correspond to each separate
variant. Variant code was taken to be Tnhapm, where n
and m are integer; Tn is the type of obstacles, n = 1,5,8 were taken for current simulation
effort; ha , 0
< a < 1,
indicates the part of the slit width occupied with the obstacles: hr = ah; pm
signifies the value of obstacle height related to pitch:
p = mh.
The variant code given on the data chart and used in the graph
legends instead of the variant number allows one to show the
influence of morphology elements directly
on the graph.
The variant code key fields also serve as a key fields
in a database of the results.
.............................................
2.3 SINGLE PORE TRANSPORT MODELING
In this chapter, the results of broad scale numerical
simulation and code development for single pore transport system level are
presented.
2.3.1 INTENSE AND TURBULENT TRANSPORT IN ROUGH PORE.
A model
of transitional groundwater flow in a highly permeable horizontal
slit potentially consisting of young
carbonate or volcanic rock is presented for two-concentration solute
transport and two-temperature heat transport. The governing
equations given in Chapter 1.6 (1.6.3) - (1.6.8) were obtained by an advanced averaging
technique, developed and described by Travkin and Catton (1992a,
1993a,b). The elementary microvolume morphology considered is a slit with
highly rough walls. The objects
of current numerical modeling and analysis were regular arrangements of three-
and two-dimensional
discrete obstacles of
various types. The following varieties of roughness geometries were studied:
A. Two-dimensional geometries B. Three-dimensional round-shaped
obstacles (Fig.2.3.1-2.3.2)
obstacles (Fig.2.3.3)
-rectangular ribs (code T1) -
spheres (code T5)
-trapezoidal ribs (code T2) - cones (code T6)
-triangular
ribs (code T3) - cylinders
(code T7)
-semi-cylindrical
ribs (code T4) - half-spheres
(code T8)
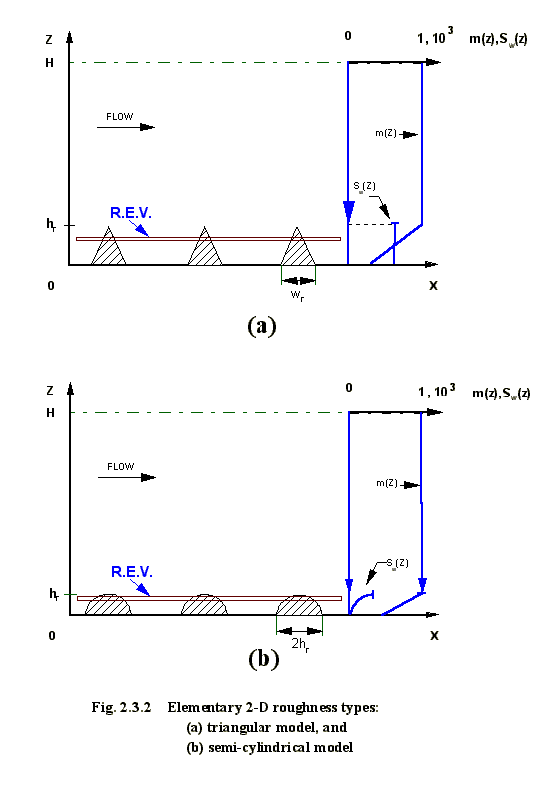
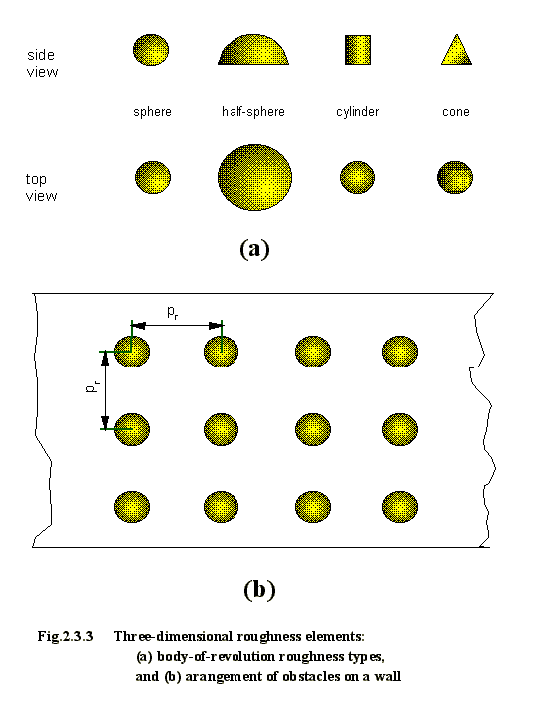
..................................................
The drag of the roughness elements on a rough wall
creates another component of
wall shear stress, in addition to the viscous stress and the
Reynolds stress. Similar to flow over a smooth wall, the flow can be considered
to be two-layered, with a sublayer that contains the roughness
elements and an outer layer where the shear
stress is affected by the turbulent viscosity. The system of roughnesses was
simulated as porous media (Catton, Travkin, 1992a). The objective of this work was to
study the influence of different
kinds of morphology on the local flow characteristics
( velocity profile, effective viscosity, laminar and turbulent Nusselt numbers), and on the mean characteristics, such as averaged
velocity, drag coefficient,
viscosity and Nusselt
number. Velocity and
viscosity were averaged along the slit
width. Drag coefficient and Nusselt
number, defined just
into the porous layer, along the
obstacle and equal to zero outside, were averaged across the
obstacles layer.
A
slit of half-width equal to
1 mm was taken for numerical modeling;
the solid phase was presented by rock
and the fluid phase by water.
All the
characteristics of the flow
were observed from the left boundary to a distance of 20
mm from the left boundary. Most numerical experiments and analysis were done for 3D half-spheres, 3D spheres and 2D
rectangular ribs. The height of the obstacles was varied from
0.1 to 0.9 of the slit width and
the distance between the obstacles was varied
from 0 to 4 obstacles in height. Width of the rectangular ribs was equal
to their height. The input data are presented in Table 2.2.1.
The results of the calculation are displayed as
charts for averaged characteristics and as graphs for local ones. The Reynolds number in
all variants .....................................
2.3.2 LAMINAR REGIME ROUGH PORE TRANSPORT
When
underground water flow and
contamination transport in porous media are studied, the main interest is the laminar flow regime
because this kind of flow is what most often takes place under natural conditions. The study
of laminar solute transport in a porous media at microscale could produce an
understanding of nature and a way
of determining the value
of hydrodynamic dispersion -
one of the principal factors in
the process of contamination transport
(Bochever and et al., 1979). As noted above, the model of porous media at
the 2D level was taken to be a slit with highly rough walls. The governing
equations for two-temperature (or two concentration) laminar flow
in a porous media, developed
in Chapter 1.6, are equations (
1.6.9) - (1.6.16). The boundary
conditions are given by equations (1.6.8).
The main difficulties in constructing a model of laminar flow
is determination of the value of
the drag coefficient - cd ,
which is necessary for closure of the model. Most investigations in this field have been focused on
turbulent flow ( Schlichting,
1979; and other numerous authors). The few works where the laminar flow in a
rough channel was investigated (Davis, 1993; Koplik
at al., 1993) did not give any recommendations about proper values of the drag
coefficient. In the first paper (
The objective of the present numerical simulation was to show the influence of roughness morphology from the 1st level on
laminar flow characteristics at the 2d level. Three kinds of obstacles were modeled - 2D rectangular, 3D half-spheres and 3D
spheres. (Fig.2.3.1 - 2.3.3).
Two series of computations were performed. For the first one, the obstacles were taken
to have height equal to 0.1, 0.5 and 0.9 of the slit half-width. The width of
the rectangular obstacles was equal to their height. Table 2.2.2a contains the input data for
these calculations. Three values
of the pitch
correspond to every obstacle height for
all three kinds of obstacles - in
total 27 variants were calculated.
...........................................
........................The results are of enough
interest to be studied
in more detail during
Phase II for code validation and the diversity they provide.
CONCLUSIONS
1) A computer code
for rough crack (or large pore) momentum and heat transport has been produced.
This code is capable of simulating highly intensive even turbulent transport
regimes in a pore or crack of 1 mm to 1 cm hydraulic diameter scale. The
results obtained to date are very encouraging. Transport processes in a rough
pore with different morphological types of roughness were simulated. Various
kind of tortuosity of a pore system are available for
modeling by assigning a tortuosity wave length, the
intermittency of the wave pack and the transport path wall roughness
characteristics. Accounting for tortuosity is another
example of a dual-scale transport subsystem in SGCS.
2) The effects of
different pore level blocking using regular pore wall roughness morphology
models were simulated. Numerical experiment results with pore wall roughnesses of various structure; 2D rectangular, cone and semicylinder ribs, 3D - semisphere,
cylinder, cone, and sphere blocking elements were carried out. These roughness
models are valid and used to get the results for momentum transport as well as
for heat and mass transport in a single pore.
3) The mass- and
heat transport characteristics on an interface surface including the roughness
elements were obtained. The more important of these data are being transferred
to a database on a PS and analyzed with the help of standard PC software;
namely Excel and Freelance Graphics.
4) A second code
for rough pore modeling of the laminar momentum transport regime has been
developed. The results of a numerical simulation were obtained and analyzed for
both regimes and will be as follows:
Turbulent flow.
5) The main impact
on flow characteristics is by height of the obstacle. The values of the pitch follows
and influence of the kind of
obstacle on velocity and viscosity is not as clear. 2D rectangular
obstacle have an obvious influence on the Nusselt
number and drag
coefficient because of the jump in the specific surface at the top of the
obstacle. This influence shown as for the
local, so for the averaged
characteristics.
6) For small obstacles
with height equal to 0.1 of the half-width of the slit or less, all
characteristics, except drag
coefficient, do not depend on the morphology.
For Nusselt number it is true
except at the top of 2D rectangular obstacles. For viscosity a difference
begins at hr =
0.5h and is clear shown for areas
near and higher on the obstacle. Nusselt
numbers depend mainly on the obstacles height for hr < 0.9h .
Laminar flow.
7) The three regimes of the flow
exist, depending on the distance between obstacles and their height.
8) The first regime - roughness does not
influence to the flow very much. It occurs when spherical obstacles are situated
at a distance more that their width and rectangular obstacles at the distance
more than twice their width, and when
their height is not too big.
9)
The second regime - dimensionless velocity increases in comparison with velocity in a
smooth slit, like flow in a narrowed slit and occurs when obstacles are too close to one another;
10) The third regime - the flow behaves like flow
in a porous medium when the obstacle height is large enough.
2.4 MICROSCALE
NETWORK MODELING
One
of the major elements of the present project is the development of real pore network models for
different scales. Effort has been concentrated advancing the theoretical basis
of network simulation. Early work on this topic focused on schematic simulation
of network morphological parameters and transport physics.
There
is a problem of how to relate porous medium morphology characteristics that can
and are being measured to transport equations and coefficients. Essential differences
exist in our approach (HSP-VAT) and the commonly used effective medium
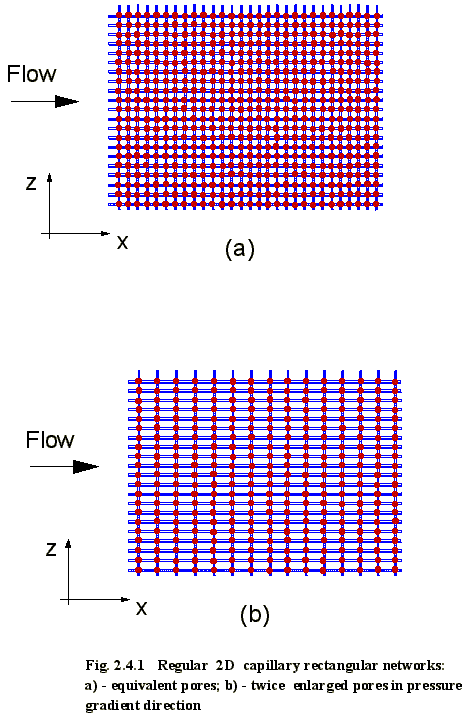
approximation (EMA) approach where the actual pore network is replaced by a
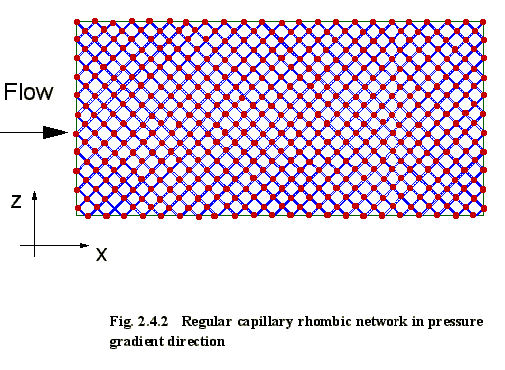
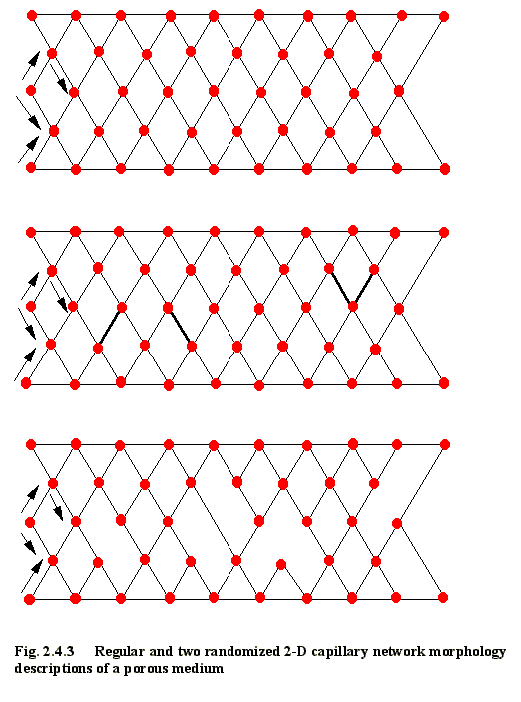
network with artificial uniform morphology, as shown on Figs. 2.4.1 and 2.4.2,
and effective properties, such as the effective diffusivity, Deff, or the effective reactivity, Reff. An important consideration, most often not
dealt with, is determining
which network morphology
properties can be assigned externally, or from an effective properties
point of view, which can be justified. The network characteristics should be
calculated where feasible to match the problem features, not just assigned.
......................................
...................................Further,
much of the previous research results were based on substitution of porous
medium properties and functions using artificial network simulation
capabilities without satisfying the initial equations. The concern here is that the physical
problem, which is simulated with the help of network modeling, must still be
modeled in such a way that its initial physical and mathematical statements are
properly treated. The development of models of irregular and random networks of
pores in the REV, with consequent substitution of closed morpho-convective
and morpho-diffusive terms into the transport
equations, was a part of the current research.
A
comprehensive approach has been initiated that consists of a properly
constructed scale network morphology and simulation of groundwater momentum,
heat and mass transport, including species, in a basic network of morphological
elements. For example, network bonds (pores) and nodes (junctions), as well as
transport modeling in advanced networks with random morphological
characteristics (Fig. 2.4.3 - 2.4.4) ....................................
CONCLUSIONS
1) Simulation of capillary networks consisting
of nodes (various junctions) and pores to model function fluctuations and to
use them in equations closure was accomplished. Two computer programs were produced. One
simulates very low momentum transport while the other focuses on the non-linear
analysis of a capillary network. This effort resulted in a different approach
for flow resistance calculations.
2) The development of a prototype network
momentum computer code has been completed and preliminary results have been
obtained. This is the initial step in modeling of a groundwater network at the
3d level. We plan to use these results in our implementation of the next level
of the averaged transport equations. Several network morphologies at millimeter
scale were studied by computer simulation.
2.5 STRAIGHT
PORE MORPHOLOGY MATHEMATICAL MODEL DEVELOPMENT
Admission
of specific types of medium irregularities or randomness requires the inclusion
of complicated terms in the governing equations. The governing equation for
steady, developed momentum transport in a spatial structure of straight
capillaries, which often finds usage as a canonical morphological model of
porous media, is as follows after the natural morphological simplification
of equation
(1.7.68):................................................
2.6 RANDOM
DISTRIBUTION PORE SIZE MORPHOLOGY
The
results of numerical simulation of specific morphology closure statements
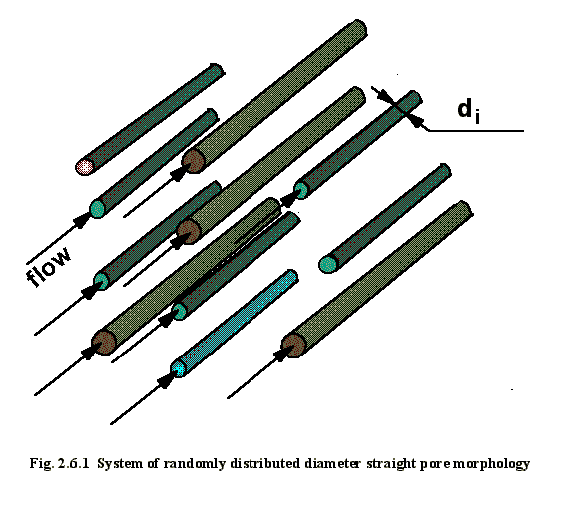
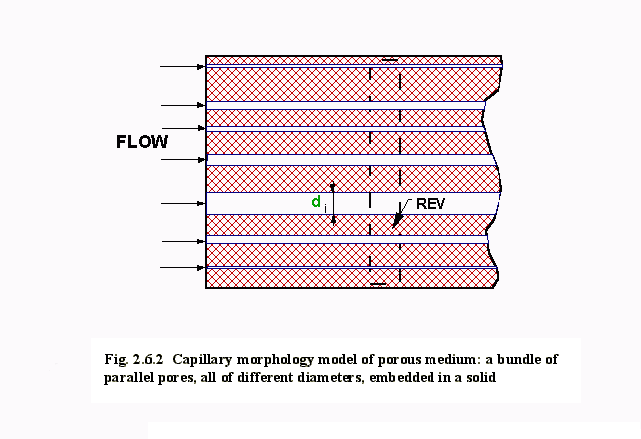
described in Chapter 2.5, for straight parallel pores with random distribution,
see Figs. 2.6.1 and 2.6.2. One of the primary goals of this simulation was to
obtain momentum transport results which are exact solutions and for which exact
averaging procedures could be accomplished for a broad spectrum of flow
regimes. Another goal was to obtain exact results for non-Newtonian fluid
motion in a porous medium. A non-Newtonian model of a power law fluid was
selected for simulation. To our knowledge, this is the first time these kinds
of modeling have been accomplished..............................
2.6.1 NEWTONIAN
GROUNDWATER VISCOSITY MODELING
The
distribution of pore radii was taken as uniform. The first series of calculation
was made for a diameter range of 0.0 to 0.003 m as well including fine pores
and pores with diameters of 0.001 m order of magnitude. Fine pores include
pores with diameters of 10-6 m and less. They were modeled for
different flow regimes in different pores and for various assigned pressure
drops. A laminar flow regime in each pore was achieved by choosing a low enough pressure drop.
Nevertheless, even for a uniform flow regime and uniform pore radius
distribution, outcome functions sometimes reflect an extreme shift toward the
left side of the result ranges - Figs. 2.6.3 through 2.6.7.
Drag
coefficient values are distributed over the seven orders of magnitude, while
the pore diameter extends only over the three orders of magnitude. In our earlier
research work, we developed and intensively tested a model and computer code
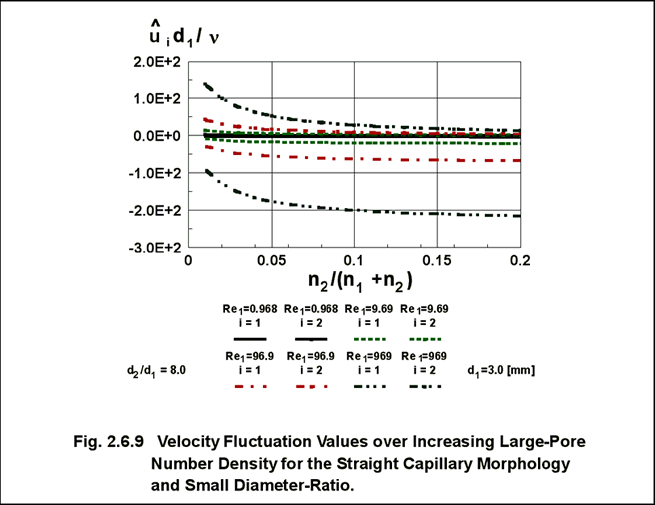
for the two different diameter arrays of straight capillaries, Fig. 2.6.8. This
study has shown some the interesting dependencies for function behavior as
shown in the Figs. 2.6.9 and 2.6.10. These results have been benchmark results
for comparison with the results of stochastic pore distribution analysis and
their verification. .........................
2.6.2 NON-NEWTONIAN
CONTAMINATED FLUID TRANSPORT
Modeling
and numerical simulation of porous media momentum transport with a
non-Newtonian fluid viscosity model was accomplished for groundwater flows. A
straight capillary morphology porous media model was used. A power law
non-Newtonian fluid dynamic viscosity in fully developed flow is (see, for
example, Savvas et al., 1994)
..............................................
CONCLUSIONS
1) A random pore diameter morphology model was
developed and implemented in a computer code. The objective of this modeling
was to determine the impact of a random pore distribution on averaged and
fluctuation values of momentum and heat transfer.
2) Exact modeling in each straight pore was
combined using theoretical closure analysis for a given morphology. Two kinds
of pore diameter distributions were used: 1) uniformly distributed diameters in
the range 0 to a few millimeters or few centimeters and 2) two-mode regularly
distributed pore diameters. This two distributions
resulted in dramatically different distributions of velocity, dispersion
coefficient and other characteristics.
3) An analysis of statistical data modeled on
exact solutions for assigned capillary morphology was provided. It showed the
tremendous importance of the lowest size pore distribution phenomena. It was
found that a negligible part of the overall momentum transport goes through the
smallest pores, yet the heat and mass transport through these pores is a large
fraction of the bulk transport due to their significant interface transport and
enhanced transport peculiarities in fine pores.
4)
The capability of some statistical data analysis software (namely the
"BESTFIT") demonstrates its lack of sensitivity and accuracy. There
is a need to develop more advanced statistical distribution analysis software.
5) A non-Newtonian fluid model has been
introduced for use with the specific capillary morphology that was coded.
Simulation results show the importance of non-Newtonian viscosity model
counting in the modeling of bulk and local transport characteristics.
2.7 THEORETICAL
ANALYSIS OF FLOW AND TWO-TEMPERATURE POROUS
MEDIUM MODELING
EQUATIONS
2.7.1 NONLINEAR
UNIFORM POROSITY EQUATIONS
The
work reported here is based on analysis of nonlinear model for two-temperature
heat and momentum turbulent transport in porous media recently proposed by Travkin & Catton (1992a,b; 1995c). The model
incorporates two new features: nonlinearity and nonuniformity
of the porosity. To establish the
importance of these effects, is first given to nonlinearity alone in Sections 2.7.1 , with both effects being considered in Section 2.7.2.
.....................................................
2.7.2 WEAKLY
NONLINEAR EQUATIONS FOR NONUNIFORM POROSITY
................................................
2.7.3 STRONG
NONLINEARITY AND SLOWLY
VARYING NONUNIFORMITY IN
POROSITY
To
determine the dominant nonlinearity in a slightly nonhomogeneous
porous media, the
multiple-scale method (Cole & Kevorkian, 1990; Nayfeh, 1975; Hinch, 1991) was
applied to the solutions found in Section 2.7.1. The change in porosity, p(z),
is assumed to be "slow" on the scale of a typical pore radius a, that
is ...............................
RESULTS AND CONCLUSIONS
1) Analysis of closed forms of the porous medium
transport equations developed in this work was accomplished. These equations
usually incorporate two features: nonlinearities of different kinds and nonuniformity of porosity. The closed form of the steady
state momentum equation in a porous channel was solved using a Weirstrass function with two invariants. The equation for
fluctuation energy was reduced to Abel's equation and expressed in terms of
elementary functions.
2) For relatively small nonlinearities,
expansion of the fluid momentum equation solution into a power series allowed
one to calculate the mutual influence of nonuniform
porosity and nonlinearity. The first terms in the expansion show the influence
of nonuniformity alone. For a regular porous
structure of spherical packing, the velocity function is expressed in terms of
modified Bessel functions. Analytical solutions and evaluation of some
simplified transport equations yielded the tools for analysis of the influence
of nonlinearity and nonuniformity of porosity.
3) Analysis of a nonlinear two-temperature and
momentum transport model features continues. The following important case have
been analyzed: the existence of simultaneous strong nonlinearity and
slowly varying nonuniformity of porosity. If the
change in porosity is characterized by a function f(x) with an assumed slow
change on the scale of a typical pore radius a, the rescaling of the coordinate
z is possible in a way that a new so-called slow variable Z= Lz is introduced.
4) Using the nonlinear solutions obtained and
reported previously, a Ginsburg-Landau equation for slowly varying modulation
of the equation solution was obtained. This equation is very well studied and
its solutions are expressed in terms of Hermitian
polynomials allowing one to get analytical solutions for studying many different morphologies.
2.8 UNCERTAINTY
ANALYSIS
An
estimation of the contaminant concentration at a receptor point in a porous
media includes uncertainties primarily because of the large temporal and
spatial scales involved in the transport processes. These uncertainties come
from a variety of sources. Completeness of the model assumptions and numerical
uncertainty in the parameter values are just some of the sources of
uncertainty.
The
parameter and modeling assumptions made in the transport model contribute to
uncertainties in the final results. An estimation of the weight of a particular
parameter or modeling assumption is very subjective. Such estimation, if
possible, should be based on sensitivity analysis, that is, on the
investigation of the impact of the parameter value or modeling assumption
changes on the final results. The uncertainties at this stage of understanding are
mostly not quantitative and can only be
described as subjective judgment. Unfortunately, there is
no consistent measures and procedures for model validation. Comparison of model
predictions with field or laboratory observations is, at present, the best way
of determining the model uncertainties.
Transport
equation coefficients are often burdened with uncertainty. In particular,
parameters which require indirect evaluation, such as permeability, may exhibit
uncertainty problems. In this context, uncertainty is relative to the true
value of the coefficient and not explicitly related to random porous medium
properties. It is the uncertainty due to errors in measurement and
interpretation.
There
are several types of uncertainty that arise in the phenomenological description
of physical
processes taking place during two_phase
(liquid-solid) contaminant transport in saturated soil systems. A typical type
of possible uncertainty is the uncertainty in the soil properties and model
parameters which are known with limited accuracy. Another type of uncertainty
that arises is an uncertainty associated with the type of model used to
describe the same phenomena. The first type of uncertainty is classified as
parameter uncertainty and the latter as modeling uncertainty. In addition,
uncertainties in the degree of completeness are sometimes identified as a special type of modeling
uncertainty. The evaluation of uncertainties embodied in the assessment of
contaminated groundwater transport processes involves: 1) estimation of uncertainties in the input
values; 2) propagation of input uncertainties through the whole analysis; and
3) combination of uncertainties in the output in order to obtain the
distribution of uncertainties in the final results.
There
is often a misconception regarding sensitivity and uncertainty analyses. A
sensitivity analysis is useful in estimating the effects of varying input
parameters, such as emission rates or dispersion coefficients, on the final
results. Uncertainty analysis allows one to compare the importance of the input
uncertainties with regard to their contributions to uncertainty in the outputs.
There is a variety of methods for uncertainty propagation and analysis. These
methods range from simple analytical approaches based on
A
number of methods are available for examining the effects of uncertainty in
modeling results. These include (Morgan
and Henrion, 1990),
! sensitivity analysis, for computing the effect of changes in
input values on the model output,
! uncertainty propagation, for calculating the uncertainty in
the model outputs induced by uncertainties in its inputs,
! uncertainty analysis, for comparing the importance of the
input uncertainties measured by their contribution to uncertainty in the final
outputs.
Numerous
methods for propagation and analysis of uncertainty have been developed, see Cox and Baybutt (1981) and Iman and
Helton (1988). They differ in their conceptual approach as well as in the
weight of information they propagate. There is no universal method that can be
applied to either problem.
A
screening level of uncertainty analysis was undertaken to assess the effects of
the uncertainties on the overall uncertainty of contaminant transport modeling.
This screening allow one to deal with uncertainties
when information is limited. The typical groundwater transport process taking
place in saturated soil systems involves a number of variables that may affect
the final result considerable.
In
general, there have been two main approaches to incorporating uncertainties
into groundwater transport models. The first is to include random parameters as
coefficients in the partial differential equations describing the transport
process. Then the equations, in their perturbated
form, are solved. This is a simplified approach which requires many additional
assumptions and first_order approximations. As a
result it could be a reduced accuracy.
A
second approach is based on
During
the first phase of this project the perturbation method, mostly due to lack of
good quality data, was used in uncertainty analysis.
The effort was limited to the parameter variables and did not include
correlations among them. The second phase of the project will utilize
Many
uncertainties were identified in the examination of two phase contaminant transport
simulation, but were not studied in detail. Some of these are discussed in the
other chapters of this report. In some cases, these topics were not pursued
because the time frame of this project did not allow modification of the code
to properly examine the impact of these uncertainties. Identification of the
most sensitive parameters in the equations of slow flow of contaminated
groundwater in the soil was made. A sensitivity analysis allowed us to find the
parameters with the highest impact on the final results. The transport equations
were treated parametrically and variables were assigned in the form of <u> + u';
where <u> is a mean value of the deterministic part, and u' is a random
part of the parameter. The parameters with influence less than (10% were used
as point values. For simplicity, only the x_direction
has been considered in this analysis.
The
most important variables, pertinent to the current project considerations, are
The
importance of geometrical dimensions of the pore and velocity of the
groundwater were investigated and results are presented in Chapter 2.6 for a
range of pore diameters from near 0 mm up to 6 mm. Liquid properties are needed
to evaluate the contaminant transport. The properties of interest are liquid
density, viscosity and surface tension. Uncertainty in the above properties is
caused mainly by the presence of dissolved or suspended materials. Water tends
to become heavily contaminated with suspended solids while interacting with a
saturated soil system. The surface tension of the liquid is considered to be
little affected by suspended solids since the soil particulates are not good
surface active agents. Inorganic solutes can either increase or decrease the
surface tension by approximately 8% according to CRC Handbook of Chemistry and
Physics. ...................................
RESULTS OF THE ANALYSIS
1) Identification of the most sensitive
parameters in the equations of slow flow of contaminated groundwater in the
soil were maid. A sensitivity analysis allowed us to
find the parameters with the highest impact on the final results.
The information obtain from this analysis allows one
to present the final results in the form of a mean value with upper and lower
bounds. Confirmatory calculations have been conducted on a few chosen
parameters.
Some of the conclusions are as follows:
1. Methodology
used at this stage is considered to be at a screening-level.
2. It is a
primary step in carrying out a full scale uncertainty analysis.
Hypercube
Sampling (LHS) is recommended.
4. One must
assign probability density functions to each uncertain value considered in the
modeling process.
5. Additional
research is needed to avoid ambiguities in choosing distributions for the probability
density functions.
2.9 SOFTWARE
SYSTEM DESIGN
The
overall design of the Model Software System (MSS) was conducted based on a
Top-Down design methodology and has evolved to comprise the following 5
functional subsystems, Fig 2.9.1:
...................................................
The
recommendations and conclusions resulting from the Phase I analysis and
modeling of groundwater transport phenomena are the following:
1) Basic subsurface soil
types and their physico-chemical characteristics
should be incorporated into a database to be used as a supplemental modeling
tool. Conceptual decision making procedures are being designed for each level
of the model hierarchy. We will assume for our purposes that soil
characteristics such as saturated hydraulic conductivity, clay content, bulk
density, available soil water content be admitted as classification criteria.
These and other parameters of the mining layer will serve as a characterization
vector in model selection and for model tuning procedures.
2) The modified structure of
contaminated water affects the filtration process and leads to inapplicability
of the Darcy law. Concerning the applicability of the different forms of the
governing equations in irregular curved pores, the first stage of the analysis
revealed that for pores with curvature, the governing equations have two
parameters which characterize the flow. The influence of curvature on flow is
evaluated in terms of these two parameters and in most cases this curvature
effect could be neglected. Further, the flow in a curved pore is much more
stable than in a straight pore.
3) Calculations of the flow
rates in our models must take into account the dependence of viscosity on
distance from the pore wall. As long as water boundary layers at nanoscale
remoteness from the solid phase are characterized by elevated viscosity, and do
not display a noticeable critical shear stress, they are important.
Measurements of water flow velocity in capillaries at a number of radii ( ranging from 5x10-2 :m to 1 :m ) have been used to determine the
4) As long as sorption from
contaminated groundwater to solid surfaces of soil and minerals plays a major role in the
distribution and fate of organic pollutants in the SGCS, work must be devoted
to developing reasonable phenomenological descriptions of adsorption using the
specifics of the current approach. The
specifics of the mineral and pollutant composition prescribe the possibility
for attaining a sorption equilibrium.
5) The type of sorption of
organic compounds depends greatly on the soil (mineral) organic matter content
and ion-exchange for some mineral compositions. Computation of equilibrium
compositions for simple aqueous solutions clearly demonstrate that describing
solid phase interfaces should be the goal of a separate software development
program, if known codes (for example, MINEQL, MINTEQ etc.) are found to be not
applicable.
6) The theory of volume
averaging (VAT) has been applied directly to the development of second and
third level transport equations. Spacial scales for
the channel's hydraulic diameter must be in the range from 10-9 m to
10-3 m if the flow regime studied is to be in the creeping or
laminar regimes.
7) The research goal was to
develop a dual-porosity "near" pore model and computer code featuring
a random and irregular interface surface (random surface morphology), permeable
solid phase model for transport of momentum, mass and heat with the correct
boundary conditions on the pore (crack) surface. This goal was achieved.
8) A computer code for rough
crack (or large pore) momentum and heat transport has been produced. This code
is capable of simulating highly intensive even turbulent transport regimes in a
pore or crack of 1 mm to 1 cm hydraulic diameter scale. The results obtained to
date are very encouraging. Transport processes in a rough pore with different
morphological types of roughness were simulated.
9) The effects of different
pore level blocking using regular pore wall roughness morphology models were
simulated. Numerical experiment results were obtained with pore wall roughnesses of various structure.
10) A second code for rough
pore modeling of the laminar momentum transport regime has been developed. The
results of a numerical simulation were obtained and analyzed for both regimes
and gave new insights. For example, for turbulent flow regime the main impact
on flow characteristics is by height of the obstacle. In Laminar flow the three regimes of the flow
exist, depending on the distance between obstacles and their height.
11) The development of a
prototype network momentum computer code has been completed and preliminary
results have been obtained. This is the initial step in modeling of a
groundwater network at the 3d level. We plan to use these results in our
implementation of the next level of the averaged transport equations. Several
network morphologies at millimeter scale were studied by computer simulation.
12) Simulation of capillary
networks consisting of nodes (various junctions) and pores to model function
fluctuations and to use them in closure equations was accomplished. Two computer programs
were produced. One simulates very low momentum transport while the other
focuses on the non-linear analysis of a capillary network. This effort resulted
in a different approach for flow resistance calculations.
13) A random pore diameter
morphology model was developed and implemented in a computer code. The
objective of this modeling was to determine the impact of a random pore
distribution on averaged and fluctuation values of momentum and heat transfer.
14) Exact modeling in each
of the large numbers of straight pore was combined using theoretical closure
analysis for a given morphology. Two kinds of pore diameter distributions were
used: 1) uniformly distributed diameters in the range 0 to a few millimeters or
few centimeters and 2) two-mode regularly distributed pore diameters. These two
distributions resulted in dramatically different distributions of velocity,
dispersion coefficient and other characteristics.
15) An analysis of
statistical data modeled on exact solutions for assigned capillary morphology
was provided. It showed the tremendous importance of the lowest size pore
distribution phenomena.
16) A non-Newtonian fluid
model has been introduced for use with the random capillary morphology that was
coded. Simulation results show the importance of non-Newtonian viscosity model
in the modeling of bulk and local transport characteristics.
17) Closed form analysis of
the porous medium transport equations developed in this work was accomplished.
These equations usually incorporate two features: nonlinearities of different
kinds and nonuniformity of porosity.
18) The
most sensitive parameters in the equations of slow flow of contaminated
groundwater in the soil were identified. A sensitivity analysis allowed us to
determine the parameters with the highest impact on the final results.
19) An overall design of the
Model Software System (MSS) was developed based on a Top-Down design
methodology.
4. REFERENCES
....................................