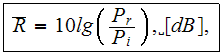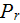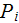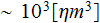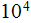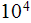Averaging, Scale Statements and Scaling Metrics in Homogeneous and Heterogeneous Electrodynamics
Having as an example of the two scale treatment in electrodynamics consider
here the photonic band-gap problem, which is often just the problem of EM
propagation in the two-phase porous media. Note, also that in one scale
electrodynamics this problem is often solved applying the "innocent" assumption
of the infinite domain used.
For the component one of the 2D two-phase (two different optical components)
dielectric medium with

 the homogeneous time-harmonic equation we can get for the photonic band-gap
study (see more in the "Optics" section - ) is
the homogeneous time-harmonic equation we can get for the photonic band-gap
study (see more in the "Optics" section - ) is
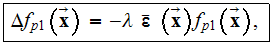 ______ (1)
where
______ (1)
where

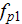 is the
is the

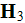 or
or

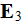 polarization
determined components of electric or magnetic fields and
polarization
determined components of electric or magnetic fields and

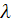 is the spectral parameter.
Meanwhile, the Upper scale HSP-VAT for the same phase component with the
constant coefficients is
is the spectral parameter.
Meanwhile, the Upper scale HSP-VAT for the same phase component with the
constant coefficients is
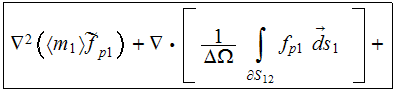
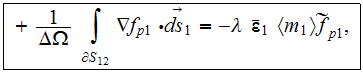 ______ (2)
______ (2)
Comparison of equation (1) and one of the simplest upper scale HSP-VAT photonic
medium equations (2) gives a ground for a number of observations which are
critical for understanding and proper application of HSP-VAT scaled
mathematical models in electrodynamics and linear optics. When one analyzes
(considers), for example, equations (1) and (2) it should be up front a clear
understanding of what does the global dependence

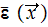 mean ?:
mean ?:
1) Is this the piece-wise constant in each of the phase function? Is the jump
condition present at the interface?
2) Is this the piece-wise constant function with the relatively smooth but
very thin transition layer of interface?
3) The most important question is - Are those interface physics phenomena so
important qualitatively or quantitatively that their influence should be found
in the governing modeling equations ?
The answers to these questions are laying mostly in the physics of another
(smaller) scale and they are not ready for pick-up in most of the problems.
Studies (Gratton et al., 1996; Travkin et al., 1995, 1998a, 1999a, 2000a,
etc.) concerning the thermal macroscale physics and fluid mechanics in
capillary and globular heterogeneous (porous) medium
morphologies demonstrated that even when interface
transport has no openly declared physical special features as, for example,
surficial transport - longitudinal diffusion or adsorption, etc., the input of
additional surficial and fluctuation terms in the upper scale HSP-VAT
equations solutions can be significant, reaching the same order of magnitude
in balance, as traditional diffusion, heat exchange or friction resistance
terms input.
That means
- the another non-traditional scaled physical effects are exist and we need to
take this into consideration when building the two (or more) scale physical
model, experiment, optimize the structure.
More importantly to have the lower scale physics of the interface included in
the upper scale governing equations when this physics is somehow different
from physics of upper scale. In electrodynamics those are, for example,
effects of polarization on interface surface, surficial longitudinal waves or
current, surface plasmons, etc.
There is the very interesting problem of coupling physics of reflection and
transmission of EM incidental wave based on the language of nanoscale surface
non-local electrodynamics with the continuum physics of upper scale HSP-VAT
description. This is rather natural task within the scaled HSP-VAT description
of transport in heterogeneous media.
Meanwhile, there is no other theory or approach which could include within
itself the governing equations formulations of the physical phenomena from
neighboring lower or upper scale description. We are not talking here about
source terms inclusion. The source term inclusion provided usually in the form
of some analytical formulae to describe an effect when there is the lack of
knowledge or resources, or no vital necessity in analyzing the coupled
phenomena of different scales.
The homogenization and fractal methods are inapplicable in most of the
situations. Fractal approach is not relevant to most of the morphologies, and
the fractal phenomena description is generally too morphological, lacking many
physical features presented - as, for example, descriptions in both phases, or
description of the phase interchange, etc.
The most sought after characteristics in heterogeneous media transport, which
are the effective transport coefficients can be correctly determined using the
conventional definition as for the effective conductivity, for example
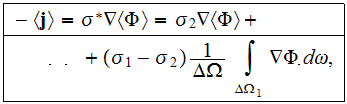 but only in the fraction of problems, even while employing the DMM-DNM exact
solution. The issue is that in majority of problems, as for inhomogeneous,
nonlinear coefficients, for example, and in many transient problems having the
two-field (EM) DMM-DNM exact solution is not enough to find effective
coefficients, because the formulation of correct formulae is beyond the
homogeneous methods tools.
but only in the fraction of problems, even while employing the DMM-DNM exact
solution. The issue is that in majority of problems, as for inhomogeneous,
nonlinear coefficients, for example, and in many transient problems having the
two-field (EM) DMM-DNM exact solution is not enough to find effective
coefficients, because the formulation of correct formulae is beyond the
homogeneous methods tools.
Thus,
returning to equations (1) and (2) it should be clear understanding that the
representative point (RP) of electric field component in (1) is the dot point
of approximate size

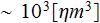 ,
which includes
,
which includes

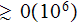 atoms. Then the reasonable representative elementary HSP-VAT volume (REV) at
the upper scale for the equation (2) can be about
atoms. Then the reasonable representative elementary HSP-VAT volume (REV) at
the upper scale for the equation (2) can be about

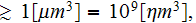 including within itself the thousands of lower scale RP volumes together with
their structural elements, etc.
including within itself the thousands of lower scale RP volumes together with
their structural elements, etc.
This REV volume would contain

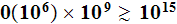 atoms or
atoms or

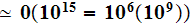 atoms, this is even for today's upper end high power supercomputers not a
solvable MD problem.
atoms, this is even for today's upper end high power supercomputers not a
solvable MD problem.
We need to understand that the HSP-VAT allows us to do this
calculation by now- at this time, not waiting more for unknown number of
years, and what is More Important, using this simulation scaling correctly.
Not just summarizing the box atoms movements.
And remember - this is not the MD box modeling. There is no actually a good
purpose to calculate such a grand volume of atoms - in any situation this
won't be a correct calculation - because this piece of matter already has
irregularities included. The REV at the said above scale

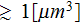 these irregularities includes. And again, the simple volume averaging of this
number of atoms features will not give correct answers if using the OG theorem
formulae.
these irregularities includes. And again, the simple volume averaging of this
number of atoms features will not give correct answers if using the OG theorem
formulae.
That means
also, that when one needs to consider the equation (1) then any single point
where it is valid is considered being or in one dielectric phase (for photonic
media), or in another phase, or at the interface, and the representative point
"size" of it (the volume ) is RP

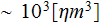 and this is the very generous size for homogeneous
matter
and this is the very generous size for homogeneous
matter
 The larger size RP might be inhomogeneous by nature of the material. It can
include, for example, molecular scale defects, shifts, etc. And strictly
speaking the smaller size is needed.
The larger size RP might be inhomogeneous by nature of the material. It can
include, for example, molecular scale defects, shifts, etc. And strictly
speaking the smaller size is needed.
Meanwhile, the probe size and the size of interest in
measurement of reflected and transmitted EM fields and energy are much bigger then
the size of the REV

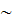

![$1[\mu m^{3}]$](/eldyn/pic/eldynscaling__21.gif) as we determined above. That means, the reflection coefficient for the
photonic (and for any microporous) medium volume or the transmission
coefficient are the averaged variables by definition
as we determined above. That means, the reflection coefficient for the
photonic (and for any microporous) medium volume or the transmission
coefficient are the averaged variables by definition
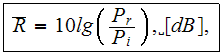
where

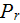 is the reflected power and
is the reflected power and

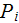 is the incident EM power. That means that the interesting in application and
the measured variables as EM wave propagated through the medium volume or
surface are averaged over the volume even larger then the
REV's size we accepted as resonable. Equation (1) does
not match to this scale range. Solving equation (1) in a two-phase medium
means that the variable corresponds to the field's point averaged over the
volume of
RP
is the incident EM power. That means that the interesting in application and
the measured variables as EM wave propagated through the medium volume or
surface are averaged over the volume even larger then the
REV's size we accepted as resonable. Equation (1) does
not match to this scale range. Solving equation (1) in a two-phase medium
means that the variable corresponds to the field's point averaged over the
volume of
RP
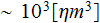 or less. And just having these fields averaged over the larger volume to look
for corresponding size volumes in modeling and in experiment is not sufficient
enough for few reasons, some of them we are just discussing
above, in this section on HtElectrodynamics, in a few other places in this website, and in
or less. And just having these fields averaged over the larger volume to look
for corresponding size volumes in modeling and in experiment is not sufficient
enough for few reasons, some of them we are just discussing
above, in this section on HtElectrodynamics, in a few other places in this website, and in
see also in (Travkin and Catton, 1998a,2001; Travkin et al., 1999, 2000a,b).
Still, the main reason, why equation (2) together with the lower level
micromodel (1) is more correct tool to model the heterogeneous medium EM
propagation, is because it has the mechanisms (additional terms) which clear
role is to connect physics of lower scale transport, often different from
the upper scale, and morphology of the two-phase (or more) medium to its bulk
effective properties and upper scale fields.
It is essential to take into consideration qualitative transformation of
homogeneous conventional formulation EM wave propagation problem to
heterogeneous scaled (at least on two scales) problem as soon as the numerous
structural objects which separate the phases are introduced to the medium for
any good reason.
The processes of EM fields propagation at the lower scale - inside, around and
through a single separate element of two-phase medium as layer, globular
inclusion, void gap, etc., are not self-sufficient for describing or
controlling the characteristics of the medium.
On the other hand, the formulation of the EM wave propagation problem as the
task for one phase field equations, or even as for two-phase homogeneous
medium does not characterize or connect the local (lower scale) transport
characteristics directly to the performance of the medium or device, e.g. to
the upper scale. It does not explain also - how to improve the performance
features of heterogeneous device or optimize some of them.
These ideas can be demonstrated using the example of
a fiber Bragg grating, when more than

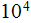 gratings along of the optical fiber can be used. This great number of
structural elements - as different refractive index gratings in the fiber
core, requires the evaluation of reflection coefficient locally in each
grating. Meanwhile, more important is the overall reflectance - the
reflectance of these
gratings along of the optical fiber can be used. This great number of
structural elements - as different refractive index gratings in the fiber
core, requires the evaluation of reflection coefficient locally in each
grating. Meanwhile, more important is the overall reflectance - the
reflectance of these

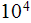 layers as a medium, which is the pure larger scale physical characteristic.
layers as a medium, which is the pure larger scale physical characteristic.
Formulation of this problem using the 2 scale two-phase HSP-VAT equations (2)
together with the lower scale (1) includes into analysis the interface
electric field exchange rate between the phases, effects of irregularities (as
Gaussian distribution) in gratings itself, etc. Using the only equation (1)
for that purpose ignores interface fields effects (even for constant phase
coefficients) and does the reflectance rate evaluation incomplete. It hides
also the hard task of coupling the grating performance to the phenomena of
temperature dependency, which became the standard problem in heterogeneous
thermophysics (Travkin and Catton, 1998a; 2001).


 the homogeneous time-harmonic equation we can get for the photonic band-gap
study (see more in the "Optics" section - ) is
the homogeneous time-harmonic equation we can get for the photonic band-gap
study (see more in the "Optics" section - ) is
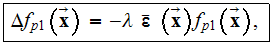 ______ (1)
______ (1)
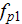 is the
is the

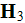 or
or

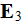 polarization
determined components of electric or magnetic fields and
polarization
determined components of electric or magnetic fields and

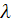 is the spectral parameter.
Meanwhile, the Upper scale HSP-VAT for the same phase component with the
constant coefficients is
is the spectral parameter.
Meanwhile, the Upper scale HSP-VAT for the same phase component with the
constant coefficients is
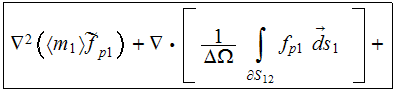
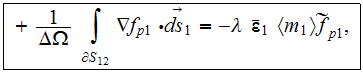 ______ (2)
______ (2)
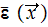 mean ?:
mean ?:
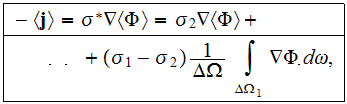

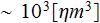 ,
which includes
,
which includes

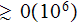 atoms. Then the reasonable representative elementary HSP-VAT volume (REV) at
the upper scale for the equation (2) can be about
atoms. Then the reasonable representative elementary HSP-VAT volume (REV) at
the upper scale for the equation (2) can be about

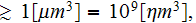 including within itself the thousands of lower scale RP volumes together with
their structural elements, etc.
including within itself the thousands of lower scale RP volumes together with
their structural elements, etc. 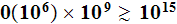
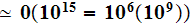
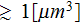
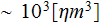

![$1[\mu m^{3}]$](/eldyn/pic/eldynscaling__21.gif)