Students should be aware and have to give some thoughts regarding their undergraduate, graduate, and post-doctoral education based on the information - which is the University and Institution able to teach, practice, and develop applications based on the correct fundamental courses for Heterogeneous Matters, Media, Devices and True Multiscaling in the following fundamental disciplines:
1) Particle Physics;
2) Particle Physics 2;
3) Nuclear Physics Structured;
4 Electrodynamics;
5) Electrodynamics 2;
6) Atomic Physics;
7) Ferromagnetism;
8) Continuum Mechanics;
9) Heat Transfer;
10) Mass Transfer;
11) Thermal Physics;
12) Fluid Mechanics ;
13) Electrostatics ;
14) Acoustics;
15) Environmental Engineering;
16) Air Pollution (Urban and Modeling);
17) Agro-Meteorology;
18) Nanotechnologies;
19) Optics;
20) Materials Science;
21) Semiconductors;
22) Superconductivity;
23) Composite Engineering;
24) Experimental Science for Heterogeneous Matter;
25) Optimization in Heterogeneous Media;
26) Biology 3P (Polyscale-Polyphase-Polyphysics);
27) Biology Multiscale Applications;
28) Biotech many Fields;
29) Health Sciences; etc., etc.
In all these courses should be included and Taught the
following topics or some parts of those
and of the technical problems of the Two-scale (at least) nature:
1) Elements of Heterogeneous Physics and Mathematics;
2) Elements of 2P Particle Physics;
3) What are the Nuclei in Elements;
4) What is the Electromagnetism of Atoms and Particles;
5) What is the Interaction and Aether in Physics;
6) Conductivity, Diffusivity, Electrical Permittivity of the Two Scale Media with Globular Inclusions, for Spheres This Problem Have Been Solved Exactly. Lecturers Must Know or at Least be Able to Describe and Discuss How This Problem Was Solved, and What are Implications.
7) Conductivity, Diffusivity, Electrical Permittivity of the Two Scale Media with Straight Rods (Bars) Second Phase of Inclusions. For Morphologies with Dilute Random or Functionally Dependent Diameters This Problem Have Been Solved Exactly.
8) Conductivity, Diffusivity, Electrical Permittivity of the Two Scale Media with Two Phase Layered Morphology. For Morphologies with Linear Statements This Problem Have Been Solved Exactly.
9) Momentum transport, Conductivity, Diffusivity, Electrical Permittivity of the Two Scale Media with Straight Pores of the Second Phase. Flow regimes might be of three types (laminar, creeping, and turbulent), that other methods can not apprehend. For Morphologies with Dilute Random or Functionally Dependent Diameters these problems have been solved.
10) Momentum transport, Conductivity, Diffusivity, Electrical Permittivity of the Two Scale Media with Straight Slits of the Second Phase. Flow regimes might be of three types (laminar, creeping, and turbulent), that other methods can not apprehend.
11) Fundamentals of Experimental Science for Heterogeneous Media and Devices.
12) Few Two-scale problems in Wave Mechanics - as in Acoustics, Electrodynamics, Elasticity. Few of them have been solved also exactly on both scales.
There is the great need to introduce this teaching first of all in the areas (professions) of nanotechs, medicine and life sciences, biotechs, and energy related technologies.
Why "should be taught these problems" ?
Simply because these are the basic principal classical problems usually taught in any coursework set that necessary for disciplines in technical, biotech and physical sciences specialties and the only known today Scaled, Hierarchical problems solved completely on both scale spaces, as well as the only known experiences with experimental techniques developed for scaled, heterogeneous devices two-scale experiments.
The methods, "theories" of other nature taught in the Universities mostly are simply
imitating the Multiscaling as a methodology, that's it.
Professors just verbally combine the
descriptions of different scale problems in physics, chemistry, biology and
telling the students - That's what you need to know and remember.
Couple of coefficients and you've got the "mathematical"
(but not a physical connection). It hardly reflects
the real physical dependencies in heterogeneous, scaled media and the tools in
need to model those.
For example, which is taken from the widely used undergraduate textbook on physics by Halliday et al. (2005) (textbook used and for biology students teaching), we can find in it the basic general rule
for the heat (mass) transfer through the multilayer wall - "Conduction Through a Composite Slab...." in p. 494 as the formula (18-37)
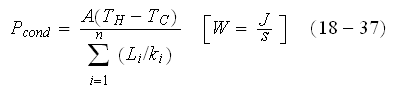
which is for unit surface

![$A=1[m^{2}]$](/edu/pic/right1__2.gif) in SI units can be presented as
in SI units can be presented as
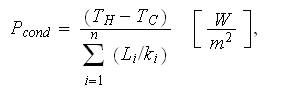
with the effective bulk medium coefficient of conductivity
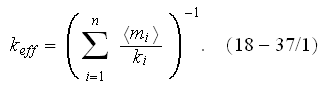

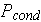 is the heat flux through the multilayer wall with fixed external surfaces
temperatures
is the heat flux through the multilayer wall with fixed external surfaces
temperatures

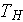 - the hot wall's surface and
- the hot wall's surface and

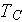 is the cold one, and
is the cold one, and

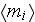 volume fraction of the i-th phase..
volume fraction of the i-th phase..
Authors of this example problem - which is the Two-scale problem, do not tell
the students that the formula

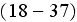 hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
1) that this is the two-scale
actually problem;
2) the Upper (the second) scale solutions are not achievable in brackets of
homogeneous physics. There are no definitions and mathematics (at least
correct ones) for that in homogeneous physics;
3) the steady-state mean heat flux and the effective conductivity coefficient
and of the transient problem ones are different by their definitions and
scaled mathematics involved, not by only fact that those
problems are different by time derivative and temperature depending on time;
4) the dependencies outlined in homogeneous physics solutions are incorrect
if being applied with the exact fields for the lower scale solutions as, for
example, the homogeneous formula gives the averaged difference temperatures
(averaged gradients) that are not equal to the difference (gradient) of
averaged temperatures
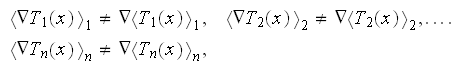
in spite that in homogeneous
physics they should be equal (here

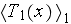 is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
Also, there is inequality one scale homogeneous physics can not explain
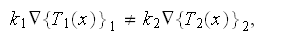
in spite that the homogeneous
thermal physics formula

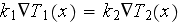 is correct (here
is correct (here

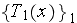 is the intrinsic phase averaged temperature,
is the intrinsic phase averaged temperature,

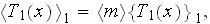 and
and

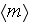 is the phase fraction).
is the phase fraction).
5) that for the linear problem there are the two physical mechanisms
involved in field's transport - 1) is the INTRAPHASE, in each phase transport;
and 2) is the INTERFACE transport each with their respective phase effective
coefficients. These transport means and phase effective coefficients are not
known in the one-scale homogeneous physics transport;
6) they don't tell the students that with this formula the transient problem
can not be solved;
7) that there is no solution for this problem of mean heat flux (heat rate)
in the transient formulated problem. The solution is achievable only via the
two-scale physical and mathematical statement.
8) the formulae (18-37) and

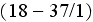 are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;
are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;
9) it might be impossible to design the optimal heat transfer or heat
protection multilayer coating while study only the one scale Homogeneous
statements. There is no one optimally designed yet - and that is the result of
the more than hundred years effort!? That is why it can be stated the optimal
design is unachievable when the one-scale thermal physics theory used.
Halliday, D., Resnick, R., and Walker, J., Fundamentals of Physics,
7th Ed., J. Wiley & Sons Int., (2005)
In various pages of this and other our sites spread multiple examples of such "teaching".
We start explaining and talking on this in -
Are there any other Methods and Theories available? http://travkin-hspt.com/fundament/04.htm
Even if lecturers, professors don't know how these solutions
were obtained and What is the HSP-VAT at all. Nevertheless, to be honest
with students they need to tell to students that this is it.
This kind of knowledge and solutions exist and this knowledge should be taught
to students if Universities (or any other educational Institution) adhere
to their policies of "state of the art" education.
This will be an advanced education for many fields that
Universities are struggling to add the specialties for and stay in the markets.
We can estimate some of educational Institutions, Universities
and give a researched summary on their abilities to teach or even to simply
concern the subjects of Scaling, Multiscaling, etc. etc. physics' content
and advancements.
We paid extraordinary attention to lecturing in our courses on the few scaled problems that were solved even exactly some years ago, actually from 94-95.
These two scale connected solutions, the solutions that explain hidden in textbooks incorrectness's and
inconsistencies - are supposed to overturn the many physical disciplines lecture courses. The main features of these solutions and
consequences are known since 1994-95. Through the years I also disseminated them to many professionals lecturing
in the universities, and particularly in fields demanding already for many years the usage of words - "local," "nonlocal," "heterogeneous," "multiscale,"
"averaged," "two scale," etc.
The content of this course below is by no means follows the usual university traditional teaching of the multi-phase transport and
processes in technologies and/or physics, and presenting them as they are like the one scale and GO theorem based disciplines.
On the other hand, this course and others portrayed in this website
are not quite similar to some courses with elements of linear and half-linear
HSP-VAT taught in few US universities,
because we had taken the basis for them as rendered with critical features
and detail in
Fundamentals of Hierarchical Scaled Description
in Physics and Technologies
That is why the outcomes and much of teaching materials and results and problems, are different in many parts and instances.
Course Outline:
(might be of undergraduate level):
Elements of Heterogeneous Media Transport - Local, Non-Local and Multiscale Theories
Instructor: Travkin, V.S.
http://travkin-hspt.com
Objectives of the Course:
The objective of this course is to provide the students with elements of transport of energy, mass and momentum in heterogeneous systems - based on hierarchical multiscale phenomena description theory (Hierarchical Scaled Physics Volume Averaging Theory - HSP-VAT). At present time the HSP-VAT is the only theory which suggests the correct physical and mathematical description and connection of processes on different scales of hierarchical media, materials, and/or fields.
Tentative outline:
First starting with the review of theories used for the description and problem statements in multiphase flow and heat and mass transport the course content will guide students through the basic physics and mathematics of collective phenomena. Among other major topics that will be covered are the heat transport in heterogeneous media such as composites, in addition to topics concerning experiments in heterogeneous media.
The basics of the multiscale field phenomenological and stochastic transport governing equations will be described and their application to thermal physics and fluid mechanics will be emphasized while comparing with known conventional problem formulations and mathematical statements. The pure analysis of classical problems of momentum and heat transport in heterogeneous media will be demonstrated with the hands on participation of students in various methodologies.
The major engineering issues of estimation of effective characteristics and coefficients will be emphasized in the course with applications in thermal science. Specific topics include effective conductivity coefficients, heat exchanger modeling methodologies and design, porous media fluid flow, permeability and flow regimes, experiments over composites and their data reduction.
Required Textbooks: none
Required Lecture Notes, Texts: few printed papers by Travkin, V.S. and
1. Travkin, V. S., "Particle Physics - Heterogeneous
Polyscale Collectively Interactive,"
2. Travkin, V. S., "Electrodynamics 2 - Elements 3P (Polyphase-Polyscale-Polyphysics),"
3. Travkin, V. S. and Bolotina, N.N., "Quantum Chemistry, Physical Chemistry, Molecular
Dynamics Simulation, DFT (Density Functional Theory), and Coarse-Graining Techniques
Applied in Structural, Cellular Biology, Polymer Science and Implication for
Scaleportation," Journal of Alternative Energy and Ecology, No. 2, pp. 58-75, (2011a)
4. Travkin, V.S. and Catton, I., Transport Phenomena in Heterogeneous Media
Based on Volume Averaging Theory, in Advances in Heat Transfer, New York,
Academic Press, Vol. 34., pp.1-144, (2001)
Recommended Textbooks:
Kaviany, M., Principles of Heat Transfer in Porous Media, 2nd. edition,
Springer, (1995).
Slattery, J.C., Momentum, Energy and Mass Transfer in Continua, Krieger,
Malabar, (1980).
Whitaker, S., "Volume Averaging of Transport Equations", Chap. 1, in
Fluid Transport in Porous Media, Computational Mechanics Publications, Southampton, UK, (1997).
In Russian
���� ������ :
(4-� � 5-� ����� �������)
( � ������ ���������� ��� ��������� 3-�� ���� ��������, ���� ����� ������������� � ��������)
�������� ���������� � ������������
������ - ���������, ����������� � ��������������� ������
������: T������, �.�.
http://travkin-hspt.com
���� �����:
���� ����� ����� ������� ��������� ��������� ������ � �������� ������������ ��������� ��� �������� �������, ����� � ���������� �������� � ������������ ������ - ������������ �� ������ �������� �������������, ��������������� ������� (���������� ������ ���������� - ���). � ��������� ����� ��� ������������ ������ ������� ���������� ���������� ���������� � �������������� �������� � ����������� ��������� �� ������ ��������� ��� �������� �������� ������� � ���������� � �����.
���������� �����:
� ������ ����� ����� �������� ����������� ��������� � �������� �������� � ��������������� �������������� ����������� ����� ��� ������� � ����� � �����������. ����� ������� ����� ����� ����������� � ���������� ���� � ���� (�� ������� ����) ��������� �������� ��� ������������ � ������������� ����. � ���� ������ �������� �������� ���������� ������� � ��������� ������ ����� ���������� �������������� �������� ���������������� � �������� � ������������ ������, ����������. ����� ������������������ ������ ���������� �������������� � �������������� ���������� ������������� ��� ����������� ������������� ���������������� � ������������� ������������ � ����������.
������ ��������������� ������� ������ � ������������������� � ��������������� ���������� ����������� �������������� ������ � �� ������������, �������� � ��������, ���������������� � �������� �������� � ����. ��������� ���������� ������� ���������� ���� ��������������� ������� ������ ��������� � ���� ����� ������. ��������������� �������� ��� ��������� � �������������� ������� ��������� � ���������� ��� ��������� �������������� ������� � �������������� ������������� � ������������ ���������� �������.
������ ������ ������������ ������� ��� ��������, ���������������� � ���������� �������� � ������������ � �������� ������ ����� ����������������� � ������������ �������� ���������, � �������������� ������� ������������ � ������ � � �����������.
�������� ��������������� ������� ��������� � �������� ����������� ������������� � ������������� ����� �������� � ����� � ���������� � ��������, ��������������, ����������� ��������������. ����� ���������� ��� ����� ����������� �������� ����������� ������������� �������� � ���������������� ��� ��������������, ����������� ������������� � ������� ��������������� ��� ���������������, ������� � �������� ������ ��������, ����������������� ������ � ������� ����������, ������ ����������������� ������ ����������� � ���������������.
����� ������� �������� � ����� ����� ������� ������ �������� ����������� �������������� ��������� ���������� � �������� � ��������� ����� �����. � ��� ����� �������� ����������� ������������� � ���������� ������������ ����������, ������� �������� � ��������� ����������� ����������� �������� ����.
��������� ��������: ���
��������� ������� ���������: ��������� ������ ��������, �.�.
and
Travkin, V.S. and Catton, I., Chap. 1, "TRANSPORT PHENOMENA IN HETEROGENEOUS MEDIA BASED ON VOLUME AVERAGING THEORY", in Advances in Heat Transfer, Vol. 34, pp.1-144, (2001).
������������� ��������:
Kaviany, M., Principles of Heat Transfer in Porous Media, 2nd. edition, Springer, (1995).
Slattery, J.C., Momentum, Energy and Mass Transfer in Continua, Krieger, Malabar, (1980).
Whitaker, S., "Volume Averaging of Transport Equations", Chap. 1, in Fluid Transport in Porous Media, Computational Mechanics Publications, Southampton, UK, (1997).
Copyright © 2001...Thursday, 03-Jul-2025 09:06:53 GMT V.S.Travkin, Hierarchical Scaled Physics and Technologies™
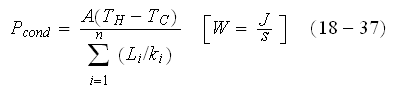

![$A=1[m^{2}]$](/edu/pic/right1__2.gif) in SI units can be presented as
in SI units can be presented as
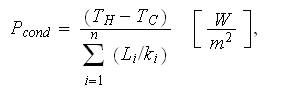
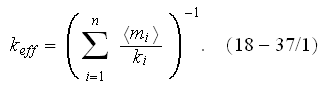

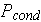 is the heat flux through the multilayer wall with fixed external surfaces
temperatures
is the heat flux through the multilayer wall with fixed external surfaces
temperatures

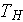 - the hot wall's surface and
- the hot wall's surface and

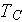 is the cold one, and
is the cold one, and

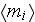 volume fraction of the i-th phase..
volume fraction of the i-th phase..

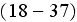 hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
hides the insufficiencies in the solution for mean heat flux (heat rate), for
example, as following:
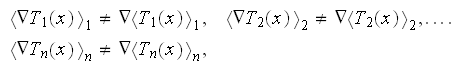

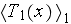 is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
is the phase averaged temperature). Why is that? There is no correct answer in
the homogeneous thermal physics for that.
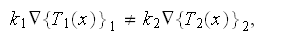

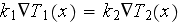 is correct (here
is correct (here

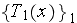 is the intrinsic phase averaged temperature,
is the intrinsic phase averaged temperature,

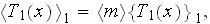 and
and

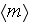 is the phase fraction).
is the phase fraction).

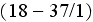 are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;
are invalid for transient heat transfer, for example, when one of the boundary
temperatures is changing during the time period. In spite that in this case
the difference in temperatures is still known, the heat rate ( mean heat flux)
can not be found via this formula and/or this method;