Composite Coating EM Reflection - Two and more Scales
We consider the incidence of the TE type (s-polarized) wave

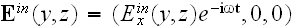 from the upper half-space
from the upper half-space

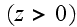 with the dielectric permittivity
with the dielectric permittivity

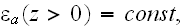 onto the lower subspace
onto the lower subspace

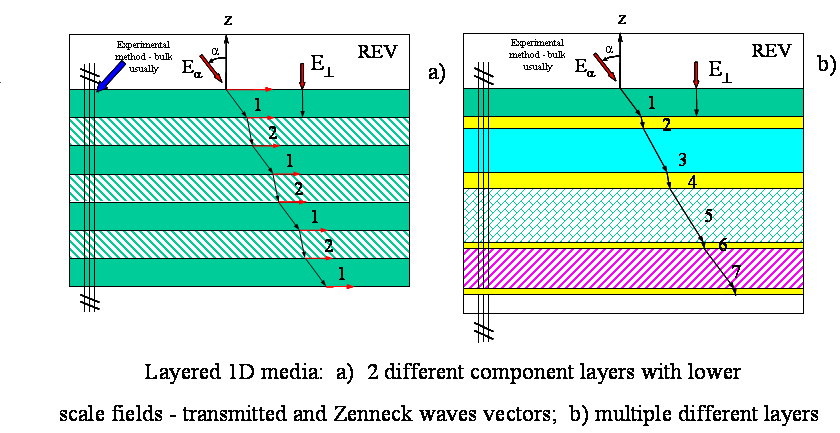
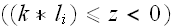 with the heterogeneous medium of 100 or 200 or even bigger number (600) of
layers, consisting of homogeneous, with constant coefficients layers of two
kinds, or inhomogeneous layers of two kinds when each layer of each kind has
the nonlinear dependency of material's electric properties.
with the heterogeneous medium of 100 or 200 or even bigger number (600) of
layers, consisting of homogeneous, with constant coefficients layers of two
kinds, or inhomogeneous layers of two kinds when each layer of each kind has
the nonlinear dependency of material's electric properties.
The system of

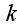 layers: with
layers: with

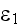

![$[\frac{F}{m}]$](CompositeCoatingEMreflection___7.gif) - dielectric permittivity of the odd layers,
- dielectric permittivity of the odd layers,

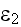

![$[\frac{F}{m}]$](CompositeCoatingEMreflection___9.gif) - dielectric permittivity of the even layers;
- dielectric permittivity of the even layers;

![$l_{i}[m]$](CompositeCoatingEMreflection___10.gif) - thickness of i-th layer;
- thickness of i-th layer;

![$\varsigma _{i}[m]$](CompositeCoatingEMreflection___11.gif) - coordinate of the upper boundary of the
- coordinate of the upper boundary of the

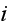 -th
layer;
-th
layer;

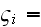

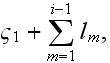 where
where

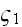 is
the layers pack's upper boundary z-coordinate.
is
the layers pack's upper boundary z-coordinate.
The statement with nonlinear properties has the much more complicated lower and Upper scale governing equations.
On the lower physical scale we have to use the Helmholtz equations

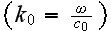 for the upper half-space region
for the upper half-space region
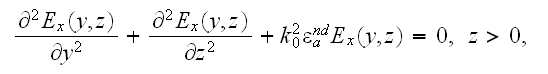
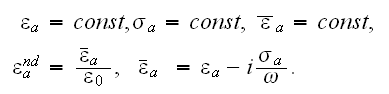 where
where

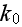 - the wave vector of the incident wave.
- the wave vector of the incident wave.
For the lower region with the superlattice the lower scale medium for each layer of kind 1 or 2 we can write:
1) First period - two layers -
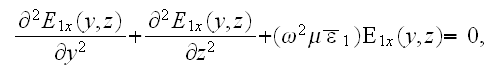
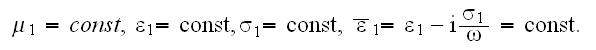
and
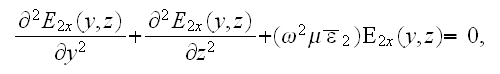
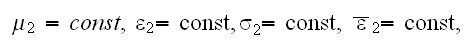
with the conjugate boundary conditions of the IV-th kind BC's as like in thermophysics. The two fields are having in the interface surface the BC's, for example, when the phase 1 contacts with the phase 2, then for the tangential components of the electric field should be
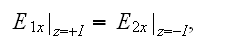
while the second BC appears from the condition for magnetic fields due to Amper's law
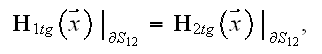
which implicates that
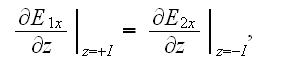 where the subscript
where the subscript

 means - the interface.
means - the interface.
For the 2D case we have, for example, the TE polarized in

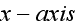

 direction
direction

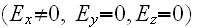 -
-
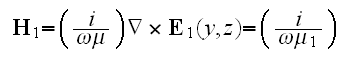
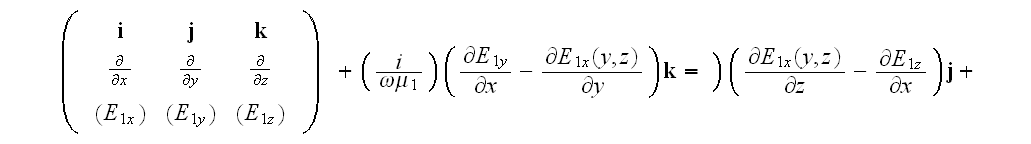
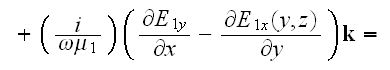
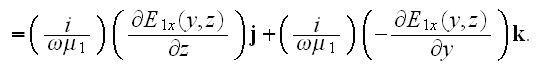
So, anyway the tangential component

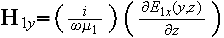 will
lay on the interface surface and the second BC will be the same.
will
lay on the interface surface and the second BC will be the same.
While for the bottom interface surface

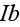 of the 2 layers period we have the BC's
of the 2 layers period we have the BC's
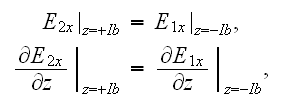
connecting fields to the following period. And for the all other periods the same mathematical statements occur.
The Upper Scale VAT Governing Equations
In linear case, when conductivity coefficient

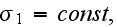 then the VAT equation in phase one simplifies to
then the VAT equation in phase one simplifies to
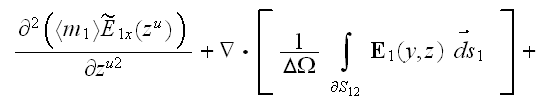
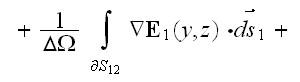
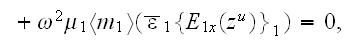
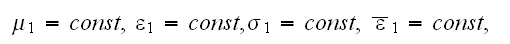
when we also have from the lower scale

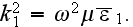
In the phase two the Upper scale governing equation is
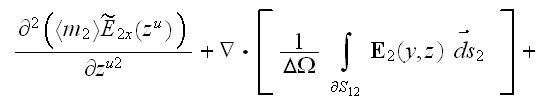
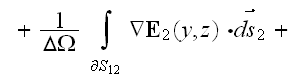
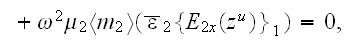
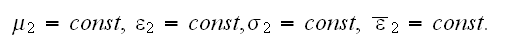
We provided the few situation solutions for this two-scale problem in the subsection -
"Electodynamics/Two Scale EM Wave Propagation in
Superlattices - 1D Photonic Crystals" -
http://travkin-hspt.com/eldyn/
and in another subsection -
"Optics/Photonic Crystals and Their Modeling" -
http://travkin-hspt.com/optics/....
Here we are interested in formulation of the definitions for the Two-scale properties for this problem. As usual, the one scale properties while often written as for local, point specific homogeneous one scale statement, in reality being implied as for the volumetric, averaged definitions for fields or their derivatives.